Graph Algorithms Introduction Terminology V E directed adjacent

Graph Algorithms

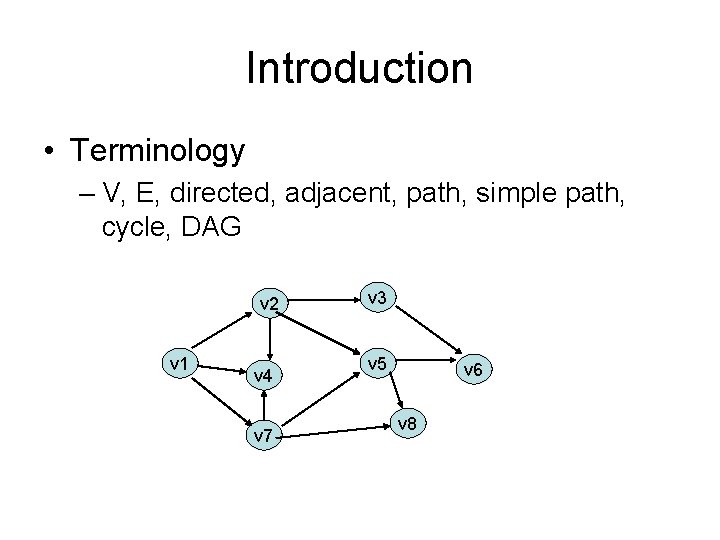
Introduction • Terminology – V, E, directed, adjacent, path, simple path, cycle, DAG v 2 v 1 v 4 v 7 v 3 v 5 v 6 v 8

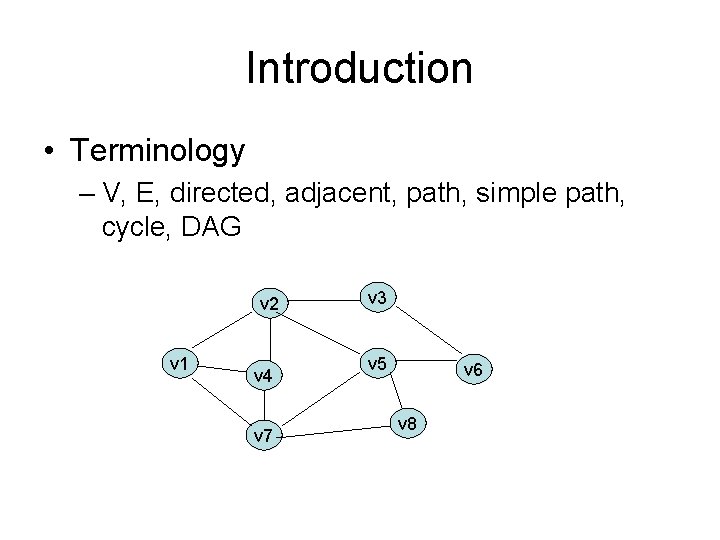
Introduction • Terminology – V, E, directed, adjacent, path, simple path, cycle, DAG v 2 v 1 v 4 v 7 v 3 v 5 v 6 v 8

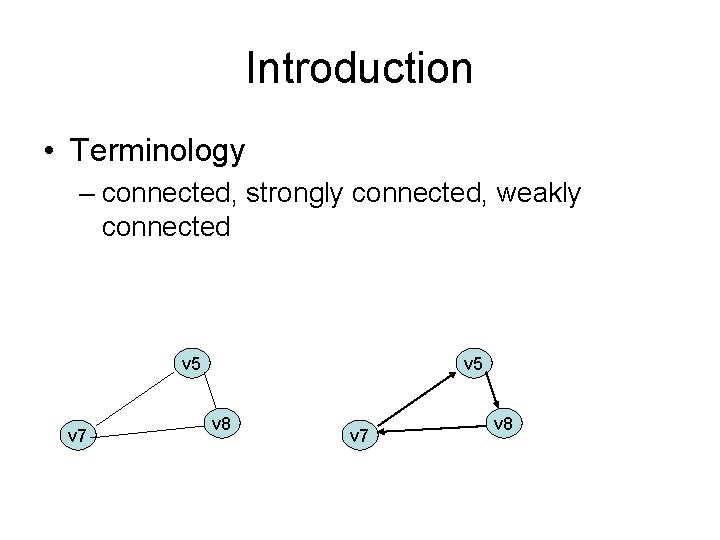
Introduction • Terminology – connected, strongly connected, weakly connected v 5 v 7 v 5 v 8 v 7 v 8

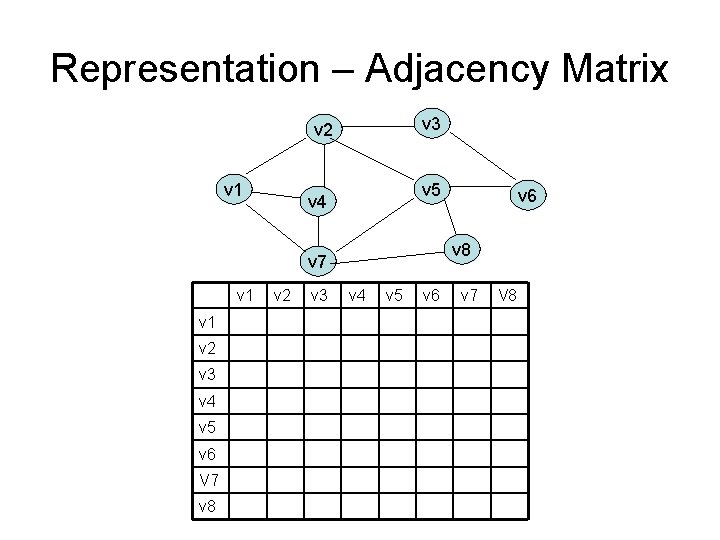
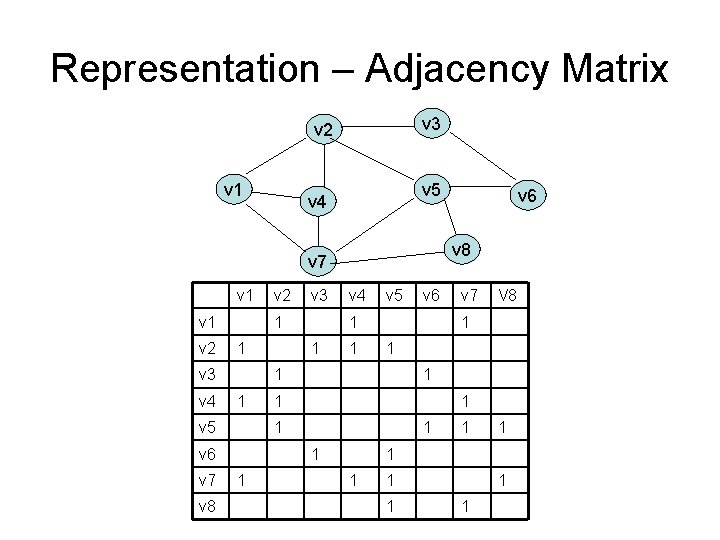
Representation – Adjacency Matrix v 3 v 2 v 1 v 5 v 4 v 8 v 7 v 1 v 2 v 3 v 4 v 5 v 6 V 7 v 8 v 2 v 3 v 6 v 4 v 5 v 6 v 7 V 8

Representation – Adjacency Matrix v 3 v 2 v 1 v 5 v 4 v 8 v 7 v 1 v 2 1 1 v 5 1 1 v 7 V 8 1 1 1 1 v 6 v 8 v 4 1 v 5 v 7 v 3 1 v 3 v 4 v 2 v 6 1 1 1 1

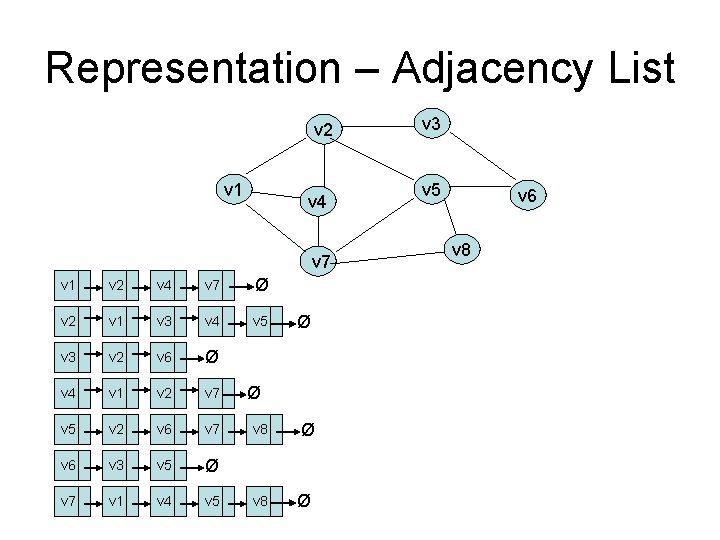
Representation – Adjacency List v 2 v 1 v 4 v 7 v 1 v 2 v 4 v 7 Ø v 2 v 1 v 3 v 4 v 5 v 3 v 2 v 6 Ø v 4 v 1 v 2 v 7 v 5 v 2 v 6 v 7 v 6 v 3 v 5 Ø v 7 v 1 v 4 v 5 Ø Ø v 8 Ø Ø v 3 v 5 v 6 v 8

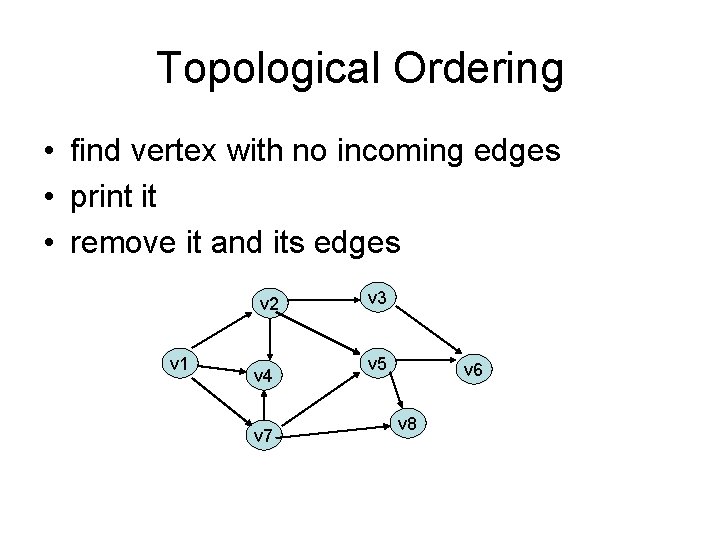
Topological Ordering • find vertex with no incoming edges • print it • remove it and its edges v 2 v 1 v 4 v 7 v 3 v 5 v 6 v 8

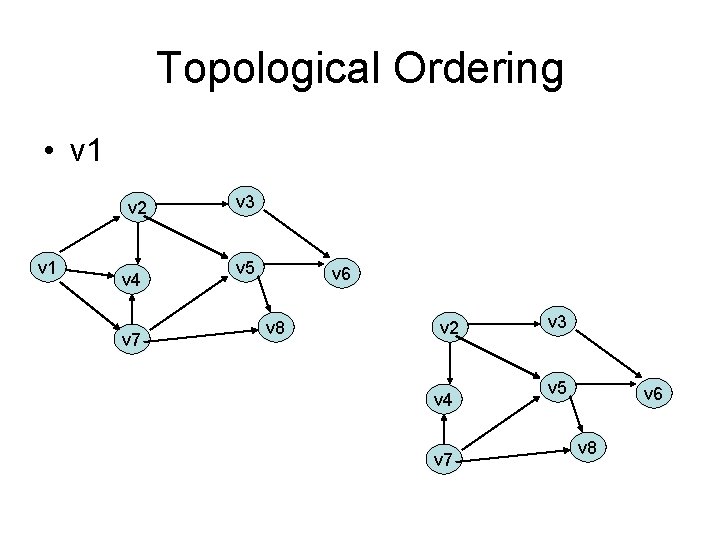
Topological Ordering • v 1 v 2 v 1 v 4 v 7 v 3 v 5 v 6 v 8 v 2 v 4 v 7 v 3 v 5 v 6 v 8

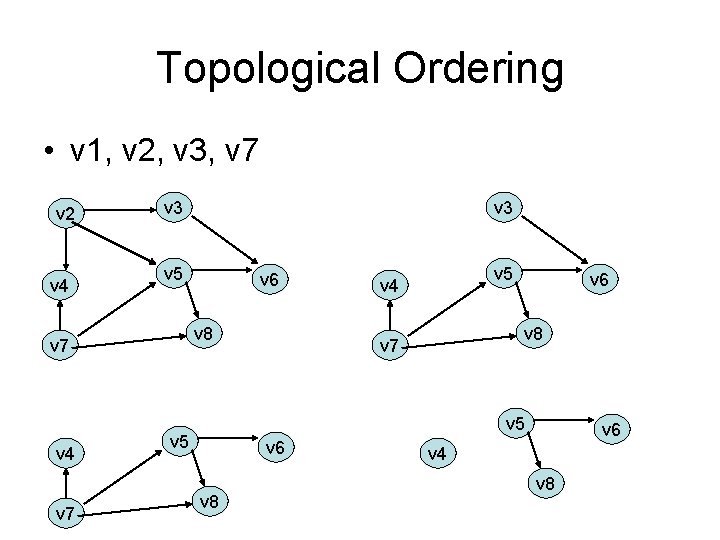
Topological Ordering • v 1, v 2, v 3, v 7 v 2 v 4 v 3 v 5 v 7 v 6 v 8 v 7 v 4 v 3 v 5 v 4 v 6 v 8 v 7 v 5 v 6 v 8 v 6 v 4 v 8

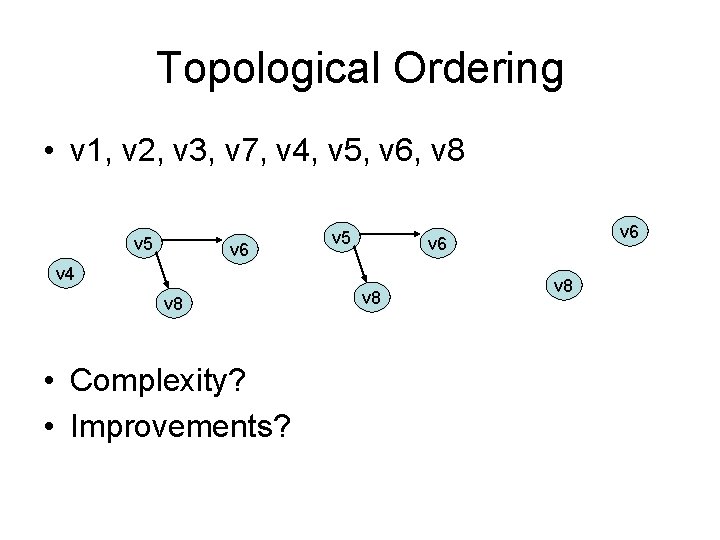
Topological Ordering • v 1, v 2, v 3, v 7, v 4, v 5, v 6, v 8 v 5 v 6 v 5 v 4 v 8 • Complexity? • Improvements? v 6 v 8

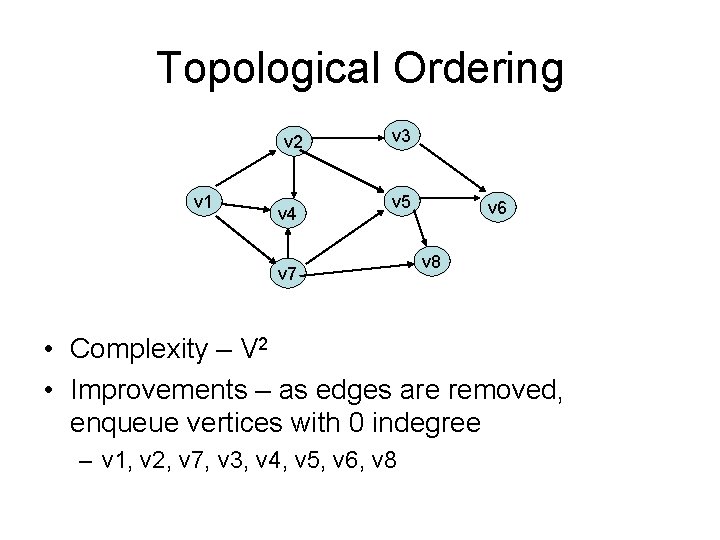
Topological Ordering v 2 v 1 v 4 v 3 v 5 v 7 v 6 v 8 • Complexity – V 2 • Improvements – as edges are removed, enqueue vertices with 0 indegree – v 1, v 2, v 7, v 3, v 4, v 5, v 6, v 8

Shortest Path Algorithms • Given as input a weighted graph G=(V, E), and a distinguished vertex, s, find the shortest weighted path from s to every other vertex in G. • Unweighted – every edge has weight 1 • Applications?

Breadth-first Search • Level-order traversal

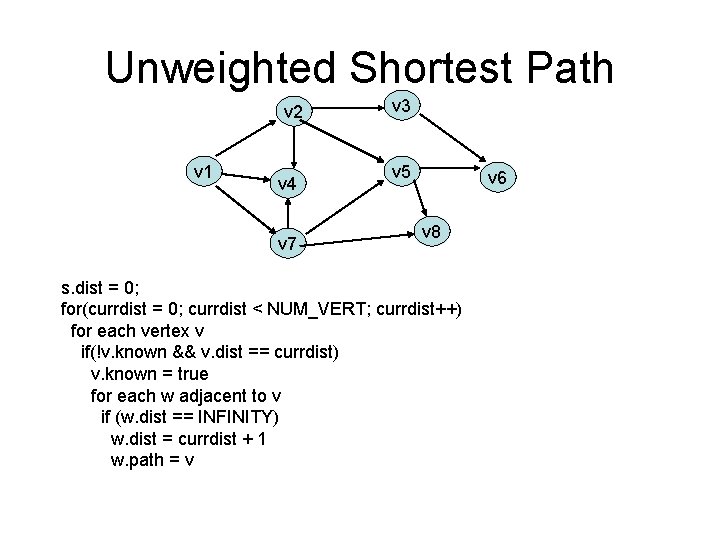
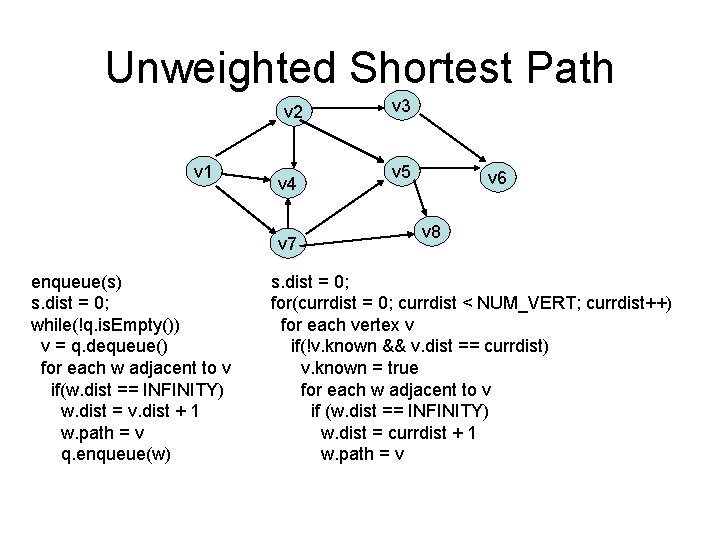
Unweighted Shortest Path v 2 v 1 v 4 v 7 v 3 v 5 v 6 v 8 s. dist = 0; for(currdist = 0; currdist < NUM_VERT; currdist++) for each vertex v if(!v. known && v. dist == currdist) v. known = true for each w adjacent to v if (w. dist == INFINITY) w. dist = currdist + 1 w. path = v

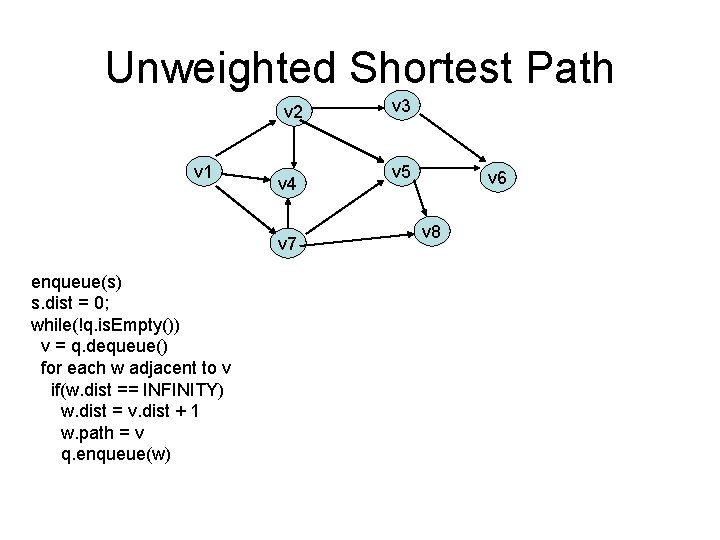
Unweighted Shortest Path v 2 v 1 v 4 v 7 enqueue(s) s. dist = 0; while(!q. is. Empty()) v = q. dequeue() for each w adjacent to v if(w. dist == INFINITY) w. dist = v. dist + 1 w. path = v q. enqueue(w) v 3 v 5 v 6 v 8

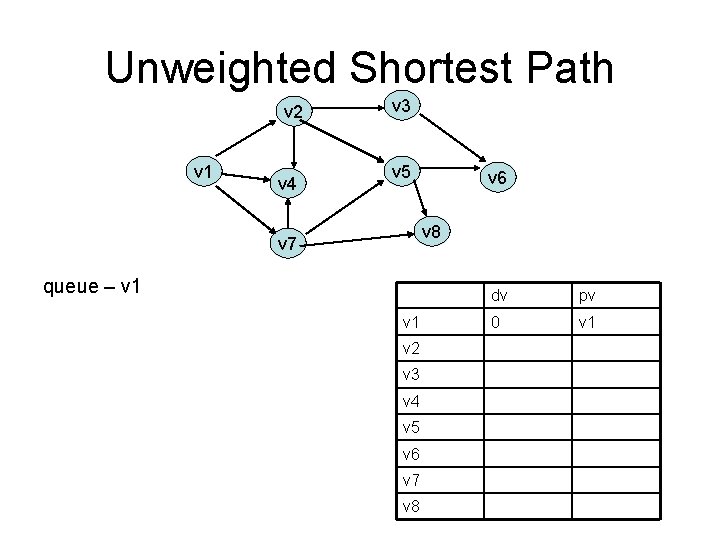
Unweighted Shortest Path v 2 v 1 v 4 v 3 v 5 v 6 v 8 v 7 queue – v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 8 dv pv 0 v 1

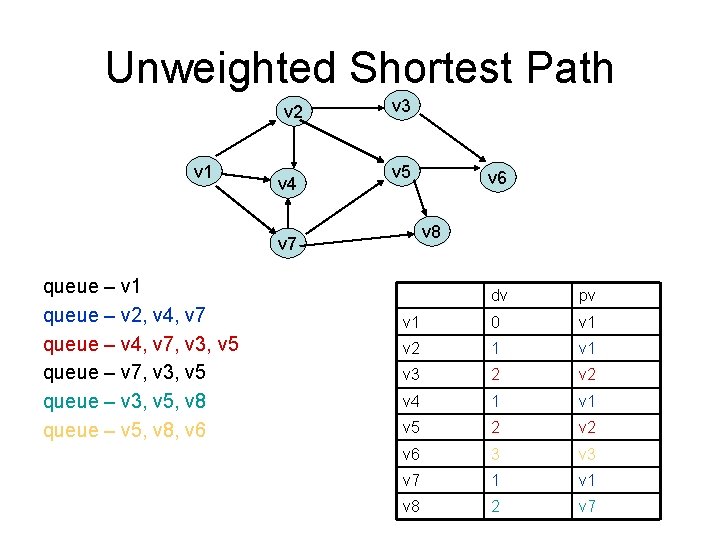
Unweighted Shortest Path v 2 v 1 v 4 v 3 v 5 v 8 v 7 queue – v 1 queue – v 2, v 4, v 7 queue – v 4, v 7, v 3, v 5 queue – v 3, v 5, v 8 queue – v 5, v 8, v 6 dv pv v 1 0 v 1 v 2 1 v 3 2 v 4 1 v 5 2 v 6 3 v 7 1 v 8 2 v 7

Unweighted Shortest Path v 2 v 1 v 4 v 7 enqueue(s) s. dist = 0; while(!q. is. Empty()) v = q. dequeue() for each w adjacent to v if(w. dist == INFINITY) w. dist = v. dist + 1 w. path = v q. enqueue(w) v 3 v 5 v 6 v 8 s. dist = 0; for(currdist = 0; currdist < NUM_VERT; currdist++) for each vertex v if(!v. known && v. dist == currdist) v. known = true for each w adjacent to v if (w. dist == INFINITY) w. dist = currdist + 1 w. path = v

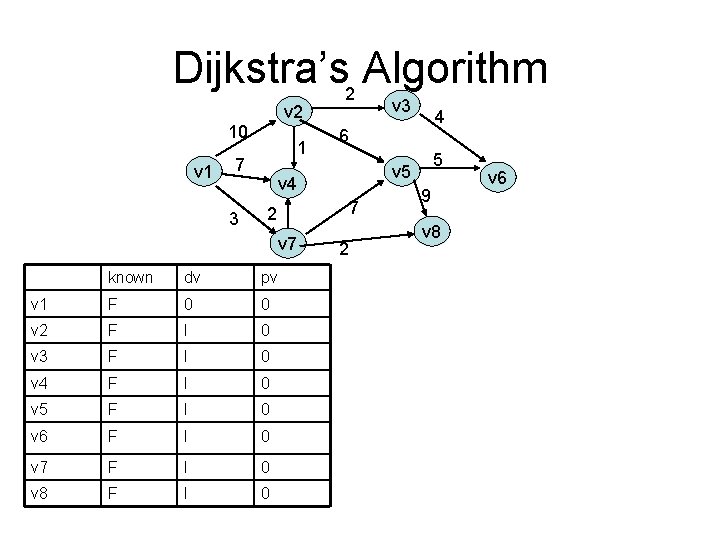
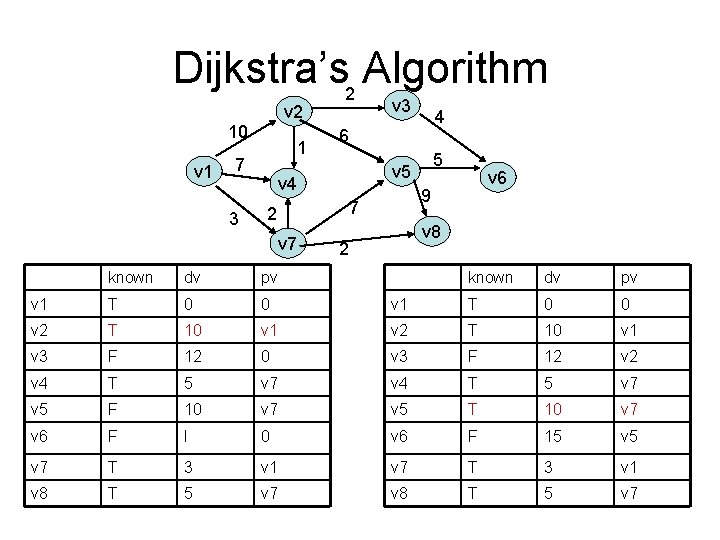
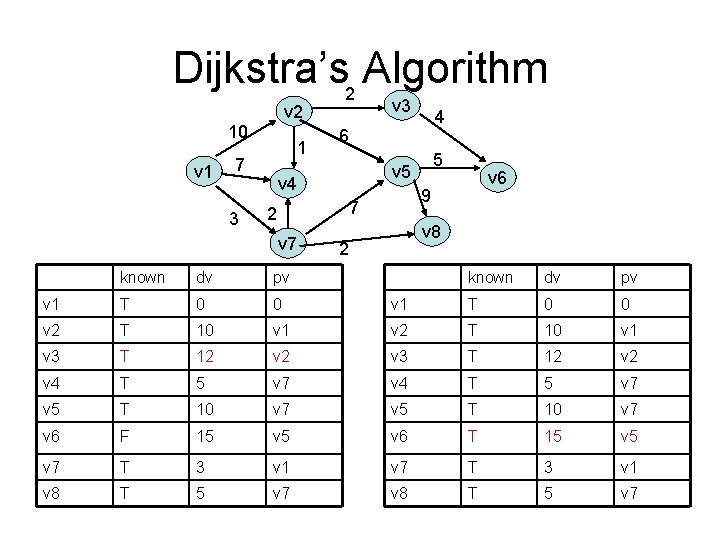
Dijkstra’s Algorithm • Weighted shortest-path first • Greedy algorithm s. dist = 0 for (; ; ) v = smallest unknown distance vertex if(v == NOT_A_VERTEX) break; v. known = true for each w adjacent to v if(!w. known) if(v. dist + cvw < w. dist) decrease(w. dist to v. dist+cvw) w. path = v

Dijkstra’s 2 Algorithm v 3 v 2 10 v 1 1 7 3 6 7 2 known dv pv v 1 F 0 0 v 2 F I 0 v 3 F I 0 v 4 F I 0 v 5 F I 0 v 6 F I 0 v 7 F I 0 v 8 F I 0 5 v 4 v 7 4 2 9 v 8 v 6

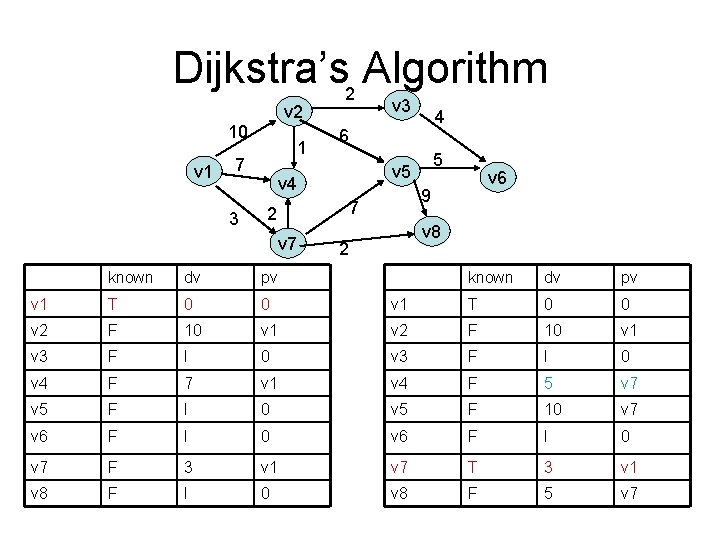
Dijkstra’s 2 Algorithm v 3 v 2 10 v 1 1 7 3 6 dv pv v 1 T 0 0 v 2 F 10 v 3 F v 4 v 6 9 7 2 known 5 v 4 v 7 4 v 8 2 known dv pv v 1 T 0 0 v 1 v 2 F 10 v 1 I 0 v 3 F I 0 F 7 v 1 v 4 F 5 v 7 v 5 F I 0 v 5 F 10 v 7 v 6 F I 0 v 7 F 3 v 1 v 7 T 3 v 1 v 8 F I 0 v 8 F 5 v 7

Dijkstra’s 2 Algorithm v 3 v 2 10 v 1 1 7 3 6 2 dv pv v 1 T 0 0 v 2 F 10 v 3 F v 4 v 6 9 7 known 5 v 4 v 7 4 v 8 2 known dv pv v 1 T 0 0 v 1 v 2 F 10 v 1 I 0 v 3 F I 0 T 5 v 7 v 4 T 5 v 7 v 5 F 10 v 7 v 6 F I 0 v 7 T 3 v 1 v 8 F 5 v 7 v 8 T 5 v 7

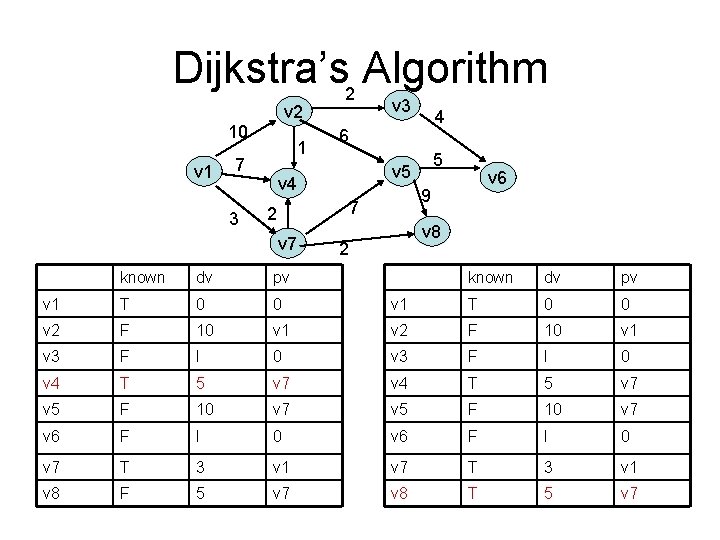
Dijkstra’s 2 Algorithm v 3 v 2 10 v 1 1 7 3 6 dv pv v 1 T 0 0 v 2 T 10 v 3 F v 4 v 6 9 7 2 known 5 v 4 v 7 4 v 8 2 known dv pv v 1 T 0 0 v 1 v 2 T 10 v 1 12 0 v 3 F 12 v 2 T 5 v 7 v 4 T 5 v 7 v 5 F 10 v 7 v 5 T 10 v 7 v 6 F I 0 v 6 F 15 v 7 T 3 v 1 v 8 T 5 v 7

Dijkstra’s 2 Algorithm v 3 v 2 10 v 1 1 7 3 6 2 dv pv v 1 T 0 0 v 2 T 10 v 3 T v 4 v 6 9 7 known 5 v 4 v 7 4 v 8 2 known dv pv v 1 T 0 0 v 1 v 2 T 10 v 1 12 v 3 T 12 v 2 T 5 v 7 v 4 T 5 v 7 v 5 T 10 v 7 v 6 F 15 v 6 T 15 v 7 T 3 v 1 v 8 T 5 v 7

Running time – Dijkstra’s • Simplementation – O(E + V 2) • Improvements – Use a priority queue – Smallest unknown distance vertex log V (V times) – decrease log V (E times)

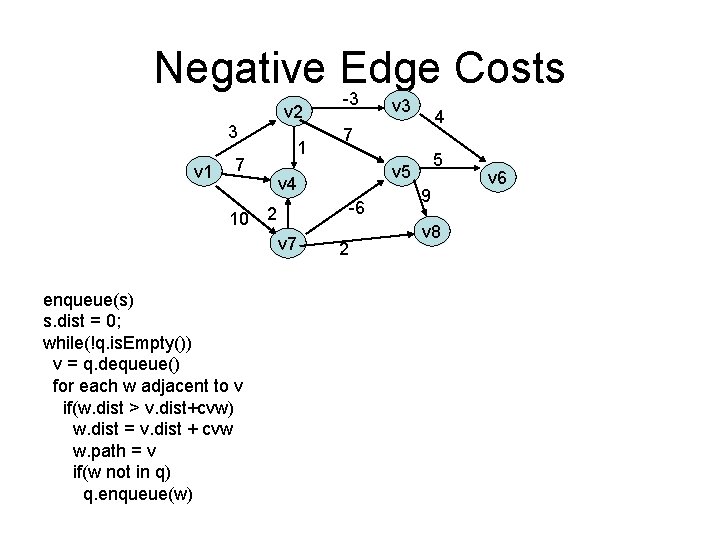
Negative Edge Costs v 2 3 v 1 7 1 -3 5 v 5 -6 10 2 enqueue(s) s. dist = 0; while(!q. is. Empty()) v = q. dequeue() for each w adjacent to v if(w. dist > v. dist+cvw) w. dist = v. dist + cvw w. path = v if(w not in q) q. enqueue(w) 4 7 v 4 v 7 v 3 2 9 v 8 v 6

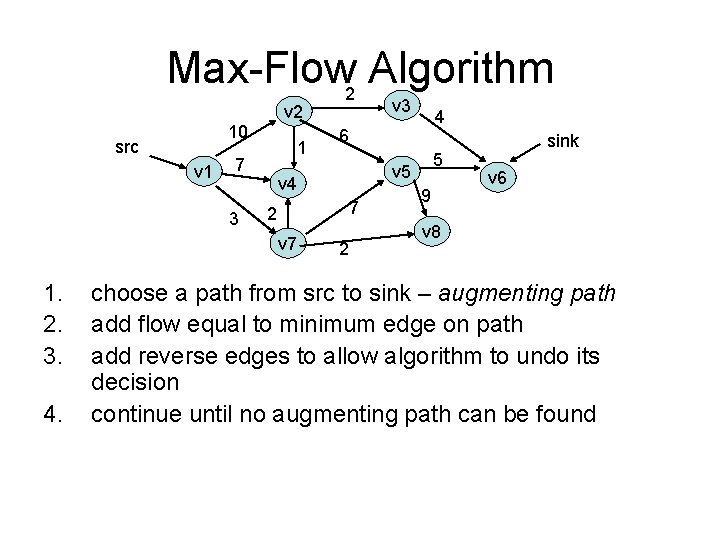
Network Flow • Determine maximum flow from source to sink in a directed graph where each edge has given capacity – capacity cv, w is maximum flow for edge (v, w) – total flow coming in must = total flow going out • Example applications?

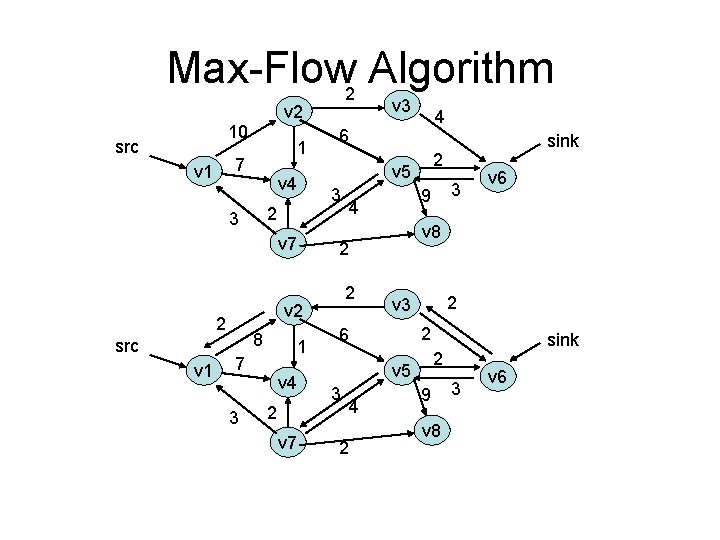
Max-Flow 2 Algorithm v 3 v 2 10 src v 1 1 7 3 1. 2. 3. 4. 6 5 v 4 7 2 v 7 4 2 9 sink v 6 v 8 choose a path from src to sink – augmenting path add flow equal to minimum edge on path add reverse edges to allow algorithm to undo its decision continue until no augmenting path can be found

Max-Flow 2 Algorithm v 3 v 2 10 src 1 7 v 1 v 4 2 3 v 7 src v 1 6 3 8 1 7 3 v 4 2 v 7 2 2 v 3 2 6 4 sink 2 v 5 2 v 6 v 8 2 3 3 9 4 sink 2 v 5 v 2 2 4 9 v 8 3 v 6

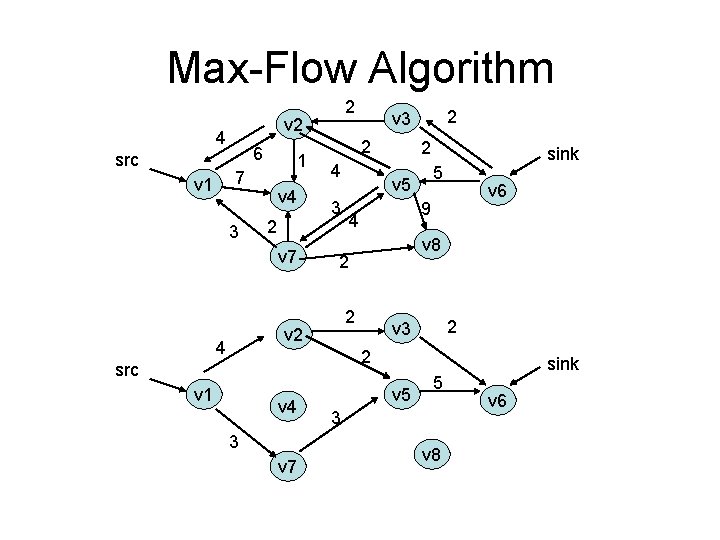
Max-Flow Algorithm v 2 4 src 6 1 7 v 1 2 3 v 4 2 v 7 2 4 4 2 sink 5 v 5 3 v 6 9 4 v 8 2 2 v 3 2 src v 1 v 4 3 v 7 v 5 5 3 v 8 sink v 6

Algorithm Complexity • O(f * E) • Can be bad if f is large – Improve by choosing augmenting path that increases flow by largest amount

Minimum Spanning Tree • Find a tree (acyclic graph) that covers every vertex and has minimum cost – Number of edges in tree will be V-1

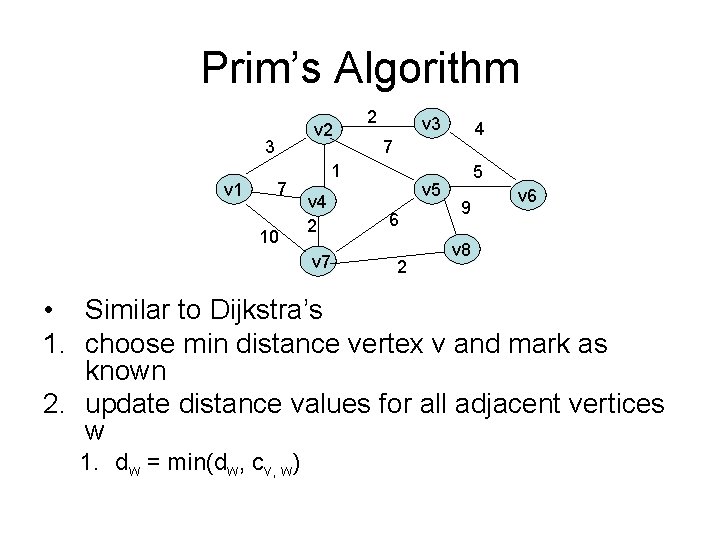
Prim’s Algorithm v 2 3 v 1 7 10 2 v 3 7 1 v 4 2 v 7 4 v 5 6 2 5 9 v 6 v 8 • Similar to Dijkstra’s 1. choose min distance vertex v and mark as known 2. update distance values for all adjacent vertices w 1. dw = min(dw, cv, w)

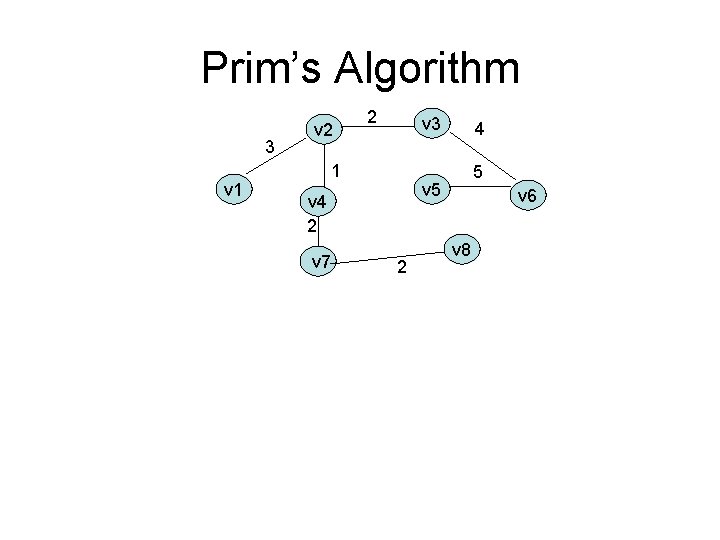
Prim’s Algorithm 3 v 1 v 2 2 v 3 1 5 v 4 2 v 7 4 2 v 6 v 8

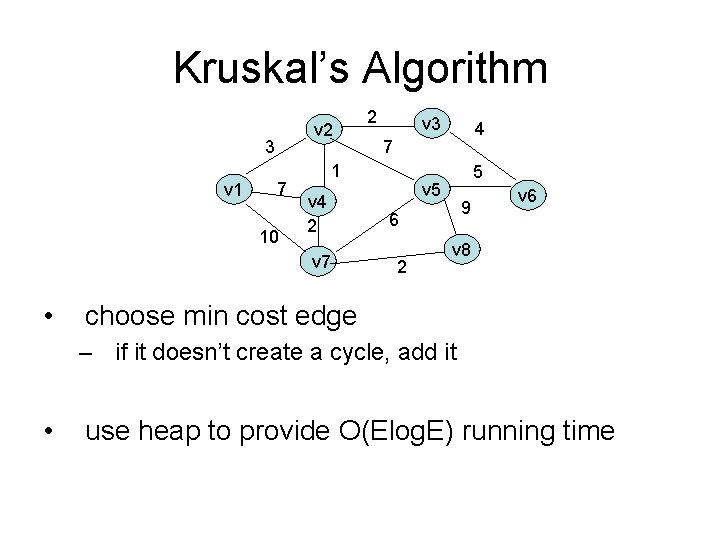
Kruskal’s Algorithm v 2 3 v 1 7 10 v 3 v 4 2 4 7 1 v 7 • 2 5 v 5 9 6 2 v 6 v 8 choose min cost edge – if it doesn’t create a cycle, add it • use heap to provide O(Elog. E) running time

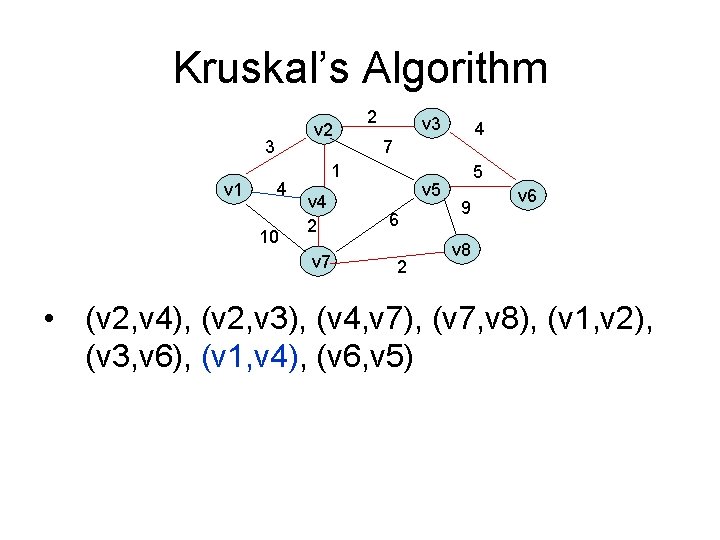
Kruskal’s Algorithm v 2 3 v 1 4 10 2 v 3 7 1 v 4 2 v 7 4 v 5 6 2 5 9 v 6 v 8 • (v 2, v 4), (v 2, v 3), (v 4, v 7), (v 7, v 8), (v 1, v 2), (v 3, v 6), (v 1, v 4), (v 6, v 5)

Depth-First Search • Generalization of preorder traversal dfs(Vertex v) v. visited = true for each w adjacent to v if(!w. visited) dfs(w)