Graph Algorithms Continued Kruskals Algorithm CutlerHead Kruskals Algorithm


- Slides: 9

Graph Algorithms Continued Kruskal’s Algorithm Cutler/Head

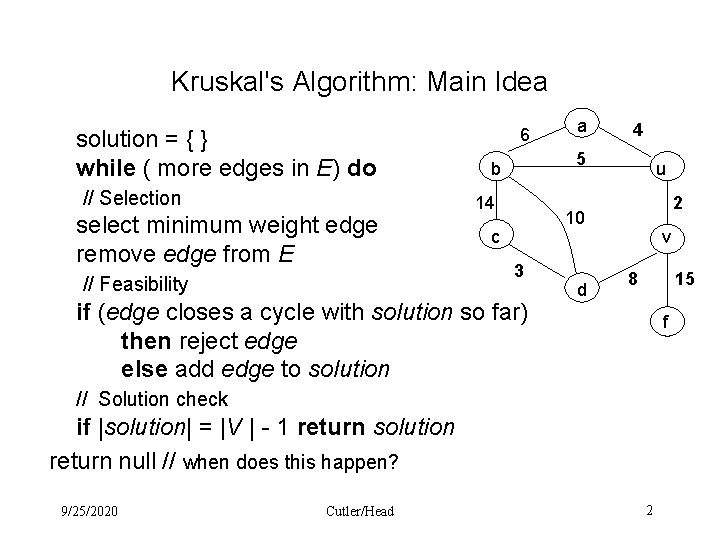
Kruskal's Algorithm: Main Idea solution = { } while ( more edges in E) do // Selection select minimum weight edge remove edge from E // Feasibility 6 a 4 5 b 14 u 2 10 c 3 if (edge closes a cycle with solution so far) then reject edge else add edge to solution d v 8 15 f // Solution check if |solution| = |V | - 1 return solution return null // when does this happen? 9/25/2020 Cutler/Head 2

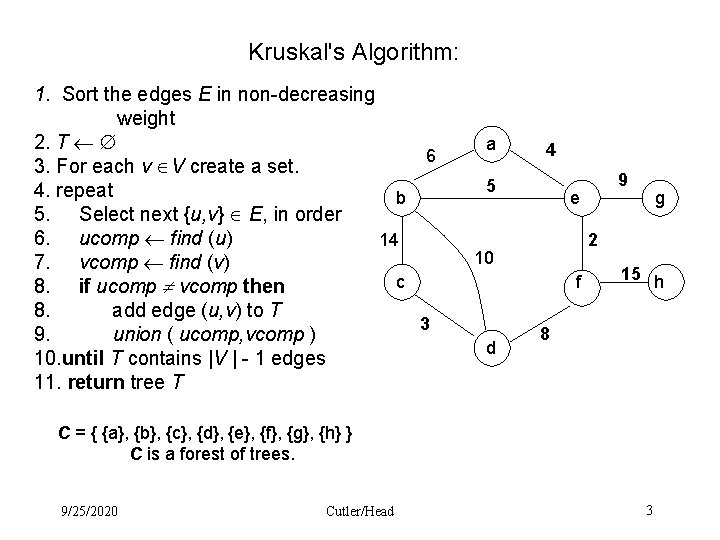
Kruskal's Algorithm: 1. Sort the edges E in non-decreasing weight 2. T 6 3. For each v V create a set. 4. repeat b 5. Select next {u, v} E, in order 6. ucomp find (u) 14 7. vcomp find (v) c 8. if ucomp vcomp then 8. add edge (u, v) to T 3 9. union ( ucomp, vcomp ) 10. until T contains |V | - 1 edges 11. return tree T a 4 5 e g 2 10 f d 9 15 h 8 C = { {a}, {b}, {c}, {d}, {e}, {f}, {g}, {h} } C is a forest of trees. 9/25/2020 Cutler/Head 3

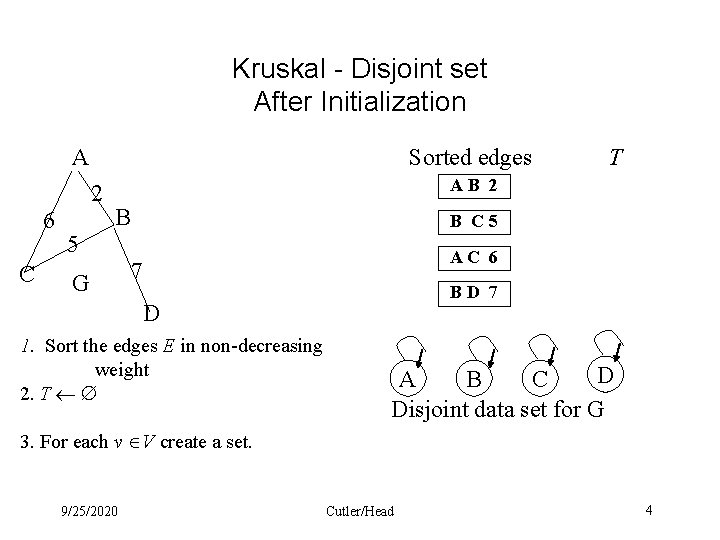
Kruskal - Disjoint set After Initialization A Sorted edges 2 6 C T AB 2 B B C 5 5 G AC 6 7 BD 7 D 1. Sort the edges E in non-decreasing weight 2. T D A B C Disjoint data set for G 3. For each v V create a set. 9/25/2020 Cutler/Head 4

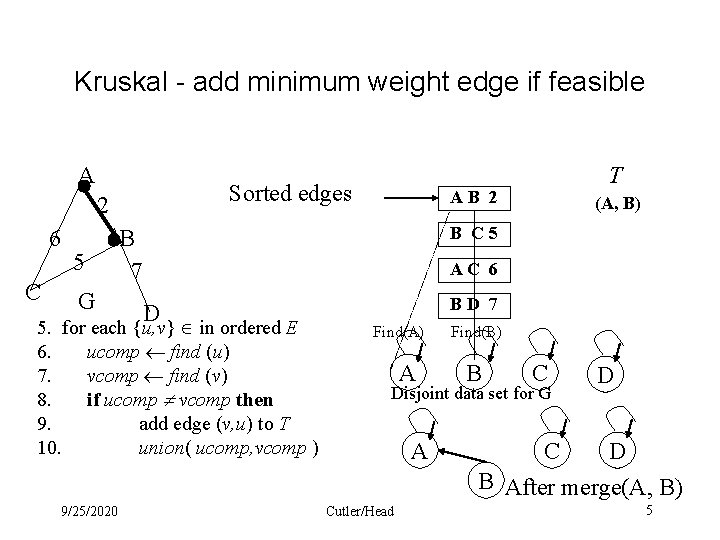
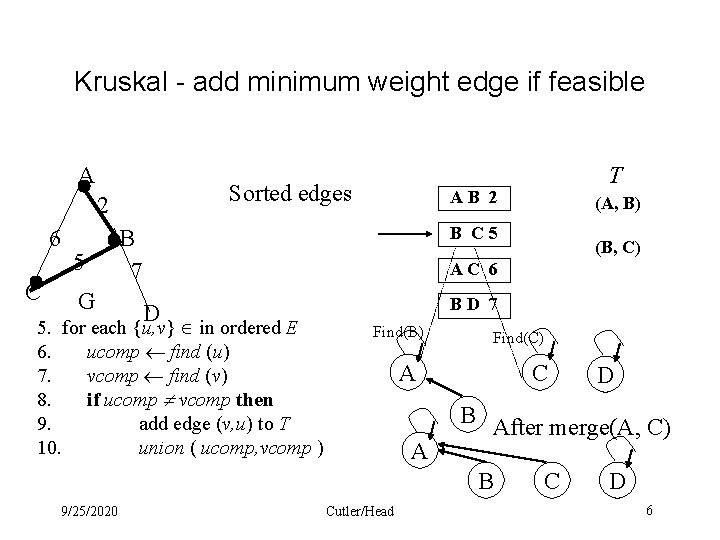
Kruskal - add minimum weight edge if feasible A Sorted edges 2 6 C 5 G T AB 2 (A, B) B C 5 B 7 AC 6 D 5. for each {u, v} in ordered E 6. ucomp find (u) 7. vcomp find (v) 8. if ucomp vcomp then 9. add edge (v, u) to T 10. union( ucomp, vcomp ) BD 7 Find(A) A Find(B) B C Disjoint data set for G A C D D B After merge(A, B) 9/25/2020 Cutler/Head 5

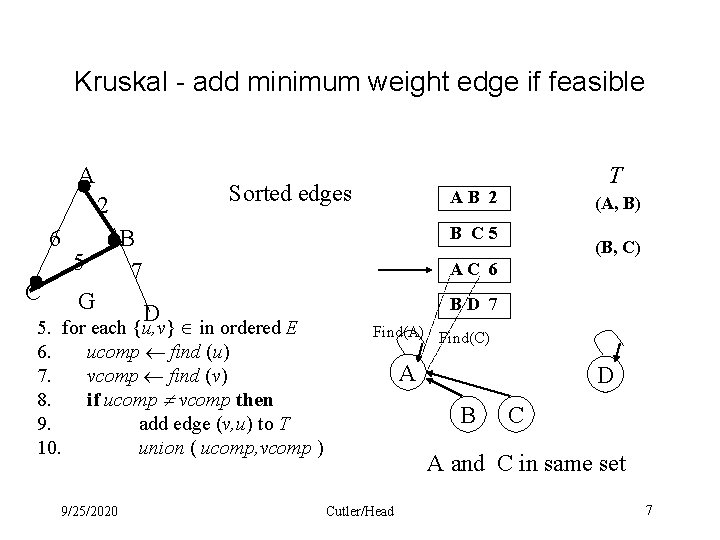
Kruskal - add minimum weight edge if feasible A Sorted edges 2 6 C 5 G AB 2 (A, B) B C 5 B 7 (B, C) AC 6 D 5. for each {u, v} in ordered E 6. ucomp find (u) 7. vcomp find (v) 8. if ucomp vcomp then 9. add edge (v, u) to T 10. union ( ucomp, vcomp ) BD 7 Find(B) Find(C) A C B A Cutler/Head D After merge(A, C) B 9/25/2020 T C D 6

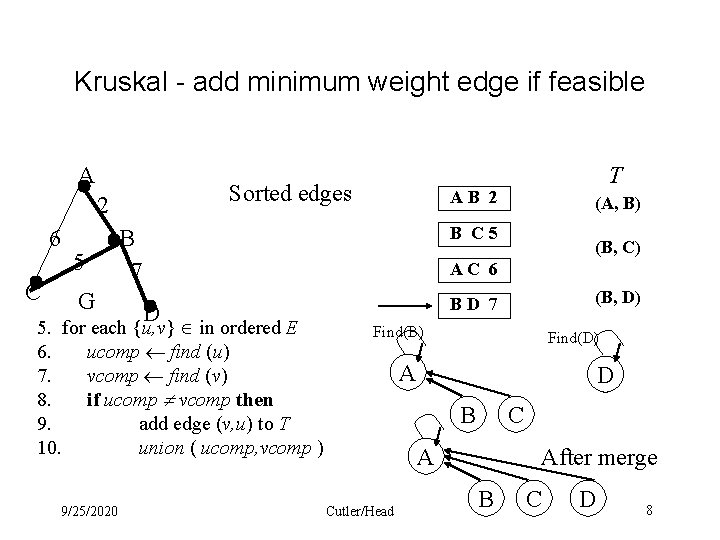
Kruskal - add minimum weight edge if feasible A Sorted edges 2 6 C 5 G AB 2 (A, B) B C 5 B 7 (B, C) AC 6 D 5. for each {u, v} in ordered E 6. ucomp find (u) 7. vcomp find (v) 8. if ucomp vcomp then 9. add edge (v, u) to T 10. union ( ucomp, vcomp ) 9/25/2020 T BD 7 Find(A) Find(C) A D B C A and C in same set Cutler/Head 7

Kruskal - add minimum weight edge if feasible A Sorted edges 2 6 C 5 G AB 2 (A, B) B C 5 B 7 (B, C) AC 6 D 5. for each {u, v} in ordered E 6. ucomp find (u) 7. vcomp find (v) 8. if ucomp vcomp then 9. add edge (v, u) to T 10. union ( ucomp, vcomp ) 9/25/2020 T (B, D) BD 7 Find(B) Find(D) A D B C A Cutler/Head After merge B C D 8

Kruskal's Algorithm: Time Analysis Kruskal ( G ) 1. Sort the edges E in non-decreasing weight 2. T 3. For each v V create a set. 4. repeat 5. {u, v} E, in order 6. ucomp find (u) 7. vcomp find (v) 8. if ucomp vcomp then 9. add edge (v, u) to T 10. union ( ucomp, vcomp ) 11. until T contains |V | - 1 edges 12. return tree T 9/25/2020 Cutler/Head Count 1 = ( E lg E ) Count 2= (1) Count 3= ( V ) Count 4 = O( E ) Using Disjoint set-height and path compression Count 4(6+7+10)= O((E +V) (V)) Sorting dominates the runtime. We get T( E, V ) = ( E lg E), so for a sparse graph we get ( V lg V) for a dense graph we get ( V 2 lg V 2) = ( V 2 lg V) 9