Graph Algorithms and Their Applications on Computer Networks

Graph Algorithms and Their Applications on Computer Networks Neil Tang 2/6/2010 1

Outline Ø Network Model Ø Link and Path Costs Ø Routing Problems Ø Dijkstra’s Shortest Path Algorithm Ø Constrained Shortest Path Algorithms Ø Another Approach: LP and ILP CS 223 Advanced Data Structures and Algorithms 2

Network Model Ø A network is usually modeled as a graph such that the networking problems, such as routing and scheduling, can be transformed to the corresponding problems in a graph and solved by algorithms in graph theory. Ø A vertex in the graph represents a router. Ø In a wired network, there is an edge (A, B) between a pair of vertices A and B if there is a physical link in between. Ø Disk graph: In a wireless network, there is an edge (A, B) between a pair of vertices A and B if their Euclidean distance is no more than the transmission range of node A. CS 223 Advanced Data Structures and Algorithms 3

Link and Path Cost Ø There is usually one or multiple cost parameters associated with each link, which indicate its transmission cost, bandwidth, delay and so on. Ø Some of parameters are bottleneck parameters (e. g. bandwidth), i. e. , the cost of the path in terms of this parameter depends on the minimum link cost along the path. Ø Some of parameters are additive parameters (e. g. delay), i. e. , the cost of the path in terms of this parameter is equal to the summation of the costs of all links along the path. CS 223 Advanced Data Structures and Algorithms 4

Routing Problems Ø Basic routing problem: Given a source and a destination, the basic routing problem seeks a source-destination route such that it has the minimum cost among all possible source-destination routes. Ø Qo. S routing problem: Given a source and destination along with one or multiple Qo. S constrains (e. g, bandwidth, delay), a Qo. S routing problem seeks a source-destination route such that it has the minimum cost among all source-destination routes which can satisfy all Qo. S constraints. CS 223 Advanced Data Structures and Algorithms 5

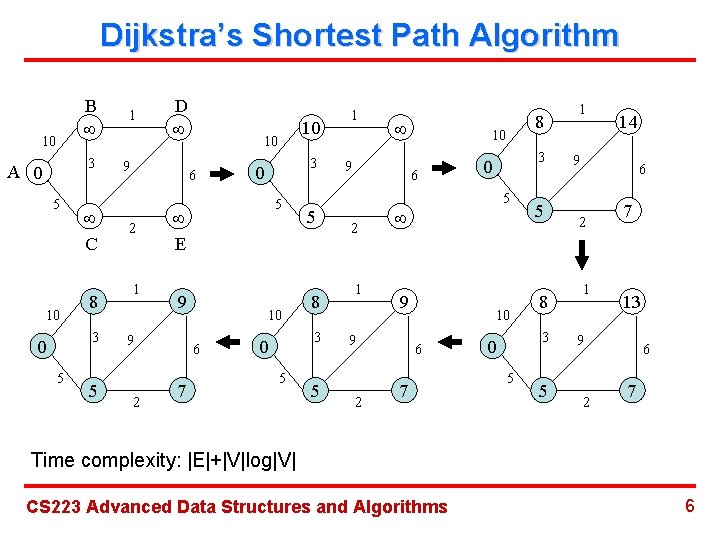
Dijkstra’s Shortest Path Algorithm 10 B 3 A 0 5 10 C 8 3 0 5 5 1 D 9 10 6 2 1 0 E 9 2 3 5 9 10 6 7 10 5 8 3 0 5 5 1 9 10 6 2 1 9 2 3 0 5 9 10 6 7 8 5 8 3 0 5 5 1 14 9 6 2 1 7 13 9 2 6 7 Time complexity: |E|+|V|log|V| CS 223 Advanced Data Structures and Algorithms 6

Typical Qo. S Routing Problems Ø Find a minimum cost path subject to a bottleneck (e. g. , bandwidth) constraint. Ø Find a minimum cost path subject to an additive (e. g. delay) constraint. This problem is NP-hard. CS 223 Advanced Data Structures and Algorithms 7

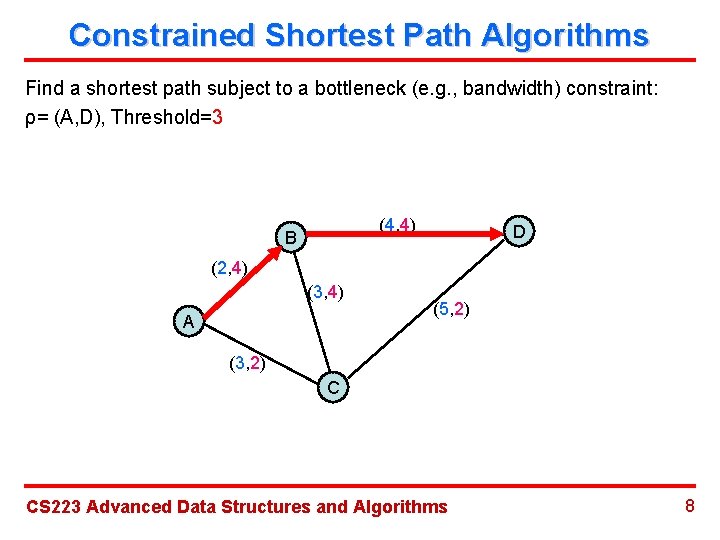
Constrained Shortest Path Algorithms Find a shortest path subject to a bottleneck (e. g. , bandwidth) constraint: ρ= (A, D), Threshold=3 (4, 4) B D (2, 4) (3, 4) A (5, 2) (3, 2) C CS 223 Advanced Data Structures and Algorithms 8

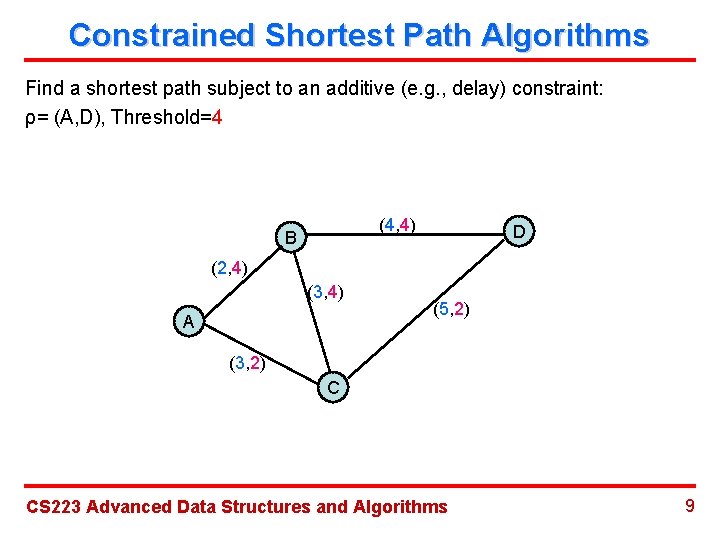
Constrained Shortest Path Algorithms Find a shortest path subject to an additive (e. g. , delay) constraint: ρ= (A, D), Threshold=4 (4, 4) B D (2, 4) (3, 4) A (5, 2) (3, 2) C CS 223 Advanced Data Structures and Algorithms 9

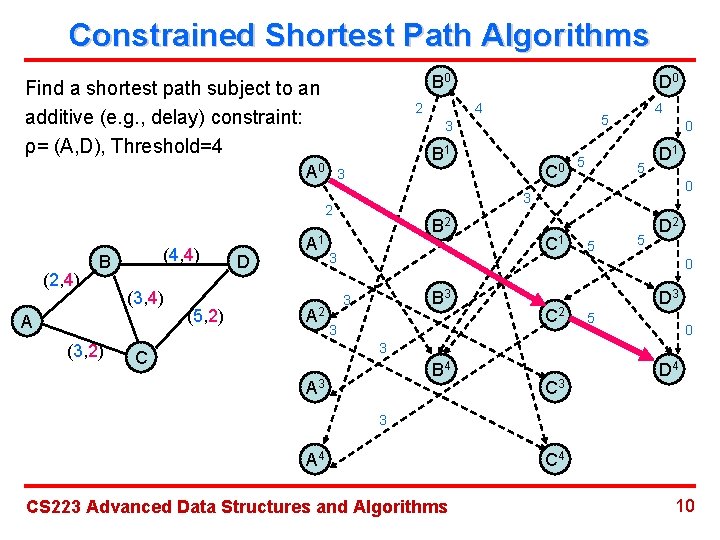
Constrained Shortest Path Algorithms B 0 Find a shortest path subject to an additive (e. g. , delay) constraint: ρ= (A, D), Threshold=4 2 (2, 4) (4, 4) (3, 4) A (3, 2) (5, 2) D A 2 4 5 B 1 5 C 0 3 0 5 D 1 0 3 2 B 4 3 A 0 A 1 D 0 B 2 3 C 1 5 5 D 2 0 B 3 3 3 C 2 D 3 5 0 3 C B 4 A 3 C 3 D 4 3 A 4 CS 223 Advanced Data Structures and Algorithms C 4 10

Maximum Flow Problem - LP CS 223 Advanced Data Structures and Algorithms 11

Multi-Commodity Flow Problem - LP CS 223 Advanced Data Structures and Algorithms 12

Shortest Path Problem - ILP CS 223 Advanced Data Structures and Algorithms 13

Constrained Shortest Path Problem - ILP CS 223 Advanced Data Structures and Algorithms 14