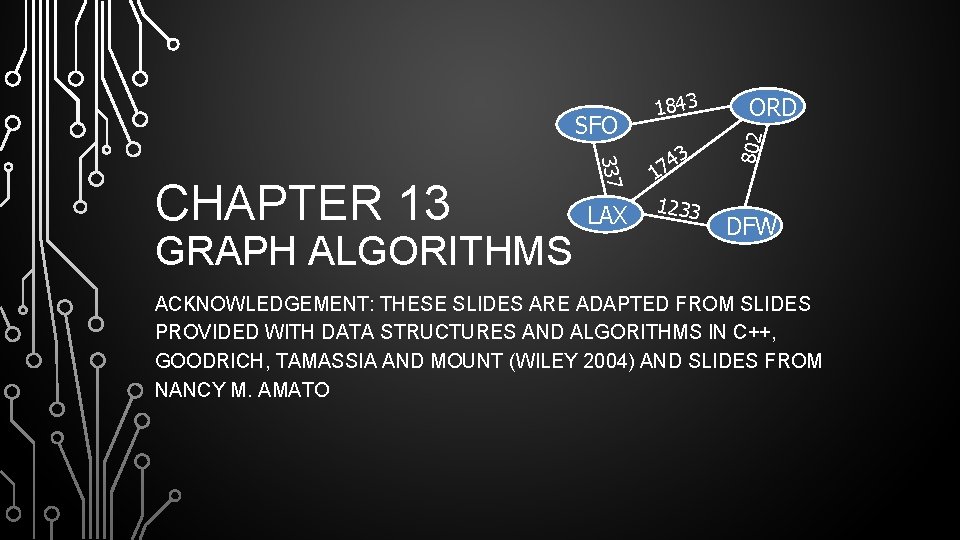
GRAPH ALGORITHMS 337 CHAPTER 13 LAX 4 17

GRAPH ALGORITHMS 337 CHAPTER 13 LAX 4 17 3 1233 ORD 802 SFO 1843 DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO

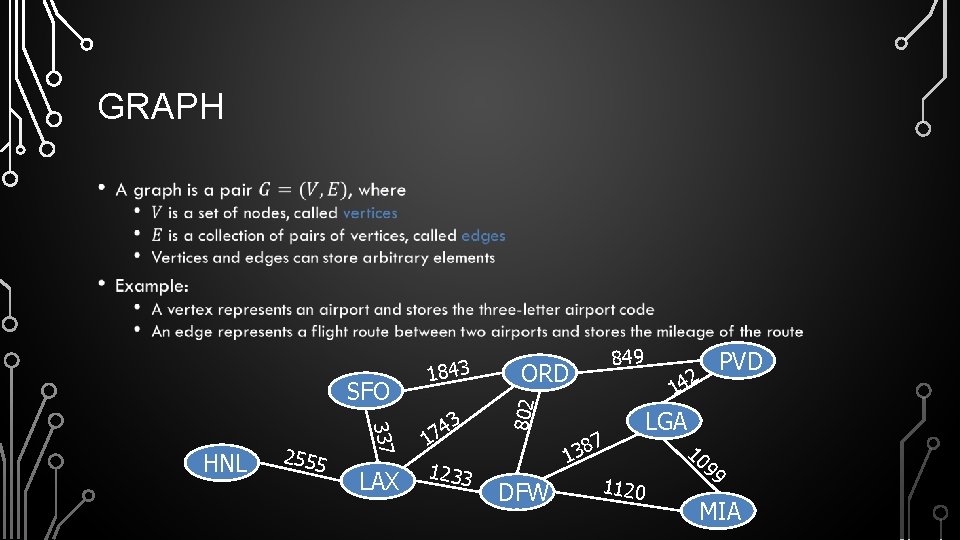
GRAPH • 337 HNL 2555 LAX 3 4 17 1233 849 ORD 14 802 SFO 1843 7 138 DFW 1120 PVD 2 LGA 10 99 MIA

EDGE & GRAPH TYPES • flight ORD AA 1206 802 miles DFW flight ORD route 802 miles DFW

APPLICATIONS • Electronic circuits • Printed circuit board • Integrated circuit • Transportation networks • Highway network • Flight network • Computer networks • Local area network • Internet • Web • Databases • Entity-relationship diagram

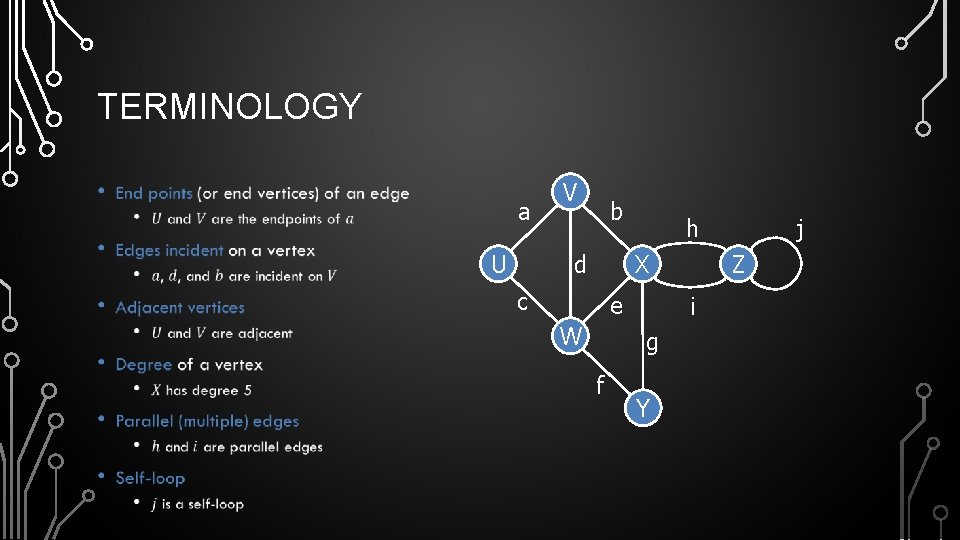
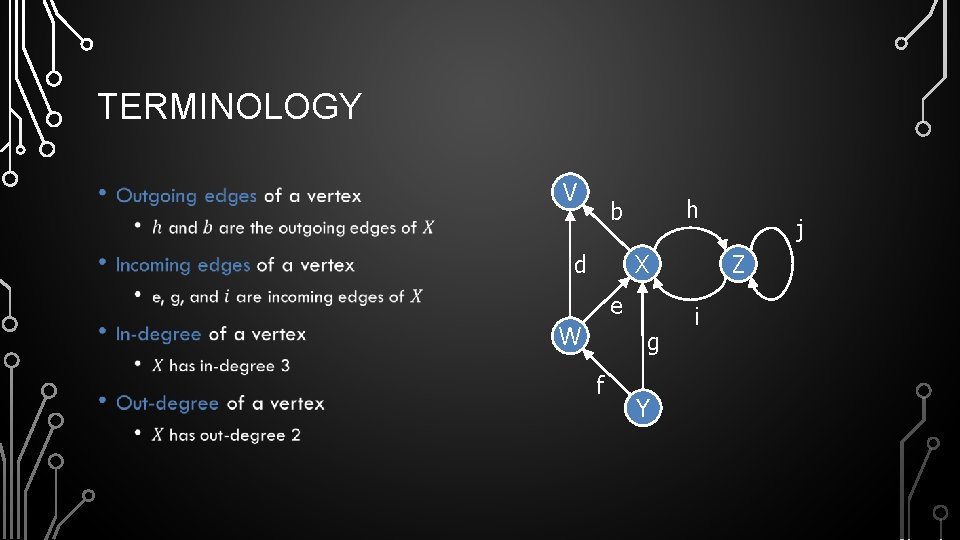
TERMINOLOGY • a U V b h X d c e W f Z i g Y j

TERMINOLOGY • V h b Z X d e W g f Y j i

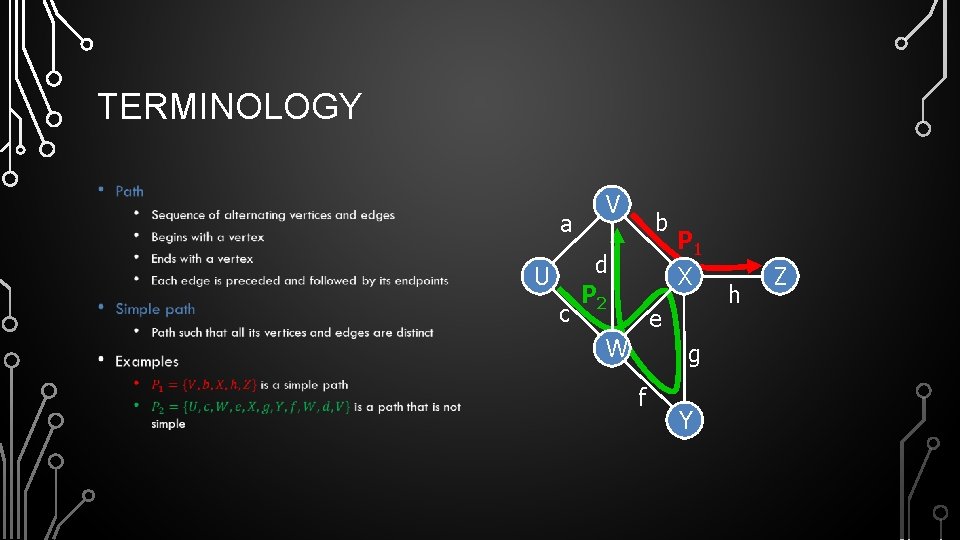
TERMINOLOGY • a U c V b d P 2 P 1 X e W g f Y h Z

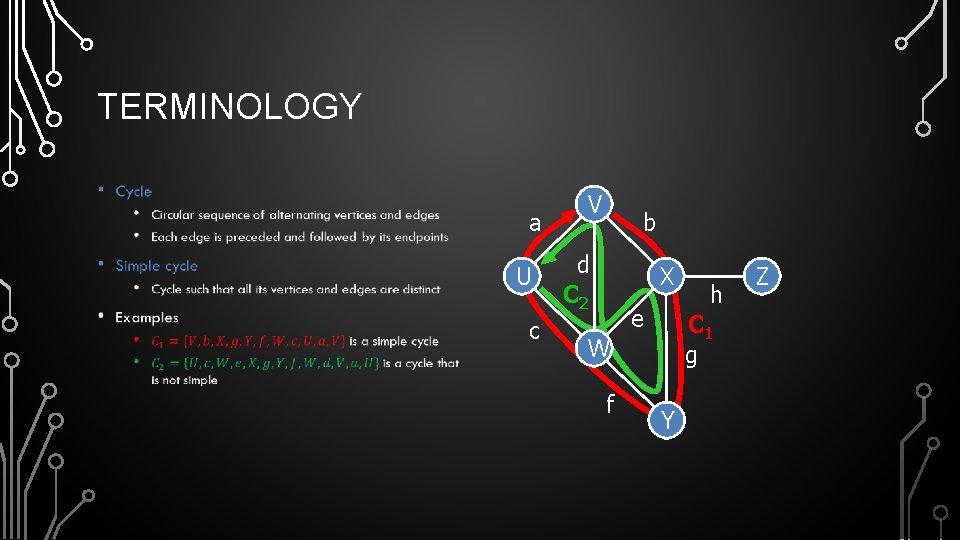
TERMINOLOGY • a U c V b d C 2 X e C 1 g W f h Y Z

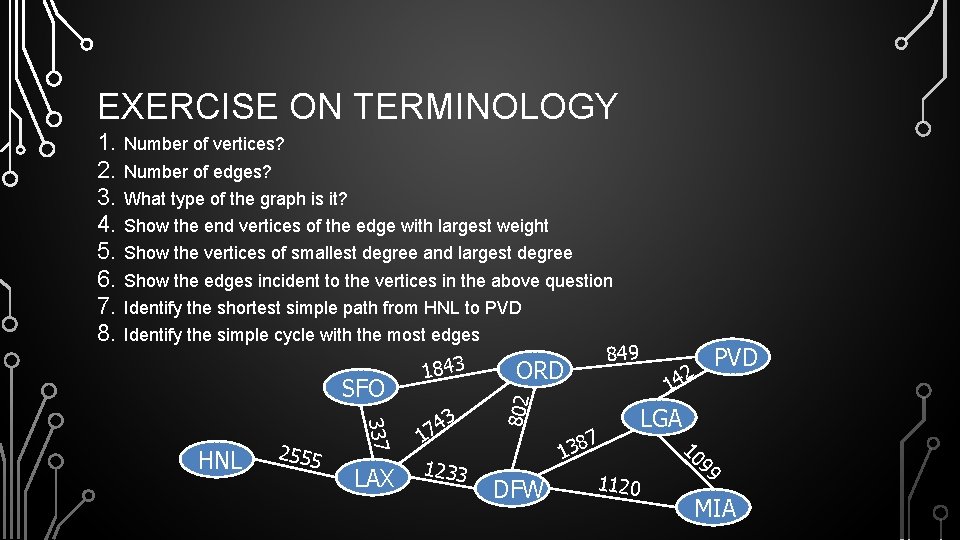
EXERCISE ON TERMINOLOGY Number of vertices? Number of edges? What type of the graph is it? Show the end vertices of the edge with largest weight Show the vertices of smallest degree and largest degree Show the edges incident to the vertices in the above question Identify the shortest simple path from HNL to PVD Identify the simple cycle with the most edges SFO 337 HNL 2555 LAX 1843 3 4 17 1233 849 ORD 802 1. 2. 3. 4. 5. 6. 7. 8. DFW 14 7 8 3 1 1120 PVD 2 LGA 10 99 MIA

EXERCISE PROPERTIES OF UNDIRECTED GRAPHS • • A graph with given number of vertices (4) and maximum number of edges

EXERCISE PROPERTIES OF UNDIRECTED GRAPHS • • A graph with given number of vertices (4) and maximum number of edges

EXERCISE PROPERTIES OF DIRECTED GRAPHS • • A graph with given number of vertices (4) and maximum number of edges

EXERCISE PROPERTIES OF DIRECTED GRAPHS • • A graph with given number of vertices (4) and maximum number of edges

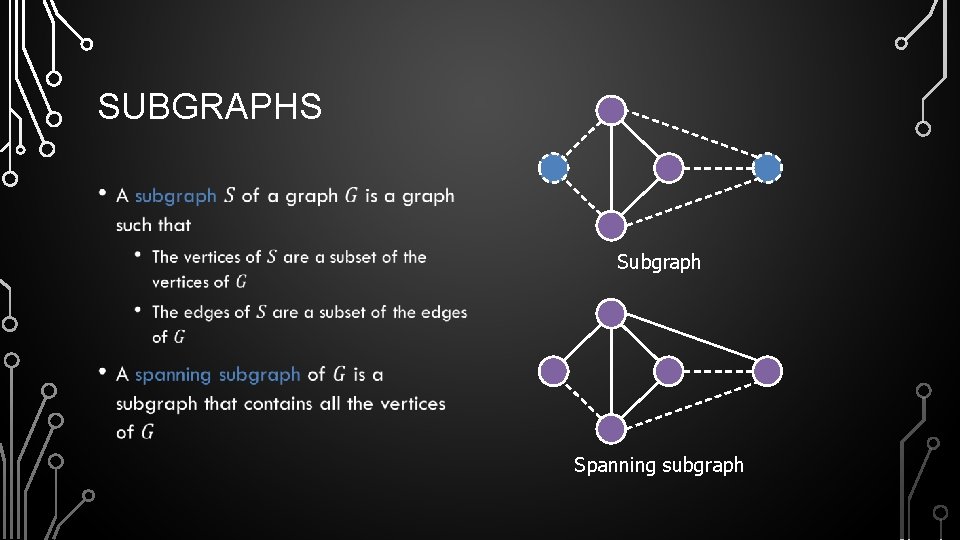
SUBGRAPHS • Subgraph Spanning subgraph

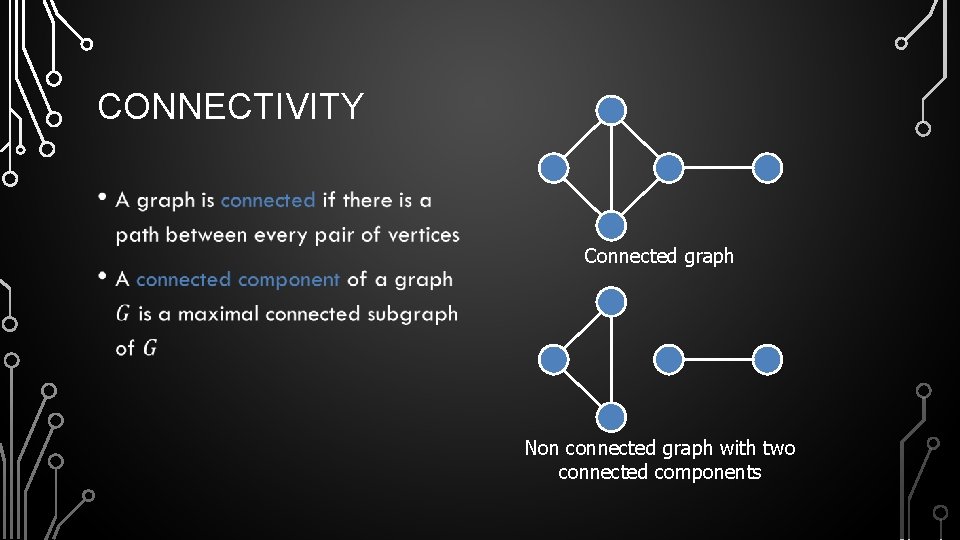
CONNECTIVITY • Connected graph Non connected graph with two connected components

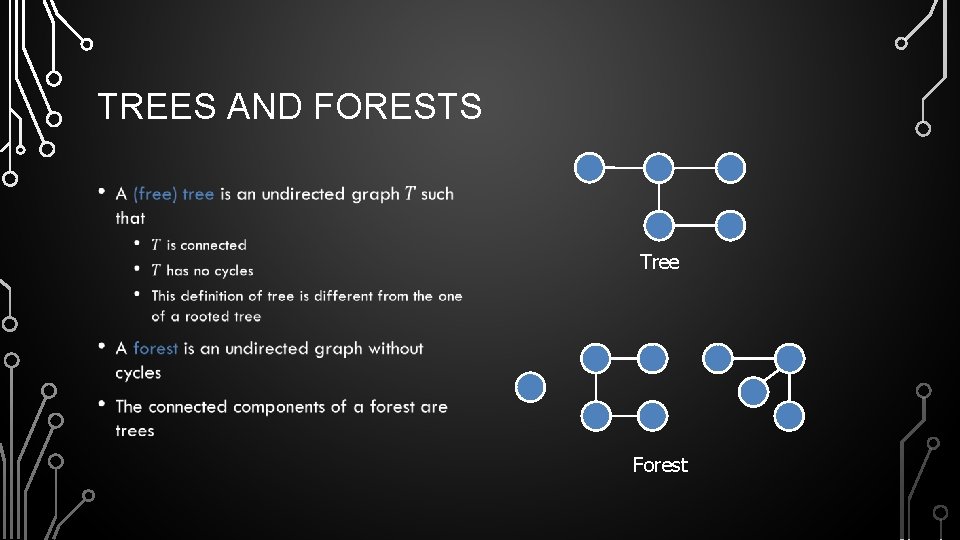
TREES AND FORESTS • Tree Forest

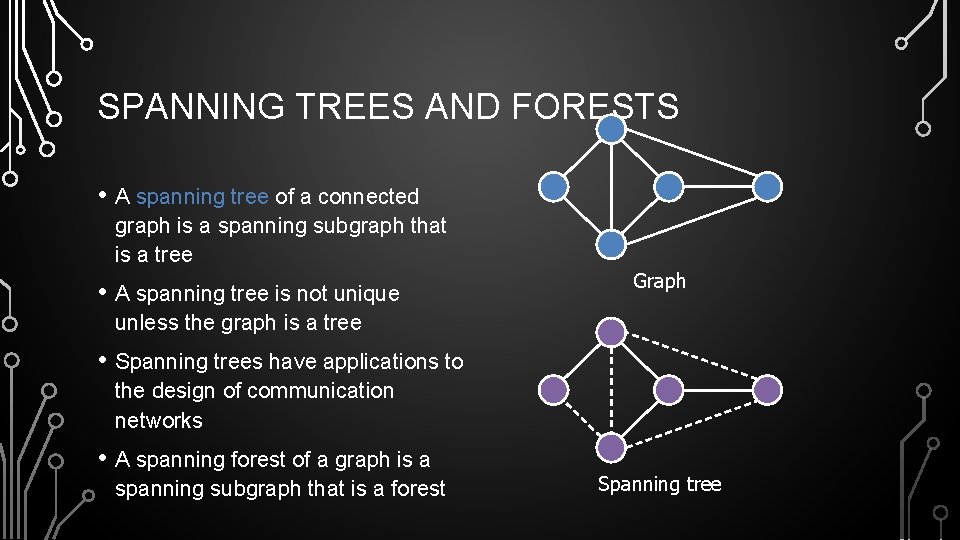
SPANNING TREES AND FORESTS • A spanning tree of a connected graph is a spanning subgraph that is a tree • A spanning tree is not unique Graph unless the graph is a tree • Spanning trees have applications to the design of communication networks • A spanning forest of a graph is a spanning subgraph that is a forest Spanning tree

GRAPH ADT • •

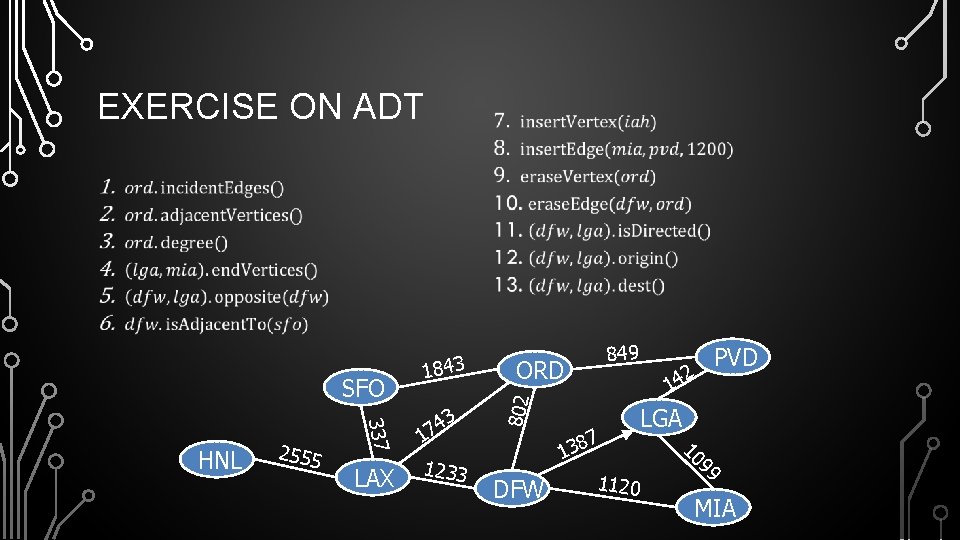
EXERCISE ON ADT • • 337 HNL 2555 LAX 3 4 17 1233 849 ORD 802 SFO 1843 DFW 14 7 8 3 1 1120 PVD 2 LGA 10 99 MIA

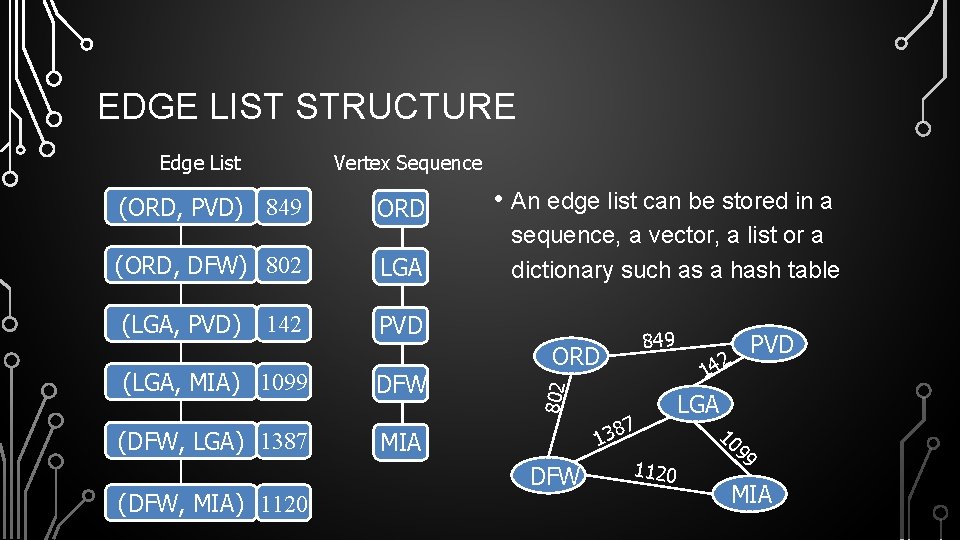
EDGE LIST STRUCTURE Vertex Sequence (ORD, PVD) 849 ORD (ORD, DFW) 802 LGA (LGA, PVD) PVD 142 (LGA, MIA) 1099 (DFW, LGA) 1387 (DFW, MIA) 1120 DFW • An edge list can be stored in a sequence, a vector, a list or a dictionary such as a hash table 849 ORD 14 802 Edge List 7 138 MIA DFW 1120 PVD 2 LGA 10 99 MIA

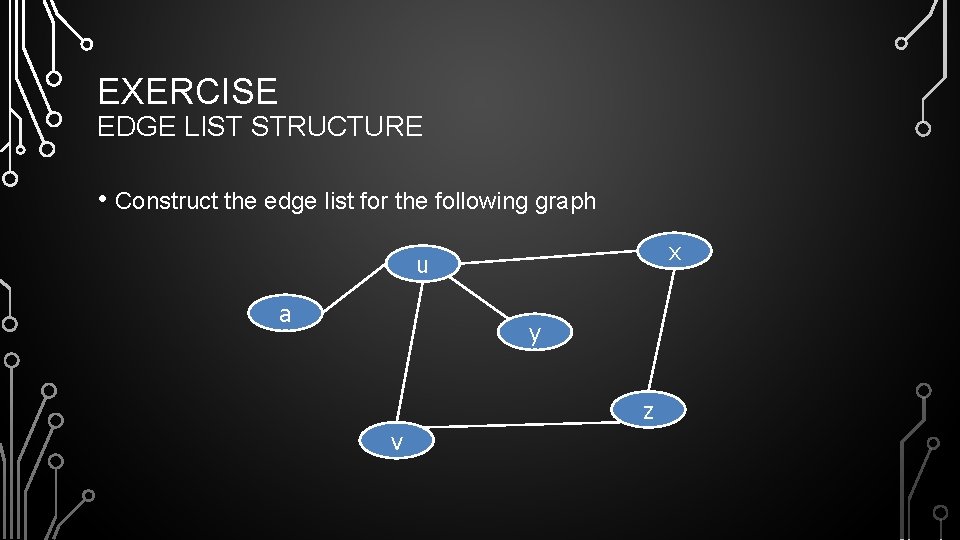
EXERCISE EDGE LIST STRUCTURE • Construct the edge list for the following graph x u a y z v

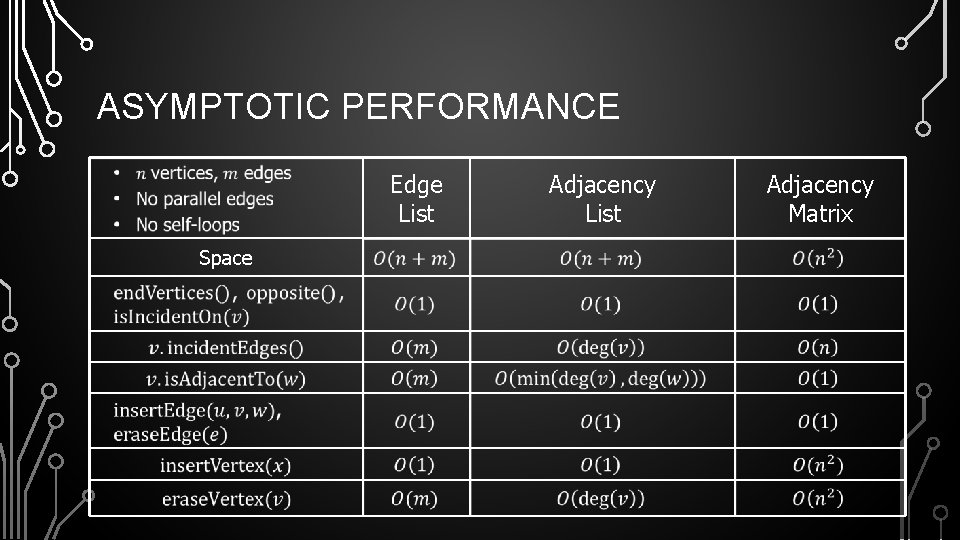
ASYMPTOTIC PERFORMANCE EDGE LIST STRUCTURE Edge List Weight Directed (ORD, PVD) Space ? ? ? Vertex Sequence Degree 849 False ORD 2 (ORD, DFW) 802 False LGA 3 (LGA, PVD) 142 False PVD 2 (LGA, MIA) 1099 False DFW 3 (DFW, LGA) 1387 False MIA 2 (DFW, MIA) 1120 False

ASYMPTOTIC PERFORMANCE EDGE LIST STRUCTURE Edge List Weight Directed (ORD, PVD) Space Vertex Sequence Degree 849 False ORD 2 (ORD, DFW) 802 False LGA 3 (LGA, PVD) 142 False PVD 2 (LGA, MIA) 1099 False DFW 3 (DFW, LGA) 1387 False MIA 2 (DFW, MIA) 1120 False

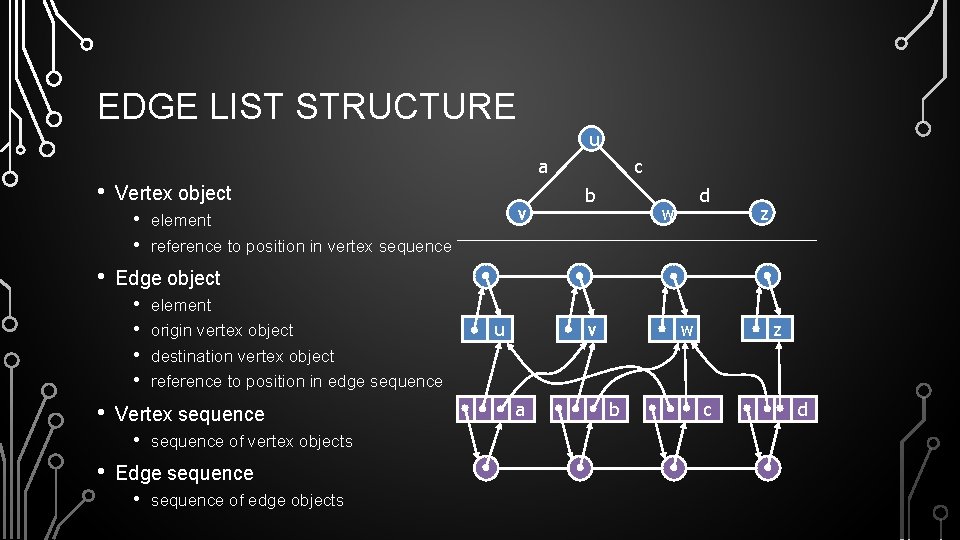
EDGE LIST STRUCTURE u a • Vertex object • • • element origin vertex object destination vertex object reference to position in edge sequence Vertex sequence • • b d w z Edge object • • • v element reference to position in vertex sequence c sequence of vertex objects Edge sequence • sequence of edge objects u a z w v b c d

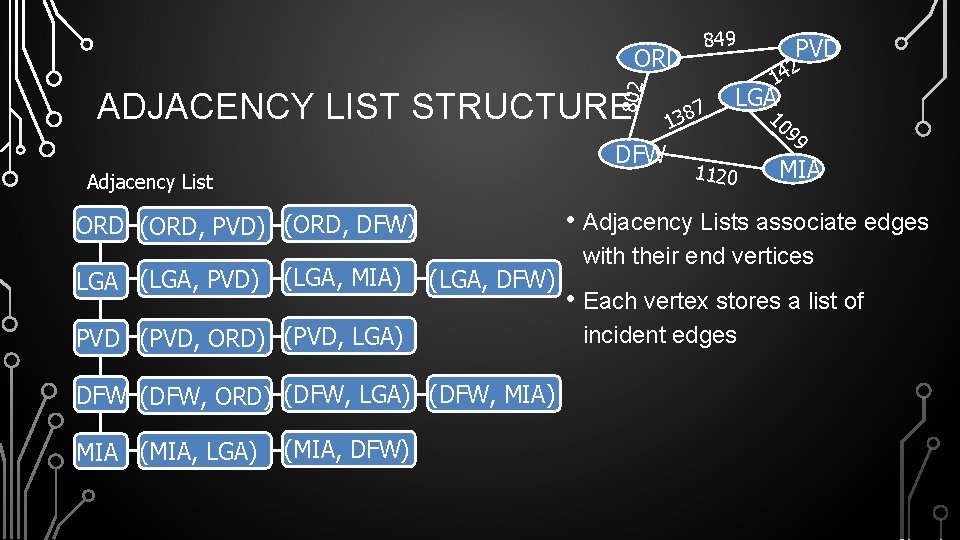
802 ORD ADJACENCY LIST STRUCTURE DFW Adjacency List (LGA, MIA) (LGA, DFW) PVD (PVD, ORD) (PVD, LGA) DFW (DFW, ORD) (DFW, LGA) (DFW, MIA) MIA (MIA, LGA) (MIA, DFW) 14 387 PVD 2 LGA 1120 10 99 MIA • Adjacency Lists associate edges ORD (ORD, PVD) (ORD, DFW) LGA (LGA, PVD) 1 849 with their end vertices • Each vertex stores a list of incident edges

EXERCISE ADJACENCY LIST STRUCTURE • Construct the adjacency list for the following graph x u a y z v

ASYMPTOTIC PERFORMANCE ADJACENCY LIST STRUCTURE Adjacency List ORD (ORD, PVD) (ORD, DFW) Space ? LGA (LGA, PVD) (LGA, MIA) (LGA, DFW) PVD (PVD, ORD) (PVD, LGA) ? ? DFW (DFW, ORD) (DFW, LGA) (DFW, MIA) MIA (MIA, LGA) (MIA, DFW)

ASYMPTOTIC PERFORMANCE ADJACENCY LIST STRUCTURE Adjacency List ORD (ORD, PVD) (ORD, DFW) Space LGA (LGA, PVD) (LGA, MIA) (LGA, DFW) PVD (PVD, ORD) (PVD, LGA) DFW (DFW, ORD) (DFW, LGA) (DFW, MIA) MIA (MIA, LGA) (MIA, DFW)

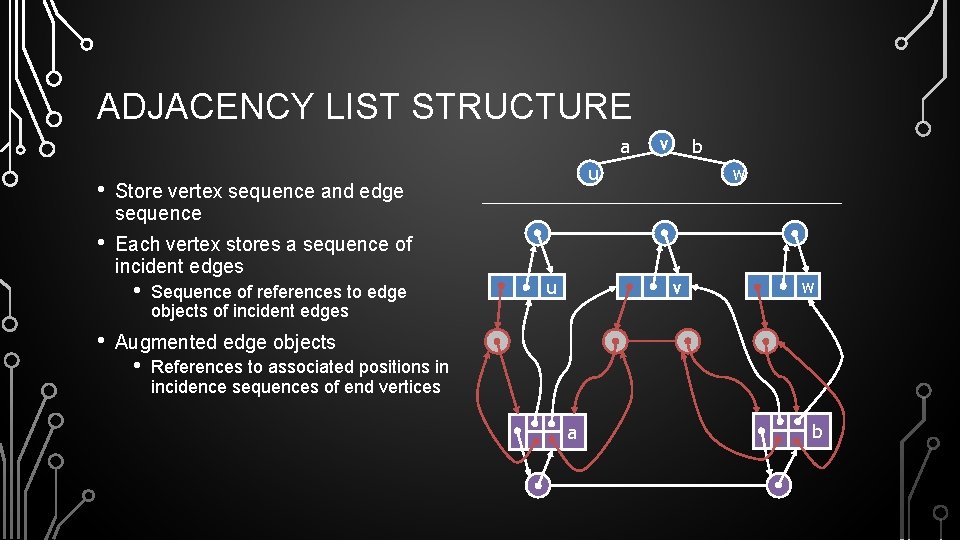
ADJACENCY LIST STRUCTURE a • Store vertex sequence and edge sequence • Each vertex stores a sequence of incident edges • • Sequence of references to edge objects of incident edges v b u u w v w Augmented edge objects • References to associated positions in incidence sequences of end vertices a b

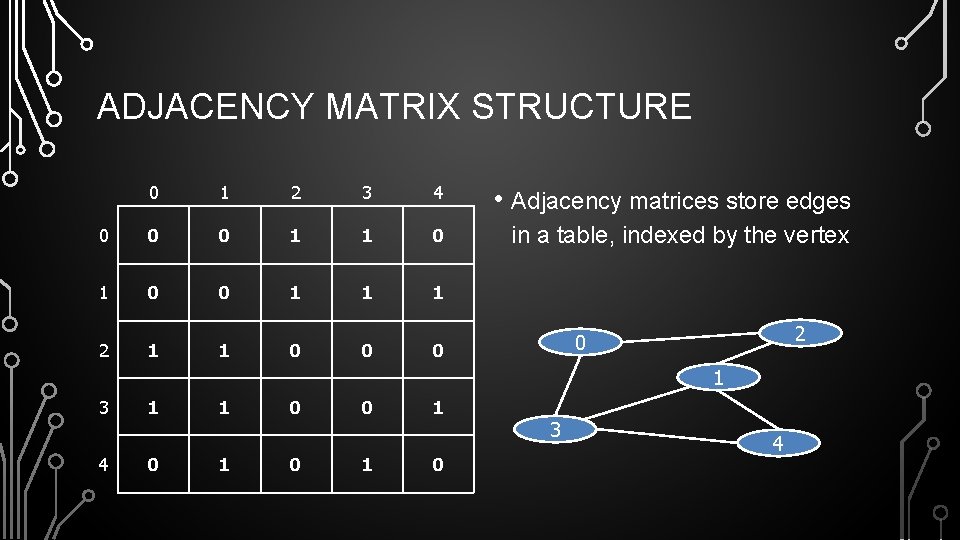
ADJACENCY MATRIX STRUCTURE 0 1 2 3 4 • Adjacency matrices store edges 0 0 0 1 1 0 in a table, indexed by the vertex 1 0 0 1 1 1 2 1 1 0 0 2 0 0 1 3 4 1 0 1 1 0 0 0 1 1 0 3 4

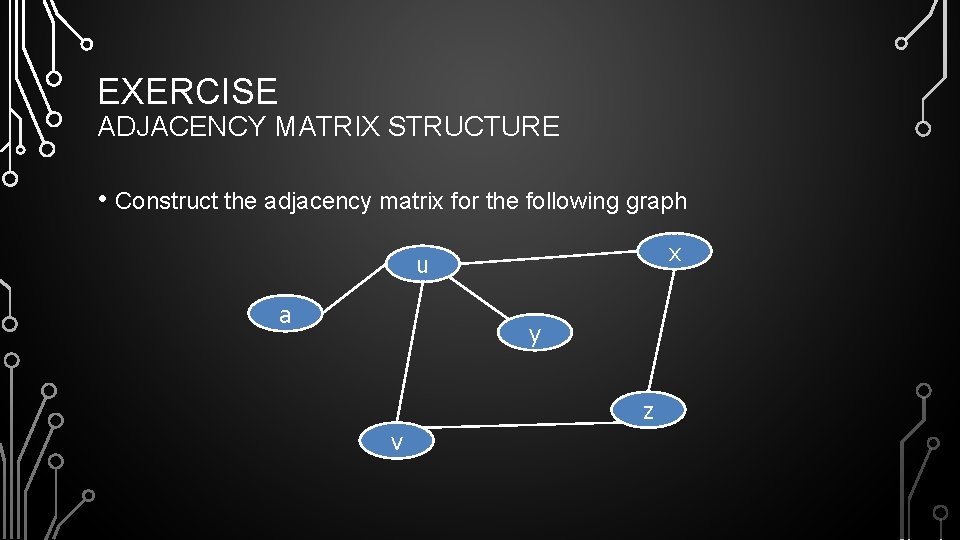
EXERCISE ADJACENCY MATRIX STRUCTURE • Construct the adjacency matrix for the following graph x u a y z v

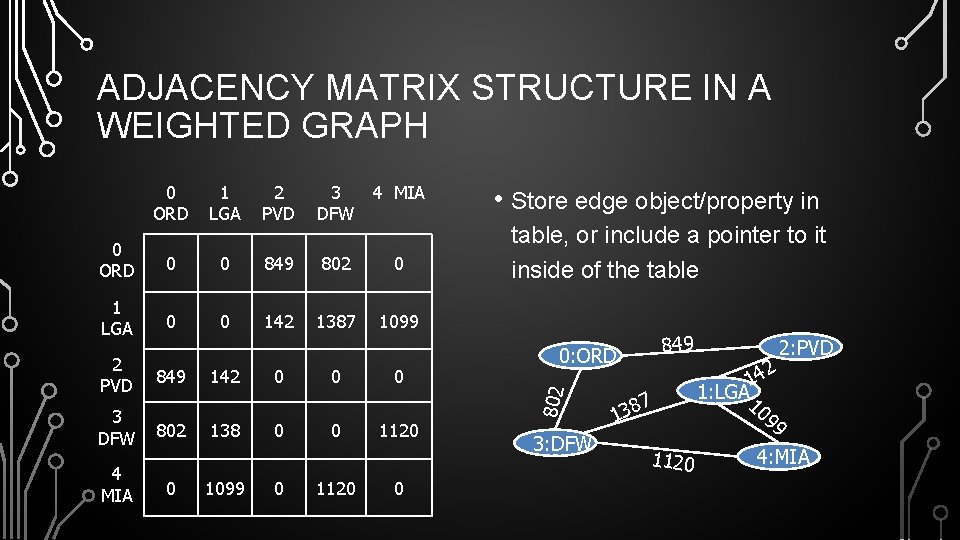
ADJACENCY MATRIX STRUCTURE IN A WEIGHTED GRAPH 0 ORD 1 LGA 2 PVD 3 4 MIA DFW 0 ORD 0 0 849 802 0 1 LGA 0 0 142 1387 1099 849 3 DFW 802 4 MIA 0 142 0 0 0 table, or include a pointer to it inside of the table 138 1099 0 0 0 1120 0 849 0: ORD 802 2 PVD • Store edge object/property in 3: DFW 7 138 1120 2 14 1: LGA 1 09 9 2: PVD 4: MIA

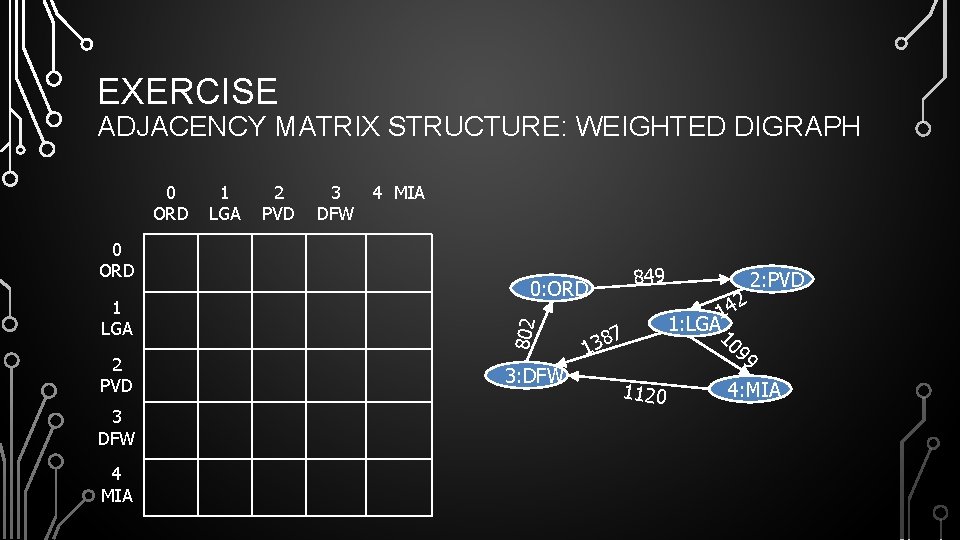
EXERCISE ADJACENCY MATRIX STRUCTURE: WEIGHTED DIGRAPH 0 ORD 1 LGA 2 PVD 3 DFW 4 MIA 1 LGA 2 PVD 3 4 MIA DFW 849 0: ORD 802 0 ORD 3: DFW 7 138 1120 2 14 1: LGA 1 09 9 2: PVD 4: MIA

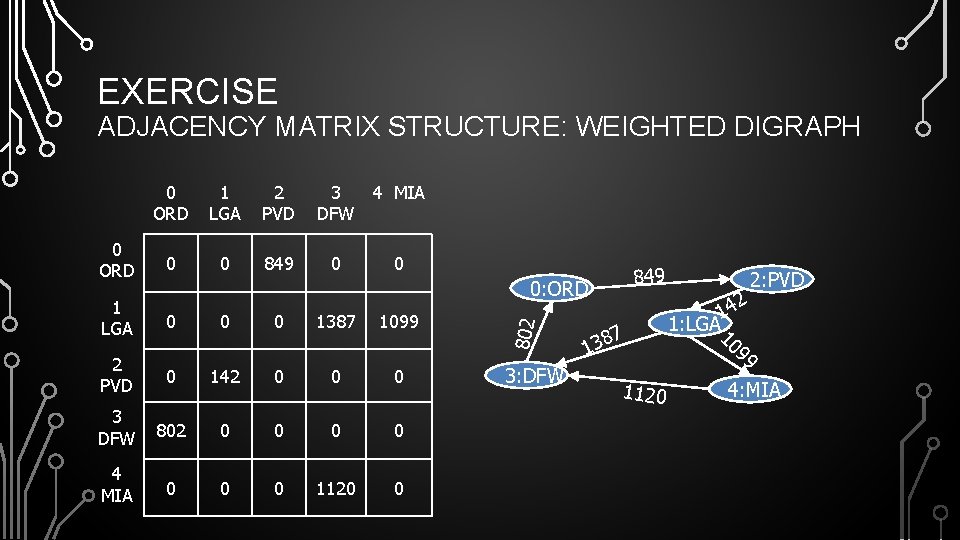
EXERCISE ADJACENCY MATRIX STRUCTURE: WEIGHTED DIGRAPH 1 LGA 2 PVD 0 0 849 3 4 MIA DFW 0 0 849 0: ORD 1 LGA 0 0 0 1387 1099 2 PVD 0 142 0 0 0 3 DFW 802 0 0 4 MIA 0 0 0 1120 0 802 0 ORD 3: DFW 7 138 1120 2 14 1: LGA 1 09 9 2: PVD 4: MIA

ASYMPTOTIC PERFORMANCE OF ADJACENCY MATRIX STRUCTURE Adjacency Matrix Space 0 1 2 3 4 0 0 0 1 1 1 2 1 1 0 0 0 ? 3 1 1 0 0 1 ? 4 0 1 0 ? ? ?

ASYMPTOTIC PERFORMANCE OF ADJACENCY MATRIX STRUCTURE Adjacency Matrix Space 0 1 2 3 4 0 0 0 1 1 1 2 1 1 0 0 0 3 1 1 0 0 1 4 0 1 0

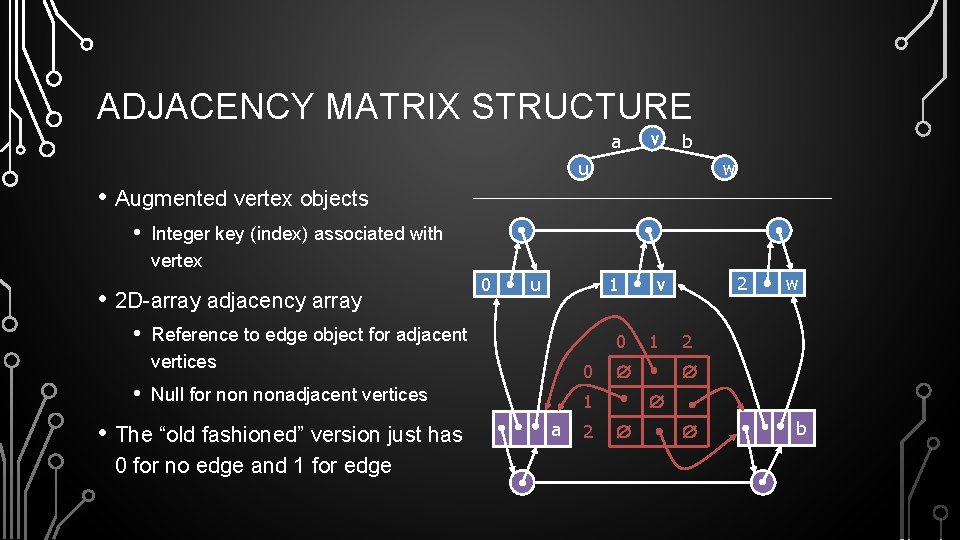
ADJACENCY MATRIX STRUCTURE a v b u w • Augmented vertex objects • Integer key (index) associated with vertex • 2 D-array adjacency array • • 0 u 1 Reference to edge object for adjacent vertices 0 0 Null for nonadjacent vertices • The “old fashioned” version just has 0 for no edge and 1 for edge 2 1 w 2 1 a 2 v b

ASYMPTOTIC PERFORMANCE Edge List Space Adjacency List Adjacency Matrix

A DEPTH-FIRST SEARCH B D C E

DEPTH-FIRST SEARCH • •

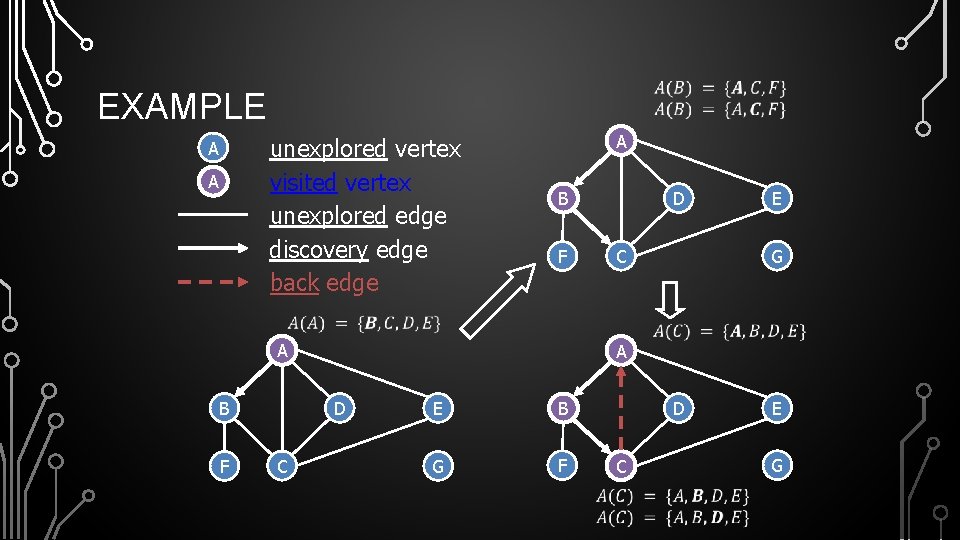
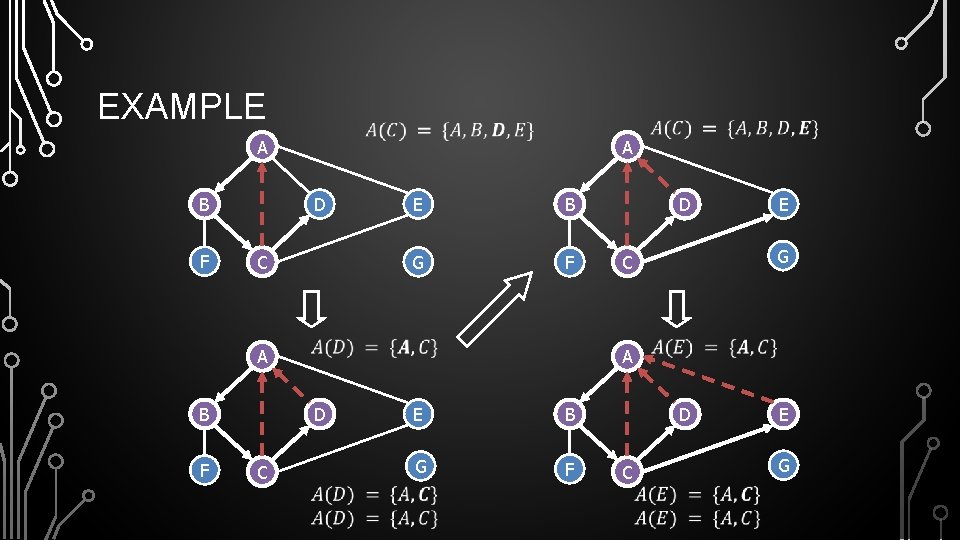
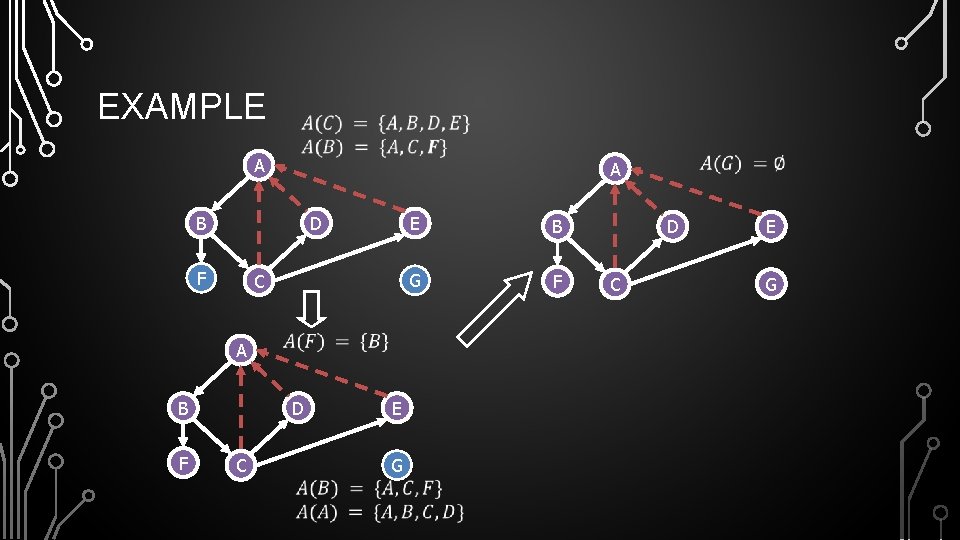
EXAMPLE unexplored vertex visited vertex unexplored edge discovery edge back edge A A A B F E G C A D C D E B G F D C E G

EXAMPLE A B F A D C E B G F A B F E G C A D C D E B G F D C E G

EXAMPLE A A B D F C A B F D C E G E B G F D C E G

DFS AND MAZE TRAVERSAL • The DFS algorithm is similar to a classic strategy for exploring a maze • We mark each intersection, corner and dead end (vertex) visited • We mark each corridor (edge) traversed • We keep track of the path back to the entrance (start vertex) by means of a rope (recursion stack)

DFS ALGORITHM • •

EXERCISE DFS ALGORITHM • Perform DFS of the following graph, start from vertex A • • • Assume adjacent edges are processed in alphabetical order Number vertices in the order they are visited Label edges as discovery or back edges A B C E D F

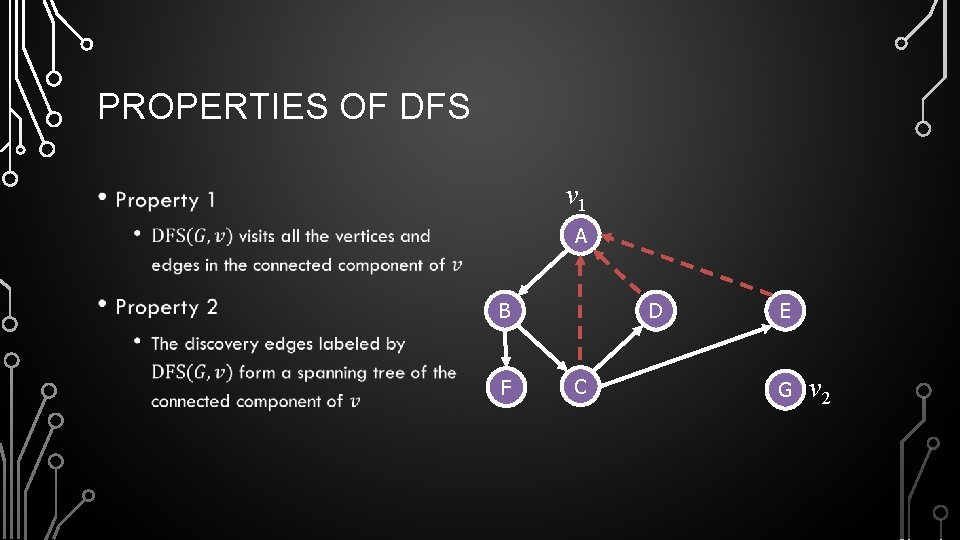
PROPERTIES OF DFS v 1 • A B F D C E G v 2

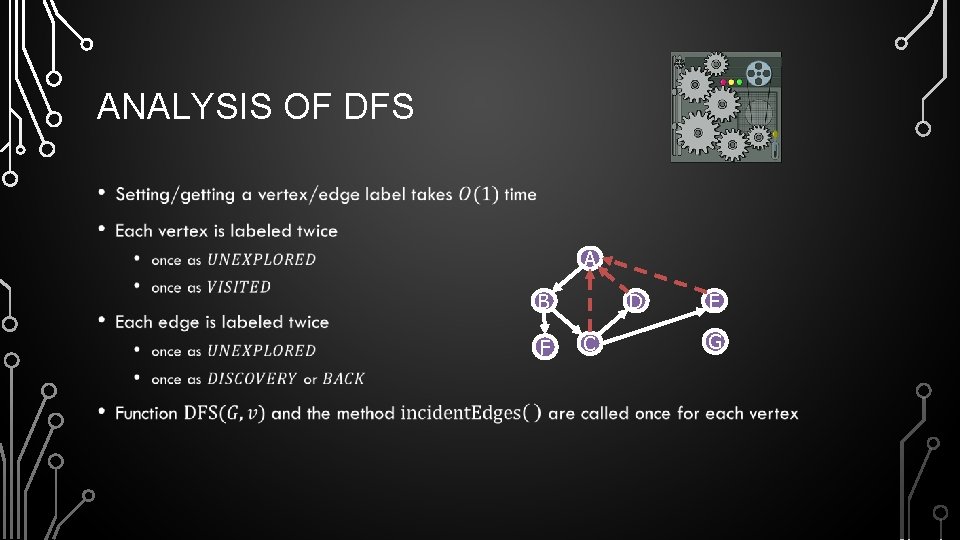
ANALYSIS OF DFS • A B F D C E G

ANALYSIS OF DFS • •

APPLICATION PATH FINDING • •

APPLICATION CYCLE FINDING • •

L 0 L 1 BREADTH-FIRST SEARCH A B L 2 C E D F

BREADTH-FIRST SEARCH • •

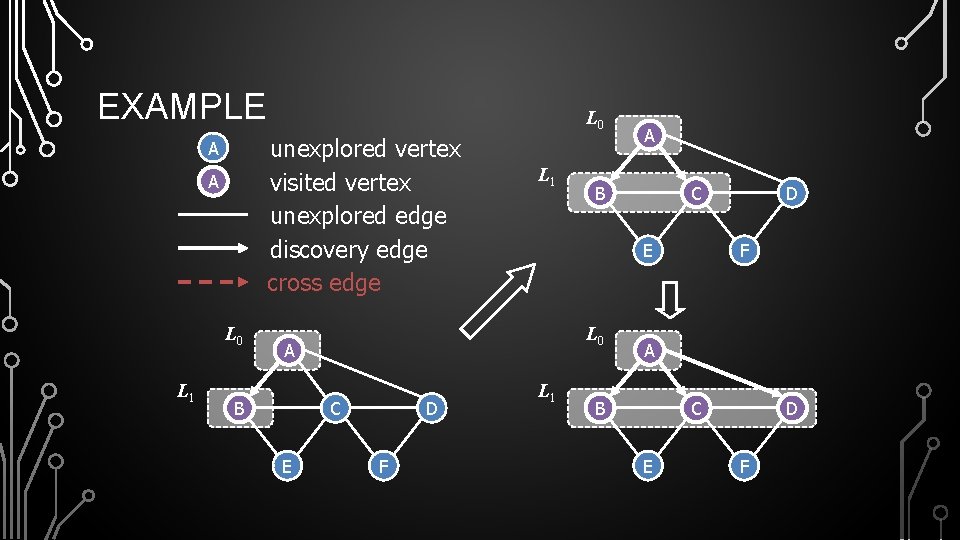
EXAMPLE unexplored vertex visited vertex unexplored edge discovery edge cross edge A A L 0 L 1 L 0 C E B D F C E A B A L 1 D F A B C E D F

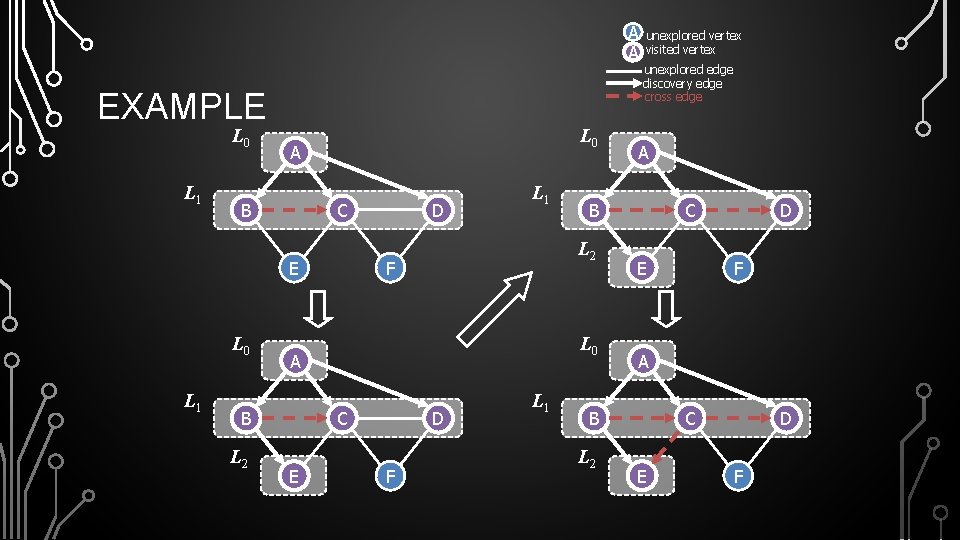
A A EXAMPLE L 0 L 1 L 0 A B C E L 0 L 1 F L 0 C E D F L 1 unexplored edge discovery edge cross edge A B L 2 D L 1 unexplored vertex visited vertex C E F A B L 2 D C E D F

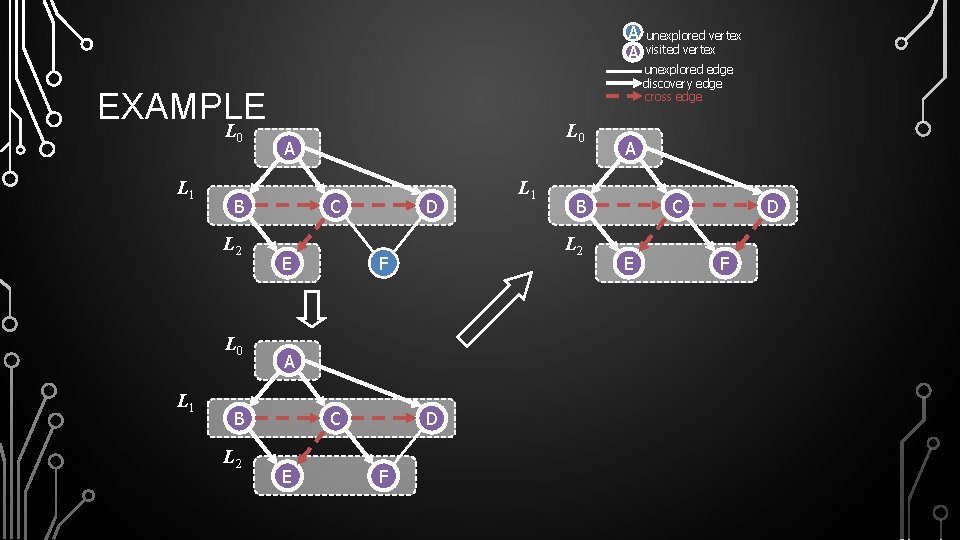
A A EXAMPLE L 0 L 1 A B L 2 C E D F L 1 unexplored edge discovery edge cross edge A B L 2 L 0 unexplored vertex visited vertex C E D F

BFS ALGORITHM • •

EXERCISE BFS ALGORITHM • Perform BFS of the following graph, start from vertex A • • • Assume adjacent edges are processed in alphabetical order Number vertices in the order they are visited and note the level they are in Label edges as discovery or cross edges A B C E D F

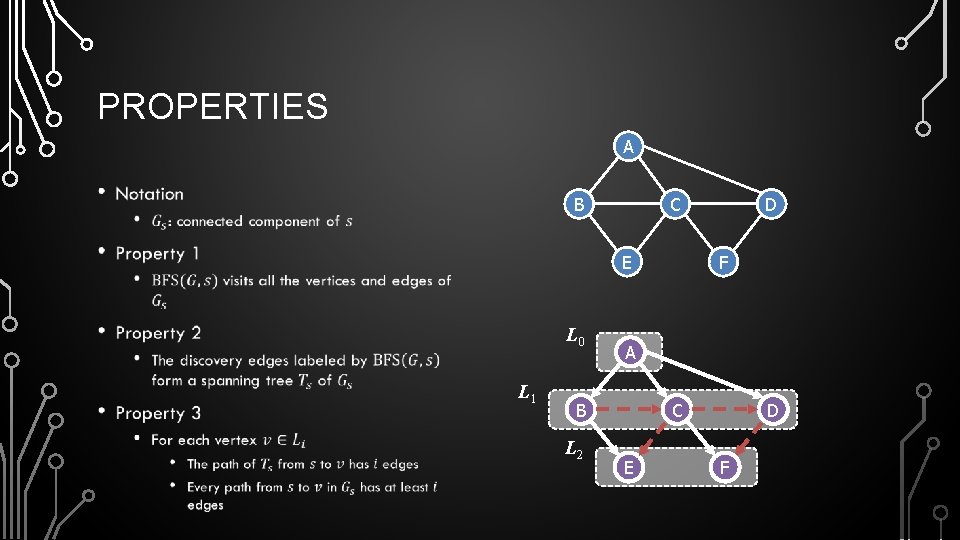
PROPERTIES A • B C E L 0 L 1 F A B L 2 D C E D F

ANALYSIS •

ANALYSIS OF BFS • •

APPLICATIONS •

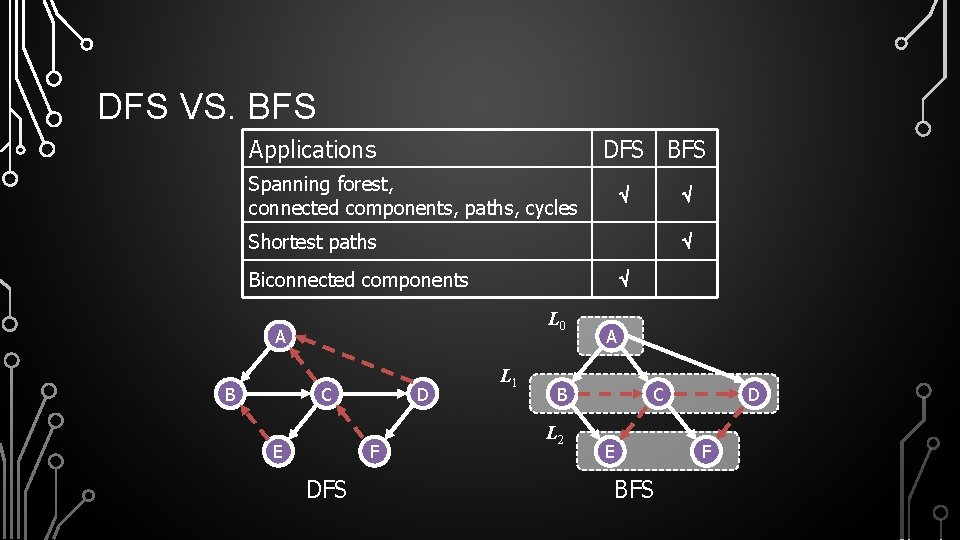
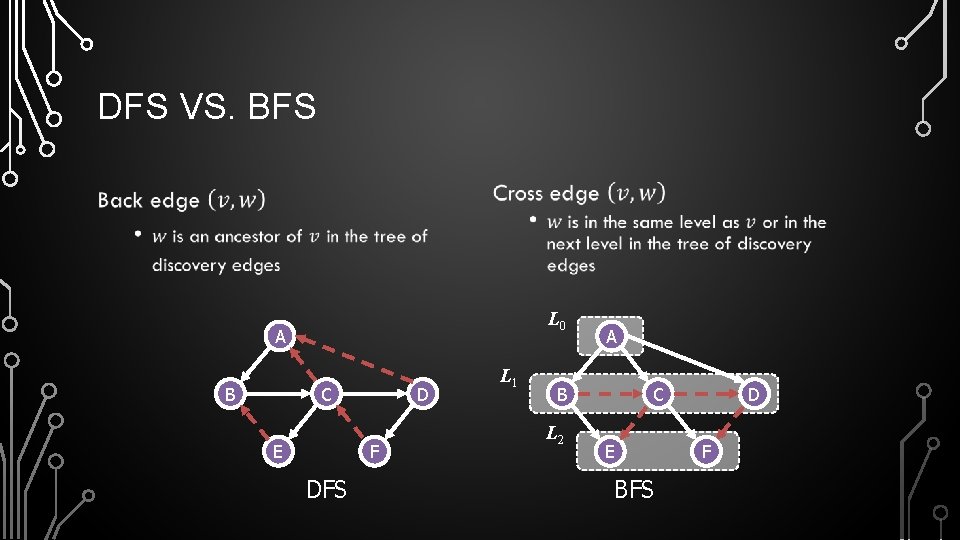
DFS VS. BFS Applications DFS BFS Spanning forest, connected components, paths, cycles Shortest paths Biconnected components L 0 A B C E D F DFS L 1 A B L 2 C E BFS D F

DFS VS. BFS • • L 0 A B C E D F DFS L 1 A B L 2 C E BFS D F