Graph Algorithm Recap n A topological sort of

Recap n A topological sort of a DAG G is a linear ordering of

Algorithm Example n find source nodes (indegree = 0) n if there is no

Degrees Summary n number of edges connected to a vertex n for undirected graphs

Conectivity n connected n n there exists a path between every pair of vertices

Cycles n n A tree does not have a cycle Eulerian cycle n n

Spanning Tree n Given a graph G = (V, E) and tree T =

Minimal Spanning Tree n n sum of edge weights is minimal if there is

1. Vertex D has been chosen as a starting point ① ② Vertices A,

2. The next vertex chosen is the vertex nearest to either D or A.

7. The finally obtained minimum spanning tree the total weight is 39

Dijkstra’s Algorithm n Goal: Find the shortest path from s to t 24 2

All Pairs Shortest Paths n Use Dijkstra’s method for all the vertices n n

Network Flow n Think edges as pipes n what’s the maximum flow from node

Slides: 20

Download presentation

Graph Algorithm

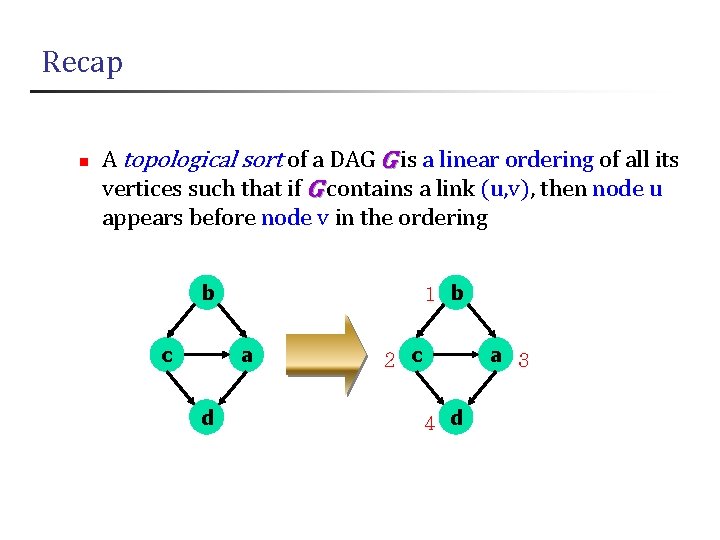
Recap n A topological sort of a DAG G is a linear ordering of all its vertices such that if G contains a link (u, v), then node u appears before node v in the ordering b c 1 b a d 2 c a 3 4 d

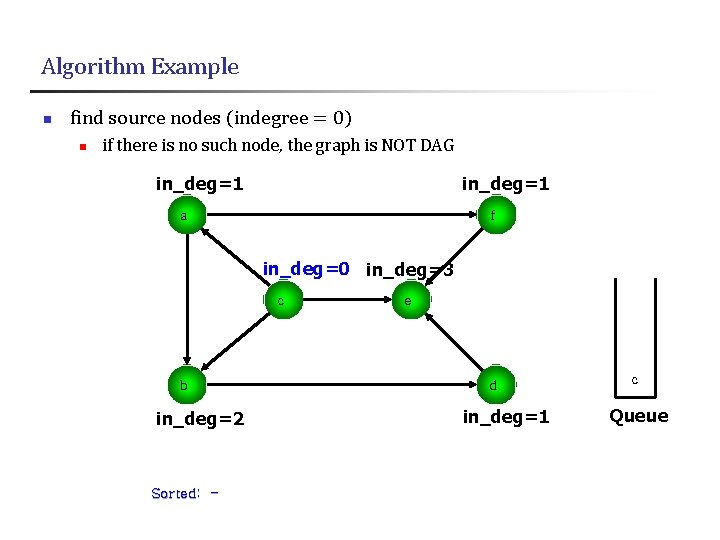
Algorithm Example n find source nodes (indegree = 0) n if there is no such node, the graph is NOT DAG in_deg=1 a f in_deg=0 in_deg=3 c b in_deg=2 Sorted: - e d in_deg=1 c Queue

Degrees Summary n number of edges connected to a vertex n for undirected graphs n n sum of all degrees = 2 X edges n the number of nodes with odd numbered degrees is even? for directed graph n sum of in-degree = sum of out-degree

Conectivity n connected n n there exists a path between every pair of vertices articulation vertex n n n deleting this vertex makes the graph disconnected a graph without any such vertex is biconnected deleting a bridge edge makes the graph disconnected

Cycles n n A tree does not have a cycle Eulerian cycle n n a tour that visits every edge exactly once Hamiltonian cycle (path) n a tour that visits every vertex exactly once

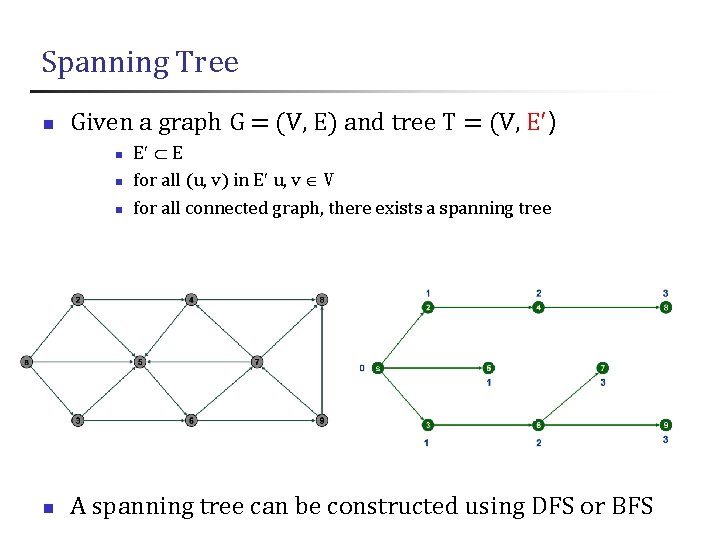
Spanning Tree n Given a graph G = (V, E) and tree T = (V, E ) n n E E for all (u, v) in E u, v V for all connected graph, there exists a spanning tree A spanning tree can be constructed using DFS or BFS

Minimal Spanning Tree n n sum of edge weights is minimal if there is no weight n n the number of edges is minimal why is it so important? n search space is minimal for most problems

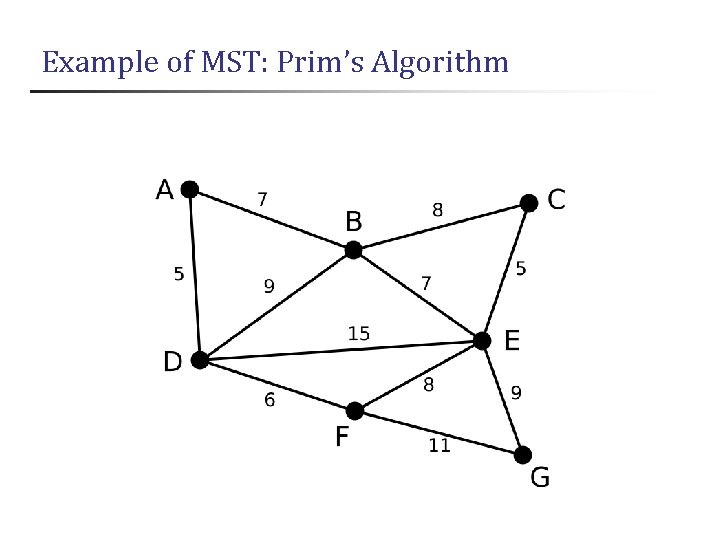
Example of MST: Prim’s Algorithm

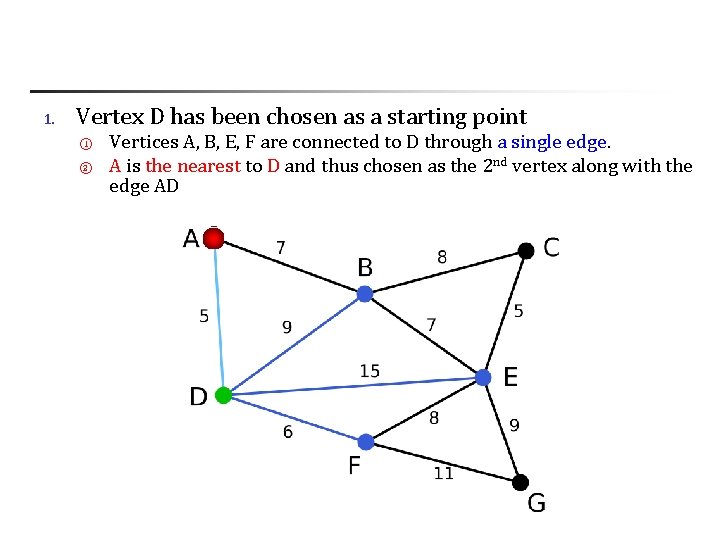
1. Vertex D has been chosen as a starting point ① ② Vertices A, B, E, F are connected to D through a single edge. A is the nearest to D and thus chosen as the 2 nd vertex along with the edge AD

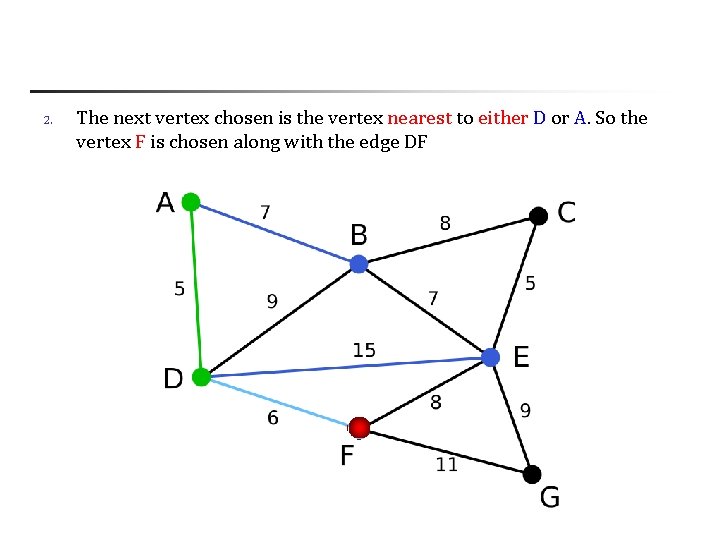
2. The next vertex chosen is the vertex nearest to either D or A. So the vertex F is chosen along with the edge DF

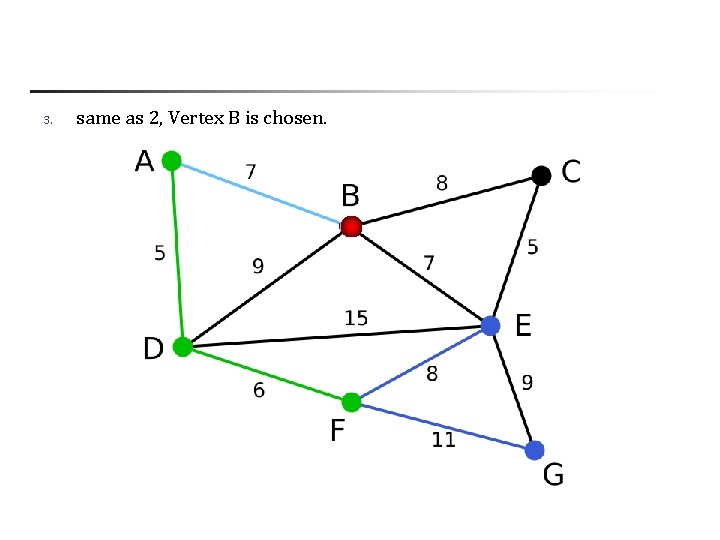
3. same as 2, Vertex B is chosen.

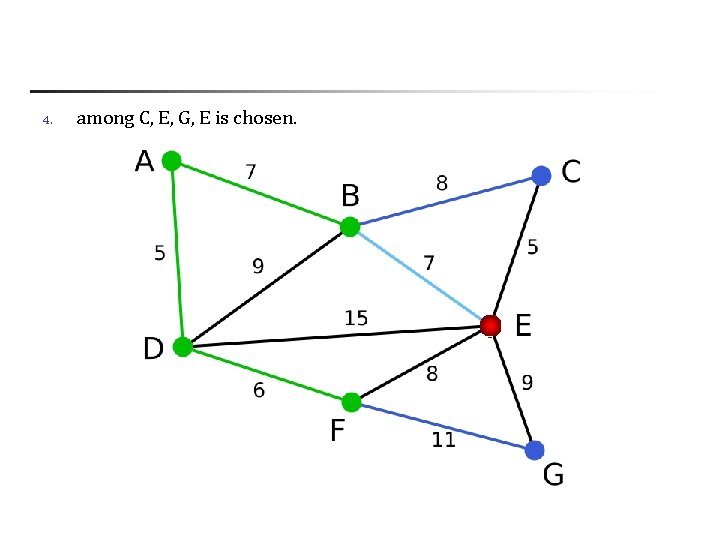
4. among C, E, G, E is chosen.

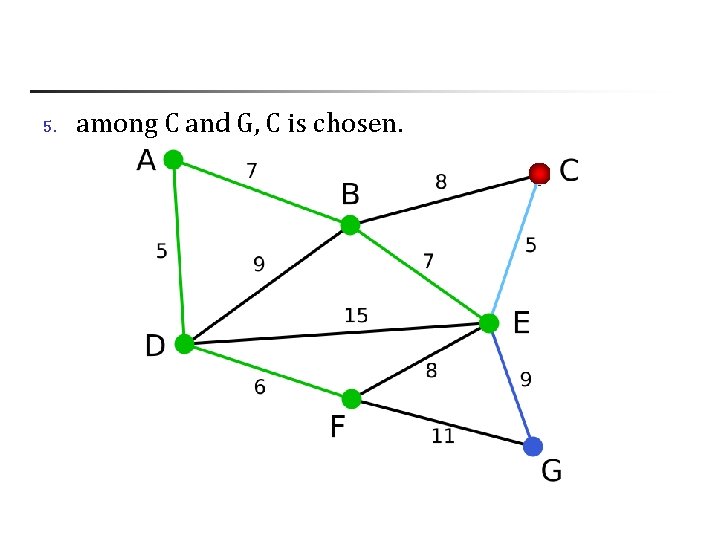
5. among C and G, C is chosen.

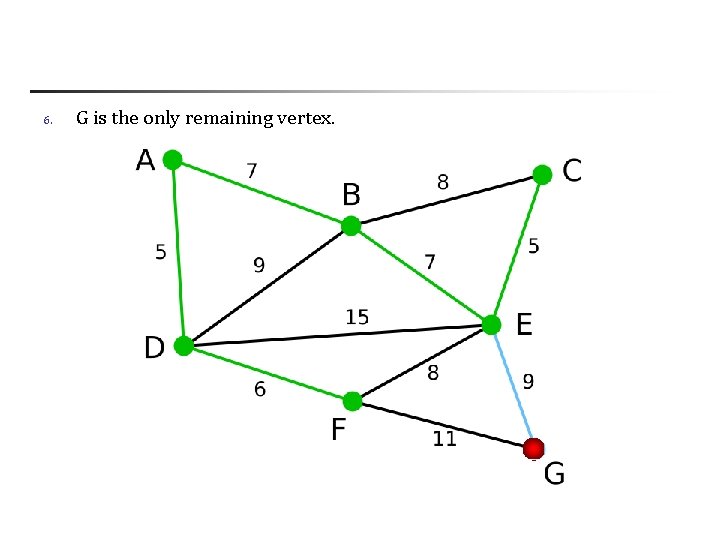
6. G is the only remaining vertex.

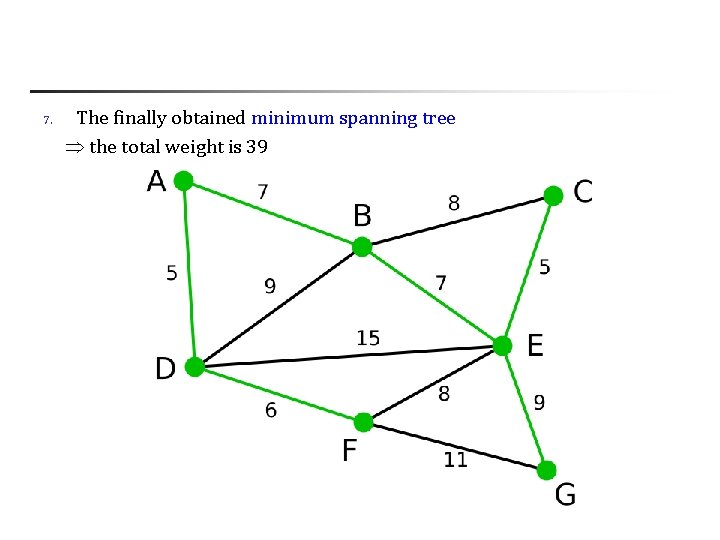
7. The finally obtained minimum spanning tree the total weight is 39

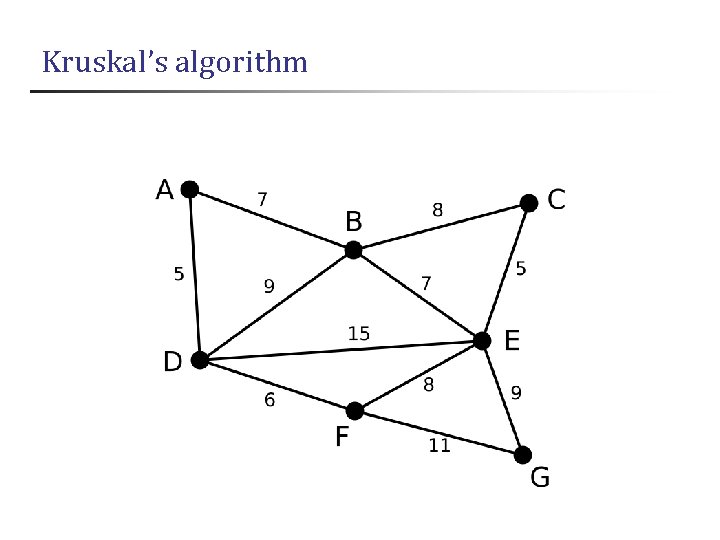
Kruskal’s algorithm

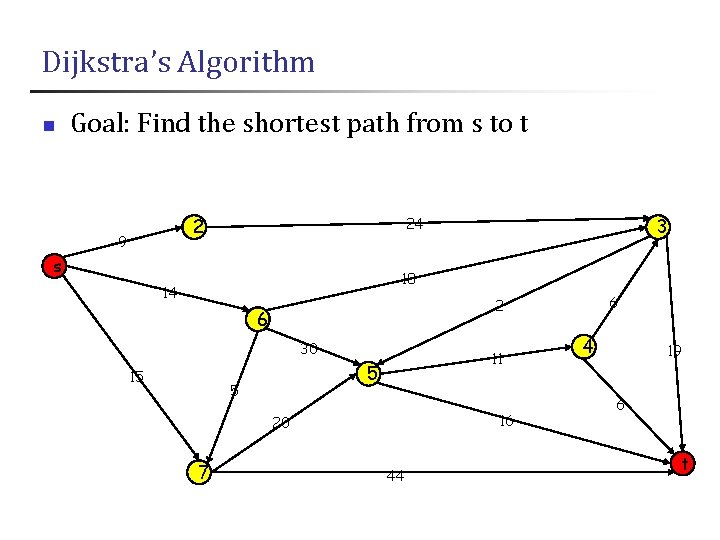
Dijkstra’s Algorithm n Goal: Find the shortest path from s to t 24 2 9 s 3 18 14 6 30 15 11 5 5 16 20 7 6 2 44 4 19 6 t

All Pairs Shortest Paths n Use Dijkstra’s method for all the vertices n n complexity? Floyd’s method n Given the adjacency matrix with vertices numbered (1. . n)

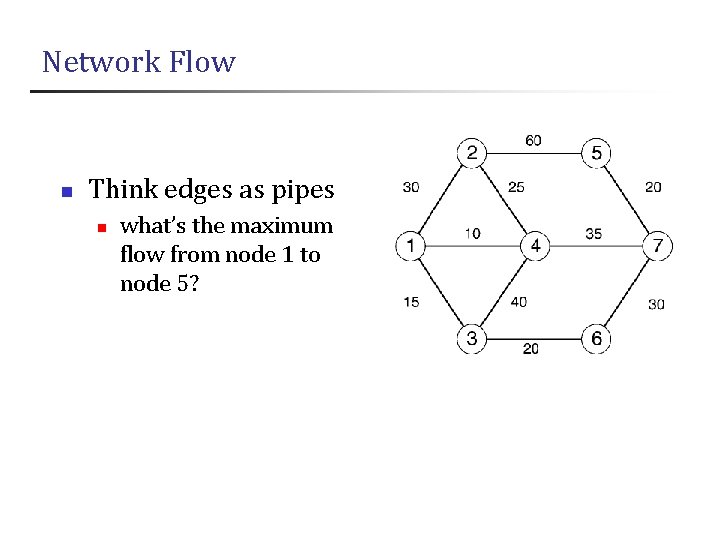
Network Flow n Think edges as pipes n what’s the maximum flow from node 1 to node 5?