Graph A graph G V E consists of

Graph • A graph G = (V, E) consists of V, a nonempty set of vertices (or nodes) and E, a set of edges. Each edge has either one or two vertices associated with it, called its endpoints. An edge is said to connect its endpoints. • A graph with an infinite vertex set is called an infinite graph • A graph with a finite vertex set is called a finite graph.

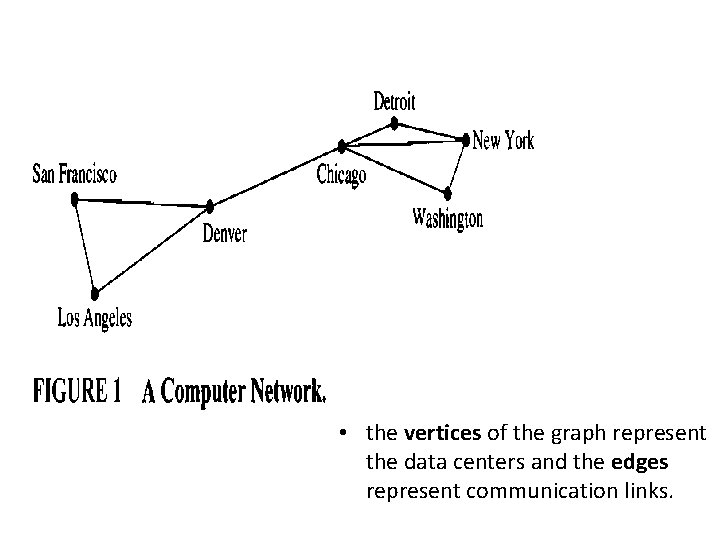
• the vertices of the graph represent the data centers and the edges represent communication links.

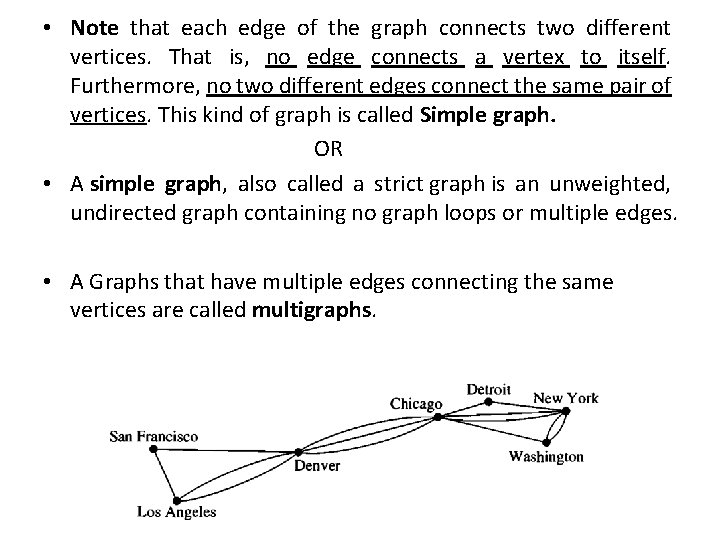
• Note that each edge of the graph connects two different vertices. That is, no edge connects a vertex to itself. Furthermore, no two different edges connect the same pair of vertices. This kind of graph is called Simple graph. OR • A simple graph, also called a strict graph is an unweighted, undirected graph containing no graph loops or multiple edges. • A Graphs that have multiple edges connecting the same vertices are called multigraphs.

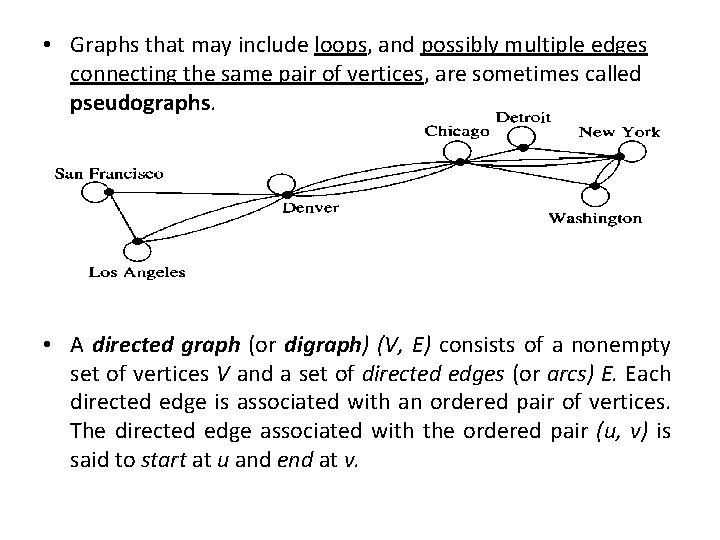
• Graphs that may include loops, and possibly multiple edges connecting the same pair of vertices, are sometimes called pseudographs. • A directed graph (or digraph) (V, E) consists of a nonempty set of vertices V and a set of directed edges (or arcs) E. Each directed edge is associated with an ordered pair of vertices. The directed edge associated with the ordered pair (u, v) is said to start at u and end at v.

• A directed graph may also contain directed edges that connect vertices u and v in both directions; that is, when a digraph contains an edge from u to v, it may also contain one or more edges from v to u. • When a directed graph has no loops and has no multiple directed edges, it is called a simple directed graph. Because a simple directed graph has at most one edge associated to each ordered pair of vertices (u, v)

• Directed graphs that may have multiple directed edges from a vertex to a second (possibly the same) vertex are to used model such networks. We called such graphs directed multigraphs. When there are m directed edges, each associated to an ordered pair of vertices (u, v), we say that (u, v) is an edge of multiplicity m. • A graph with both directed and undirected edges is called a mixed graph. For example, a mixed graph might be used to model a computer network containing links that operate in both directions and other links that operate only in one direction.

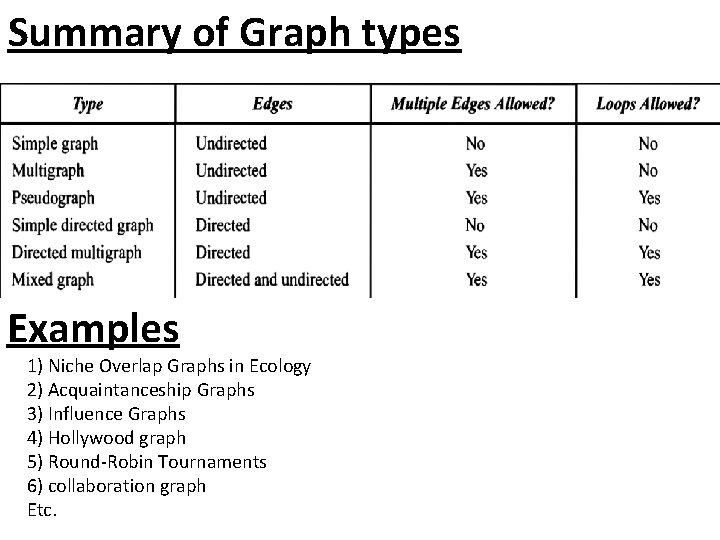
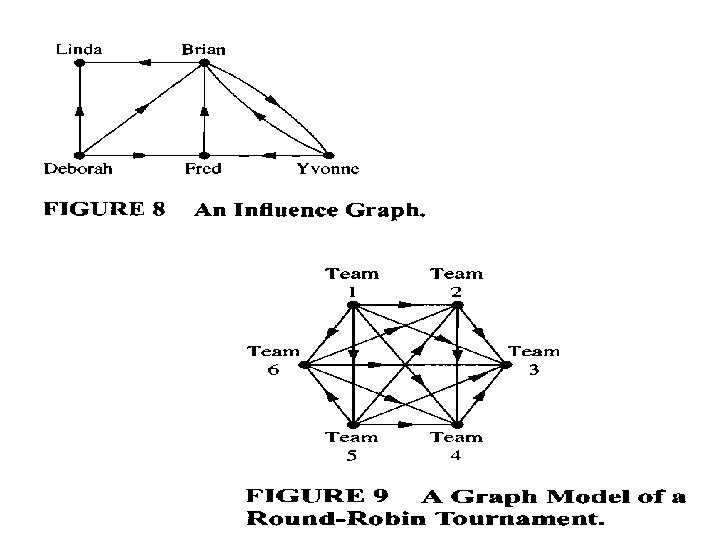
Summary of Graph types Examples 1) Niche Overlap Graphs in Ecology 2) Acquaintanceship Graphs 3) Influence Graphs 4) Hollywood graph 5) Round-Robin Tournaments 6) collaboration graph Etc.

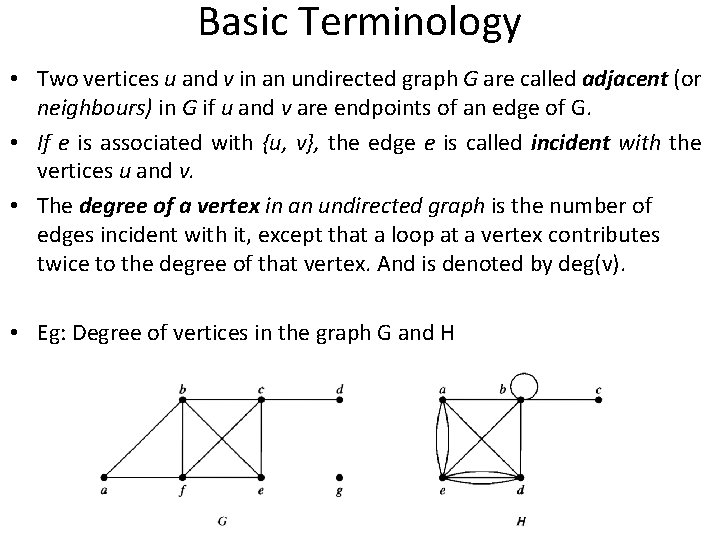
Basic Terminology • Two vertices u and v in an undirected graph G are called adjacent (or neighbours) in G if u and v are endpoints of an edge of G. • If e is associated with {u, v}, the edge e is called incident with the vertices u and v. • The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. And is denoted by deg(v). • Eg: Degree of vertices in the graph G and H

• In G, deg(a) = 2, deg(b) = deg(c) = deg(J) = 4, deg(d) = 1, deg(e) = 3, and deg(g) = 0. • In H, deg(a) = 4, deg(b) = deg(e) = 6, deg(c) = 1, and deg(d) =5. • A vertex of degree zero is called isolated(or isolated vertex is not adjacent to any vertex). • A vertex is pendant if and only if it has degree one( or a pendant vertex is adjacent to exactly one other vertex).

THE HANDSHAKING THEOREM(or Number of Edges in undirected graph) • Let G = (V, E) be an undirected graph with e edges. Then Q) How many edges are there in a graph with 10 vertices each of degree six? In an undirected graph, sum of degree is always even(can be verified using above equation) Q) An undirected graph has an even number of vertices of odd degree.

Terminology for directed graphs • When (u, v) is an edge of the graph G with directed edges, u is said to be adjacent to v and v is said to be adjacent from u. • The vertex u is called the initial vertex of(u, v), and v is called the terminal or end vertex of (u, v). Q) What is the initial and final vertex for a loop? • in-degree of a vertex v, denoted by deg- (v), is the number of edges with v as their terminal vertex. • The out-degree of v, denoted by deg +(v), is the number of edges with v as their initial vertex. (Note that a loop at a vertex contributes I to both the in-degree and the out-degree of this vertex. )

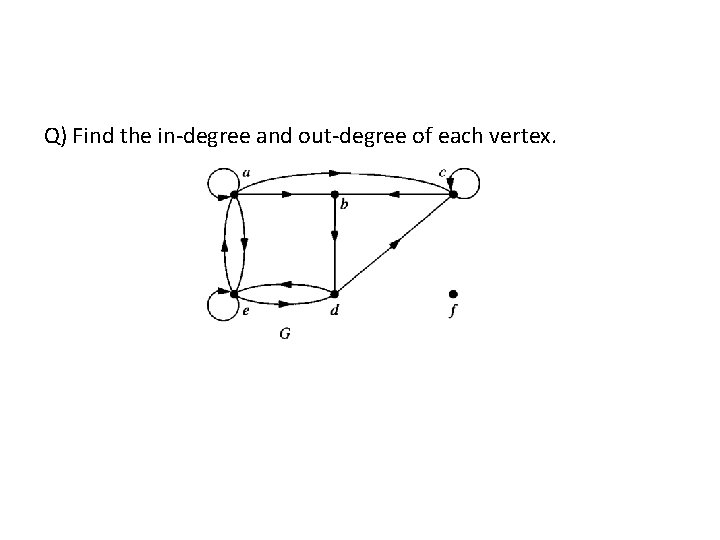
Q) Find the in-degree and out-degree of each vertex.

NOTE: • Because each edge has an initial vertex and a terminal vertex, the sum of the in-degrees and the sum of the out-degrees of all vertices in a graph with directed edges are the same. • Both of these sums are the number of edges in the graph.

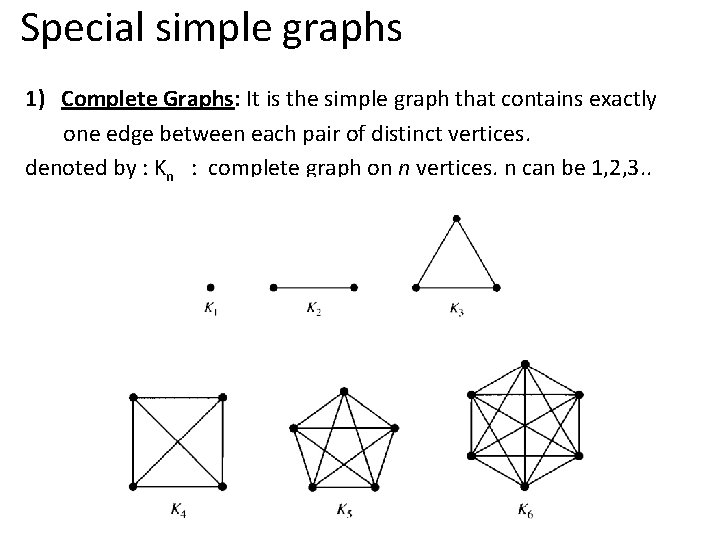
Special simple graphs 1) Complete Graphs: It is the simple graph that contains exactly one edge between each pair of distinct vertices. denoted by : Kn : complete graph on n vertices. n can be 1, 2, 3. .

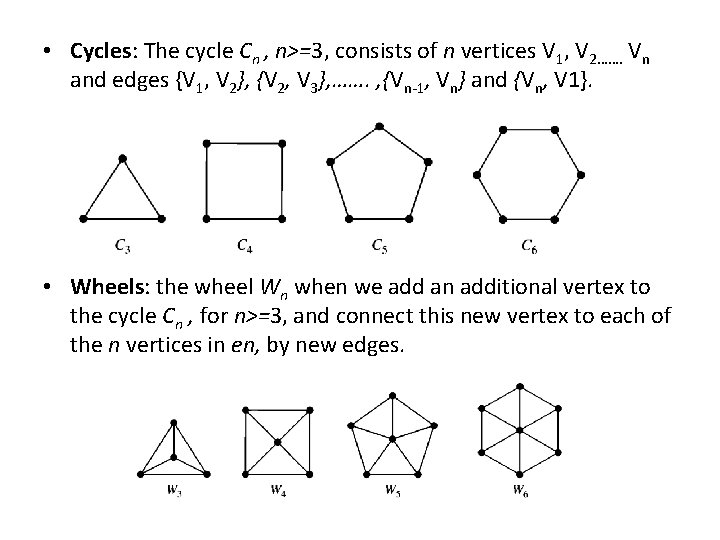
• Cycles: The cycle Cn , n>=3, consists of n vertices V 1, V 2……. Vn and edges {V 1, V 2}, {V 2, V 3}, ……. , {Vn-1, Vn} and {Vn, V 1}. • Wheels: the wheel Wn when we add an additional vertex to the cycle Cn , for n>=3, and connect this new vertex to each of the n vertices in en, by new edges.

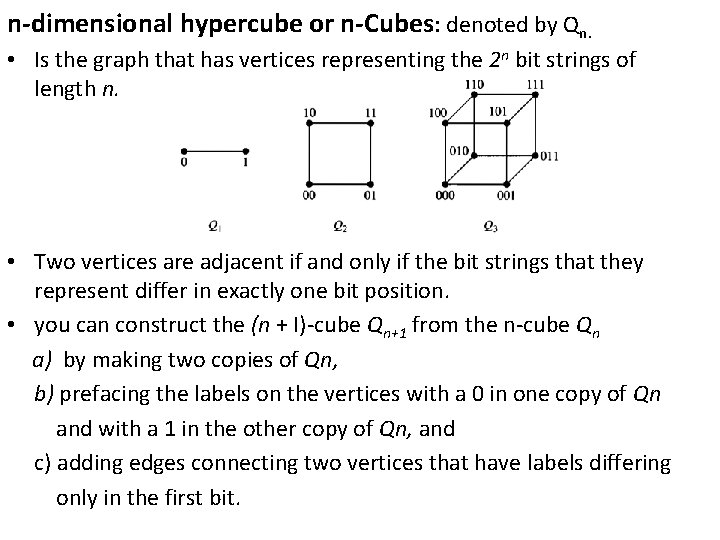
n-dimensional hypercube or n-Cubes: denoted by Qn. • Is the graph that has vertices representing the 2 n bit strings of length n. • Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position. • you can construct the (n + I)-cube Qn+1 from the n-cube Qn a) by making two copies of Qn, b) prefacing the labels on the vertices with a 0 in one copy of Qn and with a 1 in the other copy of Qn, and c) adding edges connecting two vertices that have labels differing only in the first bit.

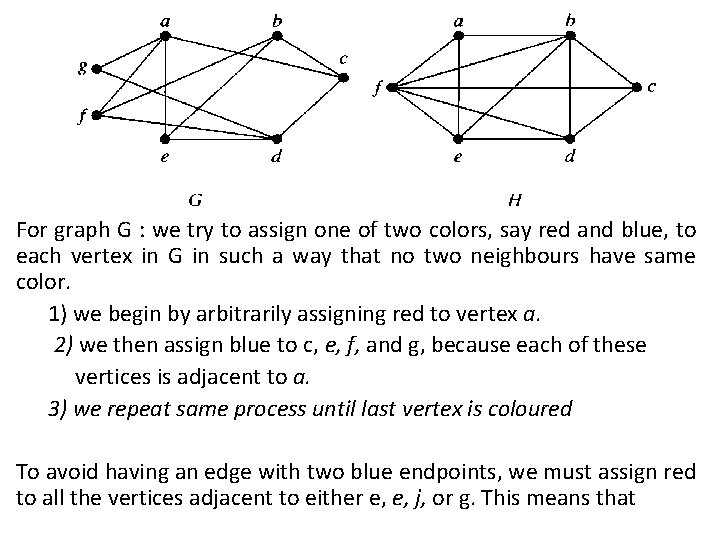
Bipartite Graphs • A simple graph G is called bipartite, if its vertex set V can be partitioned into two disjoint sets V 1 and V 2 such that every edge in the graph connects a vertex in V 1 and a vertex in V 2 (so that no edge in G connects either two vertices in V 1 or two vertices in V 2). OR • A simple graph is bipartite if and only if it is possible to assign one of two different colors to each vertex of the graph so that no two adjacent vertices are assigned the same color. Q) Which is bipartite graph C 6 or K 3 or none?

For graph G : we try to assign one of two colors, say red and blue, to each vertex in G in such a way that no two neighbours have same color. 1) we begin by arbitrarily assigning red to vertex a. 2) we then assign blue to c, e, f, and g, because each of these vertices is adjacent to a. 3) we repeat same process until last vertex is coloured To avoid having an edge with two blue endpoints, we must assign red to all the vertices adjacent to either e, e, j, or g. This means that

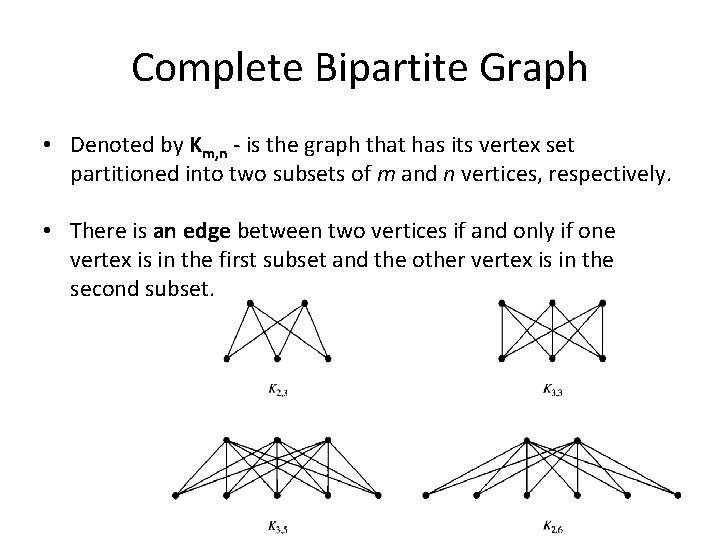
Complete Bipartite Graph • Denoted by Km, n - is the graph that has its vertex set partitioned into two subsets of m and n vertices, respectively. • There is an edge between two vertices if and only if one vertex is in the first subset and the other vertex is in the second subset.

Some Applications of Special Types of Graphs • Job Assignments: m employee and j different jobs that need to be done where m<=j (Each employee is trained to do one or more of these j jobs). • A matching in a simple graph is a subset of the set of edges of the graph such that no two edges are incident with the same vertex (A matching is a subset of edges such that if {s, t} and {u, v} are edges of the matching, then s, t, u, and v are distinct. ) • A maximal matching is a matching with the largest number of edges.

Other Applications • Local Area Networks (eg : - star, ring, hybrid topologies) • Interconnection networks for parallel computation

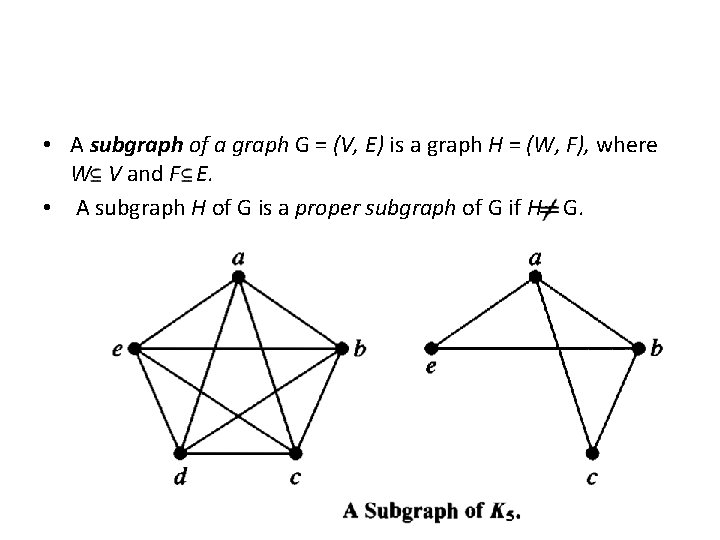
• A subgraph of a graph G = (V, E) is a graph H = (W, F), where W V and F E. • A subgraph H of G is a proper subgraph of G if H G.

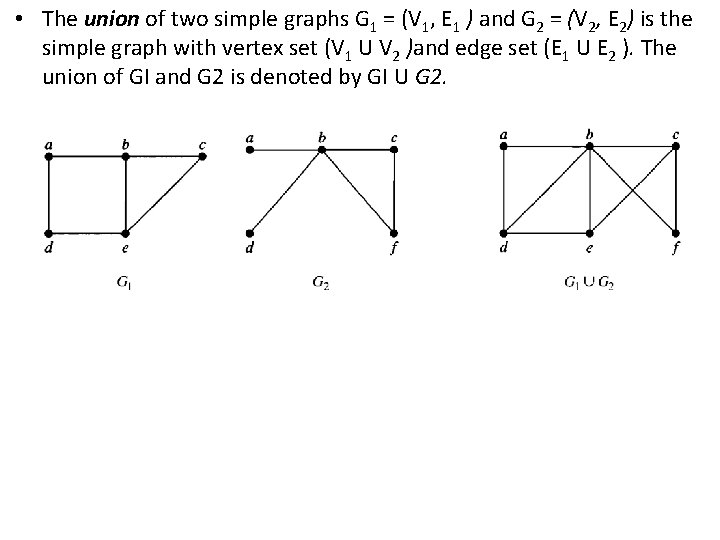
• The union of two simple graphs G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2) is the simple graph with vertex set (V 1 U V 2 )and edge set (E 1 U E 2 ). The union of GI and G 2 is denoted by GI U G 2.

Representing Graphs 1) Adjacency List 2) Adjacency Matrices Note: Adjacency matrix is a matrix between vertices as rows and columns Adjacency List is the list of vertices as terminals

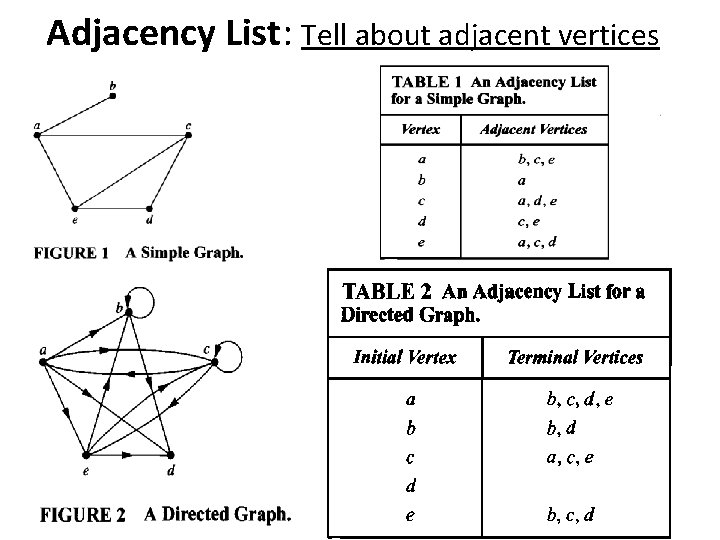
Adjacency List: Tell about adjacent vertices

Adjacency Matrices Suppose that G = (V, E) is a simple graph where IVI = n. Suppose that the vertices of G are listed arbitrarily as V 1, V 2, …, Vn. • The adjacency matrix A of G (AG) with respect to the listing of the vertices, is the n x n zero-one matrix with 1 as its (i, j)th entry when Vi and Vj are adjacent, and 0 as its (i, j)th entry when they are not adjacent OR • if its adjacency matrix is A = [aij], then aij = {1 If {Vi, Vj} is an edge of G, 0 otherwise. }

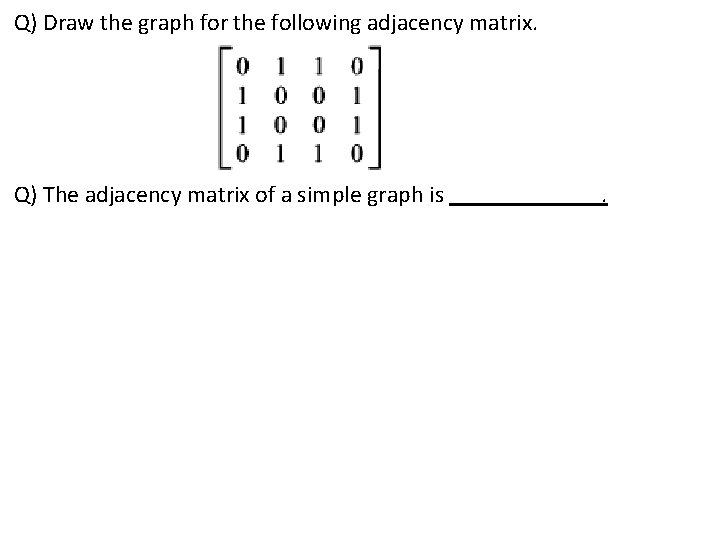
Q) Draw the graph for the following adjacency matrix. Q) The adjacency matrix of a simple graph is .

• When multiple edges are present, the adjacency matrix is no longer a zero--one matrix, because the (i, j)th entry of this matrix equals the number of edges that are associated to (ai, aj}. • All undirected graphs, including multigraphs and pseudographs, have symmetric adjacency matrices. • Q) Write the adjacency matrix to represent the pseudo the pseudograph. A Pseudograph

Q) The adjacency matrix for a directed graph (symmetric or not) • Adjacency matrices can also be used to represent directed multigraphs. Again, such matrices are not zero-one matrices when there are multiple edges in the same direction connecting two vertices. Q) When to use Adjacency matrix or adjacency list? • a simple graph contains relatively few edges, that is, when it is sparse • a simple graph is dense, when the graph contains more than half of all possible edges.

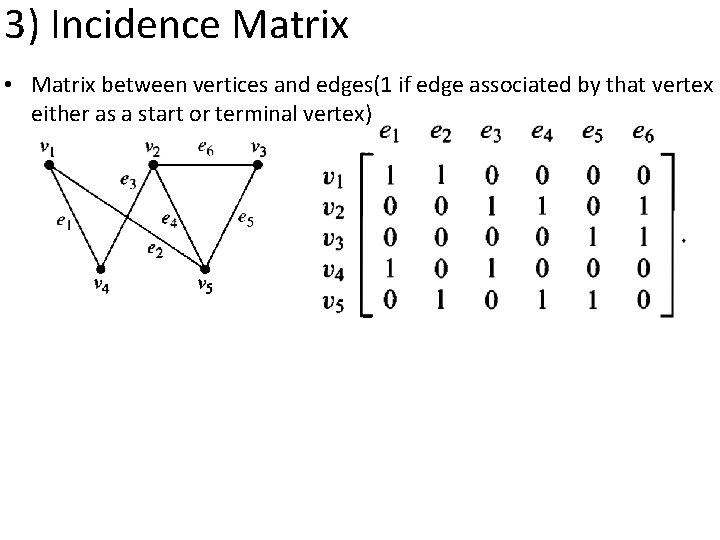
3) Incidence Matrix • Matrix between vertices and edges(1 if edge associated by that vertex either as a start or terminal vertex)

Isomorphism of Graph • whether it is possible to draw two graphs in the same way. • The simple graphs G 1 = (V 1, E 1) and G 2 = (V 2, E 2) are isomorphic if there is a one-to-one and onto function f (one-to-one correspondence) from V 1 to V 2 with the property that a and b are adjacent in G 1 if and only if f(a) and f(b) are adjacent in G 2, for all a and b in V 1. Such a function f is called an isomorphism.

• To show if two or more graphs are isomorphic we try to show three graph properties(graph invariants are true) a) Same number of vertices (for one to one corresp. b/w vertices) b) Same number of edges (establishes a one-to-one correspondence between edges. ) c) the degrees of the vertices must be same. d) f preserves the presence and absence of edges. One helpful way to do this is to use adjacency matrices. OR And A vertex v of degree d in G must correspond to a vertex f(v) of degree d in H, because a vertex w in G is adjacent to v if and only if f( v) and f(w) are adjacent in H.

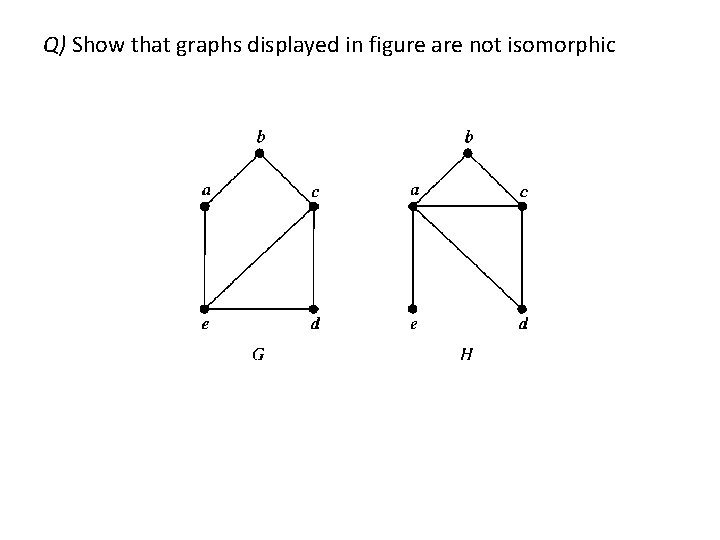
Q) Show that graphs displayed in figure are not isomorphic

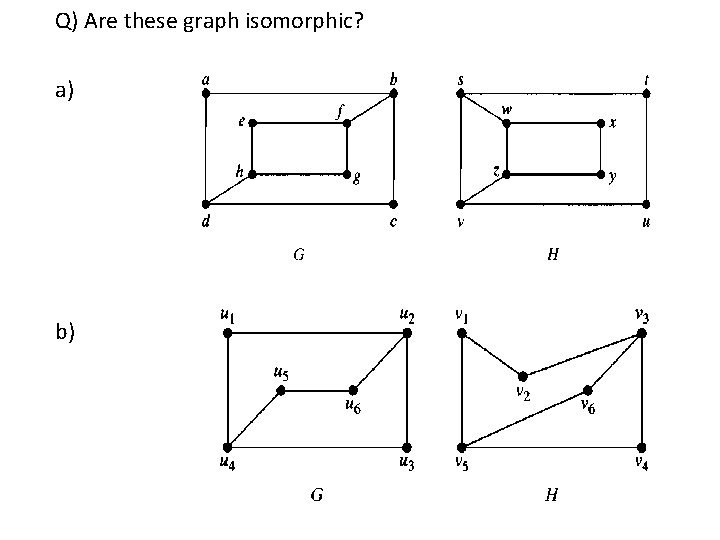
Q) Are these graph isomorphic? a) b)

Connectivity 1) Path