Graph A graph G is a set VG

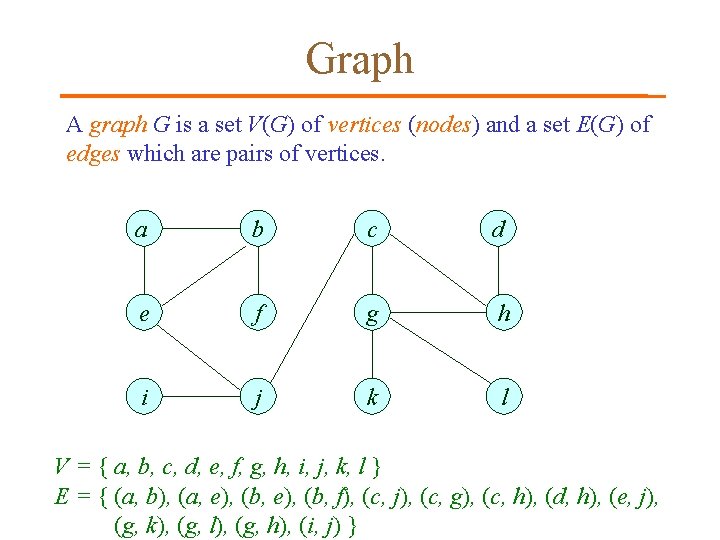
Graph A graph G is a set V(G) of vertices (nodes) and a set E(G) of edges which are pairs of vertices. a b c d e f g h i j k l V = { a, b, c, d, e, f, g, h, i, j, k, l } E = { (a, b), (a, e), (b, f), (c, j), (c, g), (c, h), (d, h), (e, j), (g, k), (g, l), (g, h), (i, j) }

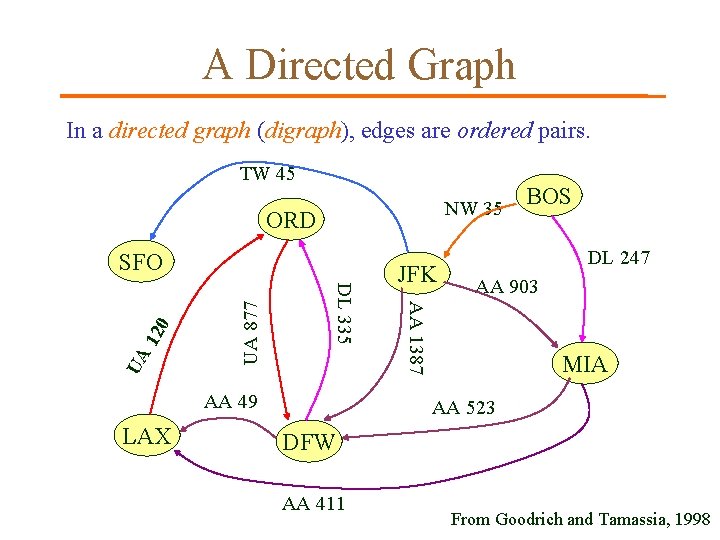
A Directed Graph In a directed graph (digraph), edges are ordered pairs. TW 45 NW 35 ORD UA 877 12 UA AA 49 LAX JFK DL 247 AA 903 AA 1387 DL 335 0 SFO BOS MIA AA 523 DFW AA 411 From Goodrich and Tamassia, 1998

Applications of Graphs describe relationships The Internet Streets / Highways (Roadmaps) Molecules Social Networks Geometric Surfaces (CAD) Circuits Parts in an Assembly …

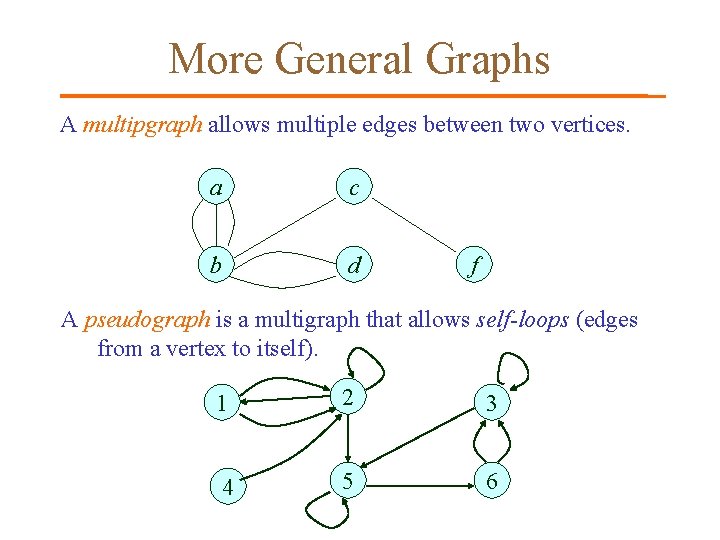
More General Graphs A multipgraph allows multiple edges between two vertices. a c b d f A pseudograph is a multigraph that allows self-loops (edges from a vertex to itself). 1 2 3 4 5 6

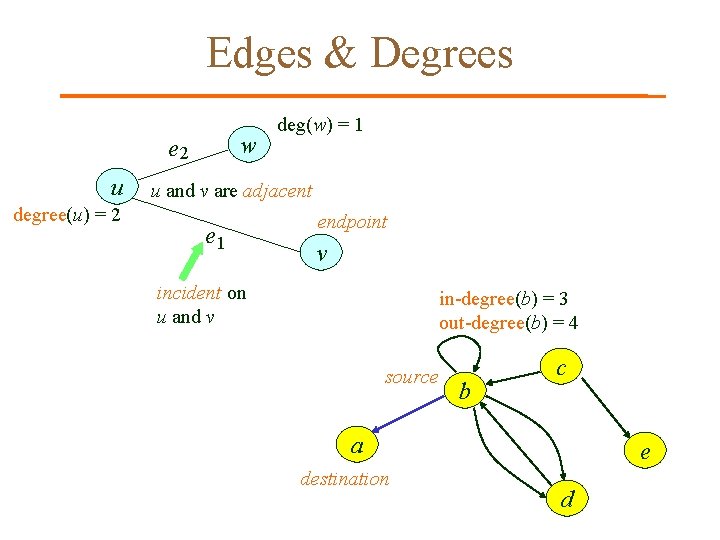
Edges & Degrees w e 2 u degree(u) = 2 deg(w) = 1 u and v are adjacent e 1 endpoint v incident on u and v in-degree(b) = 3 out-degree(b) = 4 source b c a destination e d

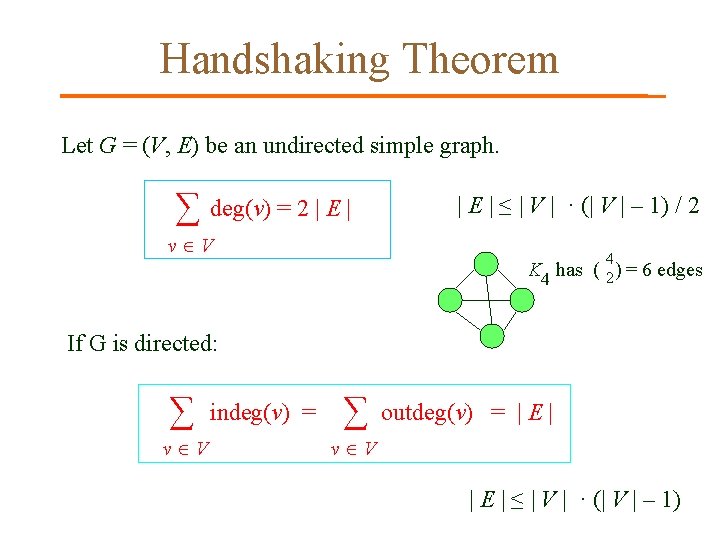
Handshaking Theorem Let G = (V, E) be an undirected simple graph. ∑ deg(v) = 2 | E | ≤ | V | · (| V | – 1) / 2 v V K 4 has ( 4 2) = 6 edges If G is directed: ∑ v V indeg(v) = ∑ outdeg(v) = | E | v V | E | ≤ | V | · (| V | – 1)

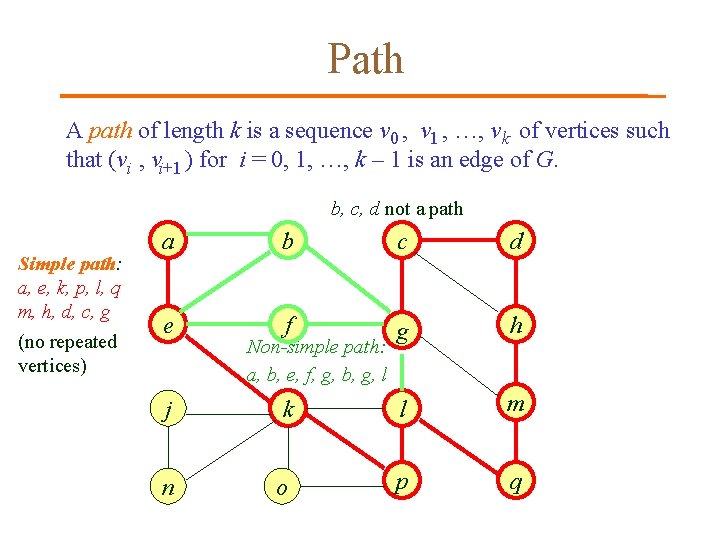
Path A path of length k is a sequence v 0 , v 1 , …, v k of vertices such that (vi , vi+1 ) for i = 0, 1, …, k – 1 is an edge of G. b, c, d not a path Simple path: a, e, k, p, l, q m, h, d, c, g (no repeated vertices) a b c d e f g h j k l m n o p q Non-simple path: a, b, e, f, g, b, g, l

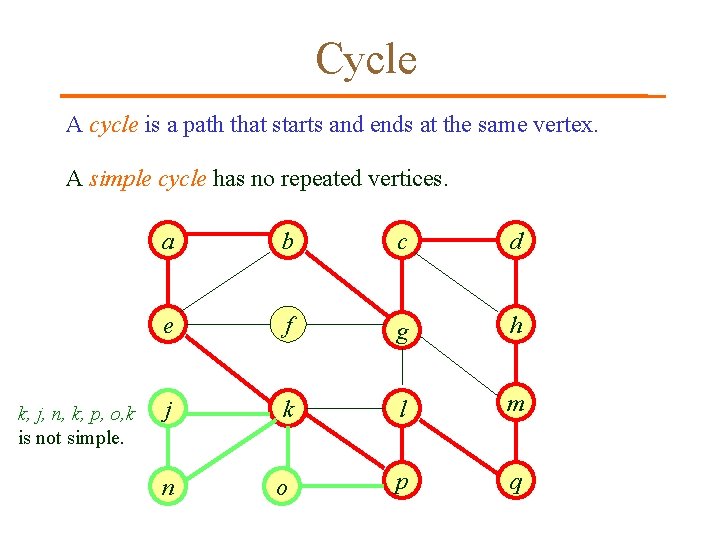
Cycle A cycle is a path that starts and ends at the same vertex. A simple cycle has no repeated vertices. k, j, n, k, p, o, k is not simple. a b c d e f g h j k l m n o p q

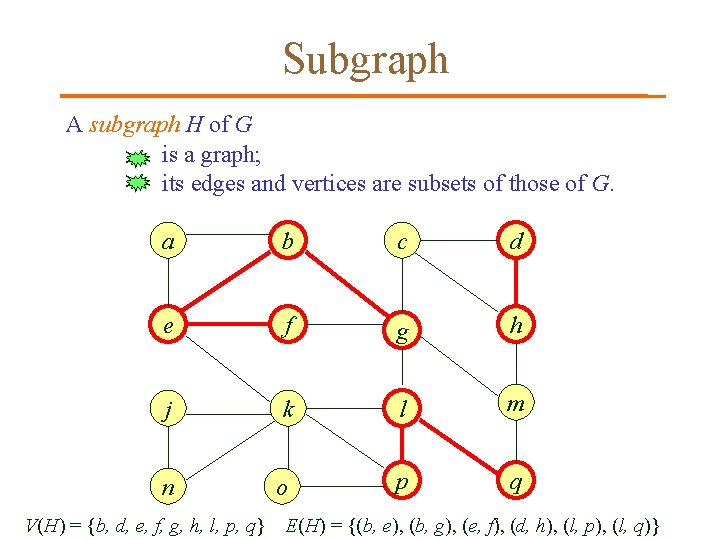
Subgraph A subgraph H of G is a graph; its edges and vertices are subsets of those of G. a b c d e f g h j k l m n o p q V(H) = {b, d, e, f, g, h, l, p, q} E(H) = {(b, e), (b, g), (e, f), (d, h), (l, p), (l, q)}

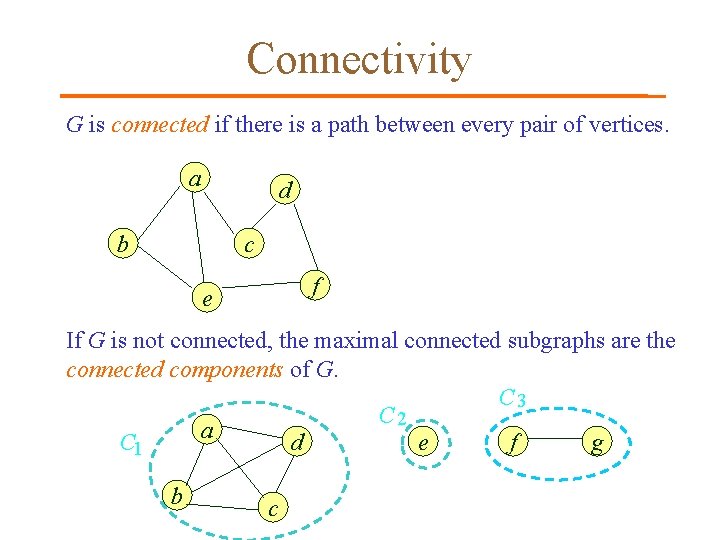
Connectivity G is connected if there is a path between every pair of vertices. a d b c f e If G is not connected, the maximal connected subgraphs are the connected components of G. C 3 C 2 a d e f g C 1 b c

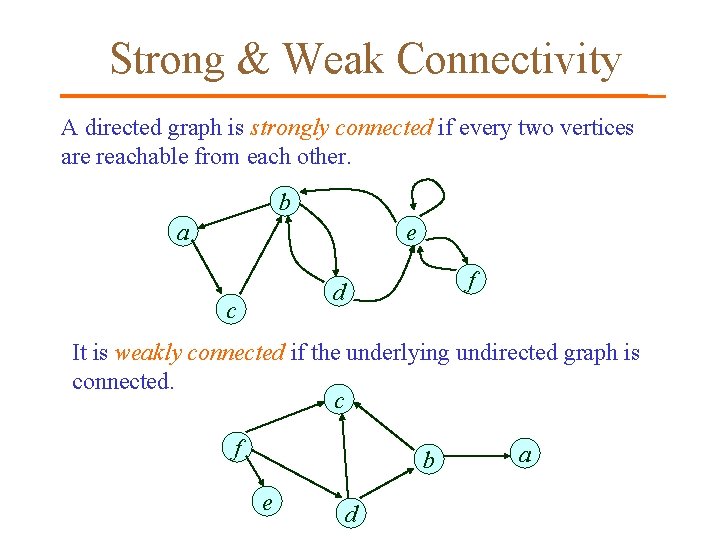
Strong & Weak Connectivity A directed graph is strongly connected if every two vertices are reachable from each other. b a e f d c It is weakly connected if the underlying undirected graph is connected. c f b e d a

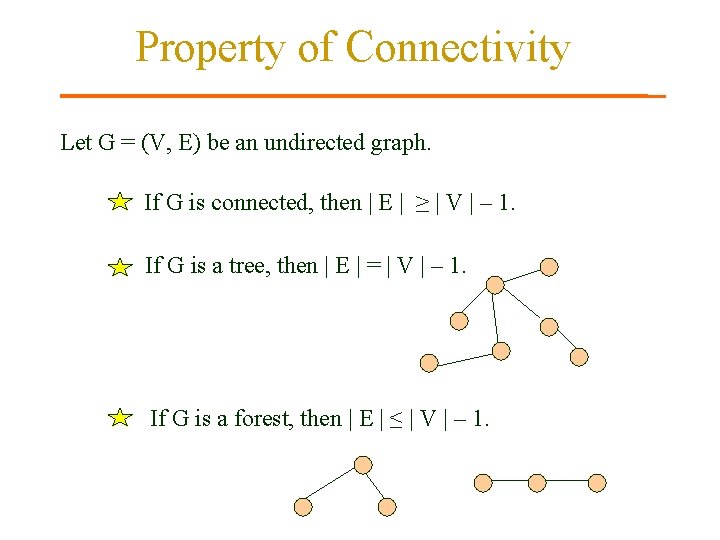
Property of Connectivity Let G = (V, E) be an undirected graph. If G is connected, then | E | ≥ | V | – 1. If G is a tree, then | E | = | V | – 1. If G is a forest, then | E | ≤ | V | – 1.

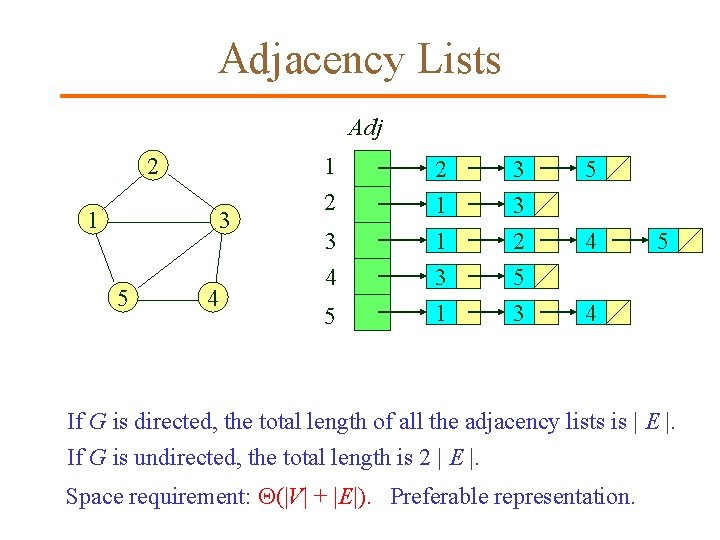
Adjacency Lists Adj 2 1 1 3 5 4 2 3 4 5 2 1 1 3 3 2 3 1 5 3 5 4 If G is directed, the total length of all the adjacency lists is | E |. If G is undirected, the total length is 2 | E |. Space requirement: (|V| + |E|). Preferable representation.

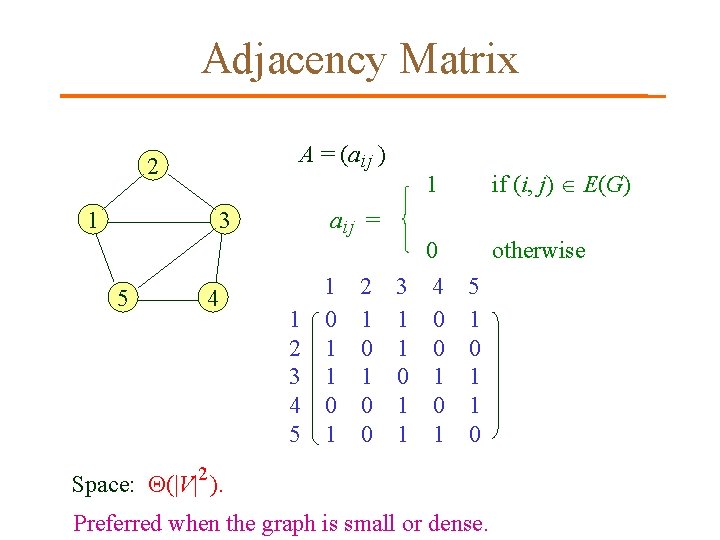
Adjacency Matrix A = (a ij ) 2 1 3 5 4 a ij = 1 2 3 4 5 1 2 3 0 1 1 1 0 0 0 1 1 if (i, j) E(G) 0 otherwise 4 5 0 1 0 0 1 1 0 Space: (|V|2 ). Preferred when the graph is small or dense.

Operation Time Operation Adjacency List Adjacency Matrix Scan incident edges (deg(v)) (|V|) Scan outgoing edges (outdeg(v)) (|V|) Scan incoming edges (indeg(v)) (|V|) Test adjacency of u and v Space (min(deg(u), deg(v)) (|V|+|E|) O(1) (|V| 2 ) Lecture notes modified over Dr. Fernandez-Baca’s