Grand Unified Algorithms How to retrieve radiatively consistent

Grand Unified Algorithms How to retrieve radiatively consistent profiles of clouds, precipitation and aerosol from radar, lidar and radiometers …and evaluating models Robin Hogan, University of Reading Thanks to Julien Delanoe, Nicola Pounder, Nicky Chalmers, Howard Barker

Spaceborne radar, lidar and radiometers Earth. Care The A-Train – NASA – 700 -km orbit – Cloud. Sat 94 -GHz radar (launch 2006) – Calipso 532/1064 -nm depol. lidar – MODIS multi-wavelength radiometer – CERES broad-band radiometer – AMSR-E microwave radiometer 2013 2019 2018 2017 2016 2015 Earth. CARE: launch 2012 2014 – ESA+JAXA – 400 -km orbit: more sensitive – 94 -GHz Doppler radar – 355 -nm HSRL/depol. lidar – Multispectral imager – Broad-band radiometer – Heart-warming name

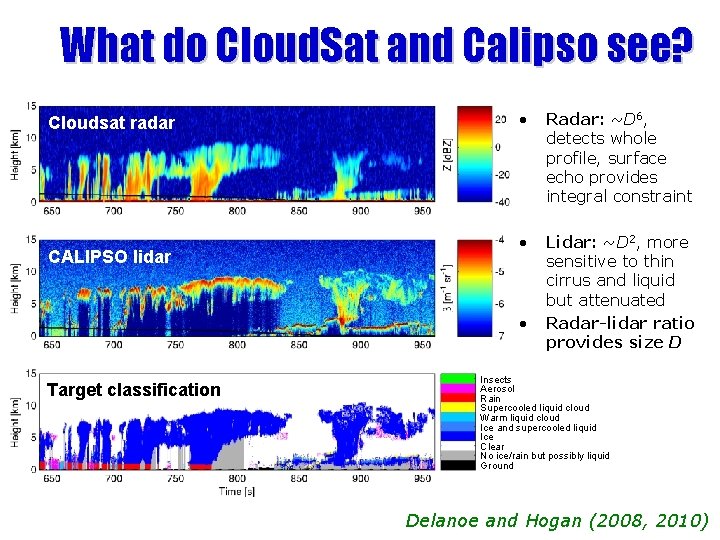
What do Cloud. Sat and Calipso see? Cloudsat radar CALIPSO lidar • Radar: ~D 6, detects whole profile, surface echo provides integral constraint • Lidar: ~D 2, more sensitive to thin cirrus and liquid but attenuated Radar-lidar ratio provides size D • Target classification Insects Aerosol Rain Supercooled liquid cloud Warm liquid cloud Ice and supercooled liquid Ice Clear No ice/rain but possibly liquid Ground Delanoe and Hogan (2008, 2010)

How do we evaluate models? • New approach – Forward-model observations and evaluate in obs. space – Ice. Sat lidar: Chepfer et al. (2007), Wilkinson et al. (2008) But these are the variables we – Cloud. Sat: Bodas et al. (2008) want to know! – Cloud. Sat & Calipso: IPCC/COSP Simple forward modeling can get right answer for wrong – Much easier! reasons, e. g. right Z with wrong – Avoids contamination by a. IWC and re priori information Can extract “hidden” info, e. g. – Avoids competition between re from radar-lidar synergy retrievals Can provide radiative verification of each retrieved profile But certainly more difficult! • Traditional approach – Compare retrieved cloud products to model variables – – –

Overview • Justification for and design of unified algorithm • Ice clouds – Evaluation against CERES – Evaluation of ECMWF and Met Office models • Liquid clouds – Fast multiple scattering model for exploitation of lidar signal – Extinction profile from multiple field-of-view lidar – Can we estimate liquid cloud base from the Calipso lidar? • First results from unified algorithm applied to A-Train – Simultaneous ice, liquid and rain retrievals • Outlook – 3 D radiatively consistent scene retrieval

“Grand Unified Algorithm” • Combine all measurements available (radar, lidar, radiometers) – Forms the observation vector y • Retrieve cloud, precipitation and aerosol properties simultaneously – Ensures integral measurements can be used when affected by more than one species (e. g. radiances affected by ice and liquid clouds) – Forms the state vector x • Variational approach – This is the proper way to do it! – Use forward model H(x) to predict observations from state vector – Report solution error covariance matrix & averaging kernel • Completely flexible – Applicable to ground-based, airborne and space-borne platforms • Behaviour should tend towards existing two-instrument synergy algos – Radar+lidar for ice clouds: Donovan et al. (2001), Tinel et al. (2005) – Cloud. Sat+MODIS for liquid clouds: Austin & Stephens (2001) – Calipso+MODIS for aerosol: Kaufman et al. (2003) – Cloud. Sat surface return for rainfall: L’Ecuyer & Stephens (2002)

The cost function • The essence of the method is to find the state vector x that minimizes a cost function: The forward model H(x) predicts the observations from the state vector x Each observation yi is weighted by the inverse of its error variance Some elements of x are constrained by a prior estimate This term can be used to penalize curvature in the retrieved profile

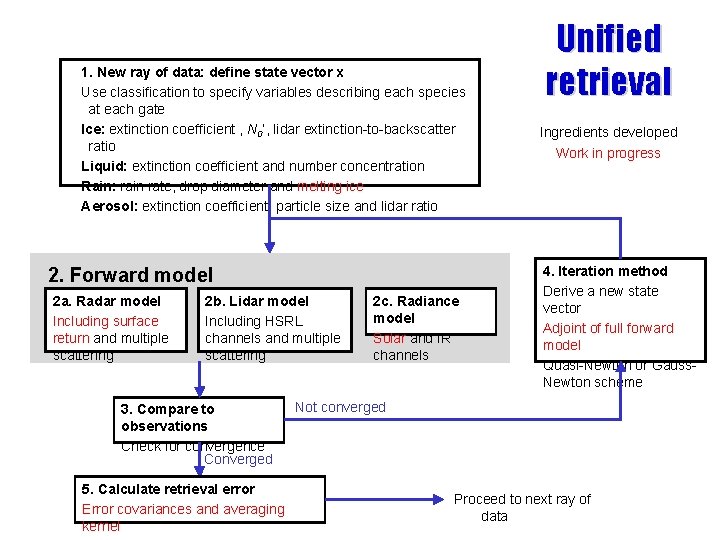
1. New ray of data: define state vector x Use classification to specify variables describing each species at each gate Ice: extinction coefficient , N 0’, lidar extinction-to-backscatter ratio Liquid: extinction coefficient and number concentration Rain: rain rate, drop diameter and melting ice Aerosol: extinction coefficient, particle size and lidar ratio 2. Forward model 2 a. Radar model Including surface return and multiple scattering 2 b. Lidar model Including HSRL channels and multiple scattering 3. Compare to observations Check for convergence Converged 5. Calculate retrieval error Error covariances and averaging kernel 2 c. Radiance model Solar and IR channels Unified retrieval Ingredients developed Work in progress 4. Iteration method Derive a new state vector Adjoint of full forward model Quasi-Newton or Gauss. Newton scheme Not converged Proceed to next ray of data

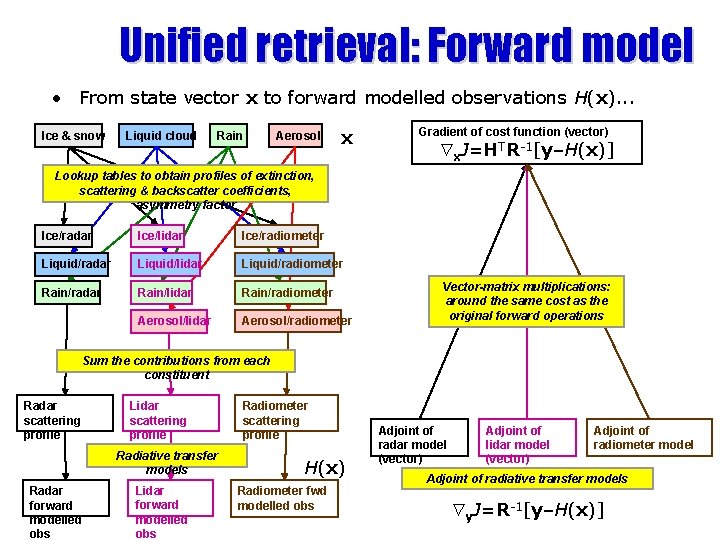
Unified retrieval: Forward model • From state vector x to forward modelled observations H(x). . . Ice & snow Liquid cloud Rain Aerosol x Gradient of cost function (vector) x. J=HTR-1[y–H(x)] Lookup tables to obtain profiles of extinction, scattering & backscatter coefficients, asymmetry factor Ice/radar Ice/lidar Ice/radiometer Liquid/radar Liquid/lidar Liquid/radiometer Rain/radar Rain/lidar Rain/radiometer Aerosol/lidar Aerosol/radiometer Vector-matrix multiplications: around the same cost as the original forward operations Sum the contributions from each constituent Radar scattering profile Lidar scattering profile Radiative transfer models Radar forward modelled obs Lidar forward modelled obs Radiometer scattering profile H(x) Radiometer fwd modelled obs Adjoint of radar model (vector) Adjoint of lidar model (vector) Adjoint of radiometer model Adjoint of radiative transfer models y. J=R-1[y–H(x)]

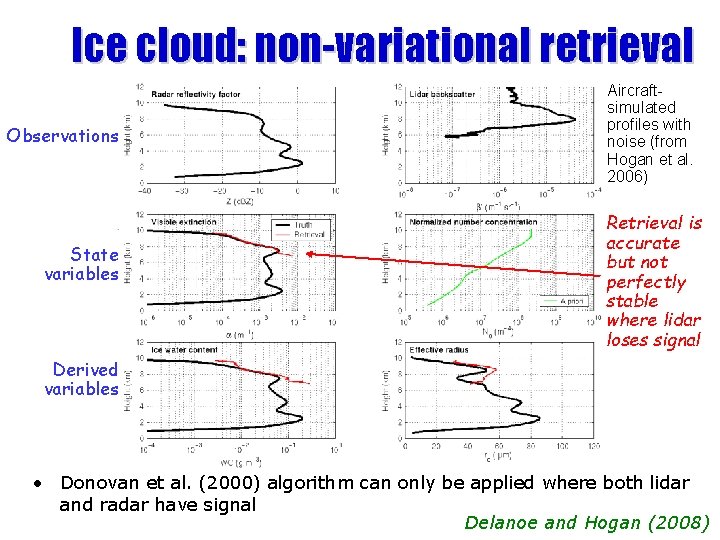
Ice cloud: non-variational retrieval Observations State variables Aircraftsimulated profiles with noise (from Hogan et al. 2006) Retrieval is accurate but not perfectly stable where lidar loses signal Derived variables • Donovan et al. (2000) algorithm can only be applied where both lidar and radar have signal Delanoe and Hogan (2008)

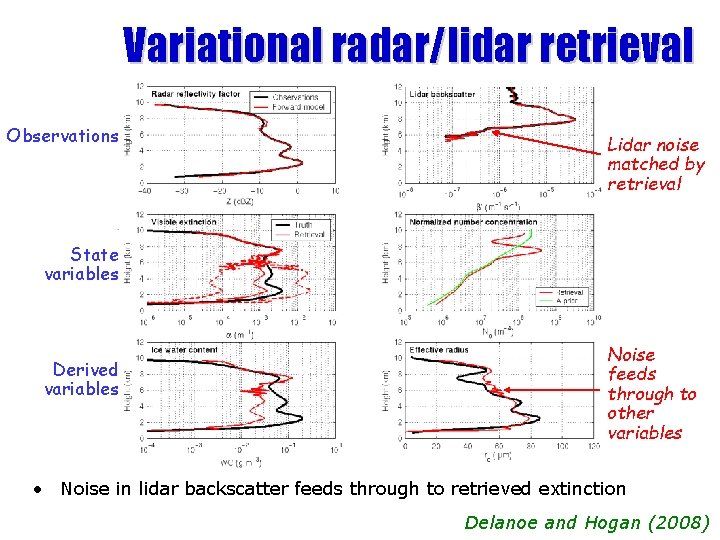
Variational radar/lidar retrieval Observations Lidar noise matched by retrieval State variables Derived variables Noise feeds through to other variables • Noise in lidar backscatter feeds through to retrieved extinction Delanoe and Hogan (2008)

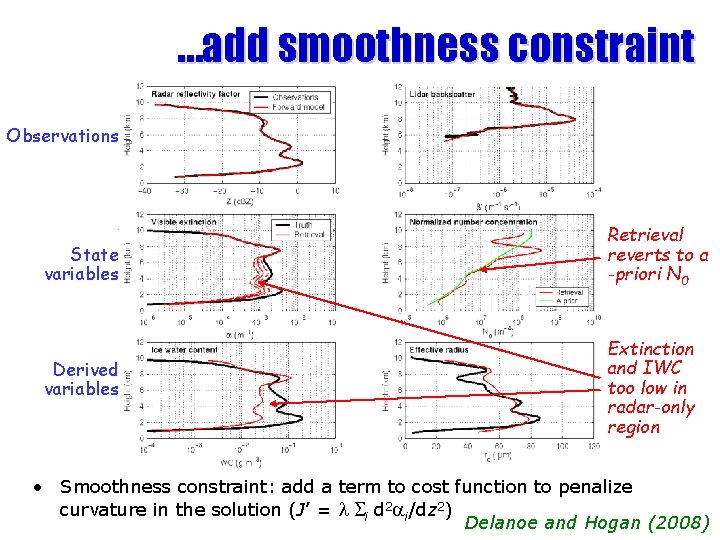
…add smoothness constraint Observations State variables Retrieval reverts to a -priori N 0 Derived variables Extinction and IWC too low in radar-only region • Smoothness constraint: add a term to cost function to penalize curvature in the solution (J’ = l Si d 2 ai/dz 2) Delanoe and Hogan (2008)

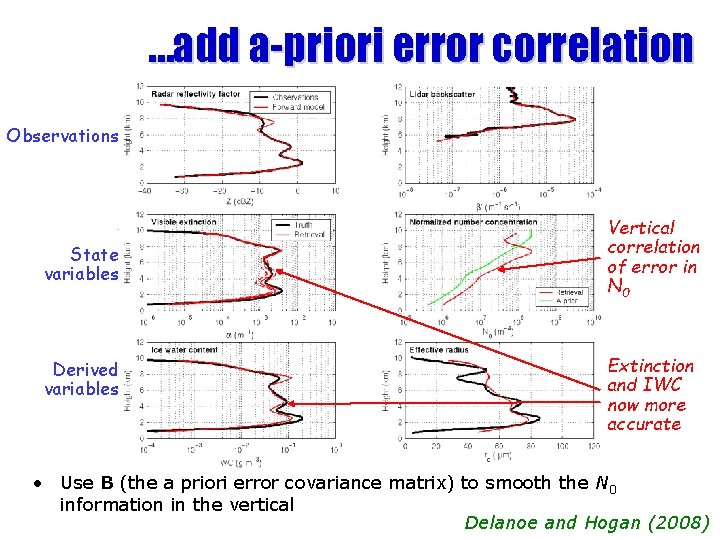
…add a-priori error correlation Observations State variables Derived variables Vertical correlation of error in N 0 Extinction and IWC now more accurate • Use B (the a priori error covariance matrix) to smooth the N 0 information in the vertical Delanoe and Hogan (2008)

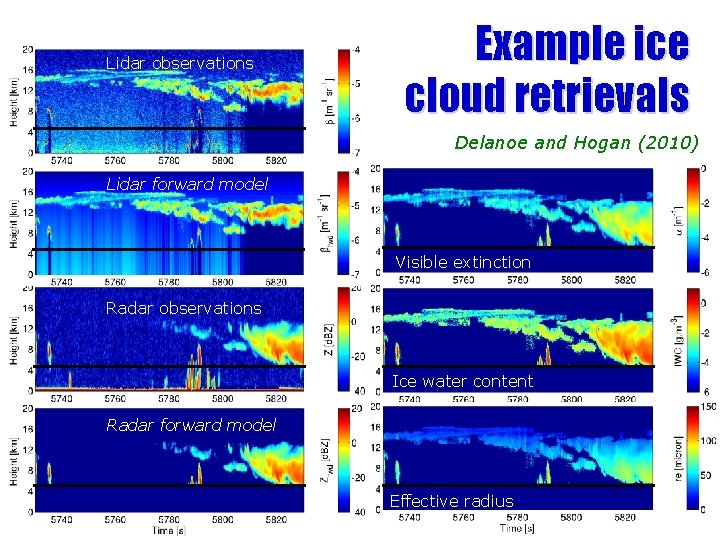
Lidar observations Example ice cloud retrievals Delanoe and Hogan (2010) Lidar forward model Visible extinction Radar observations Ice water content Radar forward model Effective radius

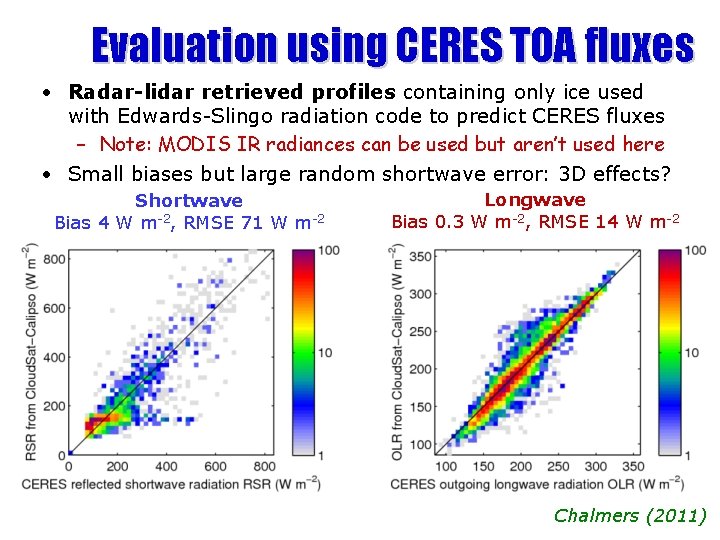
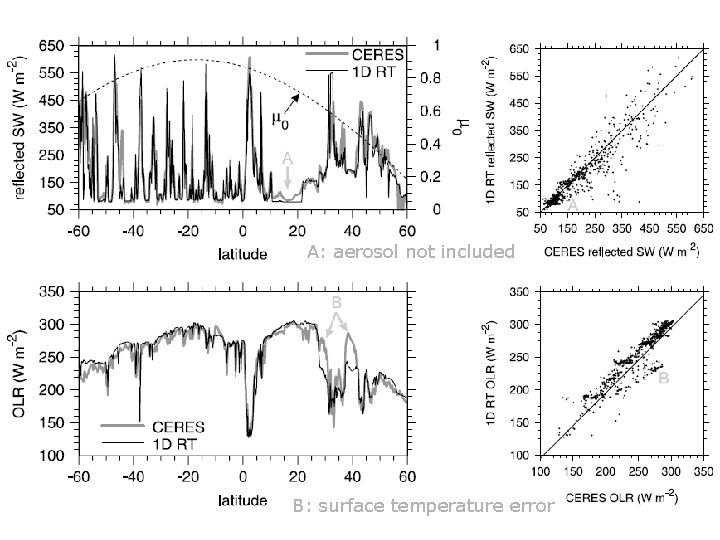
Evaluation using CERES TOA fluxes • Radar-lidar retrieved profiles containing only ice used with Edwards-Slingo radiation code to predict CERES fluxes – Note: MODIS IR radiances can be used but aren’t used here • Small biases but large random shortwave error: 3 D effects? Shortwave Bias 4 W m-2, RMSE 71 W m-2 Longwave Bias 0. 3 W m-2, RMSE 14 W m-2 Chalmers (2011)

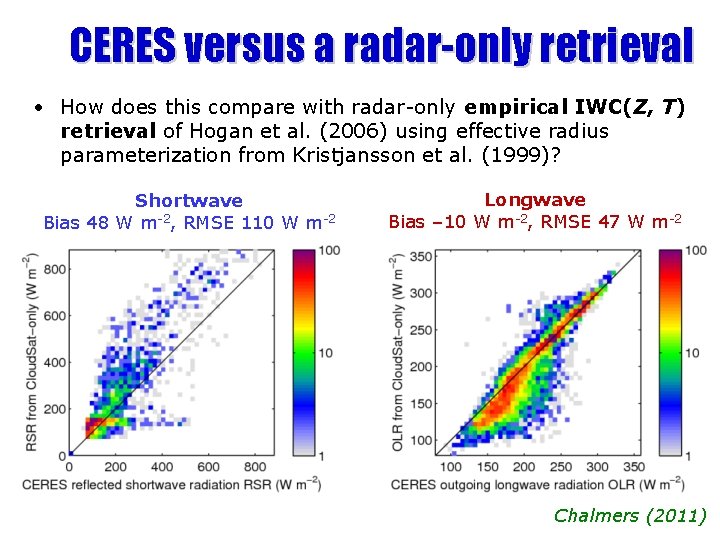
CERES versus a radar-only retrieval • How does this compare with radar-only empirical IWC(Z, T) retrieval of Hogan et al. (2006) using effective radius parameterization from Kristjansson et al. (1999)? Shortwave Bias 48 W m-2, RMSE 110 W m-2 Longwave Bias – 10 W m-2, RMSE 47 W m-2 Bias 10 W m-2 RMS 47 W m-2 Chalmers (2011)

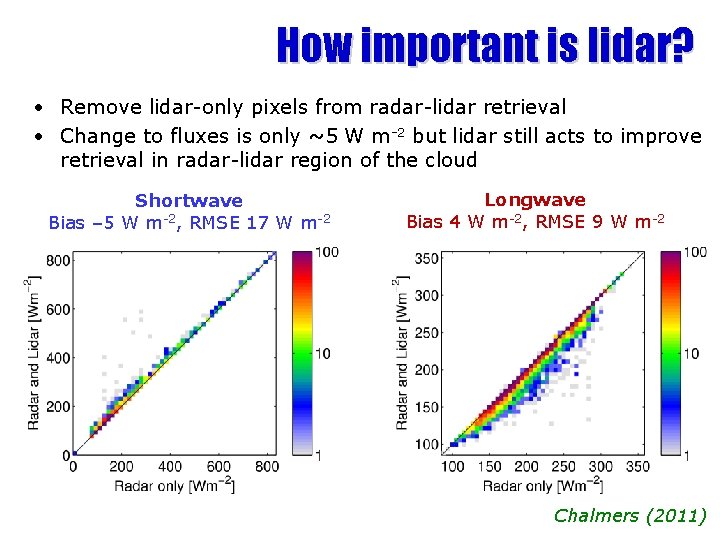
How important is lidar? • Remove lidar-only pixels from radar-lidar retrieval • Change to fluxes is only ~5 W m-2 but lidar still acts to improve retrieval in radar-lidar region of the cloud Shortwave Bias – 5 W m-2, RMSE 17 W m-2 Longwave Bias 4 W m-2, RMSE 9 W m-2 Chalmers (2011)

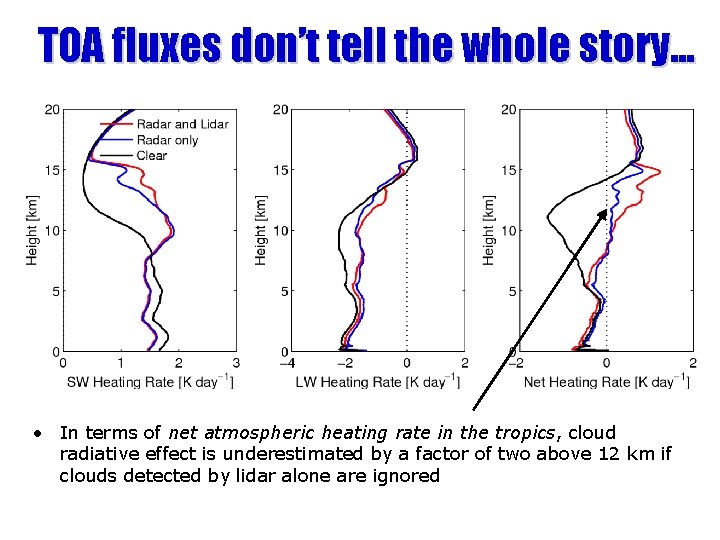
TOA fluxes don’t tell the whole story. . . • In terms of net atmospheric heating rate in the tropics, cloud radiative effect is underestimated by a factor of two above 12 km if clouds detected by lidar alone are ignored

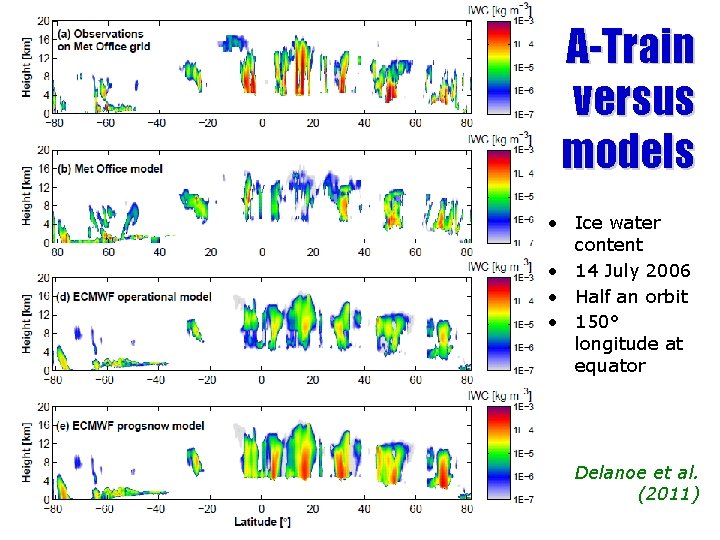
A-Train versus models • Ice water content • 14 July 2006 • Half an orbit • 150° longitude at equator Delanoe et al. (2011)

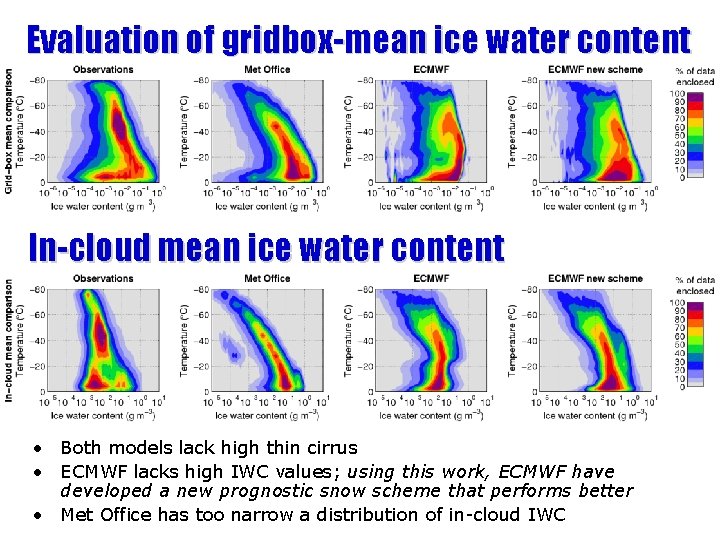
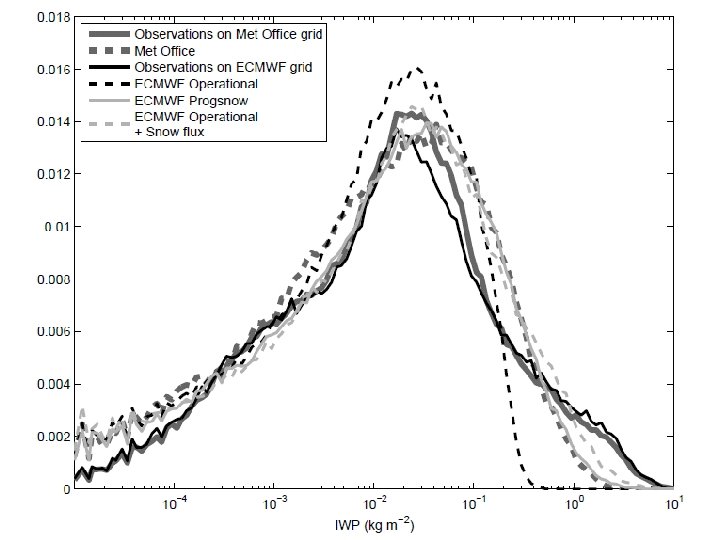
Evaluation of gridbox-mean ice water content In-cloud mean ice water content • Both models lack high thin cirrus • ECMWF lacks high IWC values; using this work, ECMWF have developed a new prognostic snow scheme that performs better • Met Office has too narrow a distribution of in-cloud IWC

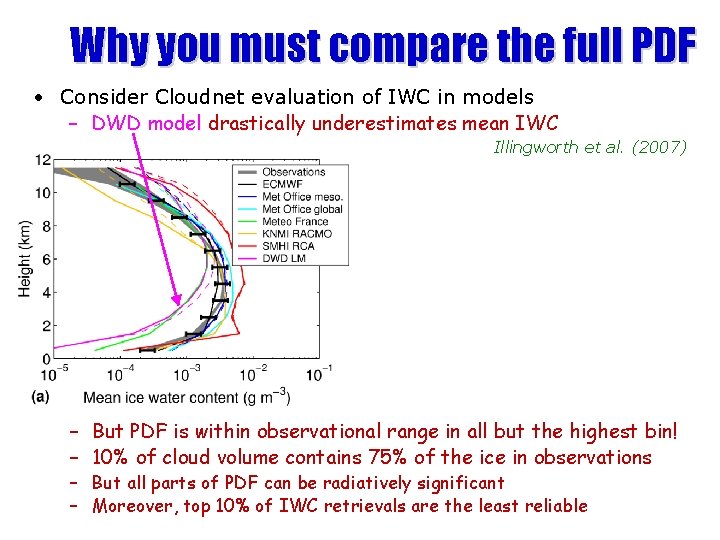
Why you must compare the full PDF • Consider Cloudnet evaluation of IWC in models – DWD model drastically underestimates mean IWC Illingworth et al. (2007) 3 -7 km – But PDF is within observational range in all but the highest bin! – 10% of cloud volume contains 75% of the ice in observations – But all parts of PDF can be radiatively significant – Moreover, top 10% of IWC retrievals are the least reliable

Liquid clouds • Stratocumulus clouds are tricky! – Lidar beam is rapidly attenuated – Radar return usually dominated by drizzle (Fox & Illingworth 1997) • Can we piece together their properties by forward modeling the following? – Multiply scattered lidar signal: information on optical depth and extinction profile – Surface radar return: path integrated attenuation proportional to liquid water path (Hawkness-Smith 2010) – Solar radiances: optical depth and droplet size / number concentration • We need: – Fast lidar forward model incorporating multiple scattering – Ability to use additional constraints, such as tendency for liquid water content profile to be adiabatic, particularly near cloud base CALIPSO Cloud. Sat

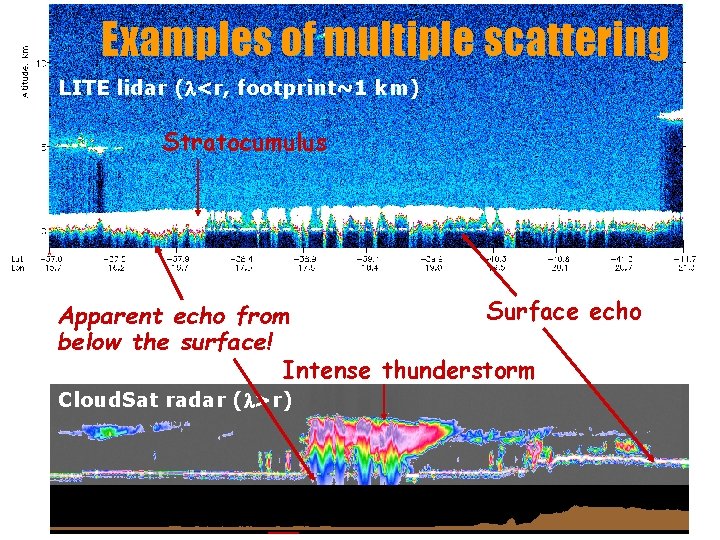
Examples of multiple scattering LITE lidar (l<r, footprint~1 km) Stratocumulus Surface echo Apparent echo from below the surface! Intense thunderstorm Cloud. Sat radar (l>r)

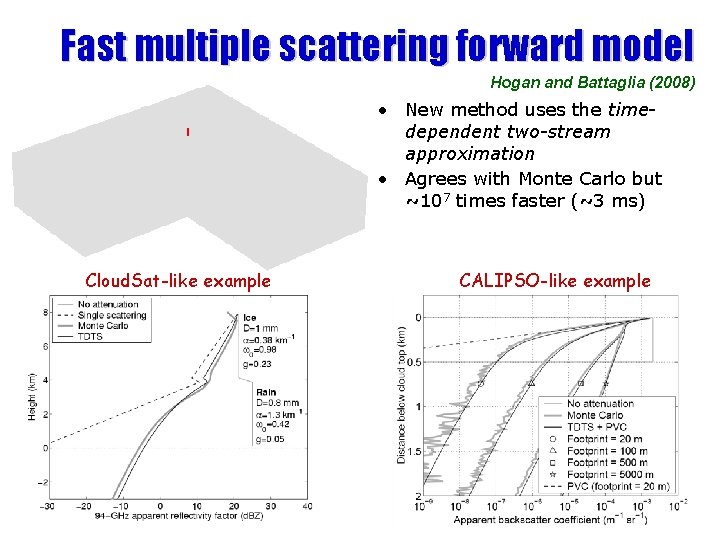
Time-dependent 2 -stream approx. • Describe diffuse flux in terms of outgoing stream I+ and incoming stream I–, and numerically integrate the following coupled PDEs: Source Time derivative Scattering from the quasi-direct beam into each of the streams Remove this and we have the timeindependent twostream approximation Spatial derivative Transport of radiation from upstream • Loss by absorption or scattering Some of lost radiation will enter the other stream Gain by scattering Radiation scattered from the other stream These can be discretized quite simply in time and space (no implicit methods or matrix inversion required) Hogan and Battaglia (2008)

Fast multiple scattering forward model Hogan and Battaglia (2008) • New method uses the timedependent two-stream approximation • Agrees with Monte Carlo but ~107 times faster (~3 ms) Cloud. Sat-like example CALIPSO-like example

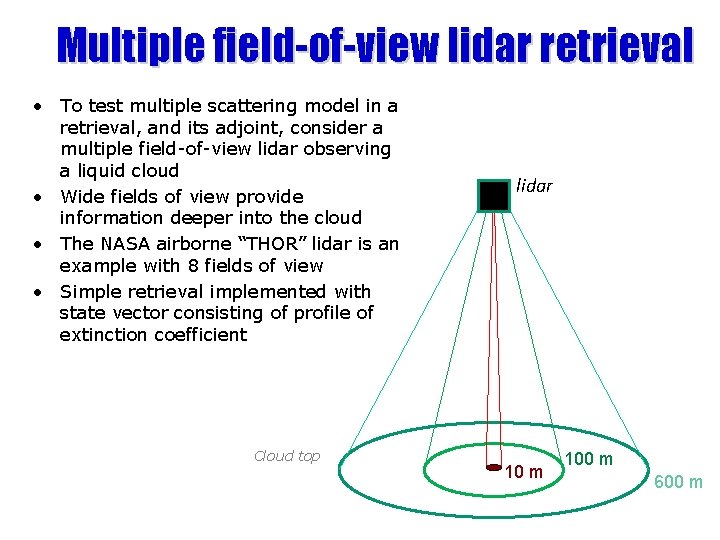
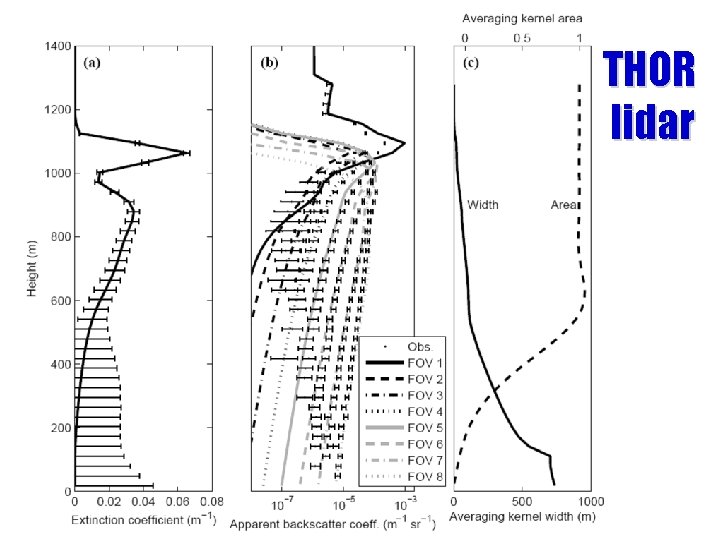
Multiple field-of-view lidar retrieval • To test multiple scattering model in a retrieval, and its adjoint, consider a multiple field-of-view lidar observing a liquid cloud • Wide fields of view provide information deeper into the cloud • The NASA airborne “THOR” lidar is an example with 8 fields of view • Simple retrieval implemented with state vector consisting of profile of extinction coefficient Cloud top lidar 10 m 100 m 600 m

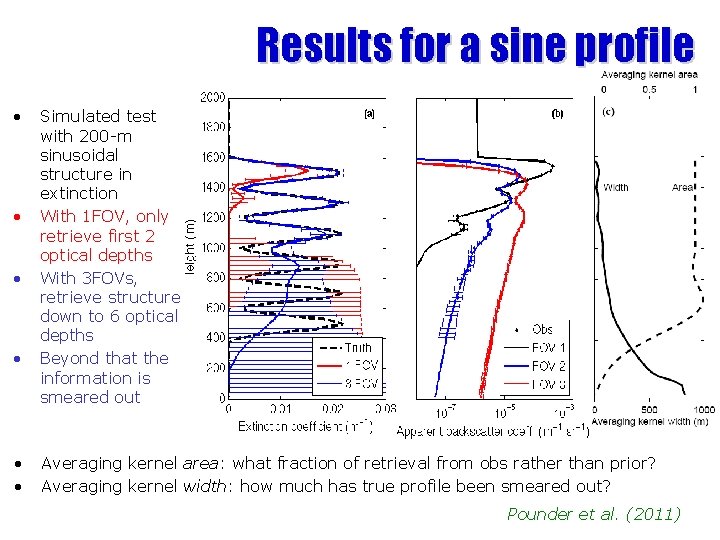
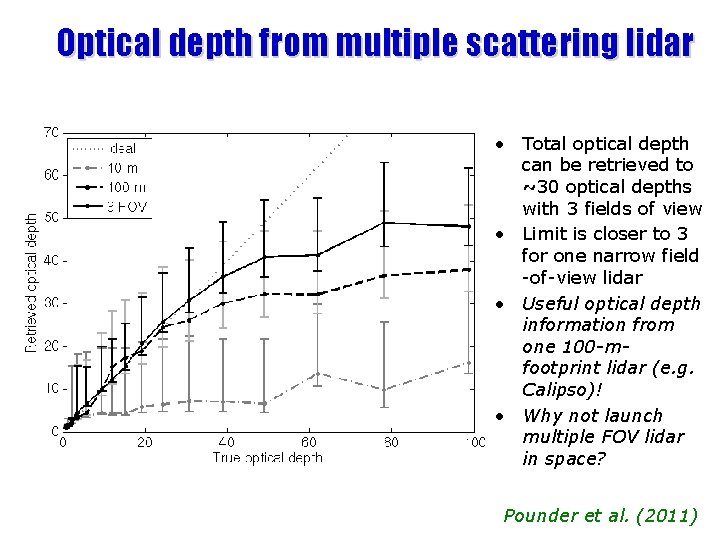
Results for a sine profile • • • Simulated test with 200 -m sinusoidal structure in extinction With 1 FOV, only retrieve first 2 optical depths With 3 FOVs, retrieve structure down to 6 optical depths Beyond that the information is smeared out Averaging kernel area: what fraction of retrieval from obs rather than prior? Averaging kernel width: how much has true profile been smeared out? Pounder et al. (2011)

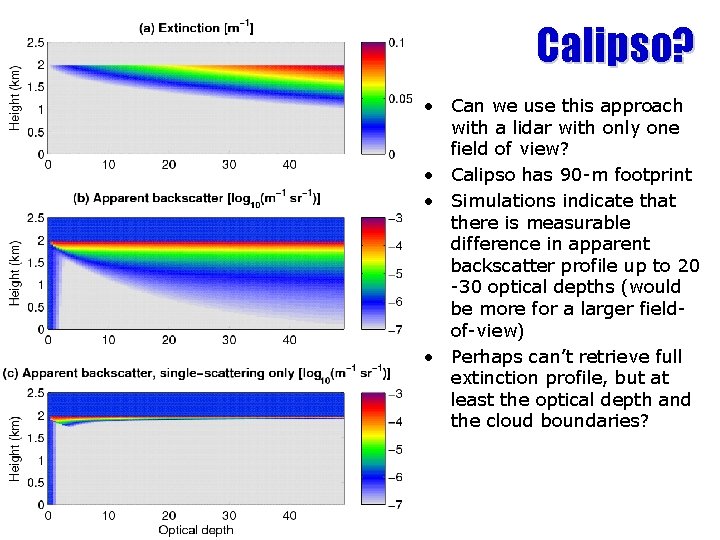
Calipso? • Can we use this approach with a lidar with only one field of view? • Calipso has 90 -m footprint • Simulations indicate that there is measurable difference in apparent backscatter profile up to 20 -30 optical depths (would be more for a larger fieldof-view) • Perhaps can’t retrieve full extinction profile, but at least the optical depth and the cloud boundaries?

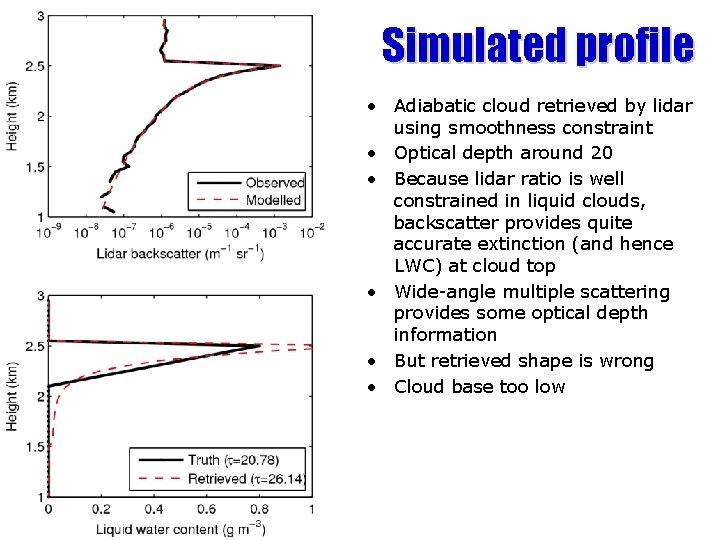
Simulated profile • Adiabatic cloud retrieved by lidar using smoothness constraint • Optical depth around 20 • Because lidar ratio is well constrained in liquid clouds, backscatter provides quite accurate extinction (and hence LWC) at cloud top • Wide-angle multiple scattering provides some optical depth information • But retrieved shape is wrong • Cloud base too low

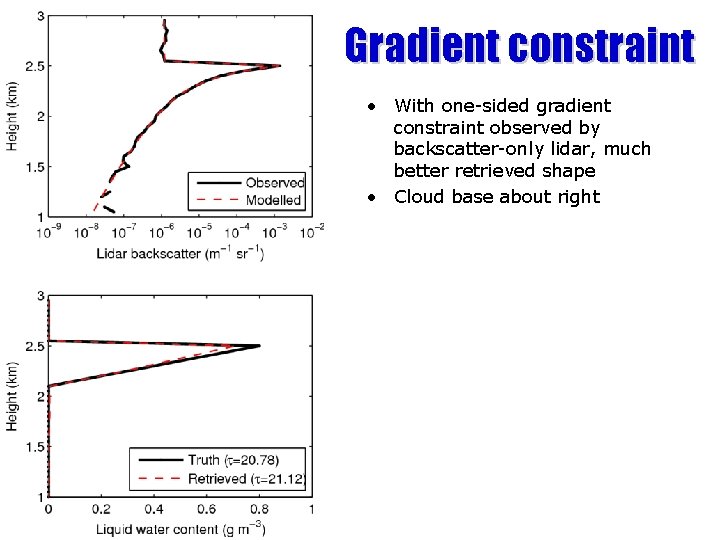
One-sided gradient constraint Slingo et al. (1982) • We have a good constraint on the gradient of LWC with height in stratocumulus: adiabatic profile, particularly near cloud base • Add an extra term to the cost function to penalize deviations from gradient c: • This term is only used when the LWC gradient is greater than c, so sub-adiabatic clouds can be retrieved • Test with simulated lidar-only retrieval of liquid water cloud using unified algorithm, and including simulated instrument noise

Gradient constraint • With one-sided gradient constraint observed by backscatter-only lidar, much better retrieved shape • Cloud base about right

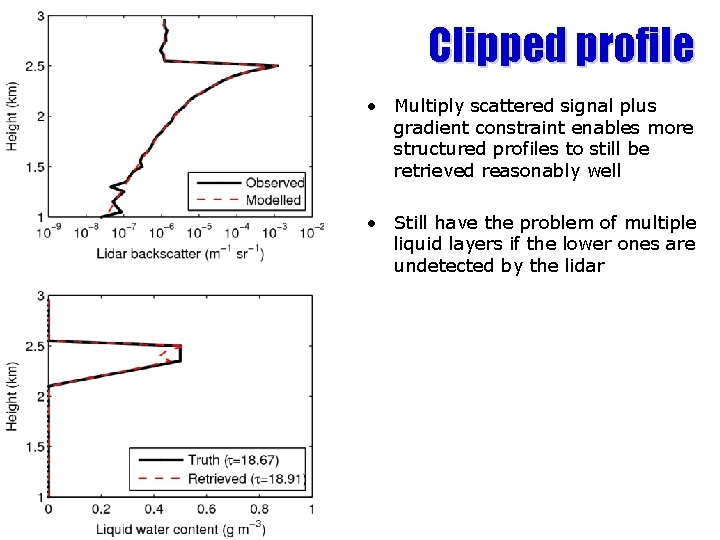
Clipped profile • Multiply scattered signal plus gradient constraint enables more structured profiles to still be retrieved reasonably well • Still have the problem of multiple liquid layers if the lower ones are undetected by the lidar

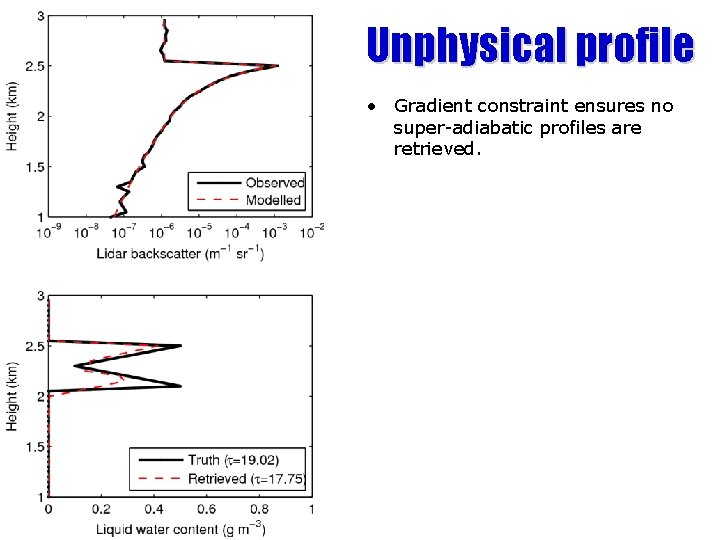
Unphysical profile • Gradient constraint ensures no super-adiabatic profiles are retrieved.

Optical depth from multiple scattering lidar • Total optical depth can be retrieved to ~30 optical depths with 3 fields of view • Limit is closer to 3 for one narrow field -of-view lidar • Useful optical depth information from one 100 -mfootprint lidar (e. g. Calipso)! • Why not launch multiple FOV lidar in space? Pounder et al. (2011)

Unified algorithm: progress • Bringing the aspects of this talk together… • Done: – Functioning algorithm framework exists – C++: object orientation allows code to be completely flexible: observations can be added and removed without needing to keep track of indices to matrices, so same code can be applied to different observing systems – Preliminary retrieval of ice, liquid, rain and aerosol – Adjoint of radar and lidar forward models with multiple scattering and HSRL/Raman support – Interface to L-BFGS quasi-Newton algorithm in GNU Scientific Library • In progress / future work: – Estimate and report error in solution and averaging kernel – Interface to radiance models – Test on a range of ground-based, airborne and spaceborne instruments – Will produce the standard Earth. CARE cloud & precip synergy products

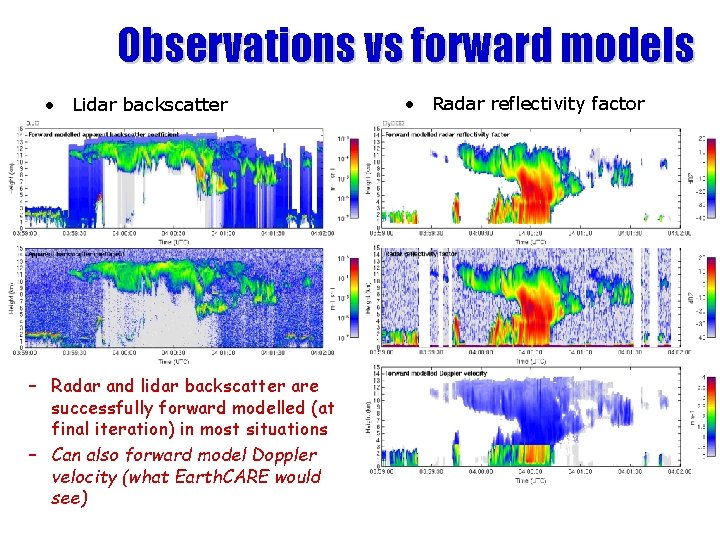
Observations vs forward models • Lidar backscatter – Radar and lidar backscatter are successfully forward modelled (at final iteration) in most situations – Can also forward model Doppler velocity (what Earth. CARE would see) • Radar reflectivity factor

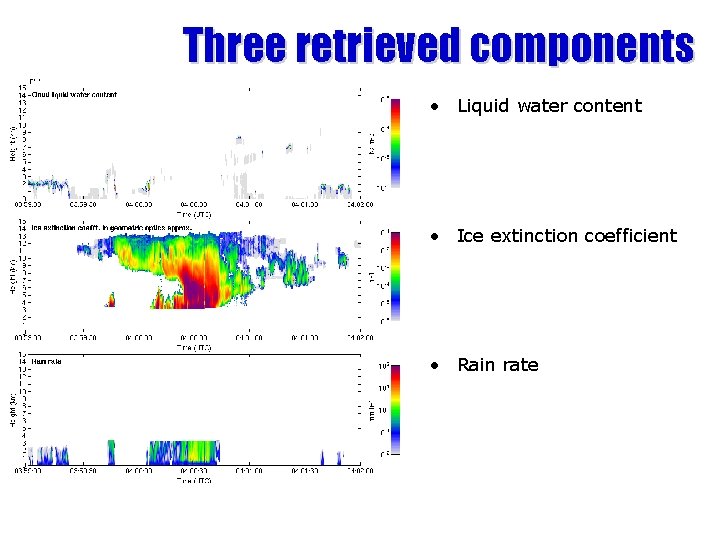
Three retrieved components • Liquid water content • Ice extinction coefficient • Rain rate

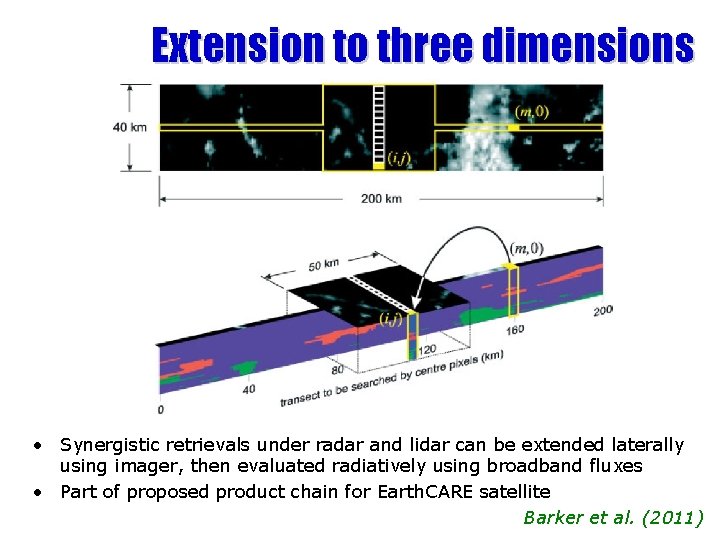
Extension to three dimensions • Synergistic retrievals under radar and lidar can be extended laterally using imager, then evaluated radiatively using broadband fluxes • Part of proposed product chain for Earth. CARE satellite Barker et al. (2011)

A: aerosol not included B: surface temperature error

Outlook • Evaluation of climate models in model space has distinct advantages over comparisons in observation space – Radiatively validated and consistent estimates of atmospheric state – Can say not only in what way model clouds are wrong but what the radiative consequence is – Forward-model errors affect both approaches • A “Grand Unified Algorithm” enables all measurements to be combined to provide the optimum estimate of the atmospheric state – Difficult and plenty remains to be done (e. g. precipitation – to be done with Pavlos Kolias) – Important to report errors (including those due to forward model errors) and averaging kernel information – Hope to have a fully flexible and freely available code that can be applied to many different platforms and accommodate new observations Three years of Cloud. Sat and Calipso ice retrievals: http: //www. icare. univ-lille 1. fr/projects/dardar/ (Google “dardar icare”)

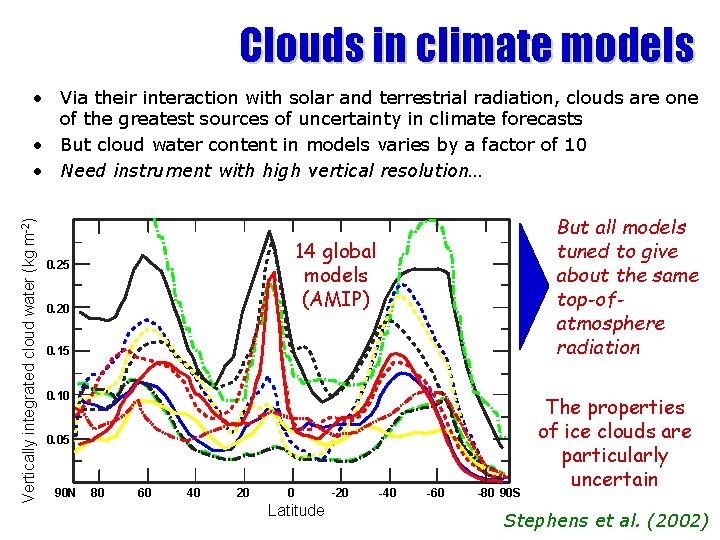
Clouds in climate models Vertically integrated cloud water (kg m-2) • Via their interaction with solar and terrestrial radiation, clouds are one of the greatest sources of uncertainty in climate forecasts • But cloud water content in models varies by a factor of 10 • Need instrument with high vertical resolution… But all models tuned to give about the same top-ofatmosphere radiation 14 global models (AMIP) 0. 25 0. 20 0. 15 0. 10 0. 05 90 N 80 60 40 20 0 Latitude -20 -40 -60 -80 90 S The properties of ice clouds are particularly uncertain Stephens et al. (2002)

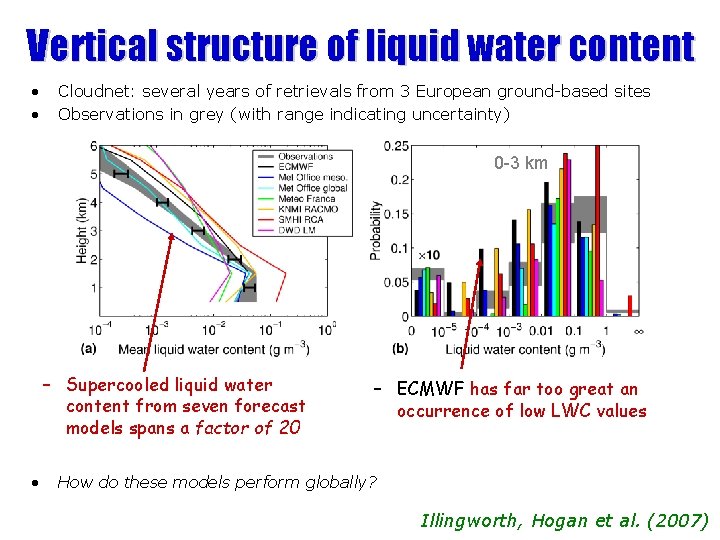
Vertical structure of liquid water content • • Cloudnet: several years of retrievals from 3 European ground-based sites Observations in grey (with range indicating uncertainty) 0 -3 km – Supercooled liquid water content from seven forecast models spans a factor of 20 • – ECMWF has far too great an occurrence of low LWC values How do these models perform globally? Illingworth, Hogan et al. (2007)

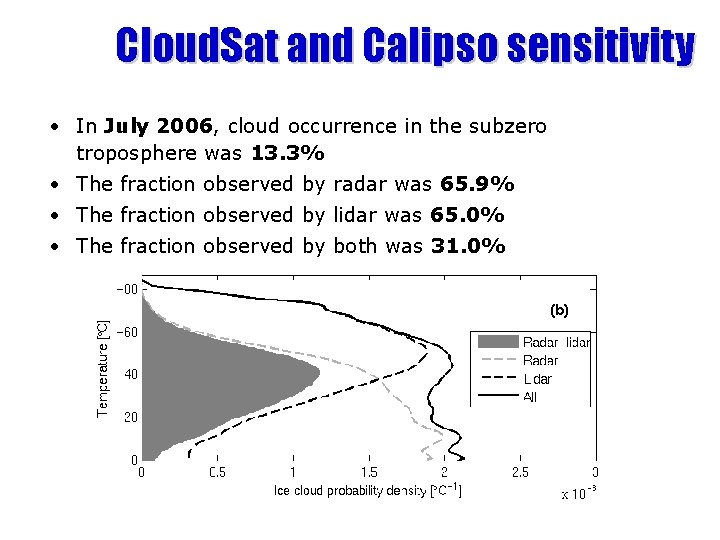
Cloud. Sat and Calipso sensitivity • In July 2006, cloud occurrence in the subzero troposphere was 13. 3% • The fraction observed by radar was 65. 9% • The fraction observed by lidar was 65. 0% • The fraction observed by both was 31. 0%

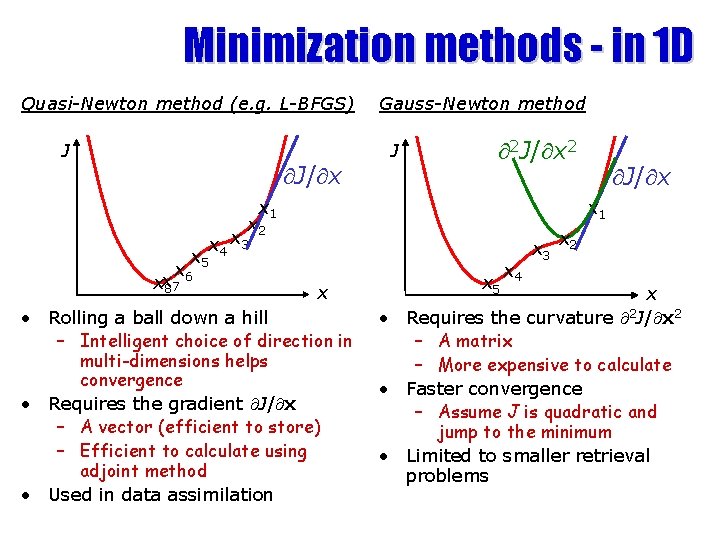
Minimization methods - in 1 D Quasi-Newton method (e. g. L-BFGS) J J/ x Gauss-Newton method J 2 J/ x 2 x 1 x 2 x 5 x xx 8 7 6 J/ x x 4 x 3 x • Rolling a ball down a hill – Intelligent choice of direction in multi-dimensions helps convergence • Requires the gradient J/ x – A vector (efficient to store) – Efficient to calculate using adjoint method • Used in data assimilation x 5 x 4 x 3 x 2 x • Requires the curvature 2 J/ x 2 – A matrix – More expensive to calculate • Faster convergence – Assume J is quadratic and jump to the minimum • Limited to smaller retrieval problems

Minimizing the cost function Gradient of cost function (a vector) and 2 nd derivative (the Hessian matrix): Gauss-Newton method Gradient Descent methods – – Fast adjoint method to calculate x. J means don’t need to calculate Jacobian – Disadvantage: more iterations needed since we don’t know curvature of J(x) – Quasi-Newton method to get the search direction (e. g. L-BFGS used by ECMWF): builds up an approximate inverse Hessian A for improved convergence – Scales well for large x – Poorer estimate of the error at the end – – – Rapid convergence (instant for linear problems) Get solution error covariance “for free” at the end Levenberg-Marquardt is a small modification to ensure convergence Need the Jacobian matrix H of every forward model: can be expensive for larger problems as forward model may need to be rerun with each element of the state vector perturbed

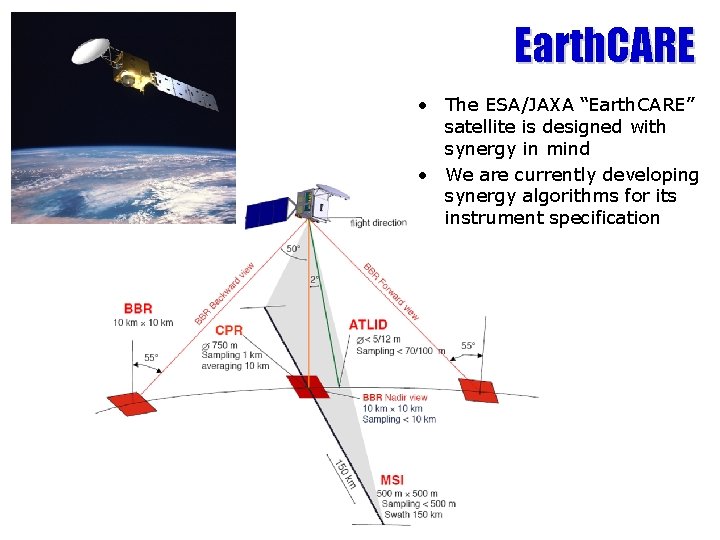
Earth. CARE • The ESA/JAXA “Earth. CARE” satellite is designed with synergy in mind • We are currently developing synergy algorithms for its instrument specification

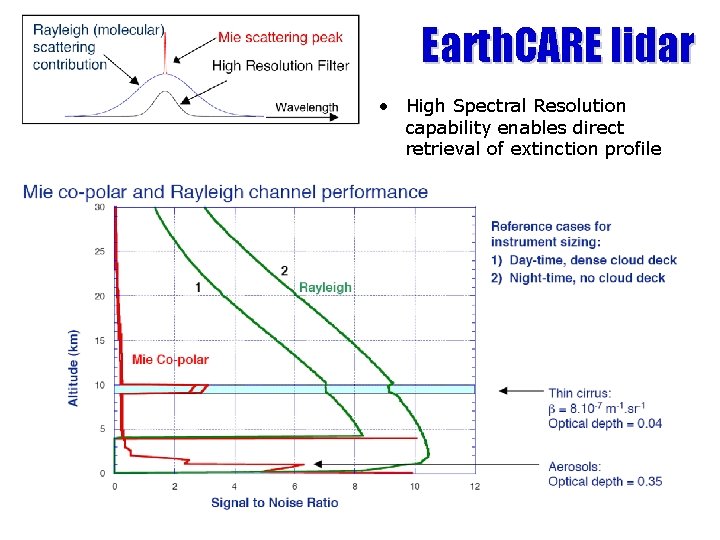
Earth. CARE lidar • High Spectral Resolution capability enables direct retrieval of extinction profile

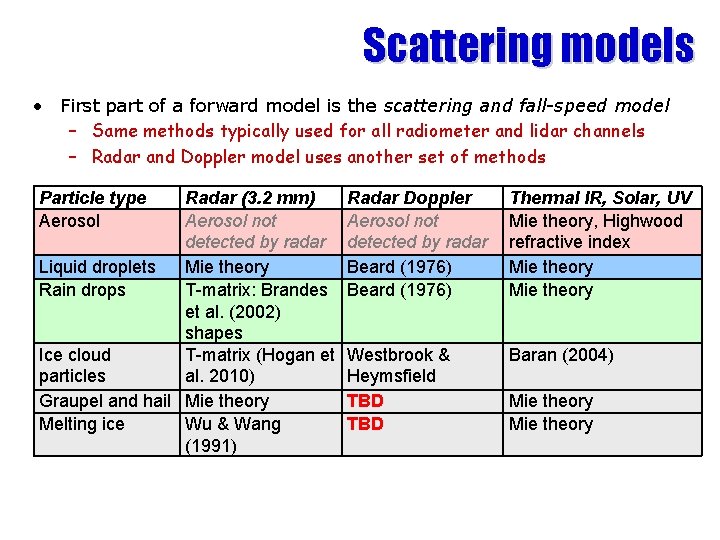
Scattering models • First part of a forward model is the scattering and fall-speed model – Same methods typically used for all radiometer and lidar channels – Radar and Doppler model uses another set of methods Particle type Aerosol Radar (3. 2 mm) Aerosol not detected by radar Liquid droplets Mie theory Rain drops T-matrix: Brandes et al. (2002) shapes Ice cloud T-matrix (Hogan et particles al. 2010) Graupel and hail Mie theory Melting ice Wu & Wang (1991) Radar Doppler Aerosol not detected by radar Beard (1976) Thermal IR, Solar, UV Mie theory, Highwood refractive index Mie theory Westbrook & Heymsfield TBD Baran (2004) Mie theory

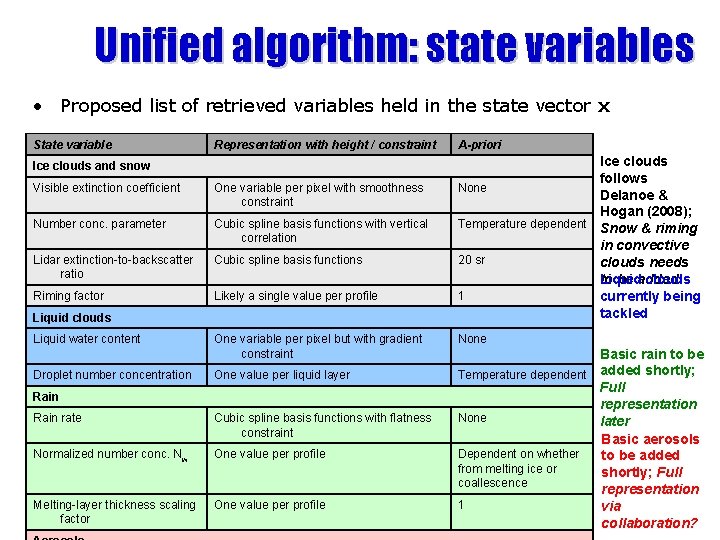
Unified algorithm: state variables • Proposed list of retrieved variables held in the state vector x State variable Representation with height / constraint Ice clouds and snow Visible extinction coefficient One variable per pixel with smoothness constraint Number conc. parameter Cubic spline basis functions with vertical correlation Lidar extinction-to-backscatter ratio Cubic spline basis functions Riming factor Likely a single value per profile Liquid clouds Liquid water content Droplet number concentration One variable per pixel but with gradient constraint One value per liquid layer Rain rate Cubic spline basis functions with flatness constraint Normalized number conc. Nw One value per profile Melting-layer thickness scaling factor One value per profile A-priori Ice clouds follows None Delanoe & Hogan (2008); Temperature dependent Snow & riming in convective 20 sr clouds needs to be added Liquid clouds 1 currently being tackled None Basic rain to be Temperature dependent added shortly; Full representation None later Basic aerosols Dependent on whether to be added from melting ice or shortly; Full coallescence representation 1 via collaboration?

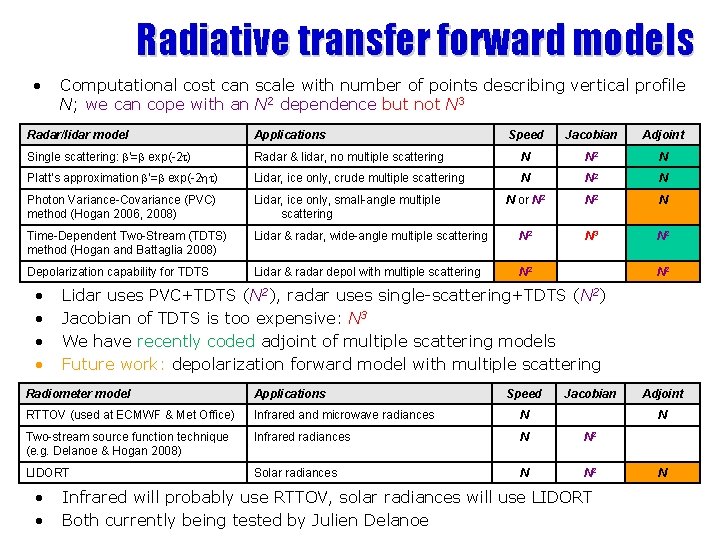
Radiative transfer forward models • Infrared radiances – Delanoe and Hogan (2008) model – Currently testing RTTOV (widely used, can do microwave, has adjoint) • Solar radiances – Currently testing LIDORT • Radar and lidar – Simplest model is single scattering with attenuation: b’=b exp(-2 d) – Problem from space is multiple scattering: contains extra information on cloud properties (particularly optical depth) but no-one has previously been able to rigorously make use of data subject to pulse stretching – Use combination of fast “Photon Variance-Covariance” method and “Time -Dependent Two-Stream” methods – Adjoints for these models recently coded – Forward model for lidar depolarization is in progress

Radiative transfer forward models • Computational cost can scale with number of points describing vertical profile N; we can cope with an N 2 dependence but not N 3 Radar/lidar model Applications Speed Jacobian Adjoint Single scattering: b’=b exp(-2 t) Radar & lidar, no multiple scattering N N 2 N Platt’s approximation b’=b exp(-2 ht) Lidar, ice only, crude multiple scattering N N 2 N Photon Variance-Covariance (PVC) method (Hogan 2006, 2008) Lidar, ice only, small-angle multiple scattering N or N 2 N Time-Dependent Two-Stream (TDTS) method (Hogan and Battaglia 2008) Lidar & radar, wide-angle multiple scattering N 2 N 3 N 2 Depolarization capability for TDTS Lidar & radar depol with multiple scattering N 2 • • N 2 Lidar uses PVC+TDTS (N 2), radar uses single-scattering+TDTS (N 2) Jacobian of TDTS is too expensive: N 3 We have recently coded adjoint of multiple scattering models Future work: depolarization forward model with multiple scattering Radiometer model Applications RTTOV (used at ECMWF & Met Office) Infrared and microwave radiances N Two-stream source function technique (e. g. Delanoe & Hogan 2008) Infrared radiances N N 2 LIDORT Solar radiances N N 2 • • Speed Jacobian Adjoint N Infrared will probably use RTTOV, solar radiances will use LIDORT Both currently being tested by Julien Delanoe N

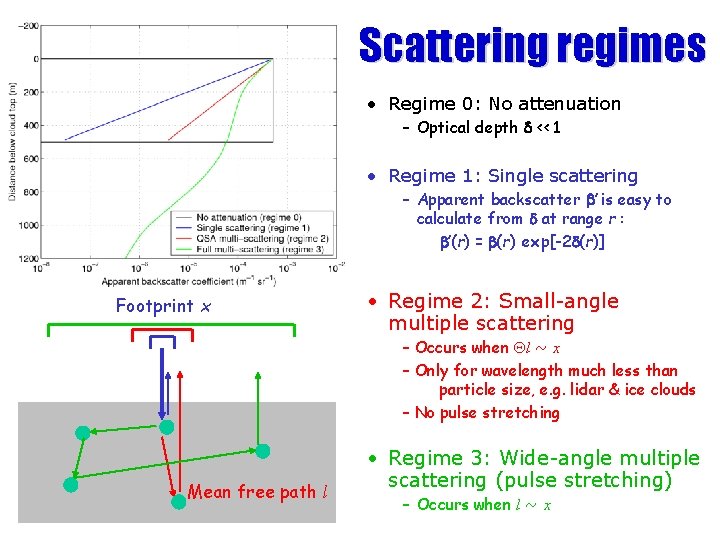
Scattering regimes • Regime 0: No attenuation – Optical depth d << 1 • Regime 1: Single scattering – Apparent backscatter b’ is easy to calculate from d at range r : b’(r) = b(r) exp[-2 d(r)] Footprint x • Regime 2: Small-angle multiple scattering – Occurs when Ql ~ x – Only for wavelength much less than particle size, e. g. lidar & ice clouds – No pulse stretching Mean free path l • Regime 3: Wide-angle multiple scattering (pulse stretching) – Occurs when l ~ x

THOR lidar

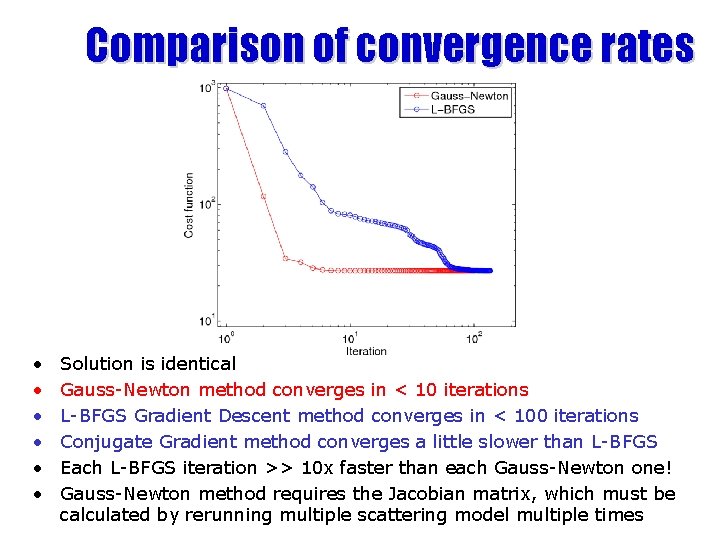
Comparison of convergence rates • • • Solution is identical Gauss-Newton method converges in < 10 iterations L-BFGS Gradient Descent method converges in < 100 iterations Conjugate Gradient method converges a little slower than L-BFGS Each L-BFGS iteration >> 10 x faster than each Gauss-Newton one! Gauss-Newton method requires the Jacobian matrix, which must be calculated by rerunning multiple scattering model multiple times

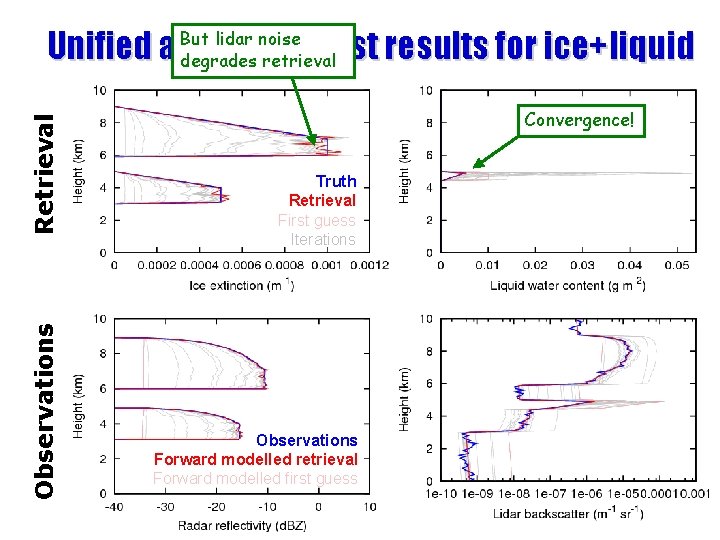
Observations Retrieval But lidar noise Unified algorithm: first results for ice+liquid degrades retrieval Convergence! Truth Retrieval First guess Iterations Observations Forward modelled retrieval Forward modelled first guess

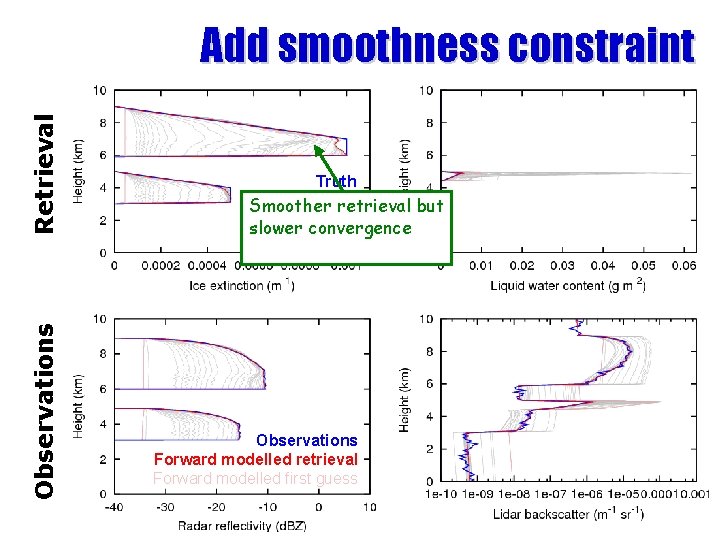
Observations Retrieval Add smoothness constraint Truth Retrieval Smoother retrieval but Firstconvergence guess slower Iterations Observations Forward modelled retrieval Forward modelled first guess

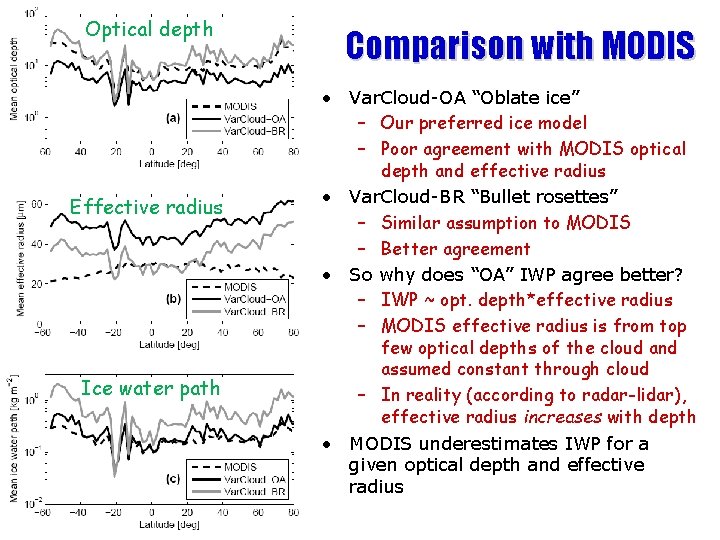
Optical depth Effective radius Ice water path Comparison with MODIS • Var. Cloud-OA “Oblate ice” – Our preferred ice model – Poor agreement with MODIS optical depth and effective radius • Var. Cloud-BR “Bullet rosettes” – Similar assumption to MODIS – Better agreement • So why does “OA” IWP agree better? – IWP ~ opt. depth*effective radius – MODIS effective radius is from top few optical depths of the cloud and assumed constant through cloud – In reality (according to radar-lidar), effective radius increases with depth • MODIS underestimates IWP for a given optical depth and effective radius

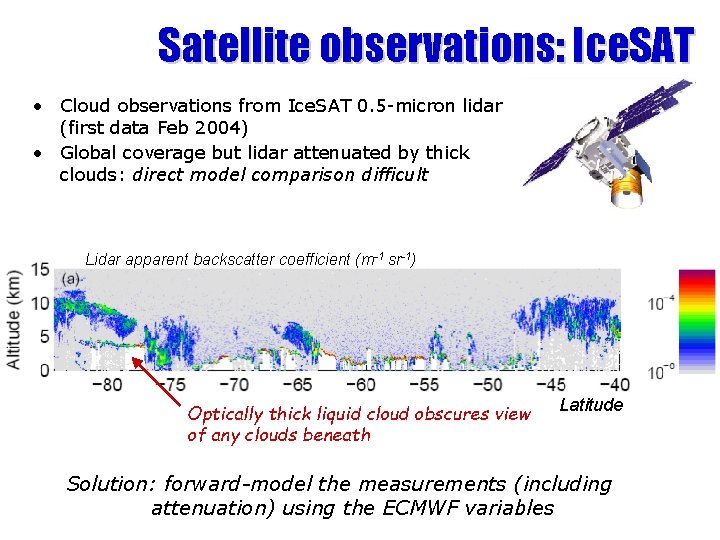
Satellite observations: Ice. SAT • Cloud observations from Ice. SAT 0. 5 -micron lidar (first data Feb 2004) • Global coverage but lidar attenuated by thick clouds: direct model comparison difficult Lidar apparent backscatter coefficient (m-1 sr-1) Optically thick liquid cloud obscures view of any clouds beneath Latitude Solution: forward-model the measurements (including attenuation) using the ECMWF variables

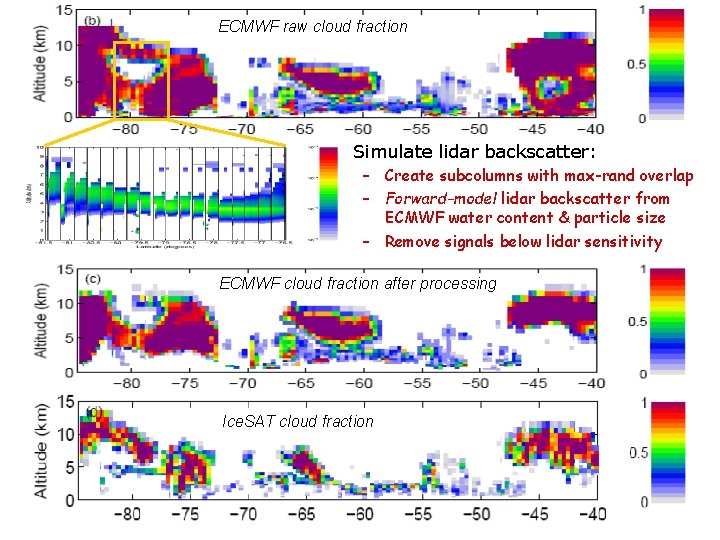
ECMWF raw cloud fraction Simulate lidar backscatter: – Create subcolumns with max-rand overlap – Forward-model lidar backscatter from ECMWF water content & particle size – Remove signals below lidar sensitivity ECMWF cloud fraction after processing Ice. SAT cloud fraction

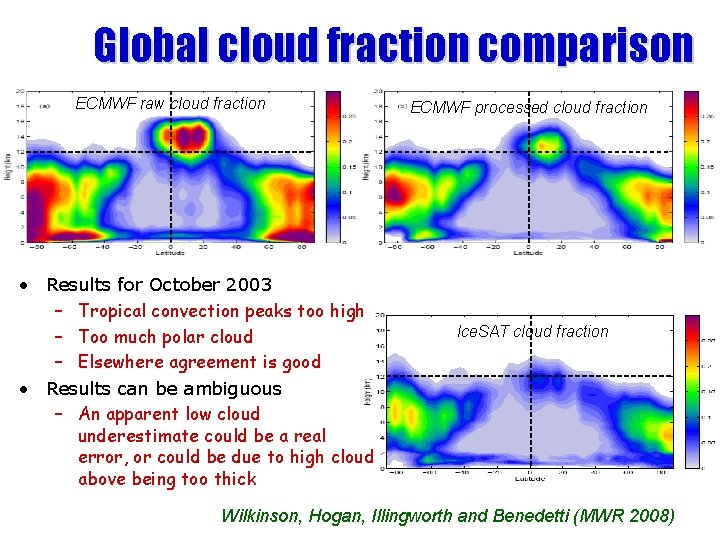
Global cloud fraction comparison ECMWF raw cloud fraction • Results for October 2003 – Tropical convection peaks too high – Too much polar cloud – Elsewhere agreement is good • Results can be ambiguous – An apparent low cloud underestimate could be a real error, or could be due to high cloud above being too thick ECMWF processed cloud fraction Ice. SAT cloud fraction Wilkinson, Hogan, Illingworth and Benedetti (MWR 2008)

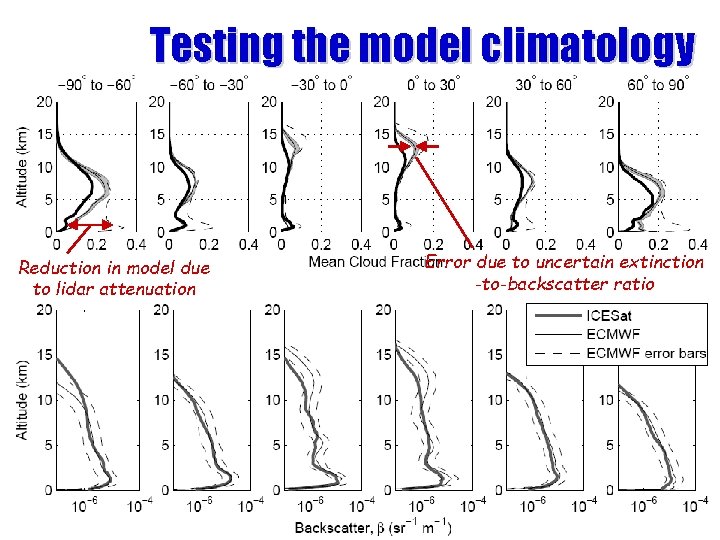
Testing the model climatology Reduction in model due to lidar attenuation Error due to uncertain extinction -to-backscatter ratio