grand gaugeHiggs unification 201138 based on ar Xiv

grand gauge-Higgs unification 山下 敏史 (名古屋 益川塾) 2011/3/8 @素粒子物理学の進展2011 based on : ar. Xiv: 1103. 1234 (appeared today) in collaboration with : K. Kojima (Kyushu) & K. Takenaga (Kumamoto Health Science)
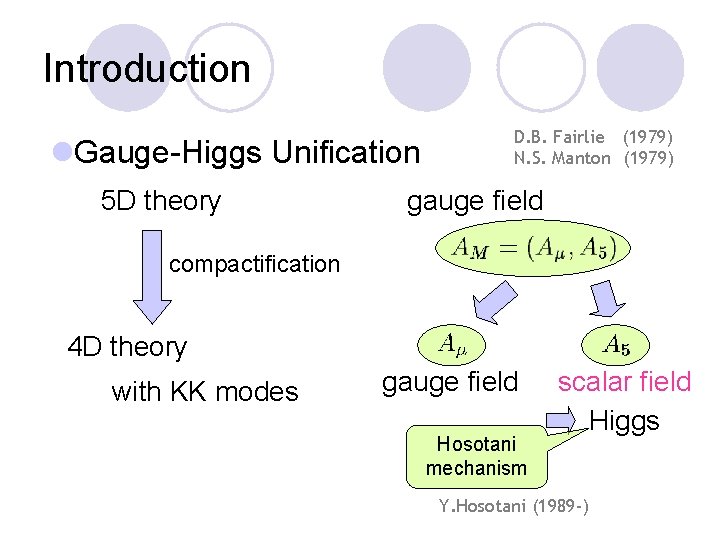
Introduction l. Gauge-Higgs Unification 5 D theory D. B. Fairlie (1979) N. S. Manton (1979) gauge field compactification 4 D theory with KK modes gauge field Hosotani mechanism scalar field Higgs Y. Hosotani (1989 -)
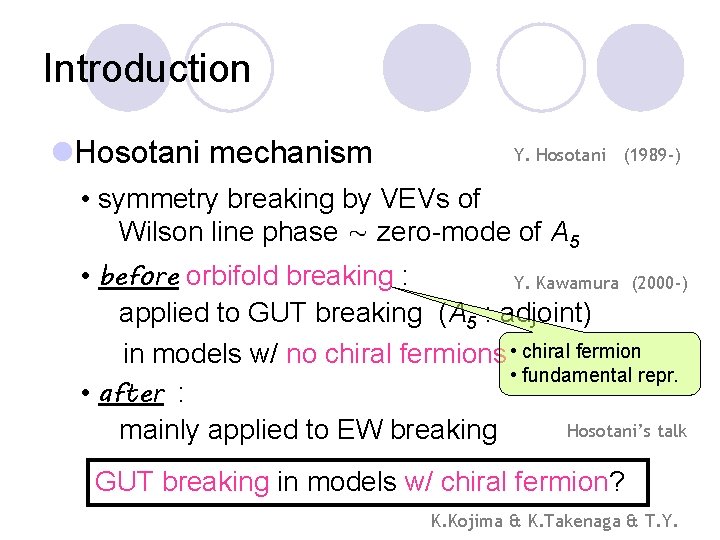
Introduction l. Hosotani mechanism Y. Hosotani (1989 -) • symmetry breaking by VEVs of Wilson line phase zero-mode of A 5 • before orbifold breaking : Y. Kawamura (2000 -) applied to GUT breaking (A 5 : adjoint) in models w/ no chiral fermions • chiral fermion • fundamental repr. • after : Hosotani’s talk mainly applied to EW breaking GUT breaking in models w/ chiral fermion? K. Kojima & K. Takenaga & T. Y.

Introduction ldifficulty K. Kojima & K. Takenaga & T. Y. • orbifold action projects out adjoint scalars • this difficulty is shared w/ heterotic string Kuwakino’s talk - well studied, classified w/ Kac-Moody level - ``diagonal embedding” method Why can’t we use this in our pheno. models?

Plan • • • Introduction massless adjoint scalar Fermions Applications Summary
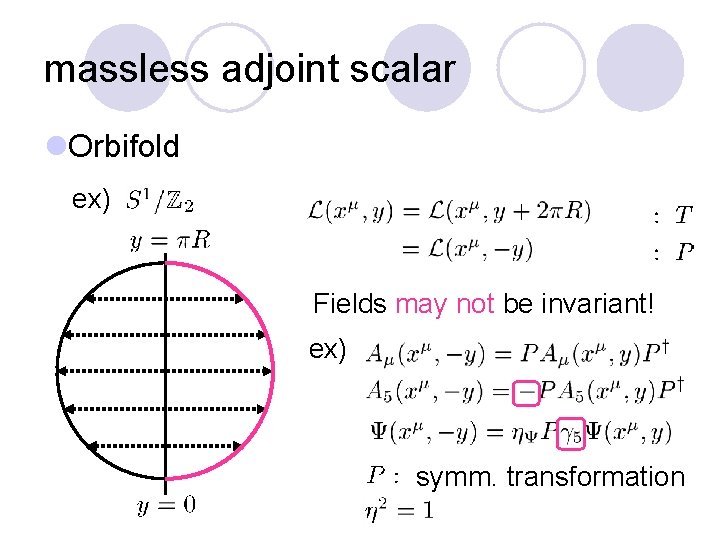
massless adjoint scalar l. Orbifold ex) Fields may not be invariant! ex) symm. transformation
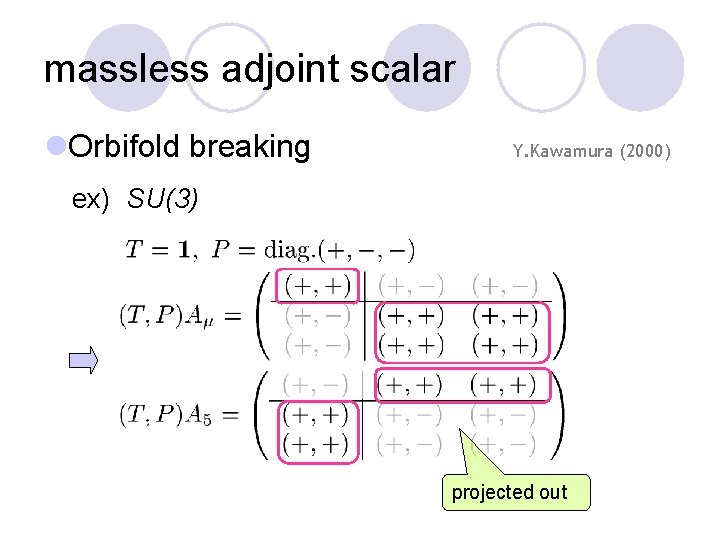
massless adjoint scalar l. Orbifold breaking Y. Kawamura (2000) ex) SU(3) SU(2)*U(1) projected out

massless adjoint scalar ldiagonal embedding diagonal part K. R. Dienes & J. March-Russel (1996) permutation eigenvalues: as orbifold action ex) adjoint scalar zero-modes:

Plan • • • Introduction massless adjoint scalar Fermions Applications Summary

Fermions K. Kojima & K. Takenaga & T. Y. lexchange symmetry Z 2 partner when R 1=R 2 : vector-like • when R 1=R 2 (=R) : ex) SU(5) w/ R=5 : chiral
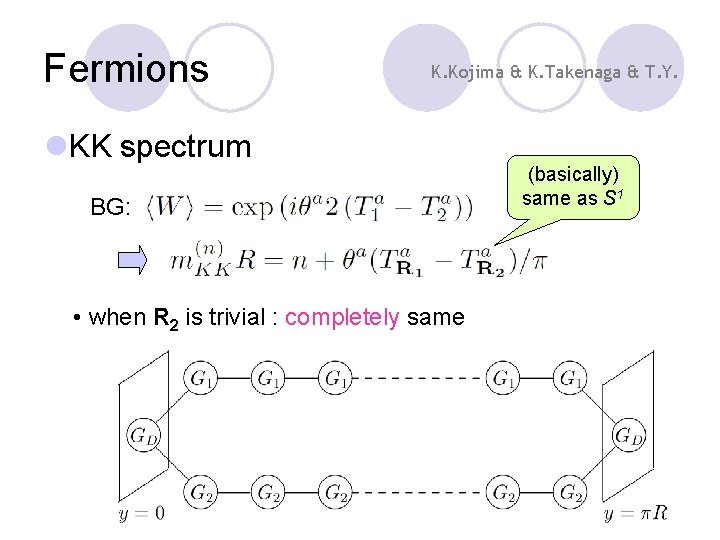
Fermions K. Kojima & K. Takenaga & T. Y. l. KK spectrum BG: • when R 2 is trivial : completely same (basically) same as S 1
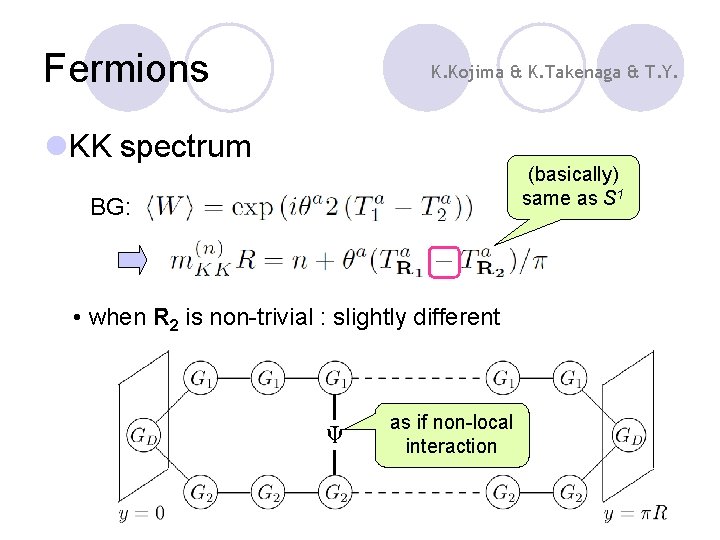
Fermions K. Kojima & K. Takenaga & T. Y. l. KK spectrum (basically) same as S 1 BG: • when R 2 is non-trivial : slightly different as if non-local interaction

Fermions K. Kojima & K. Takenaga & T. Y. l. KK spectrum BG: (basically) same as S 1 • when R 2 is non-trivial : slightly different the same as R 1*R 2 fermion in S 1, while it behaves as R 1*R 2 under Gdiag.
Plan • • • Introduction massless adjoint scalar Fermions Applications Summary

Applications K. Kojima & K. Takenaga & T. Y. The results in literatures can be easily reproduced, besides chiral fermions (on the branes). l. SU(5) • it is not easy to realize vacua where SU(5) is broken down to SM, as global minima. A. T. Davies & A. Mc. Lachlan (1989) • it is claimed the desired minimum can be realized w/ fermions : 5, 10 scalars : 5, 3*15, as a local minimum anti-periodic fermion V. B. Svetovoi & N. G. Khariton, (1986)

Summary • We propose a novel way to break GUT-symm. via the Hosotani mechanism. • adjoint scalars by diagonal embedding • chiral fermions on branes • It turns out KK spectra are basically the same as in S 1 models results in literatures are easily reproduced. • SU(5) GSM is not easy as global minima • model w/ desired vacuum as local minimum.

Summary lfuture works • SUSY and/or RS • doublet-triplet splitting • gauge coupling unification • concrete model building …
- Slides: 17