Grammars Derivations and Parsing Sample Grammar Simple arithmetic

Grammars, Derivations and Parsing

Sample Grammar • Simple arithmetic expressions (E) • Basis Rules: – A Variable is an E – An Integer is an E • Inductive Rules: – If E 1 and E 2 are Es, so is (E 1 + E 2) – If E 1 and E 2 are Es, so is (E 1 * E 2) • Examples: x, y, 3, 12, (x + y), (z * (x + y)), ((z * (x + y)) + 12)

Formal Definition of a Grammar G = (VN, VT, S, ), where VN, non-terminal symbols VT, terminal symbols S VN, start symbol = {( , ): V*VNV* and V*, V=(VT VN)} An element ( , ) of , is written as and is called a production rule or a rewrite rule

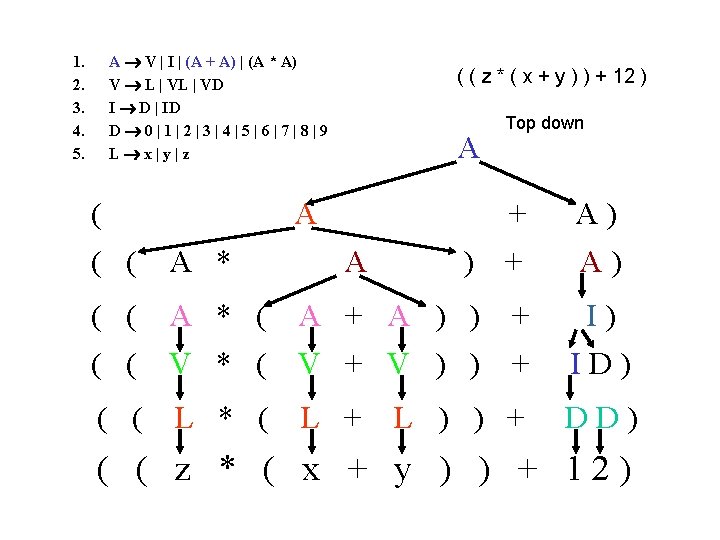
Sample Grammar Revisited 1. E V | I | (E + E) | (E * E) 2. V L | VD 3. I D | ID 4. D 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 5. L x | y | z VN: { E, V, I, D, L } VT: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, x, y, z } S=E : rules 1 -5

Another Simple Grammar • Symbols: P: phrase B: verb O: object A: article U: noun S: subject phrase V: verb phrase N: noun phrase • Rules: P SV S AU A a | the U monkey | banana | tree V BO B ate | climbs O N N AU

Backus-Naur Form (BNF) A traditional meta-language to represent grammars for programming languages • • Every non-terminal is enclosed in < and > is replaced with : : = I L | ID | IL L a|b|…|z D 0|1|…|9 <I> : : = <L> | <I><D> | <I><L> : : = a | b | … | z <D> : : = 0 | 1 | … | 9 WHY? Recall our language (C_DASH or : -)

Direct Derivative Let G = (VN, VT, S, ) be a grammar Let α, β (VN VT)* β is said to be a direct derivative of α, written α β, if there are strings 1 and 2 such that: α = 1 L 2, β = 1λ 2, L VN and L λ is a production of G We go from α to β using a single rule

Derivation Let G = (VN, VT, S, ) be a grammar Let α, ω (VN VT)* α is said to produce ω, or α reduces to ω, or ω is a derivation of α, written α + ω, if there are strings 1, …, n (n≥ 1) such that: α 1 2 … n-1 n ω We go from α to ω using several rules

Example of Derivation (I) 1. 2. 3. 4. 5. E V | I | (E + E) | (E * E) V L | VD I D | ID D 0|1|2|3|4|5|6|7|8|9 L x|y|z ( ( z * ( x + y ) ) + 12 ) ? E (E+E) ((E*E)+E) ((E*(E+E))+E) ((V*(V+V))+I) ( ( L * ( L + L ) ) + ID ) ( ( z * ( x + y ) ) + DD ) ( ( z * ( x + y ) ) + 12 ) How about: (x+2) ( 21 * ( x 4 + 7 ) ) 3*z 2 y

Example of Derivation (II) P SV S AU A a | the U monkey | banana | tree V BO B ate | climbs O N N AU a monkey ate a banana? P SV AUBO AUBN AUBAU a monkey ate a banana How about: the monkey climbs a tree a monkey ate a banana ate the tree

Context-Free Grammar A context-free grammar is a grammar with the following restriction: The relation is from VN to (VT VN)+ The left hand side of a production is a single non-terminal Context-free grammars generate context-free languages. With slight variations, essentially all programming languages are context-free languages. We will focus on context-free grammars

More Grammars Which ones are context-free? G 1 = (VN, VT, S, ), where: VN = {S, B} VT = {a, b, c} S=S = { S a. BSc , S abc , Ba a. B , Bb bb } G 3 = (VN, VT, S, ), where: VN = {S, A, B } VT = {a, b} S=S G 2 = (VN, VT, S, ), where: VN = {I, L, D} VT = {a, b, …, z, 0, 1, …, 9} S=I = { I L | ID | IL , L a|b|…|z, D 0|1|…|9 } = { S a. A , A a. A | b. B , B b. B | }

Grammar-generated Language If G is a grammar with start symbol S, a sentential form is any derivative of S A language L generated by a grammar G is the set of all sentential forms whose symbols are all terminals: L(G) = { | S + and VT*}

Example of Language Let G = (VN, VT, S, ), where: VN = {S, A, B} VT = {a, b} S=S = { S AB | ASB A a B b} What is L(G)? I IDD ILDD ILLDD LLLDD ab. LDD abc 12 Start by generating a few sentences (1 production, 2 productions, etc. ) Describe the general form in English

How About These? What is L(G)? G 1 = (VN, VT, S, ), where: VN = {S, B} VT = {a, b, c} S=S = { S a. BSc , S abc , Ba a. B , Bb bb } G 3 = (VN, VT, S, ), where: VN = {S, A, B } VT = {a, b} S=S G 2 = (VN, VT, S, ), where: VN = {I, L, D} VT = {a, b, …, z, 0, 1, …, 9} S=I = { I L | ID | IL , L a|b|…|z, D 0|1|…|9 } = { S a. A , A a. A | b. B , B b. B | }

Practice Exercises PE 1 Construct a grammar that generates strings of the form: 0 n 12 n ---------PE 2 Let G = {Vn, Vt, S, R} where Vn={S}, Vt={(, ), [, ]}, S=S, R={ S -> SS | () | (S) | [] | [S] }. Show that ([ [ [ ()() [ ][ ] ] ]([ ]) ]) belongs to L(G) by giving a derivation. ---------PE 3 Let G = {Vn, Vt, S, R} where Vn={S}, Vt={a, b}, S=S, R={ S -> a. Sa | b. Sb | epsilon }. What is L(G)? ---------PE 4 Construct a grammar to generate all strings starting with a letter and ending with a digit. ---------PE 5 Can you design a FSM that accepts the language 0 n 1 n? Why or why not?

Syntax Analysis: Parsing The parse of a sentence is the construction of a derivation for that sentence The parsing of a sentence results in • acceptance or rejection • if acceptance, then also a parse tree We are looking for an algorithm to parse a sentence and produce a parse tree Parsing checks that a sentence is grammatically correct (or belongs to the language)

Parser vs. Lexical Analyzer Lexical analyzer Input: symbols of length 1 Output: classified tokens Parser Input: classified tokens Output: syntactically correct program (or error) (Parse tree, or other suitable structure) A syntactically correct program will run. Will it do what you want? [a monkey ate a banana / a banana climbs the tree]

Parse Trees A parse tree is composed of • • interior nodes representing elements of VN leaf nodes representing elements of VT For each interior node N, the transition from N to its children represents the application of one production rule

Parse Tree Construction Top-down Start with the root (start symbol) Proceed downward to leaves using productions Bottom-up Start from leaves Proceed upward to the root Show top-down only here

Practice Exercises PE 1 Consider the grammar: P -> S V, S -> A U, A -> a | the, U -> monkey | banana | tree, V -> B O, B -> ate | climbs, O -> N, N -> A U. Build a top-down parse tree for the sentence: “a banana ate the monkey”. ---------PE 2 Consider the grammar: S -> a. S | A, A -> b | Ab. Build a top-down parse tree for the string: “aabb”.

Problems with Grammars Not all grammars are usable! • Ambiguous • Unproductive non-terminals • Unreachable rules

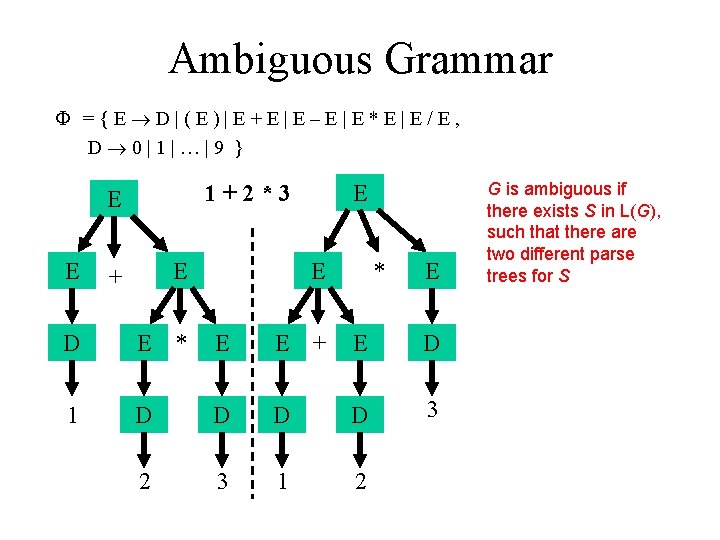
Ambiguous Grammar ={E D|(E)|E+E|E–E|E*E|E/E, D 0|1|…|9 } 1+2*3 E E D E + E * E E + * E E G is ambiguous if there exists S in L(G), such that there are two different parse trees for S D Multiple meanings: 1 D D 3 Precedence (1+2)*3≠ 1+(2*3) Associativity 2 3 1 2 (1 -2)-3≠ 1 -(2 -3)

Practice Exercises PE 1 A grammar is ambiguous if there exists a sentence in its language that can be derived by two different derivation trees. T or F: The grammar S -> a. S | Sb | epsilon is ambiguous ---------PE 2 Consider the grammar: S -> NP VP, NP -> N | A D N | D N, VP -> V | V NP, A -> a | the, N -> monkey | apple | matters | health, D -> nice | public | private, V -> looks | helps | matters | epsilon Show that the grammar is ambiguous using the string “public health matters”

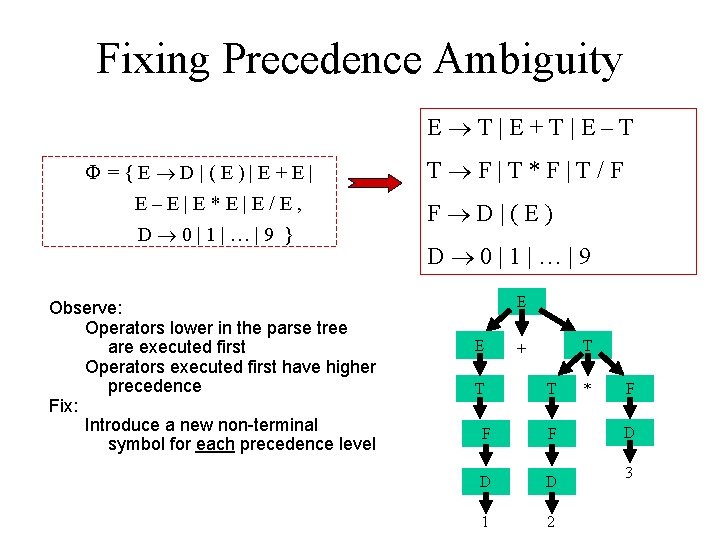
Fixing Precedence Ambiguity E T|E+T|E–T ={E D|(E)|E+E| E–E|E*E|E/E, D 0|1|…|9 } Observe: Operators lower in the parse tree are executed first Operators executed first have higher precedence Fix: Introduce a new non-terminal symbol for each precedence level T F|T*F|T/F F D|(E) D 0|1|…|9 E E T T + T F F D D 1 2 * F D 3

Adding the Power Operator E T|E+T|E–T T F|T*F|T/F F D|(E) D 0|1|…|9 E T | E+T | E T T P | T*P | T/P P F | F P F D | (E) D 0|1|…|9

Fixing Associative Ambiguity Left recursion/Left associativity E D|E D (3 2) 1 E E D D 3 2 1 Right recursion/Right associativity E D|D E 2 23 = 2 (3 2) E D E 2 D E 3 D 2

Practice Exercises PE 1 Consider the following ambiguous grammar: E -> E '=' E | E '--' | E '++' | E '<' E | E '>' E | '(' E ’)' | '4’ (the terminals are inside the quotation marks. Assume the order of precedence from highest to lowest is L 1: ++ and --, L 2: < and >, and L 3: =. Rewrite the grammar so it is no longer ambiguous. ---------PE 2 Consider the above grammar, and assume we add a new operator ‘&’, such that E -> E '&' E, and the precedence of the new operator is between L 2 and L 3. Modify the above grammar so it remains unambiguous and also accommodates the new operator.

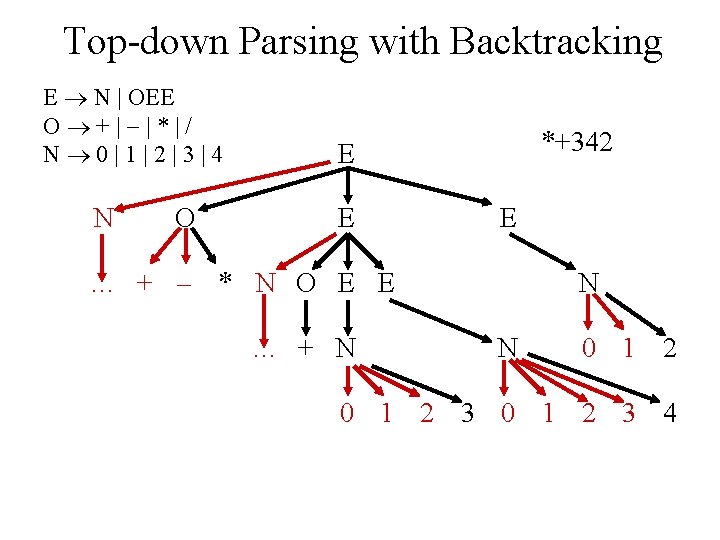
Top-down Parsing with Backtracking E N | OEE O +| |*|/ N 0|1|2|3|4 N O *+342 E E E … + * N O E E … + N N N 0 1 2 3 4 Prefix expressions associate an operator with the next two operands E. g. , *+324=(2+3)*4, *2+34=2*(3+4)

LL(1) Predictive Parsers Problem: Never know what production to try (and very inefficient) Solution: LL parser: parses input from Left to right, and constructs a Leftmost derivation of the sentence LL(k) parser uses k tokens of look-ahead LL(1) parsers: Somewhat restrictive, BUT Only need current non-terminal and next token to make parsing decision (hence, the name “predictive parser”) LL(1) parsers require LL(1) grammars

Simple LL(1) Grammars All rules have the form: A a 1 1 | a 2 2 | … | an n where ai (1 ≤ i ≤ n) is a terminal ai aj for i j i (1 ≤ i ≤ n) is a sequence of terminals and nonterminals, or is empty

Creating Simple LL(1) Grammars Why is this not a simple LL(1) grammar? E N | OEE O +| |*|/ N 0|1|2|3|4 How can we change it to simple LL(1)? By making all production rules of the form: A a 1 1 | a 2 2 | … | an n Thus, E 0 | 1 | 2 | 3 | 4 | +EE | *EE | /EE

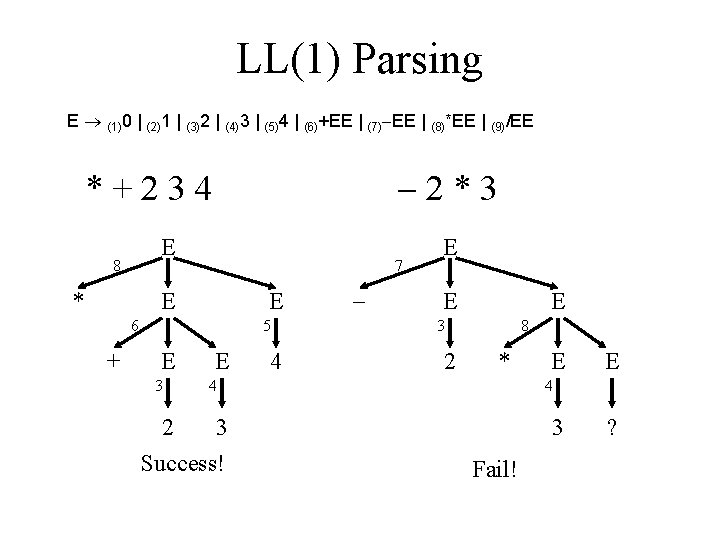
LL(1) Parsing E (1)0 | (2)1 | (3)2 | (4)3 | (5)4 | (6)+EE | (7) EE | (8)*EE | (9)/EE 2*3 *+234 E 8 * 7 E E 6 + 5 E 3 E 4 E E E 3 2 8 * 4 2 3 Success! E E 4 3 Fail! ?

Simple LL(1) Parse Table A parse table is defined as FOLLOWs: (V {#}) (VT {#}) {( , i), pop, accept, error} where is the right side of production number i # marks the end of the input string (# V) If A (V {#}) is the symbol on top of the stack and a (VT {#}) is the current input symbol, then: ACTION(A, a) = pop if A = a for a VT accept if A = # and a = # (a , i) which means “pop, then push a and output i” (A a is the ith production) error otherwise

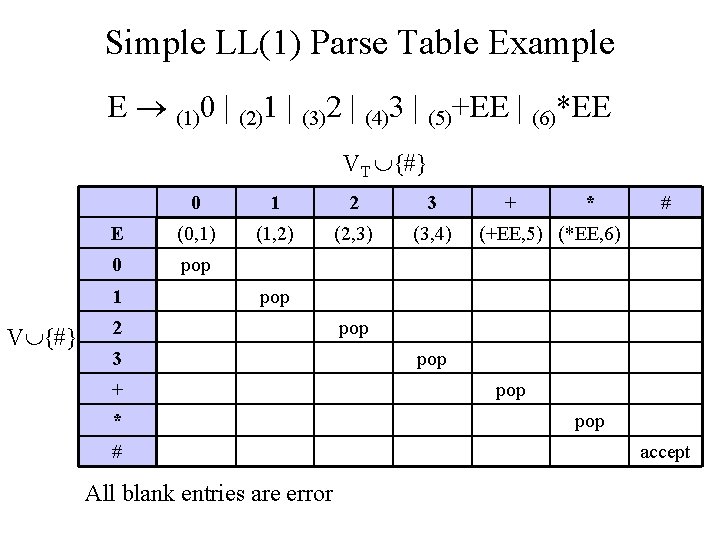
Simple LL(1) Parse Table Example E (1)0 | (2)1 | (3)2 | (4)3 | (5)+EE | (6)*EE VT {#} 0 1 2 3 E (0, 1) (1, 2) (2, 3) (3, 4) 0 pop 1 V {#} + * # (+EE, 5) (*EE, 6) pop 2 3 + * # All blank entries are error pop pop accept

Practice Exercises PE 1 Draw the parse table for the following LL(1) grammar: S -> a. A, A -> b. A | epsilon ---------PE 2 Draw the parse table for the following grammar: S -> the V O | a V O, V -> ate | climbs, O -> a N | the N, N -> monkey | banana | tree

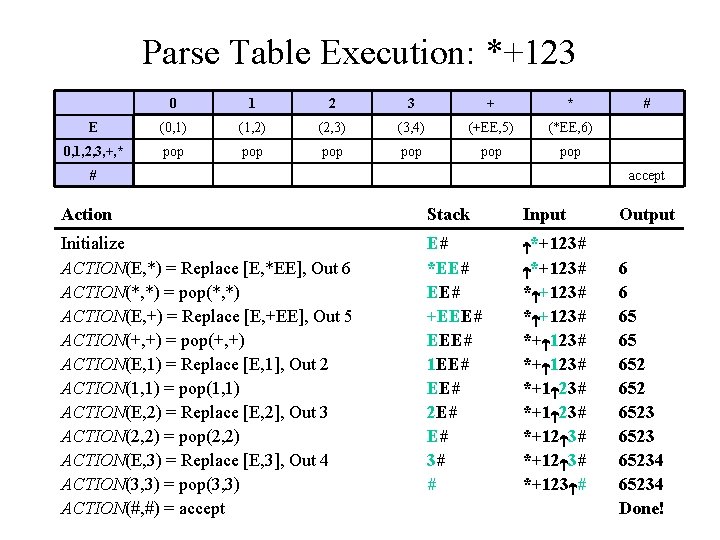
Parse Table Execution: *+123 0 1 2 3 + * E (0, 1) (1, 2) (2, 3) (3, 4) (+EE, 5) (*EE, 6) 0, 1, 2, 3, +, * pop pop pop # # accept Action Stack Input Initialize ACTION(E, *) = Replace [E, *EE], Out 6 ACTION(*, *) = pop(*, *) ACTION(E, +) = Replace [E, +EE], Out 5 ACTION(+, +) = pop(+, +) ACTION(E, 1) = Replace [E, 1], Out 2 ACTION(1, 1) = pop(1, 1) ACTION(E, 2) = Replace [E, 2], Out 3 ACTION(2, 2) = pop(2, 2) ACTION(E, 3) = Replace [E, 3], Out 4 ACTION(3, 3) = pop(3, 3) ACTION(#, #) = accept E# *EE# +EEE# 1 EE# 2 E# E# 3# # *+123# *+ 123# *+12 3# *+123 # Output 6 6 65 65 652 65234 Done!

Relaxing Simple LL(1) Restrictions Consider the following grammar E (1)N | (2)OEE O (3)+ | (4)* N (5)0 | (6)1 | (7)2 | (8)3 Not simple LL(1): rules (1) & (2) However: N leads only to {0, 1, 2, 3} O leads only to {+, *} {0, 1, 2, 3} {+, *} = We can distinguish between rules (1) and (2): If we see 0, 1, 2, or 3, we choose (1) If we see + or *, we choose (2)

Left-Factoring Consider the following grammar E T+E|T T int | int * T | ( E ) Not simple LL(1) and hard to predict since For T two productions start with int For E it is not clear how to predict Solution: Left-factoring Note: A grammar must be left-factored before it is used for predictive parsing

Left-Factoring Example Recall the grammar E T+E|T T int | int * T | ( E ) Factor out common prefixes of productions E TX X +E| T ( E ) | int Y Y *T|

FIRST For any , define: FIRST( ) = { | * and VT} Set of terminals that start strings derived from X A grammar is LL(1) if for all rules of the form A 1 | 2 | … | n then, FIRST( i) FIRST( j) = for i j (i. e. , the sets FIRST( 1), FIRST( 2), …, and FIRST( n) are pairwise disjoint)

FIRST Sets ─ Example Recall the grammar E TX T ( E ) | int Y FIRST sets FIRST( ( ) = { ( } FIRST( ) ) = { ) } FIRST( int ) = { int } FIRST( + ) = { + } FIRST( * ) = { * } X +E| Y *T| FIRST( T ) = { int, ( } FIRST( E ) = { int, ( } FIRST( X ) = { + } FIRST( Y ) = { * }

FOLLOW For any X, define: FOLLOW(X) = { t | S * X t and t VT} Set of terminals that start strings derived from start symbol through X Intuition If S is the start symbol then # FOLLOW(S) If X A B then FIRST(B) FOLLOW(A) and FOLLOW(X) FOLLOW(B) If B * then FOLLOW(X) FOLLOW(A)

FOLLOW Sets ─ Example Recall the grammar E TX T ( E ) | int Y X +E| Y *T| FOLLOW sets FOLLOW( + ) = { int, ( } FOLLOW( * ) = { int, ( } FOLLOW( ( ) = { int, ( } FOLLOW( E ) = { ), #} FOLLOW( X ) = { #, ) } FOLLOW( T ) = { +, ) , #} FOLLOW( ) ) = { +, ) , #} FOLLOW( Y ) = { +, ) , #} FOLLOW( int ) = { *, +, ) , #}

Revisiting Parse Tables Let A be a production rule For row A, in which column does go? In all columns t where t FIRST( ) In all columns t where is and t FOLLOW(A)

Practice Exercises PE 1 Draw the parse table for the following left-factored grammar: E -> T X, T -> (E ) | int Y, Y -> * T | epsilon, X -> + E | epsilon. ---------PE 2 Consider the following grammar: : S -> AB, A -> a. S | epsilon, B -> CD, C -> b. C | c, D -> d | epsilon. Is this grammar left-factored? If so, build a parse table for it. If not, explain why.

Recursive Descent Parsing

Setting Things Up Consider an arbitrary production S x. Ay. Sz and assume x is the current (top symbol), i. e. : x S (x. Ay. Sz, …)

Processing Non-terminal S Make a function for S as FOLLOWs: For S x. Ay. Sz Attempt to read an x from the input. If success, call method A. If success, attempt to read a y from the input. If success call method S. If success attempt to read a z from the input. If success, method S reports success! If any of the above attempts fails, report failure.

Preliminaries Consider the grammar E T+E|T T ( E ) | int * T Let: Token be the type of tokens (e. g. , INT, LPAREN, RPAREN, PLUS, TIMES) next be a reference to the next token

Recursive Descent Parser (1) Define boolean functions that check the token string for a match of A given token terminal boolean term(Token tok) { boolean result = next. equals(tok); next = next. Token(next); return result; } A given production of S (the nth) boolean Sn() { … } Any production of S: boolean S() { … } These functions advance next

Recursive Descent Parser (2) For production E T boolean E 1() { return T(); } For production E E T+E|T T ( E ) | int * T T+E boolean E 2() { return T() && term(PLUS) && E(); } For all productions of E (with backtracking) boolean E() { Token save; save = next; if (E 1()) return true; next = save; if (E 2()) return true; return false; }

Recursive Descent Parser (3) Functions for non-terminal T E T+E|T T ( E ) | int * T boolean T 1() { return term(LPAREN) && E() && term(RPAREN); } boolean T 2() { return term(INT) && term(TIMES) && T(); } boolean T 3() { return term(INT); } boolean T() { Token save; save = next; if (T 1()) return true; next = save; if (T 2()) return true; next = save; if (T 3()) return true; return false; }

Recursive Descent Parser (4) To start the parser E T+E|T T ( E ) | int * T Initialize next to point to first token Invoke E() Does not always work …

When Recursive Descent Does Not Work Consider a production S S a boolean S 1() { return S() && term(a); } boolean S() { return S 1(); } S() will get into an infinite loop A left-recursive grammar has a non-terminal S S + S for some Recursive descent does not work in such cases

Eliminating Left Recursion (1) Consider the left-recursive grammar S S | S generates all strings starting with a and FOLLOWed by a number of Can rewrite using right-recursion S S’ S’ S’ |

Eliminating Left Recursion (2) In general S S 1 | … | S n | 1 | … | m All strings derived from S start with one of 1, …, m and continue with several instances of 1, …, n Rewrite as S 1 S’ | … | m S’ S’ 1 S’ | … | n S’ |

General Left Recursion The grammar S A | A S is also left-recursive because S + S This indirect left-recursion can also be eliminated (flatten and remove)

Project 2 Given a legal Datalog program as input, parse it using a recursive-descent parser Also, a separate class The set of all string tokens found in facts or rules As you encounter string tokens in facts or rules, add the string to the set Use of domain will become clear later