Grammar Types The Chomsky Hierarchy BNF and Derivation

Grammar Types The Chomsky Hierarchy BNF and Derivation Trees Copyright © 2003 -2017 by Curt Hill

Introduction • We are now familiar with the notion of a grammar and the language that it covers • We should also have a grasp of automata • Next we wish to categorize grammars – This will be based on the forms that the productions take • We will start with the simplest and work up Copyright © 2003 -2017 by Curt Hill

Chomsky Hierarchy • Chomsky proposed an hierarchy of languages based on the strength of the rewriting rules • There are four – Type 0 through Type 3 • The hierarchy is based on the strength of the rewriting rules • Type 0 is strongest, 3 is weakest Copyright © 2003 -2017 by Curt Hill

Type 3 - Regular Languages • U n or U Wn • U and W are non-terminals and n is a terminal • A non-terminal may only be replaced by a terminal or non-terminal followed by a terminal • Regular expressions are of this type – Do you know about regular expressions? Copyright © 2003 -2017 by Curt Hill

Regular (3) • A b | A b. C | A Cd • The production must have only one nonterminal on the left • The right-hand side must be: – A terminal followed by a non-terminal – A non-terminal followed by a terminal • May not have a terminal non-terminal on right – Terminal may lead or follow but not both Copyright © 2003 -2017 by Curt Hill

Type 2 - Context Free • A a. Ny • Single non-terminal on left • Any number or arrangement of nonterminals and terminals on the right • Most programming languages are largely context free – The optional else in C/C++ is not Copyright © 2003 -2017 by Curt Hill

Type 1 - Context Sensitive • x. Uy xvy • Where U is a non-terminal and v is any sequence of terminals and/or non-terminals – x, y are terminals • U may be rewritten to v only in the context of x and y before and after • We may have another rule a. Ub aeb which is completely different replacement of U Copyright © 2003 -2017 by Curt Hill

Type 0 - Unrestricted • u v • Unrestricted both sides of the production may have non-terminals or terminals, but u cannot be empty • Unlike types 1 -3 u could be a terminal • Context is also important • Very powerful, very little work done with it Copyright © 2003 -2017 by Curt Hill

Language Hierarchies Type 3 Regular Type 2 Context Free Type 1 Context Sensitive Type 0 Unrestricted Copyright © 2003 -2017 by Curt Hill

Languages and Automata • Each of these languages corresponds to an automaton that can accept it • The weakest is a regular language, which can be accepted by a regular expression or finite state automaton • Later machines correspond to stronger languages • We have considered these automatons Copyright © 2003 -2017 by Curt Hill

Hierarchy Again Type Grammar Language Automata 3 Finite State Regular Finite 2 Context Free Pushdown 1 Context Sensitive Linear Bounded 0 Recursively enumerable Unrestricted Turing Machine Copyright © 2003 -2017 by Curt Hill

Again • We use regular (type 3) languages are used for lexical analyzers – The lexical analyzer is typically the frontend of a compiler • Most programing languages have a context-free grammar (type 2) – With a few ambiguities • Efficient algorithms exist to implement parsers for both of these – This cannot be said for type 0 and 1 Copyright © 2003 -2017 by Curt Hill

Derivation or parse trees • A multi-way tree where: – Each interior node is a non-terminal – Each leaf is a terminal – The start symbol is the root – Nested under each interior node is the RHS of the production, with the LHS being the node itself • This is a handy data structure for compilers and the like Copyright © 2003 -2017 by Curt Hill
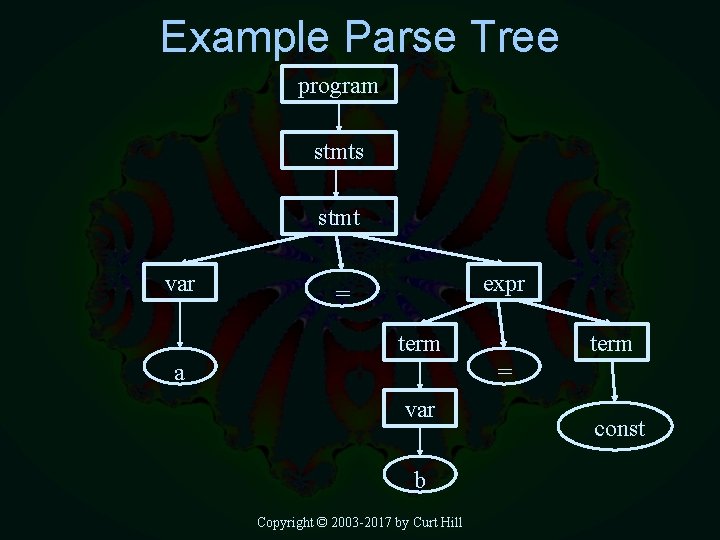
Example Parse Tree program stmts stmt var expr = term a term = var b Copyright © 2003 -2017 by Curt Hill const

Example • • Consider the following grammar V= {a, b, c, S} T = {a, b, c} P={ – S ab. S – S bc. S – S bb. S –S a – S cb } Copyright © 2003 -2017 by Curt Hill
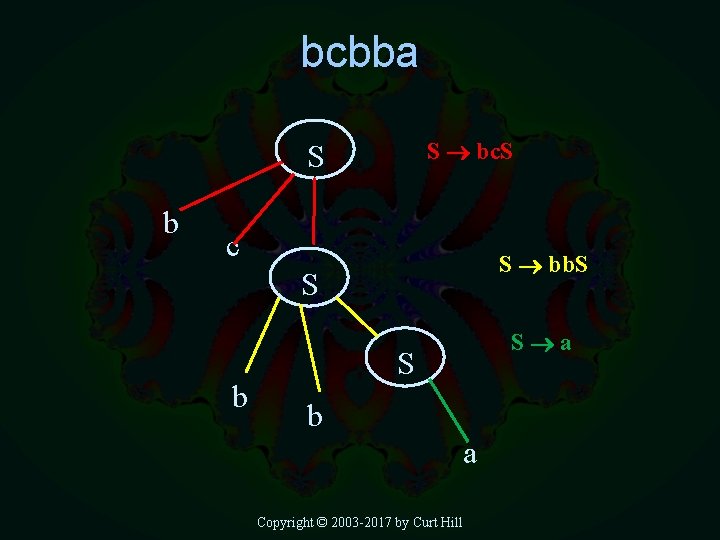
bcbba S bc. S S b c S bb. S S b S a S b a Copyright © 2003 -2017 by Curt Hill

Audience Participation • Lets try on the board • bcabbbbbcb • bbbcbba Copyright © 2003 -2017 by Curt Hill

John Backus • • Principle designer of FORTRAN Substantial contributions to Algol 60 Designed Backus Normal Form Eventually became a functional languages proponent • Turing award winner Copyright © 2003 -2017 by Curt Hill

BNF • John Backus defined FORTRAN with a notation similar to Context Free languages independent of Chomsky in 1959 • Peter Naur extended it slightly in describing ALGOL • Became known as BNF for Backus Normal Form or Backus Naur Form • Meta-language is the language that describes another language Copyright © 2003 -2017 by Curt Hill

Simplest notation • Form of productions: LHS : : = RHS • Where: – LHS is a non-terminal (context free grammars) – RHS is any sequence of terminals and non-terminals, including empty • There can be many productions with exactly the same LHS, these are alternatives • If the RHS contains the LHS, the rule is recursive Copyright © 2003 -2017 by Curt Hill

Notation • There is usually a simple way to distinguish terminals and non-terminals • Rosen and others enclose nonterminals in angle brackets – <if> : : = if ( <condition> ) <statement> else <statement> Copyright © 2003 -2017 by Curt Hill

Simple extensions • Some times there is an alternation symbol that allows us to only need one production with the same LHS, often the vertical bar – <sign> : : = + | - • Some times things enclosed in [ and ] are optional, they may be present zero or one times • Some times things enclosed in { and } may be present 1 or more times – Thus [{x}] allows zero or more x items Copyright © 2003 -2017 by Curt Hill

More • The extensions are often called EBNF • Syntax graphs are equivalent to EBNF • These tend to be more easy to read Copyright © 2003 -2017 by Curt Hill

Syntax Graphs • A circle represents a terminal – Reserved word or operator – No further definition • A rectangle represents a non-terminal – For statement or expression – Must be defined else where • An arrow represents the path between one item and another – The arrows may branch indicating alternatives • Recursion is also allowed Copyright © 2003 -2017 by Curt Hill
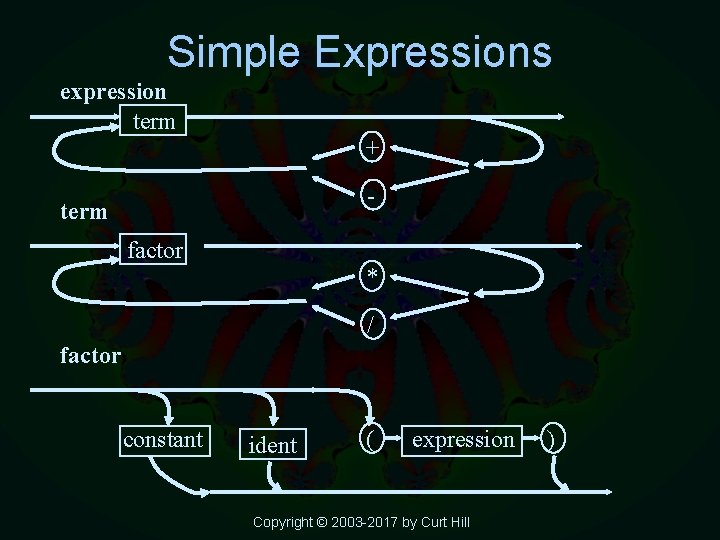
Simple Expressions expression term + - term factor * / factor constant ident ( expression Copyright © 2003 -2017 by Curt Hill )

Parse tree example • Trees are recursive • Every sub-tree is a tree itself • Consider the parse of: 2+5*(3 -4) – Using the previous syntax graph Copyright © 2003 -2017 by Curt Hill
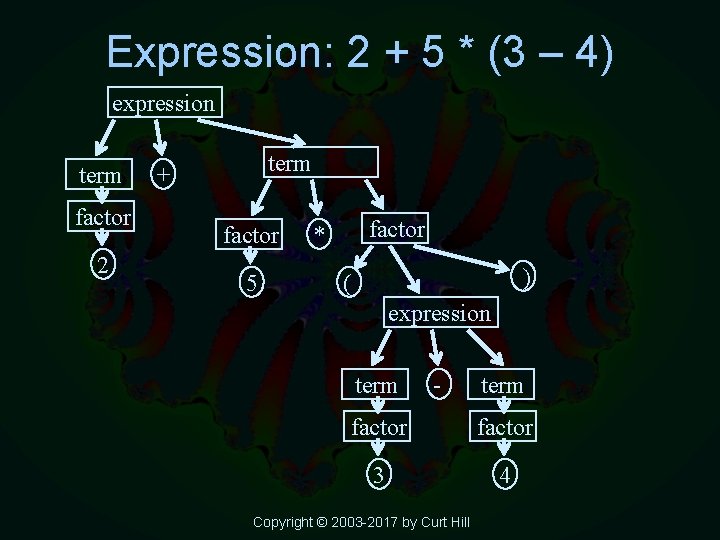
Expression: 2 + 5 * (3 – 4) expression term factor 2 term + factor 5 factor * ) ( expression term - term factor 3 4 Copyright © 2003 -2017 by Curt Hill

BNF is generative • A derivation is sentence generation • Leftmost derivation – Only the leftmost non-terminal can be rewritten – This is usually the kind of derivation used by compilers – The previous derivation was leftmost • There also rightmost derivations • The order of derivation does not affect the language defined Copyright © 2003 -2017 by Curt Hill

Example BNF productions <program> : : = <stmts> : : = <stmt> | <stmt> ; <stmts> <stmt> : : = <var> = <expr> <var> : : = a | b | c | d <expr> : : = <term> + <term> | <term> - <term> : : = <var> | const Copyright © 2003 -2017 by Curt Hill

Example Derivation <program> => => <stmts> <stmt> <var> = <expr> a = <term> + <term> a = <var> + <term> a = b + const Copyright © 2003 -2017 by Curt Hill

Finally • We should now have a handle on: – The connection of Chomsky hierarchy languages and automatons – Grammars of the form Chomsky proposed – BNF and other means to specify productions • What is left is to move into parsing – In particular table driven parsing Copyright © 2003 -2017 by Curt Hill
- Slides: 31