Grammar Application of a production A in a

Grammar

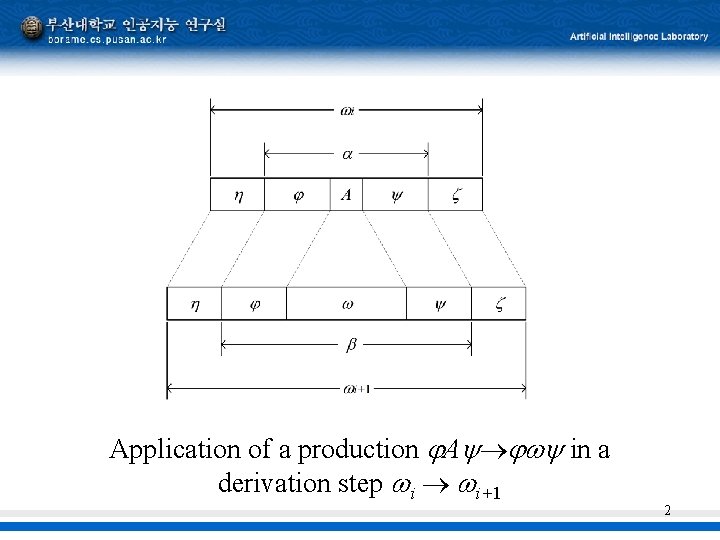
Application of a production A in a derivation step i i+1 2

Formal grammars (1/3) § Example : Let G 1 have N = {A, B, C}, T = {a, b, c} and the set of productions A CB BC A a. ABC b. B bb A ab. C bc c. C cc The reader should convince himself that the word akbkck is in L(G 1) for all k 1 and that only these words are in L(G 1). That is, L(G 1) = { akbkck | k 1}. 3

Formal grammars (2/3) § Example : Grammar G 2 is a modification of G 1: G 2: A CB BC A a. ABC b. B bb A ab. C b The reader may verify that L(G 2) = { akbk | k 1}. Note that the last rule, b. C b, erases all the C's from the derivation, and that only this production removes the nonterminal C from sentential forms. 4

Formal grammars (3/3) § Example : A simpler grammar that generates { akbk | k 1} is the grammar G 3 : G 3: S S a. Sb S ab A derivation of a 3 b 3 is S a. Sb aa. Sbb aaabbb The reader may verify that L(G 3) = { akbk | k 1}. 5

Type 0 Format of Productions φAψ→ φω ψ Remarks Unrestricted Substitution Rules 1 φAψ→ φω ψ, ω≠λ ∑→λ 2 A →ω, ω≠λ ∑→λ Context Sensitive Context Free 3 A→a. B A→a ∑→λ Right Linear Contracting Noncontracting Regular A→Ba A →a ∑→λ Left Linear The four types of formal grammars 6

Unrestricted Grammars(Type 0) Context-Sensitive Grammars(Type 1) § Definition : A context-sensitive grammar G = (N, T, P, ) is a formal grammar in which all productions are of the form φAψ→φωψ, ω≠ The grammar may also contain the production → , if G is a context-sensitive (type 1) grammar, then L(G) is a context-sensitive (type 1) language. 7

Context-Free Grammars (Type 2) § Definition : A context-free grammar G=(N, T, P, ) is a formal grammar in which all productions are of the form A→ω A∈N∪{ } ω∈(N∪T)*-{λ} The grammar may also contain the production →λ. If G is a context-free (type 2) grammar, then L(G) is a context-free (type 2) language. 8

Regular Grammars (Type 3) (1/2) § Definition : A production of the form A→a. B or A→a A∈N∪{∑} B∈N a∈T is called a right linear production. A production of the form A∈N∪{∑} B∈N A→Ba or A→a a∈T is a left linear production. A formal grammar is right linear if it contains only right linear productions, and is left linear if it contains only left linear production →λ. Left and right linear grammars are also known as regular grammars. If G is a regular (type 3) grammar, then L(G) is a regular (type 3) language. 9

Regular Grammars (Type 3) (2/2) § Example: A left linear grammar G 1 and a right linear grammar G 2 have productions as follows: G 1 : ∑ → 1 B G 2 : ∑ → B 1 ∑→ 1 A → 1 B A → B 1 B → 0 A B → A 0 A→ 1 The reader may verify that L(G 1) = (10)*1=1(01)*=L(G 2) 10

Ambiguity (1/2) § Example : Consider the context-free grammar G: S S SS S ab We see that the derivations correspond to different tree diagrams. The grammar G is ambiguous with respect to the sentence ababab: if the tree diagrams were used as the basis for assigning meaning to the derived string, mistaken interpretation could result. 11

Ambiguity (2/2) § Definition: A context-free grammar is ambiguous if and only if it generates some sentence by two or more distinct leftmost derivations. 12