Graf Teorisi Pregel Nehri http en wikipedia orgwikiLeonhardEuler

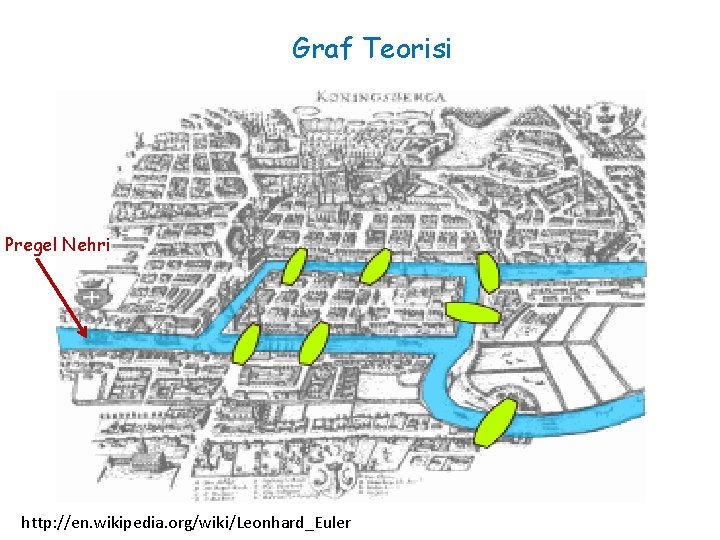
Graf Teorisi Pregel Nehri http: //en. wikipedia. org/wiki/Leonhard_Euler

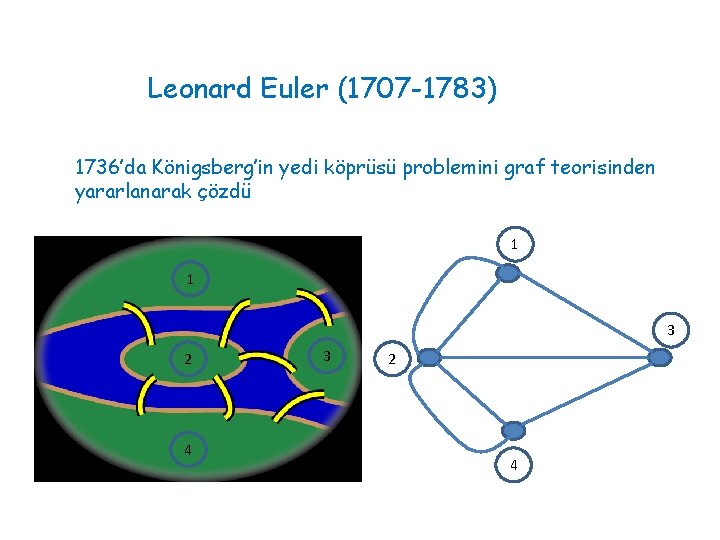
Leonard Euler (1707 -1783) 1736’da Königsberg’in yedi köprüsü problemini graf teorisinden yararlanarak çözdü 1 1 3 2 4

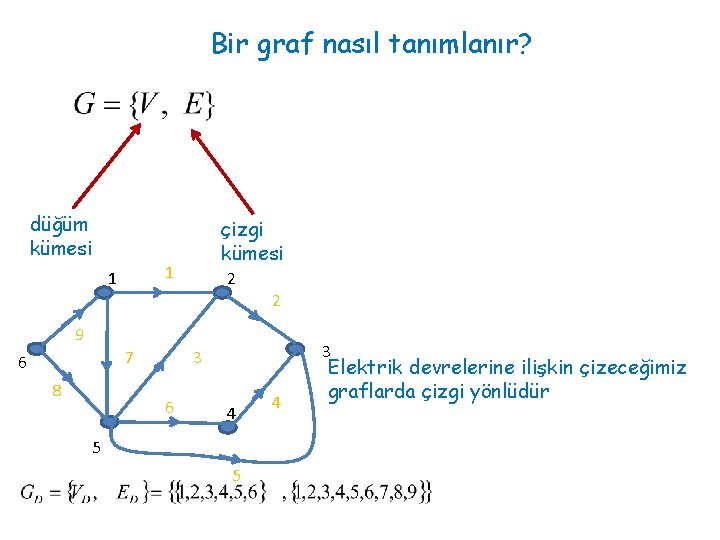
Bir graf nasıl tanımlanır? düğüm kümesi çizgi kümesi 1 1 2 2 9 7 6 8 3 3 6 4 5 5 4 Elektrik devrelerine ilişkin çizeceğimiz graflarda çizgi yönlüdür

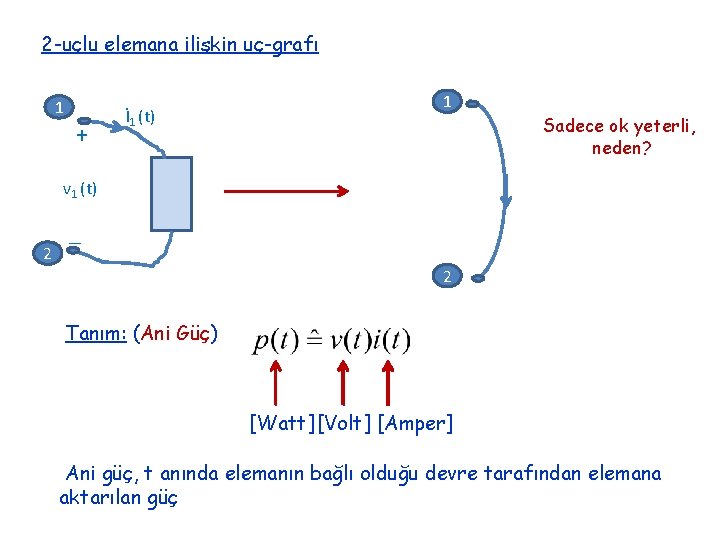
2 -uçlu elemana ilişkin uç-grafı 1 + İ 1 (t) 1 Sadece ok yeterli, neden? v 1 (t) 2 _ 2 Tanım: (Ani Güç) [Watt] [Volt] [Amper] Ani güç, t anında elemanın bağlı olduğu devre tarafından elemana aktarılan güç

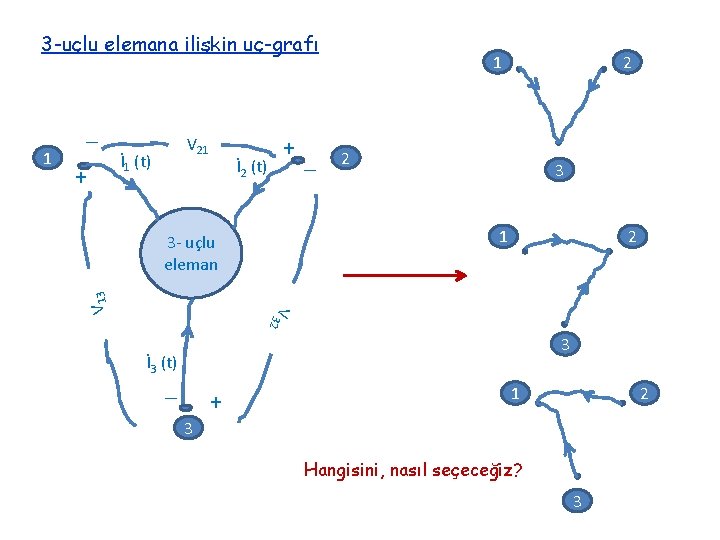
3 -uçlu elemana ilişkin uç-grafı _ V 21 İ 1 (t) + +_ İ 2 (t) 2 2 3 1 3 - uçlu eleman 2 V 3 V 13 1 1 2 3 İ 3 (t) _ + 1 2 3 Hangisini, nasıl seçeceğiz? 3

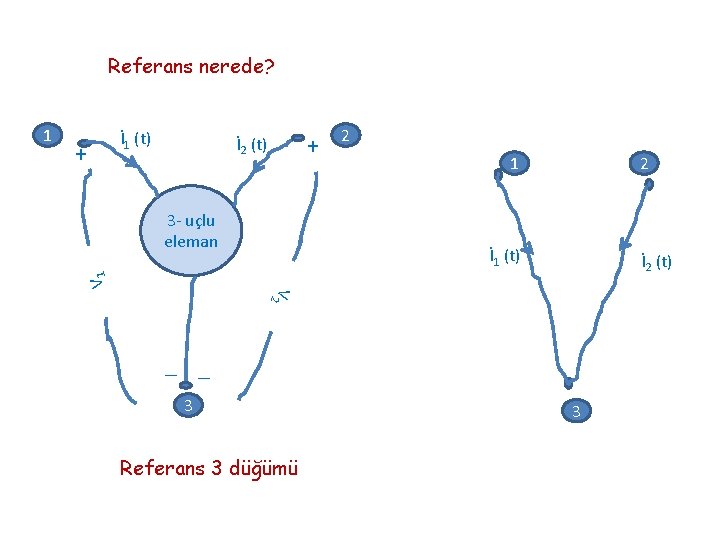
Referans nerede? + İ 1 (t) + İ 2 (t) 3 - uçlu eleman 2 1 2 İ 1 (t) İ 2 (t) V 1 1 V 2 _ _ 3 Referans 3 düğümü 3

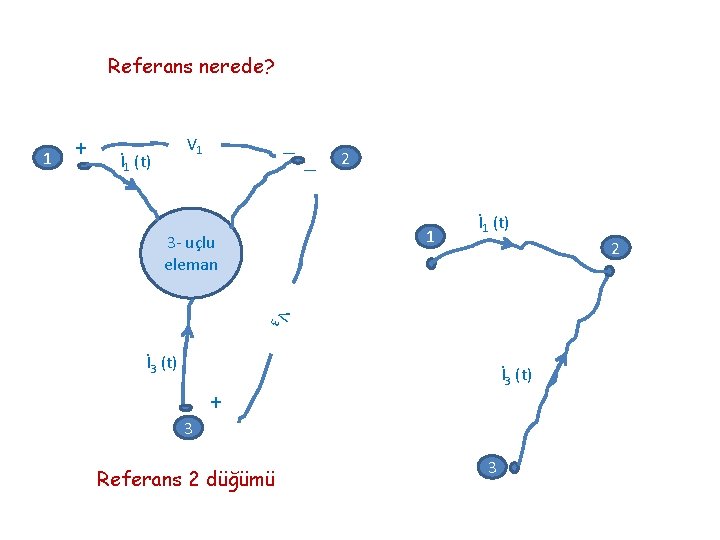
Referans nerede? 1 + _ V 1 İ 1 (t) _ 2 1 3 - uçlu eleman İ 1 (t) 2 V 3 İ 3 (t) + 3 Referans 2 düğümü 3

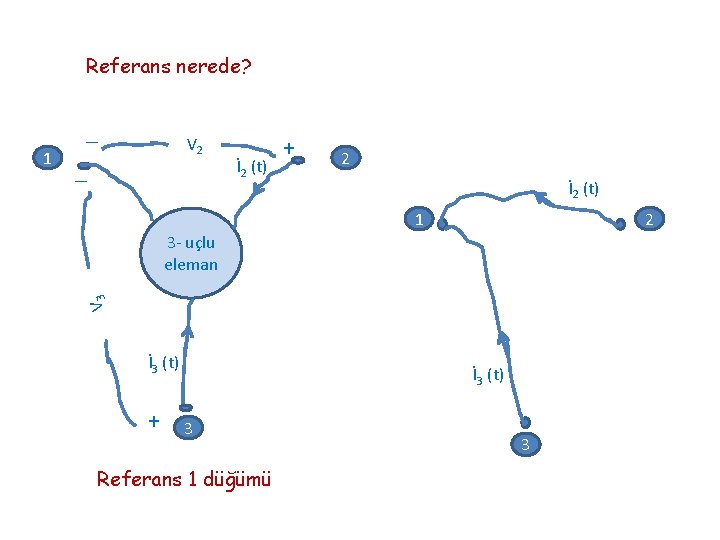
Referans nerede? _ V 2 _ İ 2 (t) + 2 İ 2 (t) 1 2 3 - uçlu eleman V 3 1 İ 3 (t) + İ 3 (t) 3 Referans 1 düğümü 3

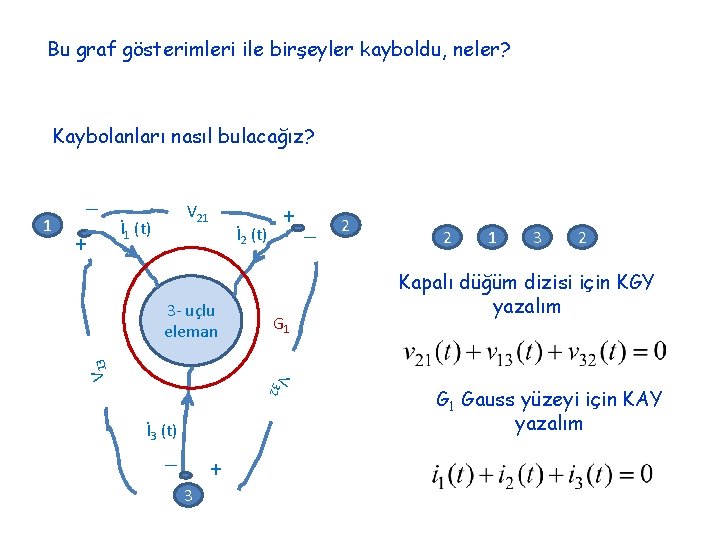
Bu graf gösterimleri ile birşeyler kayboldu, neler? Kaybolanları nasıl bulacağız? _ V 21 İ 1 (t) + +_ İ 2 (t) 3 - uçlu eleman G 1 V 3 V 13 1 2 İ 3 (t) _ + 3 2 2 1 3 2 Kapalı düğüm dizisi için KGY yazalım G 1 Gauss yüzeyi için KAY yazalım

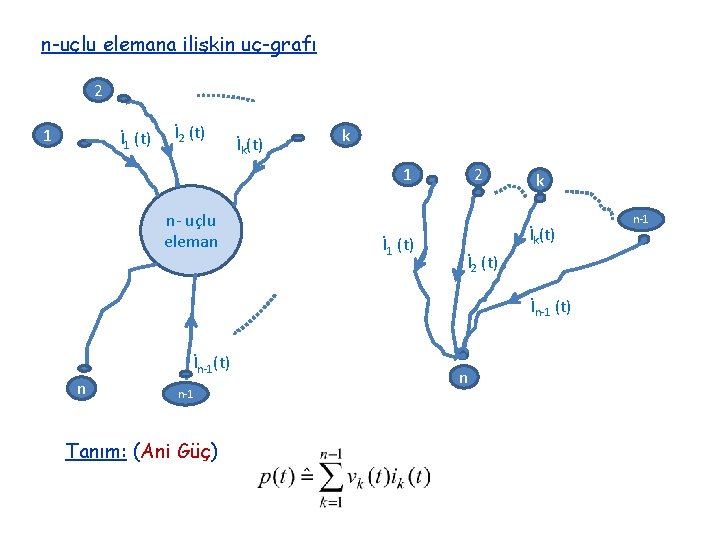
n-uçlu elemana ilişkin uç-grafı 2 1 İ 1 (t) İ 2 (t) İk(t) k 1 n- uçlu eleman İ 1 (t) 2 k İk(t) İ 2 (t) İn-1(t) n n-1 Tanım: (Ani Güç) n n-1

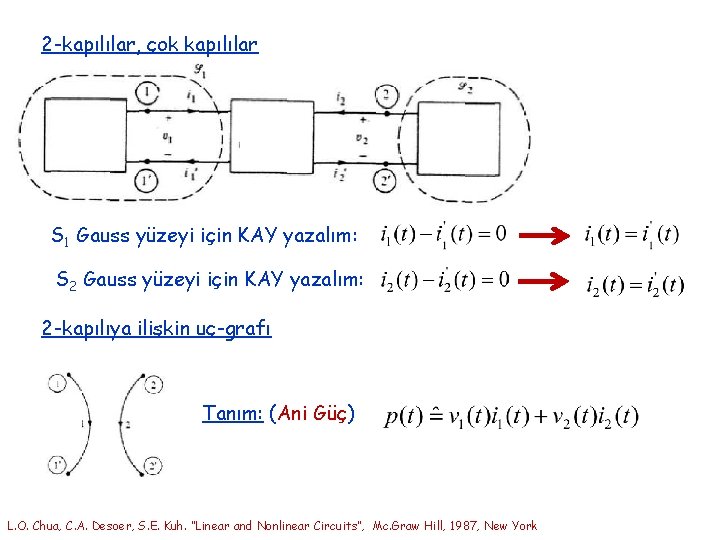
2 -kapılılar, çok kapılılar S 1 Gauss yüzeyi için KAY yazalım: S 2 Gauss yüzeyi için KAY yazalım: 2 -kapılıya ilişkin uç-grafı Tanım: (Ani Güç) L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits”, Mc. Graw Hill, 1987, New York

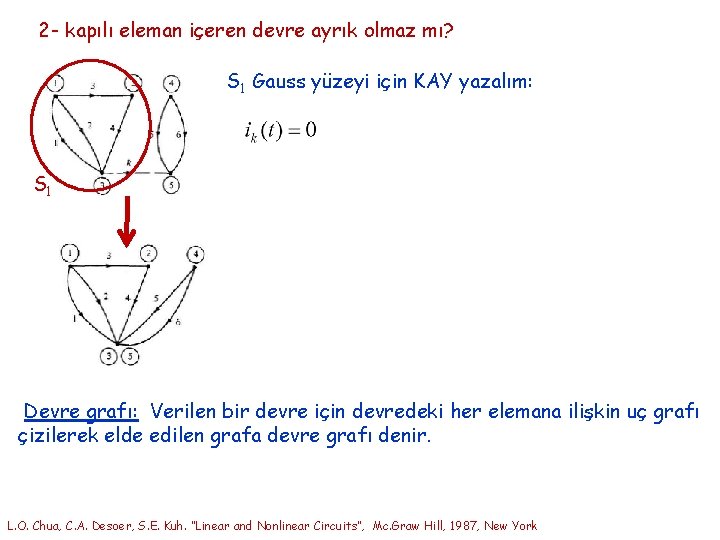
2 - kapılı eleman içeren devre ayrık olmaz mı? S 1 Gauss yüzeyi için KAY yazalım: S 1 Devre grafı: Verilen bir devre için devredeki her elemana ilişkin uç grafı çizilerek elde edilen grafa devre grafı denir. L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits”, Mc. Graw Hill, 1987, New York

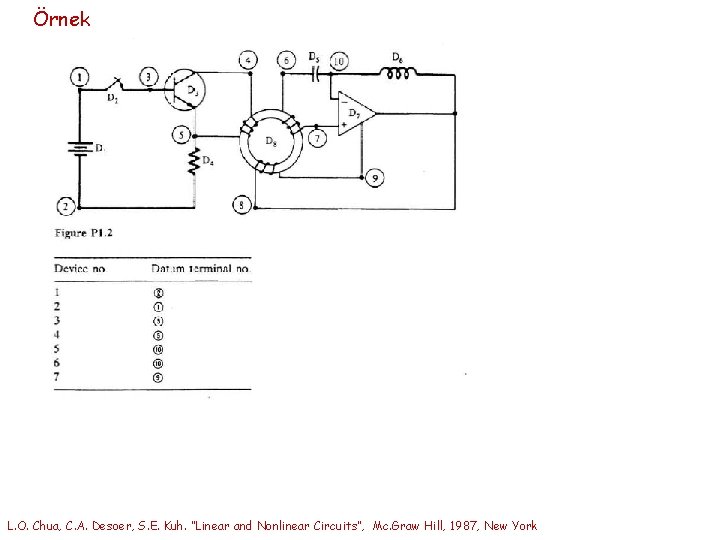
Örnek L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits”, Mc. Graw Hill, 1987, New York

Graf. Teorisine İlişkin Bazı Tanımlar Tanım: (Derece) Bir düğüme bağlı eleman sayısına o düğümün derecesi denir. Tanım: (Yol) G grafının aşağıdaki özellikleri sağlayan Gy alt grafına yol denir: • Gy ‘nin n çizgisi, n+1 düğümü vardır. • Gy ‘deki çizgiler e 1, e 2, . . . , en düğümler d 1, d 2, . . , dn+1 olmak üzere sırasıyla öyle numaralanabilirler ki ek çizgisinin düğümleri dk ve dk+1 olur. • d 1 ve dn+1 düğümlerinin dereceleri bir diğer düğümlerin dereceleri ikidir. Tanım: (Birleşik Graf) Verilen G grafında herhangi iki düğüm arasında en az bir yol varsa buna birleşik graf denir.

Tanım: (Çevre) G grafının aşağıdaki özellikleri sağlayan Ga alt grafına çevre denir: • Ga birleşik bir graftır. • Ga ‘daki bütün düğümlerin dereceleri ikidir. Tanım: (Ağaç) Birleşik bir G grafının aşağıdaki özellikleri sağlayan G T alt grafına ağaç denir: • GT , G’nin tüm düğümlerini kapsar. • GT çevre içermez. Tanım: (Dal) Ağaç’ın elemanlarına dal denir. Tanım: (Kiriş) G grafından GT çıkarıldığında geriye kalan alt grafa kirişler kümesi denir. Sonuç: nd düğümlü bir G grafında seçilecek dal sayısı nd-1 dir.

Tanım: ( Temel Çevreler Kümesi) ne elemanlı nd düğümlü birleşik bir G grafında GT seçilmiş bir ağaç olsun Bu ağacın belirlediği (ne –nd +1) adet kirişin her birisi diğer elemanları dal olmak üzere bir çevre tanımlar. Bu çevreye temel çevre, temel çevrelerin oluşturduğu kümeye de temel çevreler kümesi denir. Tanım: ( Kesitleme) Birleşik bir G grafının aşağıdaki özellikleri sağlayan G K alt grafına kesitleme denir: • G grafından GK çıkarıldığında geriye kalan graf iki parçadır. • GK ‘nın bir elemanını yerine koyarsak graf birleşik olur. Tanım: ( Temel Kesitlemeler Kümesi) ne elemanlı nd düğümlü birleşik bir G grafında GT seçilmiş bir ağaç olsun nd-1 tane dalın her biri diğer elemanları kiriş olmak üzere bir kesitleme tanımlar. Bu kesitlemeye temel kesitleme, temel kesitlemelerin oluşturduğu kümeye de temel kesitlemeler kümesi denir.

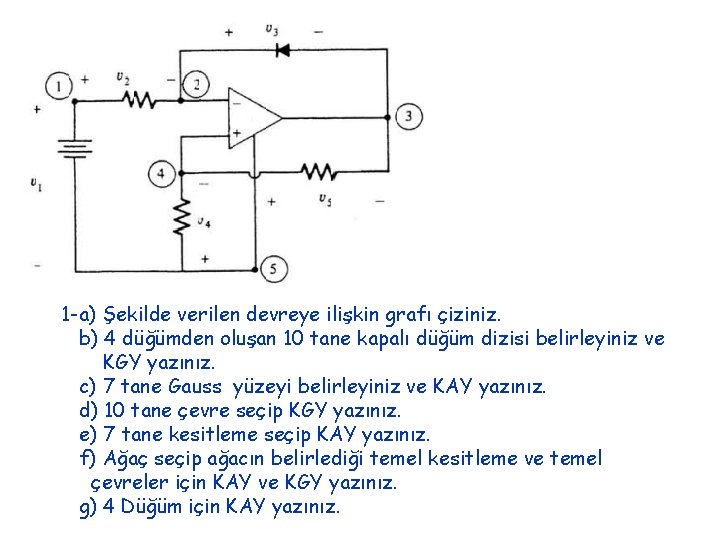
1 -a) Şekilde verilen devreye ilişkin grafı çiziniz. b) 4 düğümden oluşan 10 tane kapalı düğüm dizisi belirleyiniz ve KGY yazınız. c) 7 tane Gauss yüzeyi belirleyiniz ve KAY yazınız. d) 10 tane çevre seçip KGY yazınız. e) 7 tane kesitleme seçip KAY yazınız. f) Ağaç seçip ağacın belirlediği temel kesitleme ve temel çevreler için KAY ve KGY yazınız. g) 4 Düğüm için KAY yazınız.