Graf Oleh Devie Rosa Anamisa Didefinisikan dengan pasangan

Graf Oleh : Devie Rosa Anamisa

Didefinisikan dengan pasangan himpunan (V, E) yang dalam hal ini: V : himpunan berhingga dan tidak kurang dari simpul- simpul (vertices atau node), seperti: v 1, v 2, . . , vn. E : himpunan sisi (edges atau arcs) yang menghubungkan sepasang simpul, seperti: e 1, e 2, . . , en Dapat ditulis singkat notasi G(V, E). Notasi E = (Vi, Vj)

Contoh (a) V = { 1, 2, 3, 4} , jumlah simpul = |v| = 4 E = {(1, 2), (1, 3), (2, 4), (3, 4)} jumlah sisi = |E| = 4 (b) V= {1, 2, 3, 4} E = {(1, 2), (1, 3), (2, 4), (3, 1), (3, 4), (4, 3)} disebut himpunan ganda

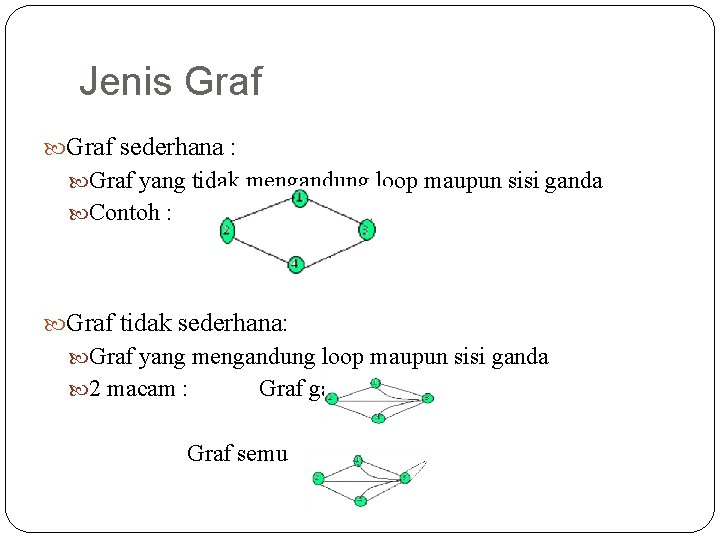
Jenis Graf sederhana : Graf yang tidak mengandung loop maupun sisi ganda Contoh : Graf tidak sederhana: Graf yang mengandung loop maupun sisi ganda 2 macam : Graf ganda Graf semu

Terminologi Graf Ketetanggaan (adjacent) Bila keduanya terhubung langsung , satu simpul. Vj bertetangga dengan Vk jika Ψe Є E sedemikian sehingga e = (Vj , Vk) Contoh : Simpul 1 bertetangga dengan simpul 2 dan simpul 3 tetapi tidak bertetangga dengan simpul 4.

Bersisian (incidency) Untuk sembarang sisi e =(Vj, Vk) dikatakan e bersisian dengan simpul Vj atau e bersisian dengan simpul Vk Contoh : Sisi (2, 3) bersisi dengan 2 dan 3 Sisi (2, 4) bersisi dengan 2 dan 4 Sisi (1, 2) tidak bersisi dengan 4

Simpul Terpencil (Isolated Vertex) Simpul yang tidak mempunyai sisi yang bersisi dengannya atau simpul yang tidak satupun bertetangga dengan simpul-simpul lainnya Contoh: Simpul 5 adalah simpul terpencil

Graf Kosong Graf menyatakan bahwa V tidak boleh kosong sedangkan E boleh kosong Graf yang himpunan sisinya merupakan himpunan kosong Contoh :

Derajat (Degree) Adalah jumlah sisi (E) yang bersisian dengan simpul tersebut Contoh : d(1) = d(4) =2 d(2) = d(3) = 3 d(5) = 0

Soal 1. Graf G =(V, E), tentukan himpunan vertex dan edge dari gambar berikut : 2. Graf semu berikut ini, tentukan himpunan vertex dan edge?

3. Gambarkan diagram untuk setiap graf G=(V, E) berikut: a. V = {A, B, C, D}, E={(A, B), (D, A), (C, D)} b. V = {a, b, c, d}, E = {(a, d), (a, f), (b, c), (b, f), (c, d)} c. V = {P 1, P 2, P 3, P 4, P 5}, E={(P 1, P 1), (P 2, P 3), (P 2, P 4), (P 3, P 2), (P 4, P 1), (P 5, P 4)}

4. Tentukan jumlah vertex dan edge pada gambar berikut:

5. Pada graf G=(V, E). (a) Terangkan G secara formal (himpunan verteks, himpunan edge) (b) Tentukan derajat dari setiap verteks dari G (c) jumlah derajat dr setiap vertex-vertex

6. Tentukan derajat setiap verteks: 7. Tentukan derajat setiap verteks:

8. Ada 7 kota (A, . . . , G) yang beberapa diantaranya dapat dihubungkan secara langsung dengan jalan darat. Hubungan hubungan langsung yang dapat dilakukan adalah sebagai berikut: A dengan B dan D B dengan D C dengan B E dengan F Buatlah graf yang menunjukkan keadaan di 7 kota tersebut!

9. Tentukan verteks, edge, titik-titik ujung masing garis!

10. Gambarkan graf G dengan titik V(G) = {v 1, v 2, v 3, v 4} dan garis E(G)={e 1, e 2, e 3, e 4, e 5} dengan titik ujung tersebut, sebagai berikut: