Graduate Institute of Electronics Engineering NTU CORDIC COordinate

Graduate Institute of Electronics Engineering, NTU CORDIC (COordinate Rotation DIgital Computer) For Advanced VLSI and VLSI Signal Processing Major Reference: Y. H. Hu, “CORDIC-based VLSI architectures for digital signal processing, ” IEEE Signal Processing Mag. , pp. 16 -35, July 1992. 2002/9/25 ACCESS IC LAB

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Outline v Introduction v Conventional CORDIC Algorithm v Enhancement of CORDIC v MVR-CORDIC Algorithm v EEAS-Based CORDIC Algorithm v Vector Rotational CORDIC Family 台灣大學 吳安宇 教授 2

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Introduction v Vector rotation is the kernel of various digital signal processing (DSP) applications, including v Digital filters: Ø Orthogonal digital filters, and adaptive lattice filters. v Linear transformation: Ø DFT, Chirp-Z transform, DHT, and FFT. v Matrix-based digital signal processing algorithms: Ø QR factorization, with applications to Kalman filtering and QR decomposition (QRD) based adaptive filtering. v Linear system solvers Ø such as Toeplitz and covariance system solvers, ……, etc. 台灣大學 吳安宇 教授 3

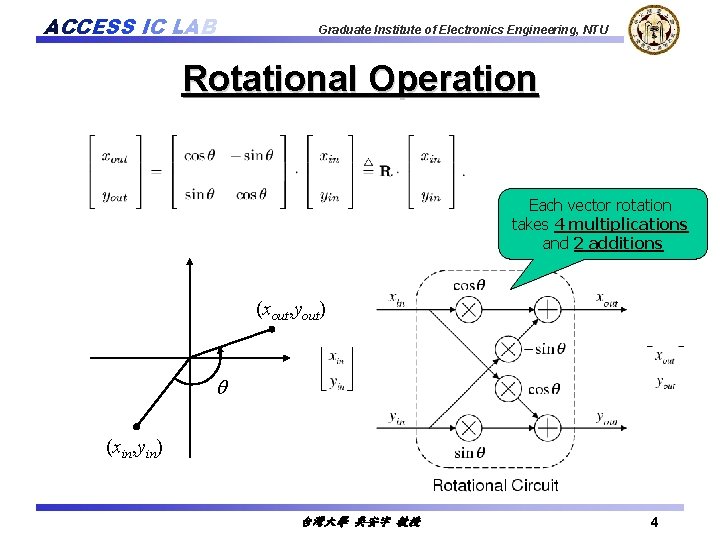
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Rotational Operation Each vector rotation takes 4 multiplications and 2 additions (xout, yout) q (xin, yin) 台灣大學 吳安宇 教授 4

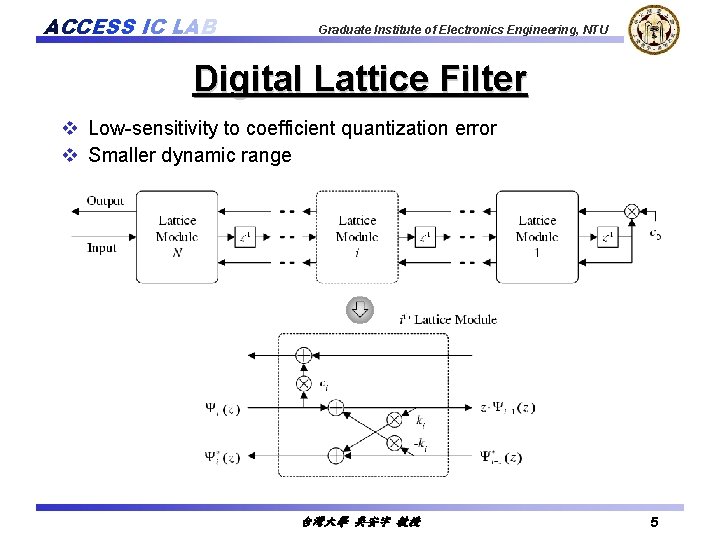
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Digital Lattice Filter v Low-sensitivity to coefficient quantization error v Smaller dynamic range 台灣大學 吳安宇 教授 5

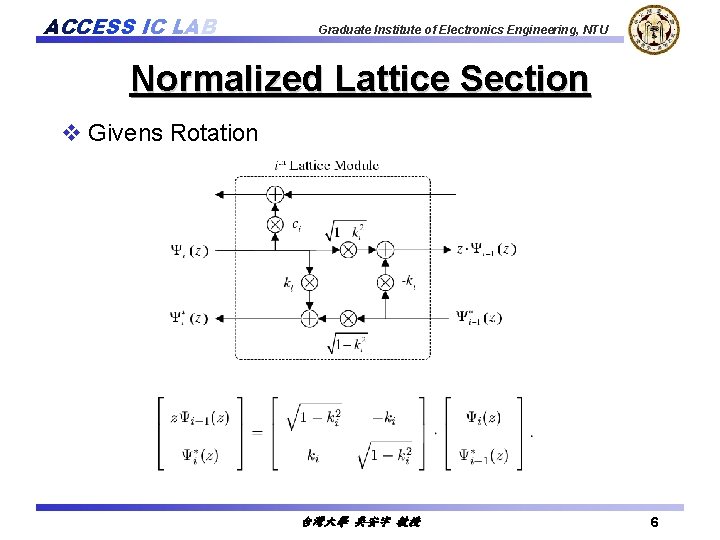
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Normalized Lattice Section v Givens Rotation 台灣大學 吳安宇 教授 6

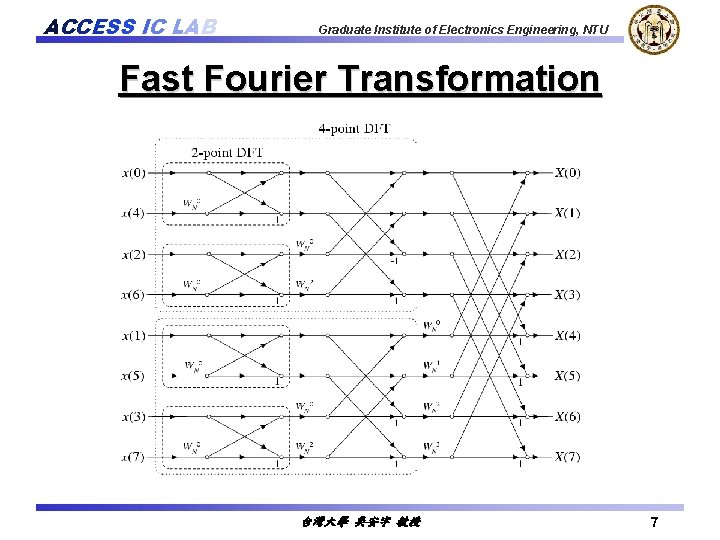
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Fast Fourier Transformation 台灣大學 吳安宇 教授 7

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Fast Fourier Transformation v Twiddle factor 台灣大學 吳安宇 教授 8

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Outline v Introduction ü Conventional CORDIC Algorithm v Enhancement of CORDIC v MVR-CORDIC Algorithm v EEAS-Based CORDIC Algorithm v Vector Rotational CORDIC Family 台灣大學 吳安宇 教授 9

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Basic Concept of CORDIC Operation v. To decompose the desired rotation angle (θ) into the weighted sum of a set of predefined elementary rotation angles (θ(i), I=0, 1, 2, …W) v. Such that the rotation through each of them can be accomplished with simple shift-and-add operation. 台灣大學 吳安宇 教授 10

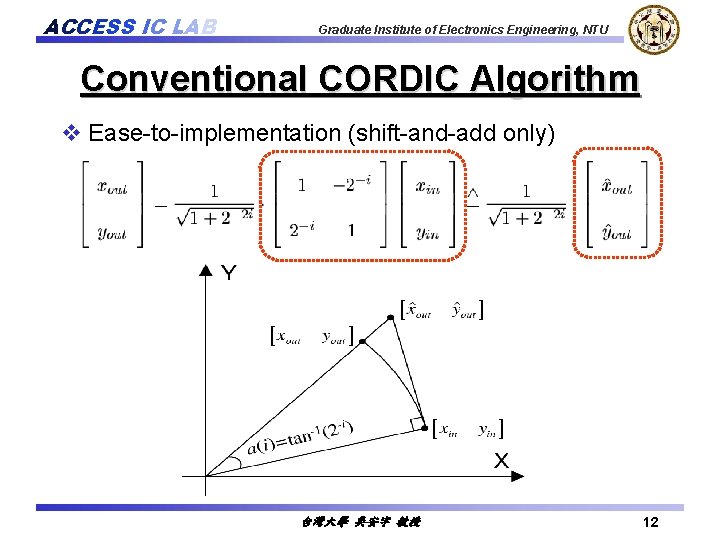
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Conventional CORDIC Algorithm where 台灣大學 吳安宇 教授 11

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Conventional CORDIC Algorithm v Ease-to-implementation (shift-and-add only) 台灣大學 吳安宇 教授 12

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Elementary Angle Set of Conventional CORDIC with N=W=8 台灣大學 吳安宇 教授 13

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Conventional CORDIC Algorithm l Sequentially performing of sub-angles, a(i) v Example: v Rotation angle: q = p/8 = 0. 3927 V(1) V(3) V(4) V(2) V(0) 台灣大學 吳安宇 教授 14

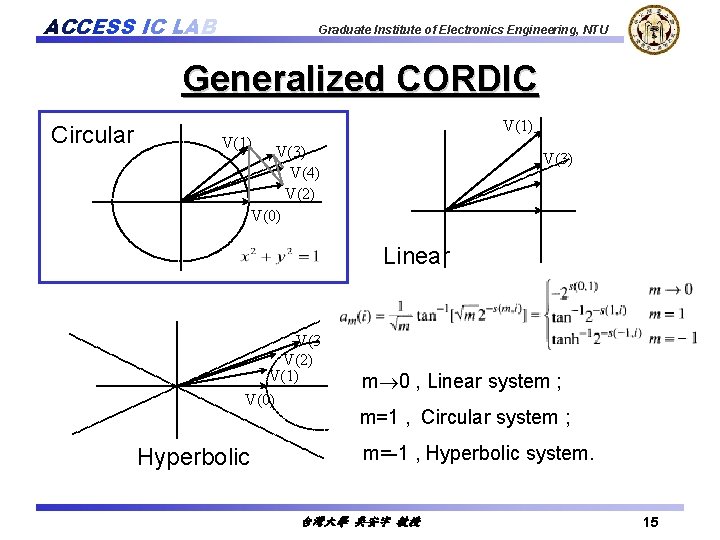
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Generalized CORDIC Circular V(1) V(3) V(4) V(2) V(0) V(3) Linear V(3) V(2) V(1) V(0) Hyperbolic m 0 , Linear system ; m=1 , Circular system ; m=-1 , Hyperbolic system. 台灣大學 吳安宇 教授 15

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Summary of CORDIC Algorithm v Both micro-rotation and scaling phases 台灣大學 吳安宇 教授 16

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Modes of CORDIC Operations v Vector rotation mode (θ is given) v The objective is to compute the final vector v Usually , we set z(0)= θ after the N-th iteration Rotational Sequence θ = sign of z(i) 台灣大學 吳安宇 教授 17

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Usage of Vector Rotation Mode v In below situations, one may choose to evaluate angle by computing the rotational sequence in advance (off-line). v For many DSP problem, v The same , is know in advance (e. g. , twiddle factor) will be used over and over. v Store the corresponding set of , instead of , in the memory. v A particular advantage is that there will be no need to implement the angle updating formula resulting in a one-third cost saving of hardware. 台灣大學 吳安宇 教授 18

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Modes of Operations (cont’d) v Angle accumulation mode (θ is not given) v Objective is to rotate the given initial vector back to x-axis, and the angle can be accrued. V(0) θ X-axis V(1) v Set z(0) = 0; v Rotational Sequence v i = - sign x(i)y(i) 台灣大學 吳安宇 教授 19

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Rotational Sequence v The selection criteria for v. s. are: v Note that the set of can be regard as an alternative representation of the rotation angle . v Hence, even in the angle accumulation mode, often it is not necessary to explicitly compute 台灣大學 吳安宇 教授 20

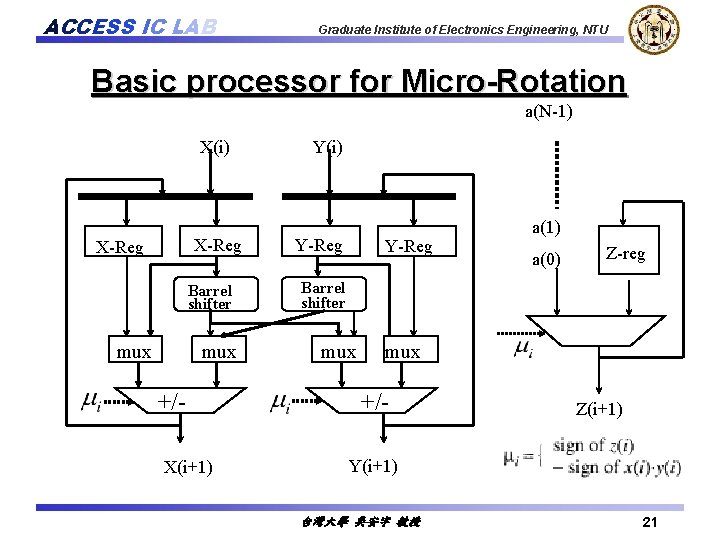
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Basic processor for Micro-Rotation a(N-1) X(i) X-Reg Barrel shifter mux +/X(i+1) Y(i) Y-Reg a(1) a(0) Z-reg Barrel shifter mux +/- Z(i+1) Y(i+1) 台灣大學 吳安宇 教授 21

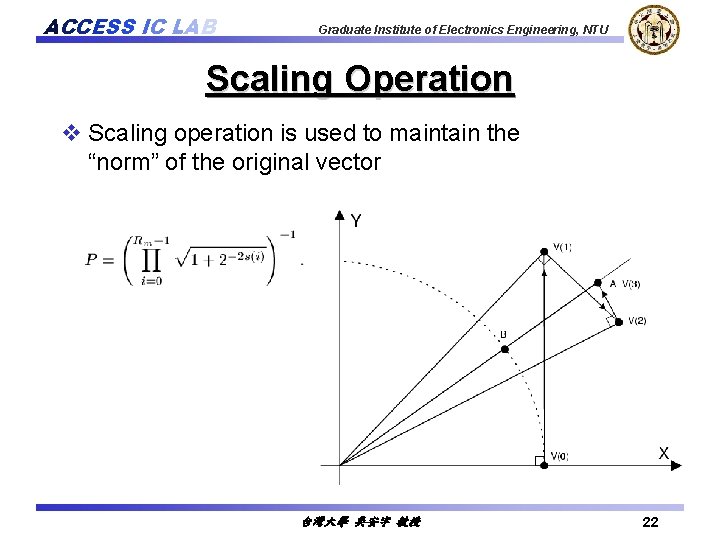
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Scaling Operation v Scaling operation is used to maintain the “norm” of the original vector 台灣大學 吳安宇 教授 22

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Conventional Scaling Operation 台灣大學 吳安宇 教授 23

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Selective Scaling Operation v Combine Type-I and Type-II scaling operation by featuring v Complementary distribution v Off-line operation 台灣大學 吳安宇 教授 24

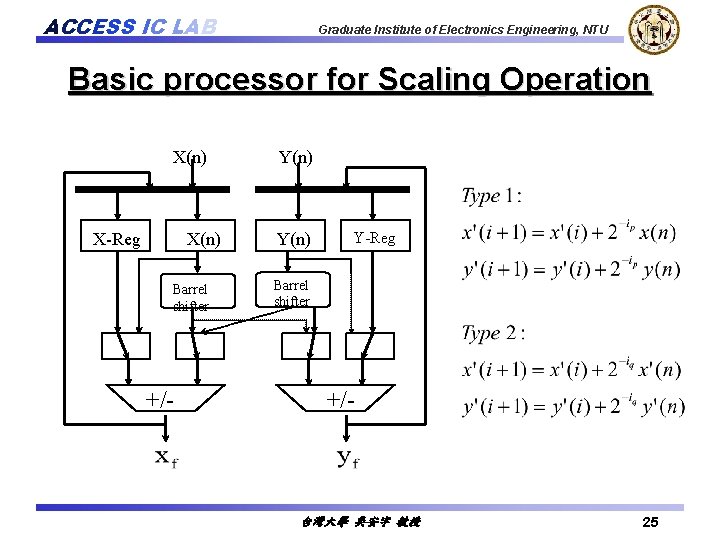
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Basic processor for Scaling Operation X(n) X-Reg X(n) Barrel shifter +/- Y(n) Y-Reg Barrel shifter +/- 台灣大學 吳安宇 教授 25

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Advantages and disadvantages -Simple Shift-and-add Operation. (2 adders+2 shifters v. s. 4 mul. +2 adder) -Small area. -It needs n iterations to obtain n-bit precision. -Slow carry-propagate addition. -Area consuming shifts (Barrel Shifter) 台灣大學 吳安宇 教授 26

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Enhancement of CORDIC v Architecture v. Pipelined Architecture v. Faster Adder (CSA) v Algorithm v. Radix-4 CORDIC v. MVR-CORDIC v. EEAS-CORDIC 台灣大學 吳安宇 教授 27

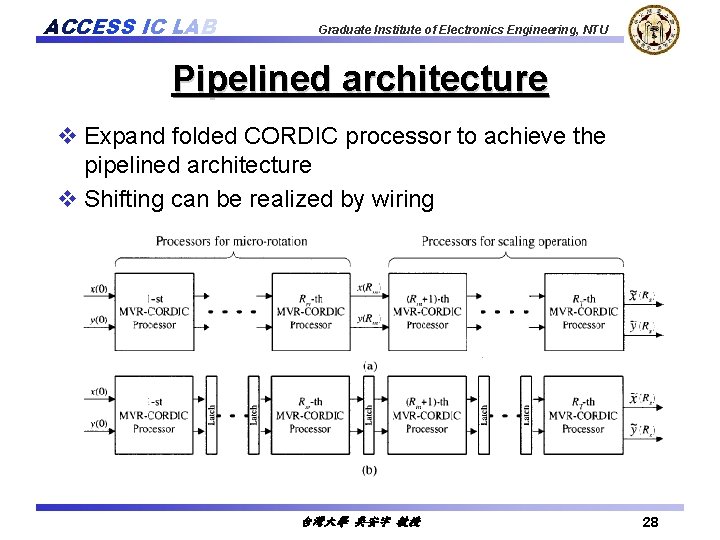
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Pipelined architecture v Expand folded CORDIC processor to achieve the pipelined architecture v Shifting can be realized by wiring 台灣大學 吳安宇 教授 28

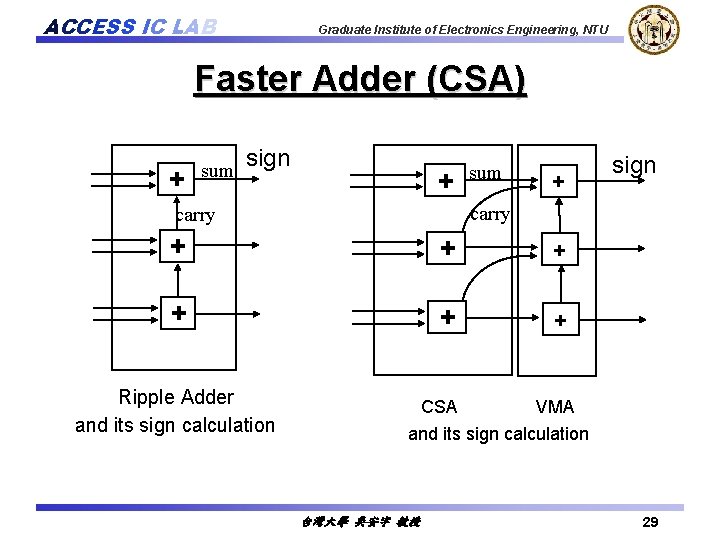
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Faster Adder (CSA) + sum sign + sum + carry + + + Ripple Adder and its sign calculation sign CSA VMA and its sign calculation 台灣大學 吳安宇 教授 29

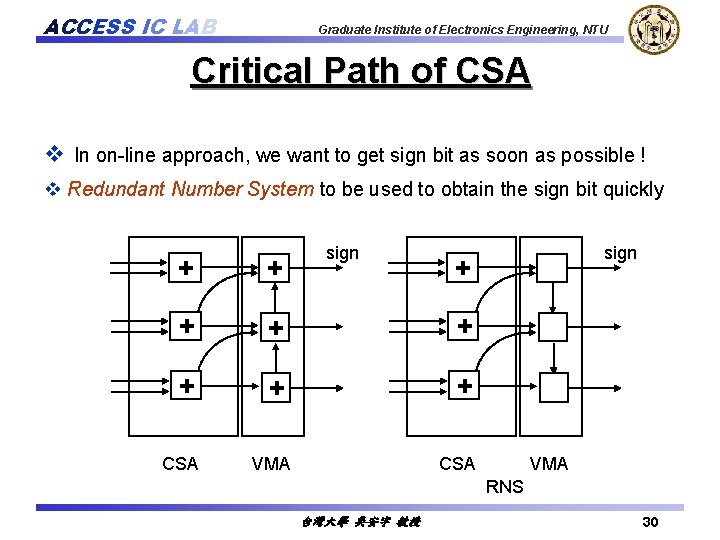
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Critical Path of CSA v In on-line approach, we want to get sign bit as soon as possible ! v Redundant Number System to be used to obtain the sign bit quickly sign + + + + CSA VMA sign + CSA VMA RNS 台灣大學 吳安宇 教授 30

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Radix-4 CORDIC v Reduce Iteration Numbers v. High radix CORDIC. (e. g. Radix-4, Radix-8) v 1 stage of Radix-4 = two stages of Radix-2 v. Faster computation at higher cost v Employ the Radix-4 micro-rotations to v. Reduce the stage number. v But Km may not be constant. 台灣大學 吳安宇 教授 31

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Outline v Introduction v Conventional CORDIC Algorithm v Enhancement of CORDIC ü Modified Vector Rotation (MVR)-CORDIC Algorithm v EEAS-Based CORDIC Algorithm v Vector Rotational CORDIC Family 台灣大學 吳安宇 教授 32

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Modification of CORDIC Algorithm v Skip some micro-rotation angles v For certain angles, we can only reduce the iteration number but also improve the error performance. v For example, q=p/4 Conventional CORDIC xm= 7. 2*10 -3 MVR-CORDIC xm= 0 台灣大學 吳安宇 教授 33

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Modification of CORDIC Algorithm v Repeat some micro-rotation angles v Each micro-rotation angle can be performed repeatedly v For example, q =p/2: execute the micro-rotation of a(0) twice v Confine the number of micro-rotations to Rm v In conventional CORDIC, number of iteration=W v In the MVR-CORDIC, Rm << W v Hardware/timing alignment 台灣大學 吳安宇 教授 34

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Modification of CORDIC Algorithm v With above three modification where § s(i) {0, 1, 2, …, W} is the rotational sequence that determines the micro-rotation angle in the ith iteration § a(i) {-1, 0 , 1} is the directional sequence that controls the direction of the ith micro-rotation 台灣大學 吳安宇 教授 35

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Elementary Angle Set of Conventional CORDIC with N=W=8 台灣大學 吳安宇 教授 36

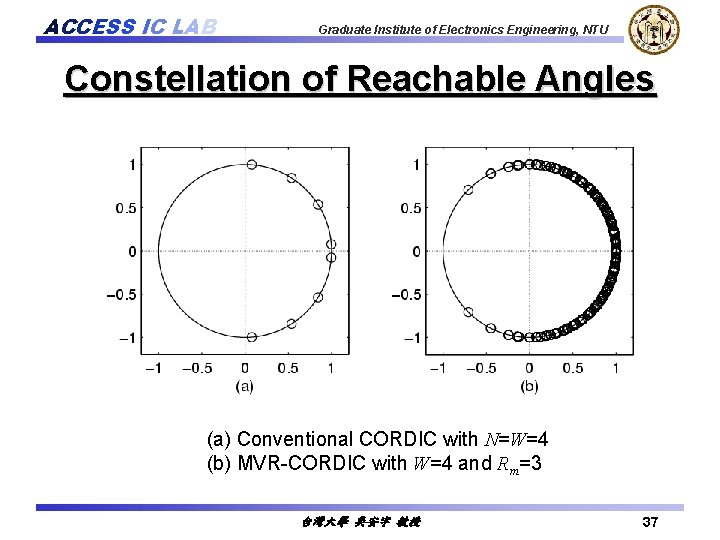
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Constellation of Reachable Angles (a) Conventional CORDIC with N=W=4 (b) MVR-CORDIC with W=4 and Rm=3 台灣大學 吳安宇 教授 37

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Summary of MVR-CORDIC Algorithm v Both micro-rotation and scaling phases 台灣大學 吳安宇 教授 38

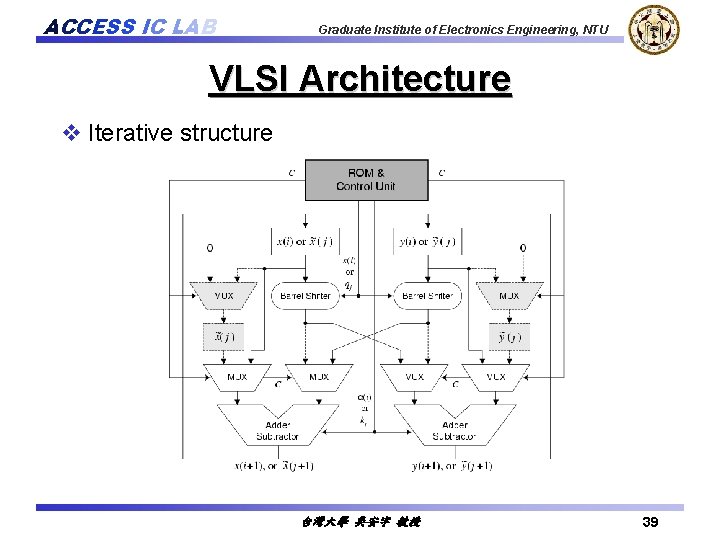
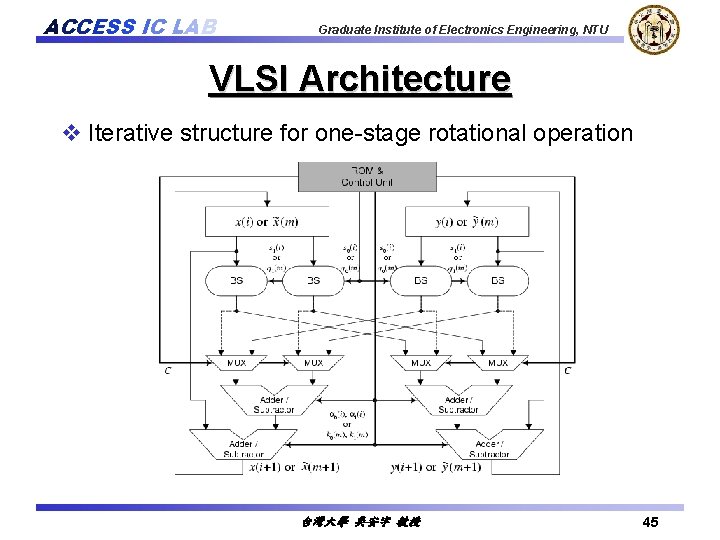
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU VLSI Architecture v Iterative structure 台灣大學 吳安宇 教授 39

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Outline v Introduction v Conventional CORDIC Algorithm v Enhancement of CORDIC v MVR-CORDIC Algorithm ü EEAS-Based CORDIC Algorithm v Vector Rotational CORDIC Family 台灣大學 吳安宇 教授 40

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Extended Elementary Angle Set (EEAS) v Apply relaxation on EAS of v EAS is comprised of arctangent of single singedpower-of-two (SPT) term v Effective way to extend the EAS is to employ more SPT terms 台灣大學 吳安宇 教授 41

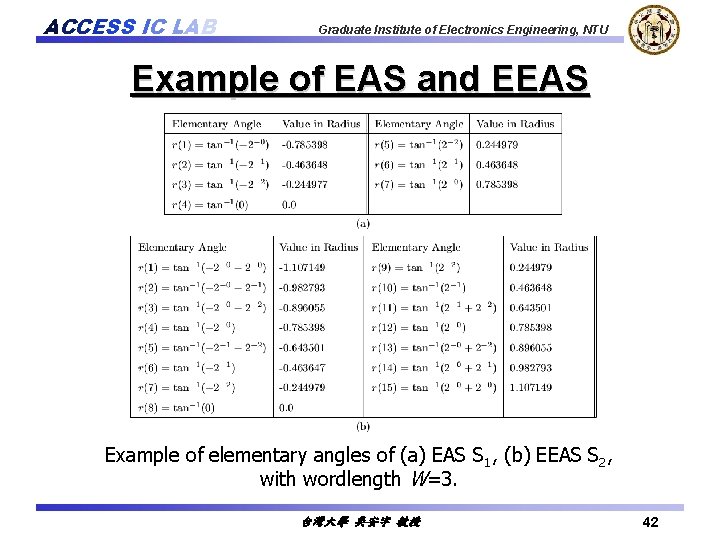
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Example of EAS and EEAS Example of elementary angles of (a) EAS S 1, (b) EEAS S 2, with wordlength W=3. 台灣大學 吳安宇 教授 42

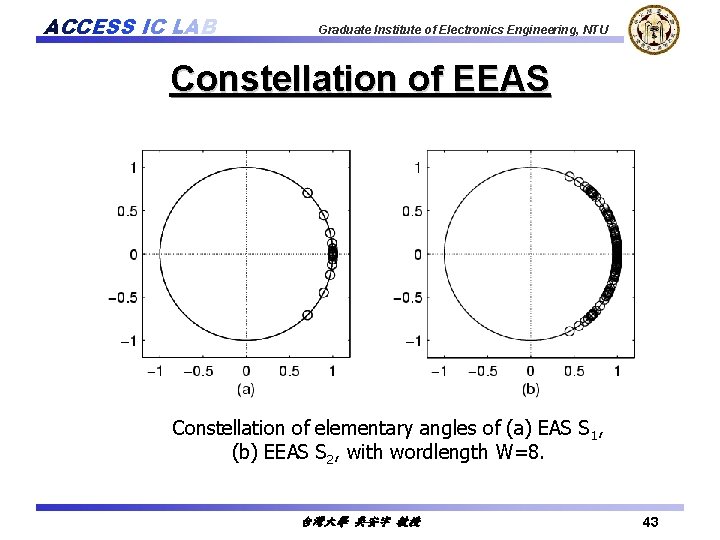
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Constellation of EEAS Constellation of elementary angles of (a) EAS S 1, (b) EEAS S 2, with wordlength W=8. 台灣大學 吳安宇 教授 43

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Summary of EEAS Scheme v Both micro-rotation and scaling phases 台灣大學 吳安宇 教授 44

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU VLSI Architecture v Iterative structure for one-stage rotational operation 台灣大學 吳安宇 教授 45

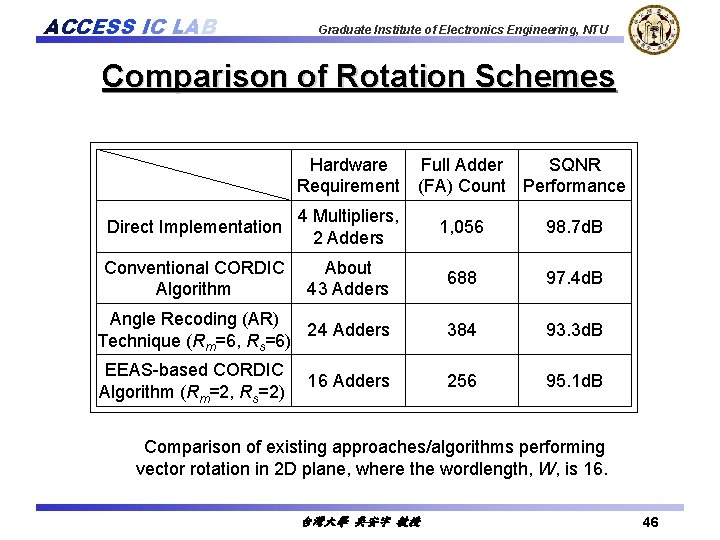
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Comparison of Rotation Schemes Hardware Full Adder SQNR Requirement (FA) Count Performance Direct Implementation 4 Multipliers, 2 Adders 1, 056 98. 7 d. B Conventional CORDIC Algorithm About 43 Adders 688 97. 4 d. B Angle Recoding (AR) 24 Adders Technique (Rm=6, Rs=6) 384 93. 3 d. B EEAS-based CORDIC Algorithm (Rm=2, Rs=2) 256 95. 1 d. B 16 Adders Comparison of existing approaches/algorithms performing vector rotation in 2 D plane, where the wordlength, W, is 16. 台灣大學 吳安宇 教授 46

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Outline v Introduction v Conventional CORDIC Algorithm v Enhancement of CORDIC v MVR-CORDIC Algorithm v EEAS-Based CORDIC Algorithm ü Vector Rotational CORDIC Family 台灣大學 吳安宇 教授 47

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Family of Vector Rotational CORDIC Algorithm 台灣大學 吳安宇 教授 48

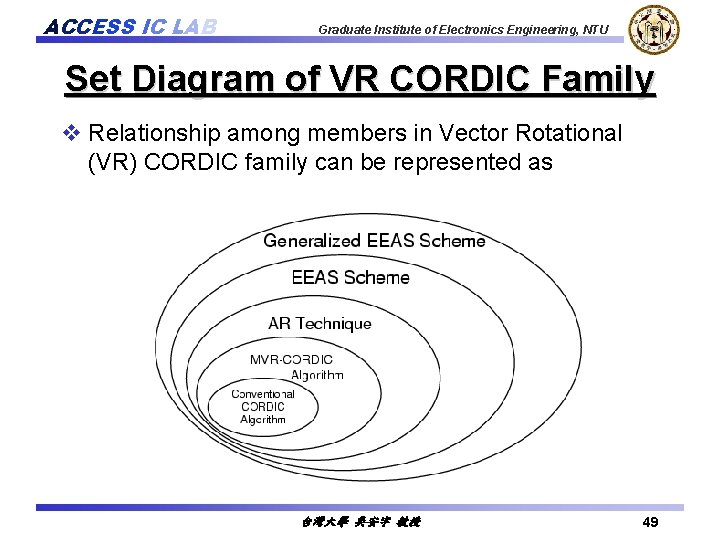
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Set Diagram of VR CORDIC Family v Relationship among members in Vector Rotational (VR) CORDIC family can be represented as 台灣大學 吳安宇 教授 49

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Angle Quantization v Approximation is applied on “ANGLE” v Decompose target angle into sub-angles 台灣大學 吳安宇 教授 50

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Angle Quantization (Cont. ) v Two key design issues in AQ process 1) Determine (construct) the sub-angle, and each sub-angle needs to be easy-to-implementation in practical implementation. 2) How to combine sub-angles such that angle quantization can be minimized. 台灣大學 吳安宇 教授 51

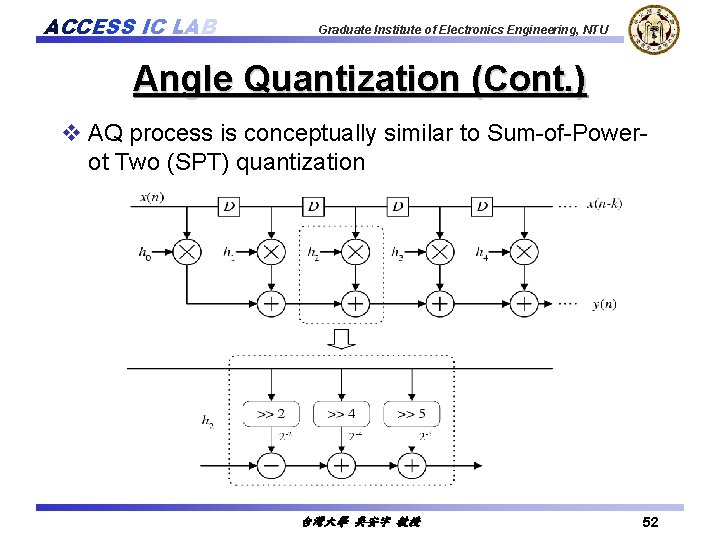
ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Angle Quantization (Cont. ) v AQ process is conceptually similar to Sum-of-Powerot Two (SPT) quantization 台灣大學 吳安宇 教授 52

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Angle Quantization (Cont. ) v Correspondences between AQ process and SPT (CSD) quantization process 台灣大學 吳安宇 教授 53

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Conclusion v Rotational Engine plays an important role in modern DSP systems v The conventional CORDIC is an interesting idea to reduce VLSI hardware cost in implementing the rotation operation (as well as other arithmetic operations). v The idea of Angle Quantization is firstly introduced in Ref. [4, 5]. It is analogous to the SPT concept in quantizing floating-point numbers. v Most CORDIC-related algorithms can be explained using the AQ design framework 台灣大學 吳安宇 教授 54

ACCESS IC LAB Graduate Institute of Electronics Engineering, NTU Reference 1. 2. 3. 4. 5. 6. Y. H. Hu, , “CORDIC-based VLSI architectures for digital signal processing”, IEEE Signal Processing Magazine , Vol. 9, Issue: 3, pp. 16 -35, July 1992. E. Antelo, J. Villalba, J. D. Bruguera, and E. L. Zapata, ” High performance rotation architectures based on the radix-4 CORDIC algorithm”, IEEE Transactions on Computers, Vol. 46, Issue: 8, Aug. 1997. C. S Wu and A. Y. Wu, “Modified vector rotational CORDIC (MVR-CORDIC) algorithm and architecture”, IEEE Trans. Circuits and systems-II: analog and digital signal processing, vol. 48, No. 6, June 2001. A. Y. Wu and C. S. Wu, “A unified design framework for vector rotational CORDIC family based on angle quantization process”, In Proc. of 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 2, pp. 1233 -1236. A. Y. Wu and Cheng-Shing Wu, “A Unified View for Vector Rotational CORDIC Algorithms and Architectures based on Angle Quantization Approach, ” in IEEE Trans. Circuits and Systems Part-I: Fundamental Theory and Applications, vol. 49, no. 10, pp. 1442 -1456, Oct. 2002. C. S. Wu and A. Y. Wu, “A novel trellis-based searching scheme for EEASbased CORDIC algorithm” In Proc. of 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 2 , pp. 1229 -1232. 台灣大學 吳安宇 教授 55