Gradients of Straight Lines and their Graphs What

Gradients of Straight Lines and their Graphs What is gradient or slope How to graph equations and find equations of graphs.

Contents • • • Gradient or Slope Examples: To find the gradient Sketch graphs using the table method Exercise: Sketch graphs Drawing straight lines using intercepts The gradient intercept form of a line Graph an equation in the form y = mx + c Find the equation of a straight line Examples: Find equations of lines

Gradient or Slope • Consider a hiker walking up a hill. • Gradient or slope is the steepness of the hill the hiker is walking up. • To find gradient we need to know the height climbed and the distance walked horizontally. Gradient = Height Distance Gradient of any line = vertical distance (height) horizontal distance

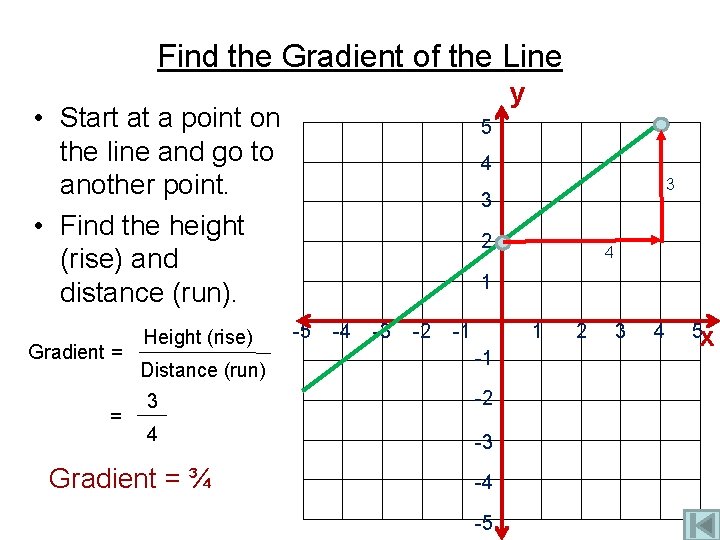
Find the Gradient of the Line y • Start at a point on the line and go to another point. • Find the height (rise) and distance (run). Gradient = = Height (rise) Distance (run) 5 4 3 2 4 1 -5 -4 -3 -2 -1 1 -1 3 -2 4 -3 Gradient = ¾ 3 -4 -5 2 3 4 5 x

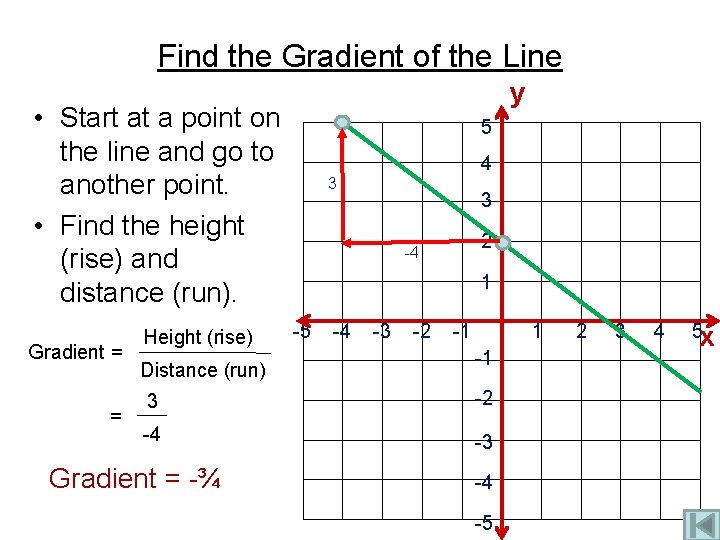
Find the Gradient of the Line y • Start at a point on the line and go to another point. • Find the height (rise) and distance (run). Gradient = = Height (rise) Distance (run) 5 4 3 3 2 -4 1 -5 -4 -3 -2 -1 1 -1 3 -2 -4 -3 Gradient = -¾ -4 -5 2 3 4 5 x

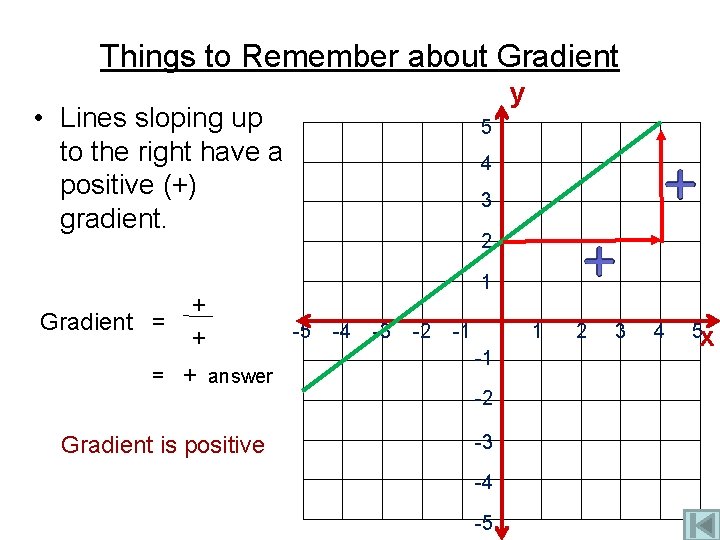
Things to Remember about Gradient y • Lines sloping up to the right have a positive (+) gradient. Gradient = = + + + answer Gradient is positive 5 4 3 2 1 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

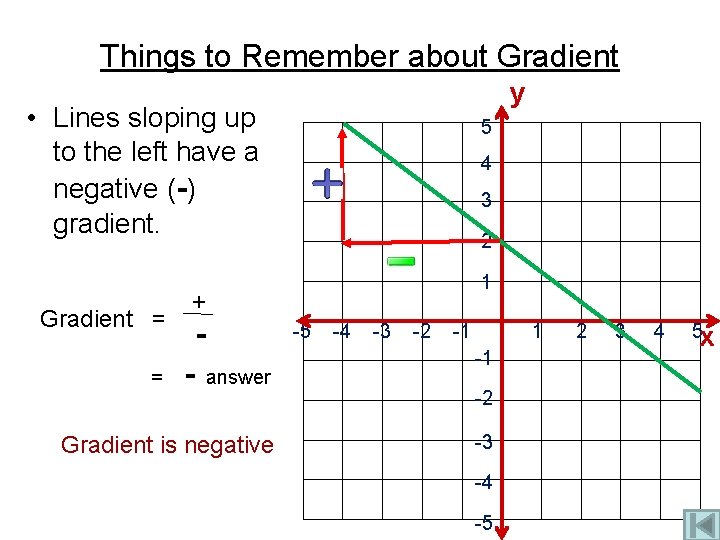
Things to Remember about Gradient y • Lines sloping up to the left have a negative (-) gradient. Gradient = = 5 4 3 2 1 + - answer Gradient is negative -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

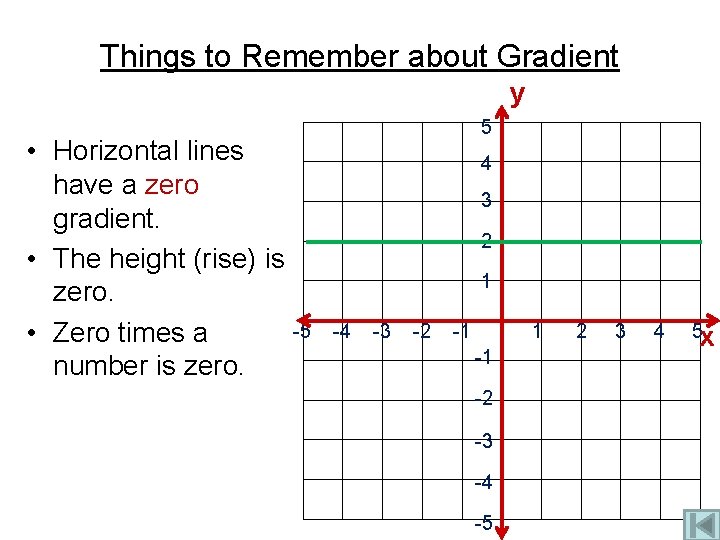
Things to Remember about Gradient y • Horizontal lines have a zero gradient. • The height (rise) is zero. • Zero times a number is zero. 5 4 3 2 1 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

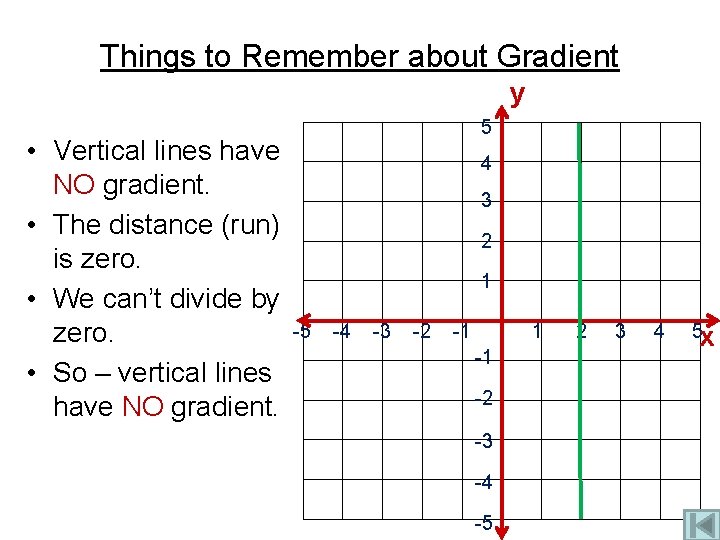
Things to Remember about Gradient y • Vertical lines have NO gradient. • The distance (run) is zero. • We can’t divide by zero. • So – vertical lines have NO gradient. 5 4 3 2 1 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

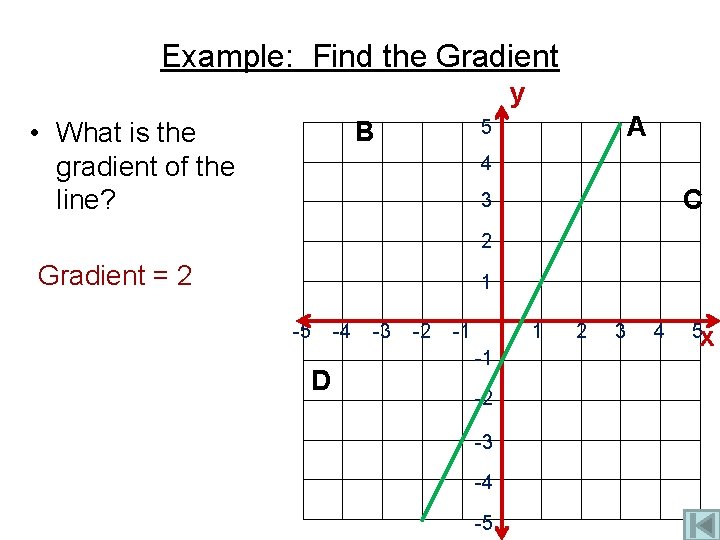
Example: Find the Gradient y A 5 B • What is the gradient of the line? 4 C 3 2 Gradient = 2 1 -5 D -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

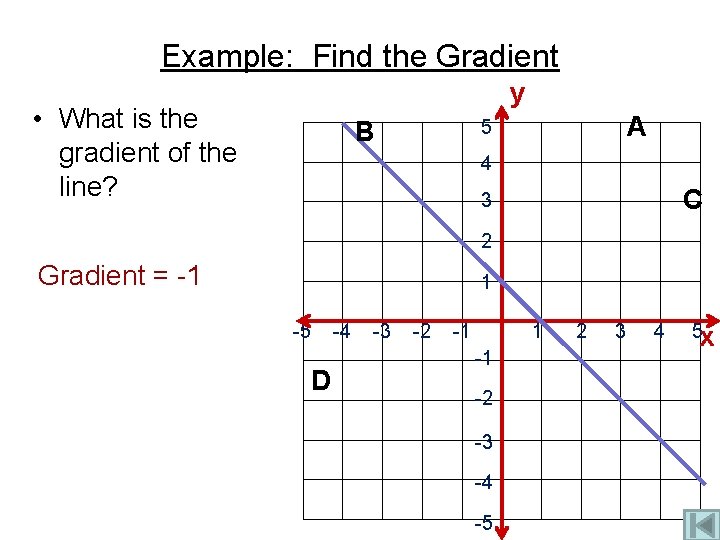
Example: Find the Gradient y • What is the gradient of the line? A 5 B 4 C 3 2 Gradient = -1 1 -5 D -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

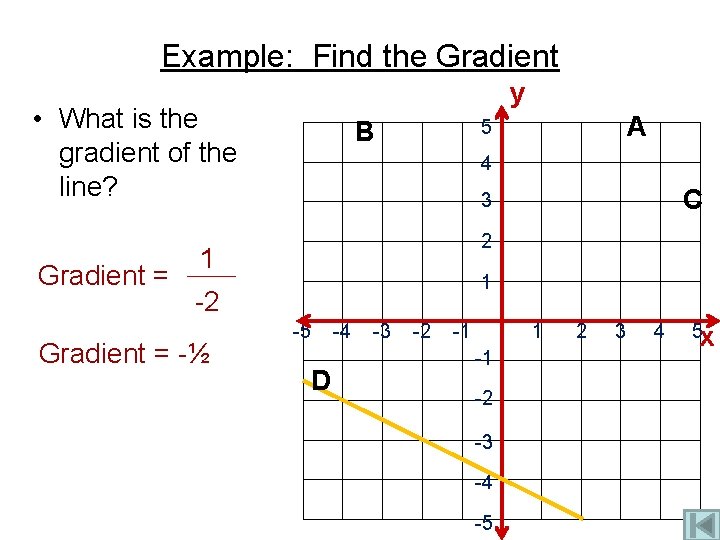
Example: Find the Gradient y • What is the gradient of the line? Gradient = 4 C 3 2 1 1 -2 Gradient = -½ A 5 B -5 D -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

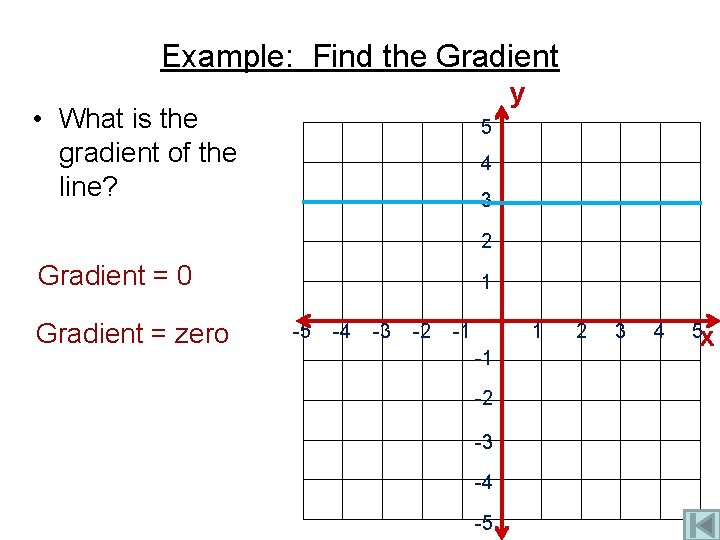
Example: Find the Gradient y • What is the gradient of the line? 5 4 3 2 Gradient = 0 Gradient = zero 1 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

Sketch Graphs using Table Method • You are given an equation to graph. – e. g. y = 2 x - 5 • You give x some values and work out the corresponding values for y. • Plot the points and draw the line through them – this is the graph of the equation. • Because you give x values, it is called the independent variable. • Y’s value depends on the value you gave to x. Y is therefore called the dependent variable.

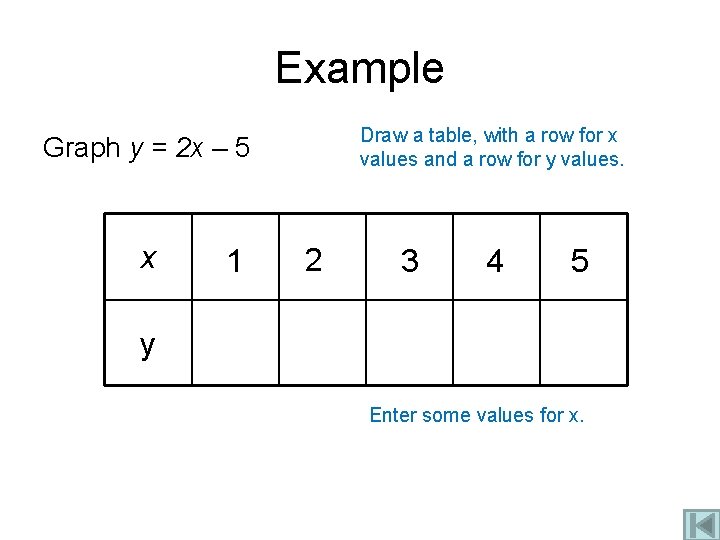
Example Draw a table, with a row for x values and a row for y values. Graph y = 2 x – 5 x 1 2 3 4 5 y Enter some values for x.

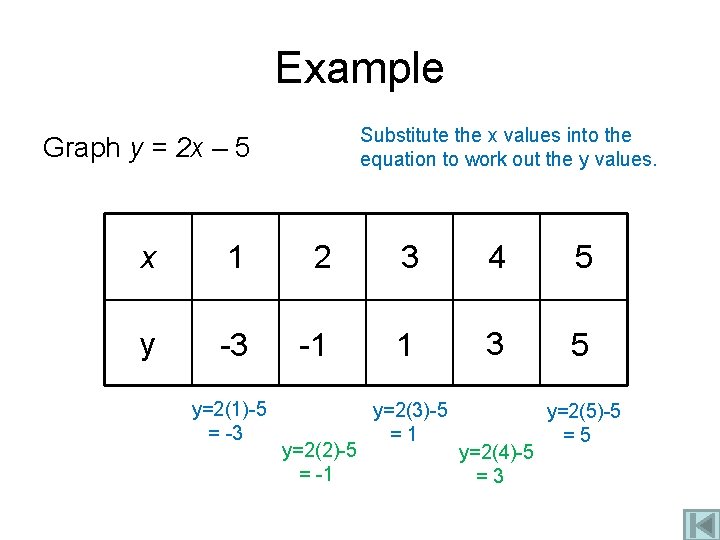
Example Substitute the x values into the equation to work out the y values. Graph y = 2 x – 5 x 1 2 3 4 5 y -3 -1 1 3 5 y=2(1)-5 = -3 y=2(2)-5 = -1 y=2(3)-5 =1 y=2(4)-5 =3 y=2(5)-5 =5

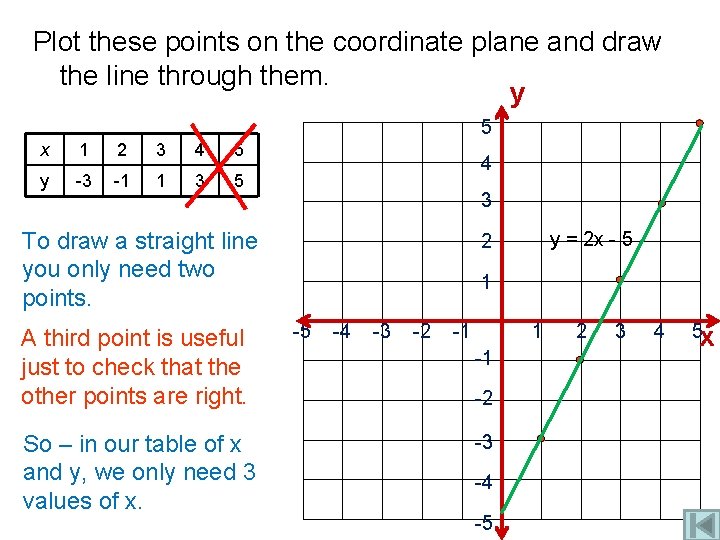
Plot these points on the coordinate plane and draw the line through them. y 5 x 1 2 3 4 5 y -3 -1 1 3 5 4 3 To draw a straight line you only need two points. A third point is useful just to check that the other points are right. So – in our table of x and y, we only need 3 values of x. y = 2 x - 5 2 1 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

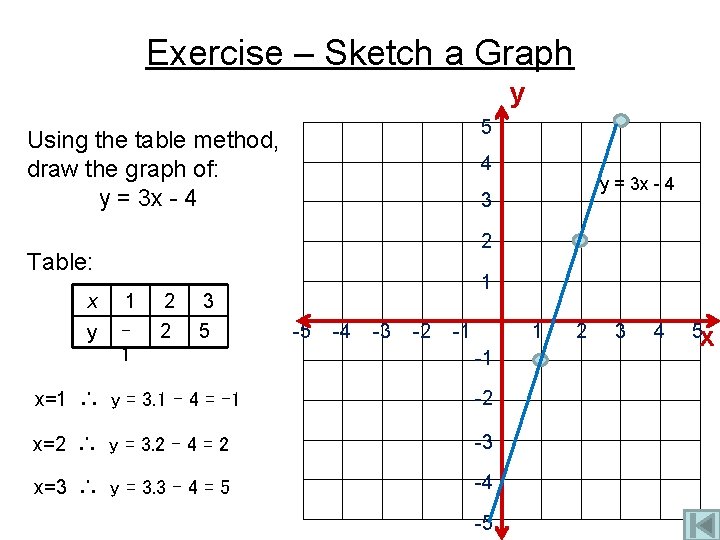
Exercise – Sketch a Graph y 5 Using the table method, draw the graph of: y = 3 x - 4 4 3 2 Table: x y y = 3 x - 4 1 1 2 3 2 5 1 -5 -4 -3 -2 -1 1 -1 x=1 ∴ y = 3. 1 – 4 = -1 -2 x=2 ∴ y = 3. 2 – 4 = 2 -3 x=3 ∴ y = 3. 3 – 4 = 5 -4 -5 2 3 4 5 x

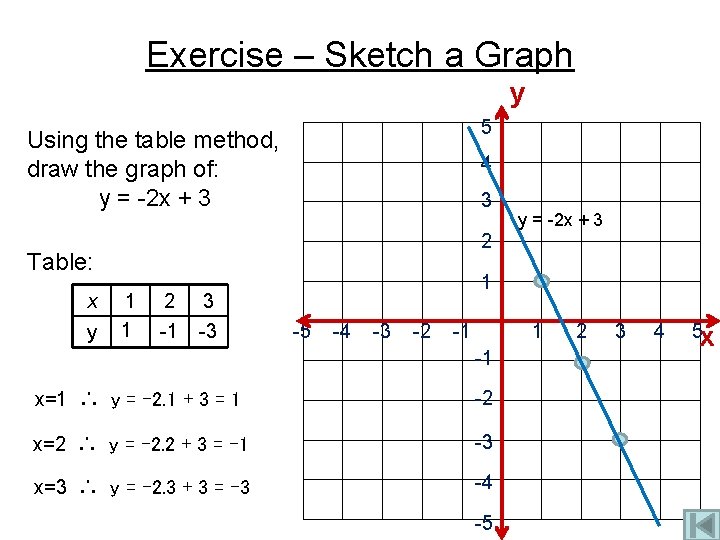
Exercise – Sketch a Graph y 5 Using the table method, draw the graph of: y = -2 x + 3 4 3 2 Table: x y y = -2 x + 3 1 1 2 3 -1 -3 1 -5 -4 -3 -2 -1 1 -1 x=1 ∴ y = -2. 1 + 3 = 1 -2 x=2 ∴ y = -2. 2 + 3 = -1 -3 x=3 ∴ y = -2. 3 + 3 = -3 -4 -5 2 3 4 5 x

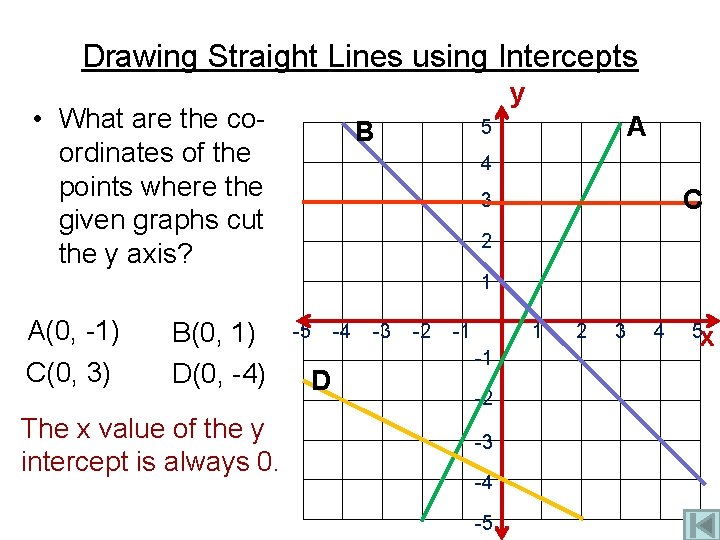
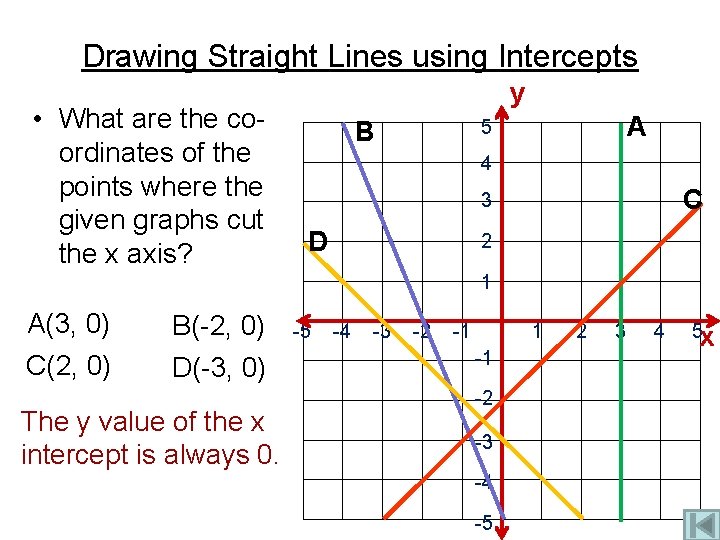
Drawing Straight Lines using Intercepts y • What are the coordinates of the points where the given graphs cut the y axis? A 5 B 4 C 3 2 1 A(0, -1) C(0, 3) B(0, 1) D(0, -4) The x value of the y intercept is always 0. -5 D -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

Drawing Straight Lines using Intercepts • What are the coordinates of the points where the given graphs cut the x axis? y A 5 B 4 C 3 D 2 1 A(3, 0) C(2, 0) B(-2, 0) D(-3, 0) The y value of the x intercept is always 0. -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 2 3 4 5 x

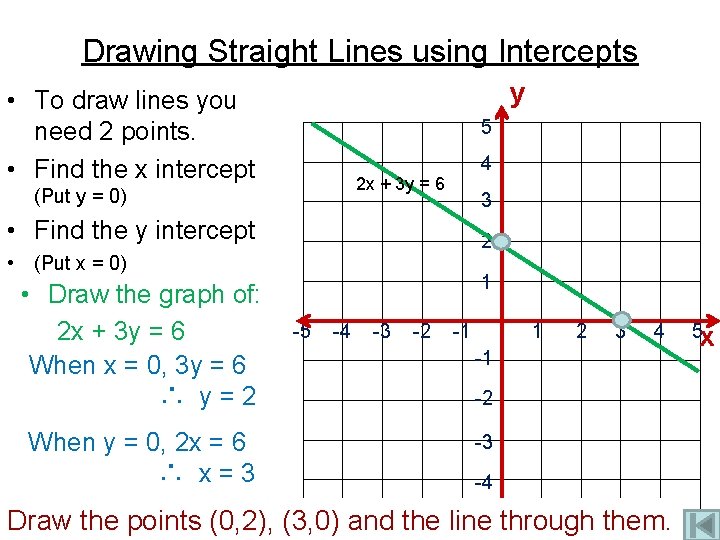
Drawing Straight Lines using Intercepts y • To draw lines you need 2 points. • Find the x intercept 5 4 2 x + 3 y = 6 (Put y = 0) 3 • Find the y intercept 2 • (Put x = 0) • Draw the graph of: 2 x + 3 y = 6 When x = 0, 3 y = 6 ∴ y=2 When y = 0, 2 x = 6 ∴ x=3 1 -5 -4 -3 -2 -1 1 2 3 4 -1 -2 -3 -4 Draw the points (0, 2), (3, 0) and the line -5 through them. 5 x

The Gradient-Intercept Form of a Straight Line • When a linear function is written in the form y = mx + b • then m is the gradient and the b the y-intercept. For the equation: y = 3 x + 5 The y intercept is ? 5 The gradient is ? 3 For the equation: y = ¾x + 1 The y intercept is ? 1 The gradient is ? ¾

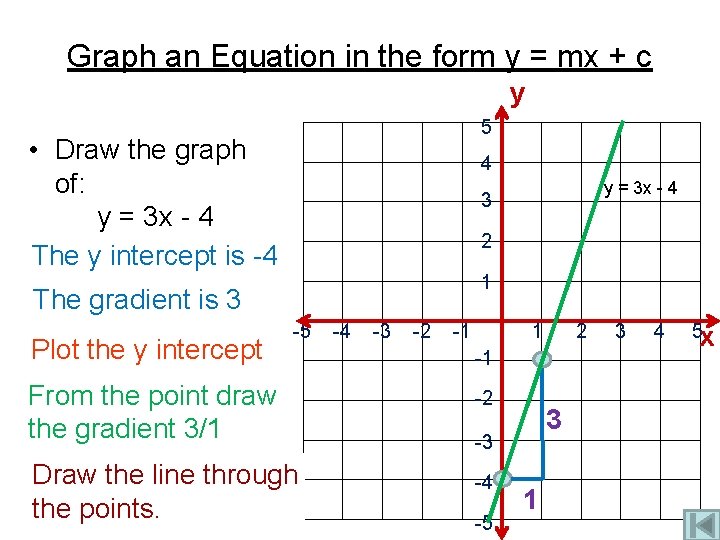
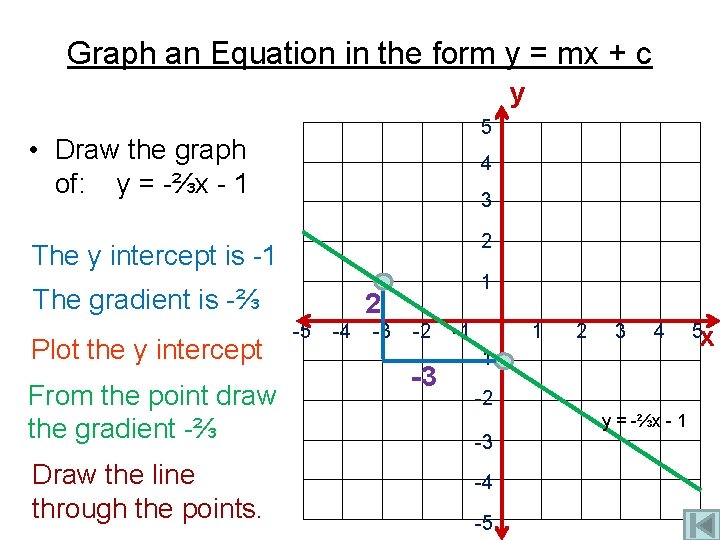
Graph an Equation in the form y = mx + c y 5 • Draw the graph of: y = 3 x - 4 The y intercept is -4 4 2 1 The gradient is 3 Plot the y intercept y = 3 x - 4 3 -5 From the point draw the gradient 3/1 Draw the line through the points. -4 -3 -2 -1 1 2 -1 -2 3 -3 -4 -5 1 3 4 5 x

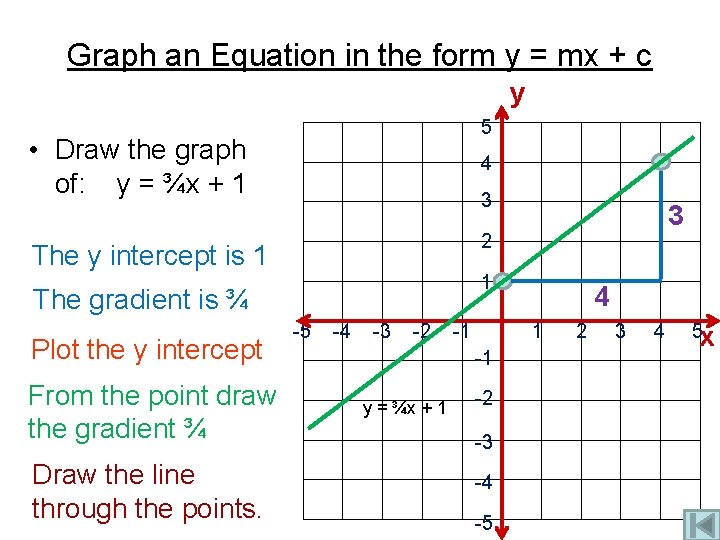
Graph an Equation in the form y = mx + c y 5 • Draw the graph of: y = ¾x + 1 4 3 2 The y intercept is 1 1 The gradient is ¾ Plot the y intercept From the point draw the gradient ¾ Draw the line through the points. 3 -5 -4 -3 -2 -1 1 -1 y = ¾x + 1 4 -2 -3 -4 -5 2 3 4 5 x

Graph an Equation in the form y = mx + c y 5 • Draw the graph of: y = -⅔x - 1 4 3 2 The y intercept is -1 The gradient is -⅔ Plot the y intercept From the point draw the gradient -⅔ Draw the line through the points. 1 2 -5 -4 -3 -2 -3 -1 1 2 3 4 -1 -2 -3 -4 -5 y = -⅔x - 1 5 x

Find the Equation of a Straight Line • To find the equation of a line, you need to know the gradient (m) and the y intercept (c). • Substitute these into the equation: y = mx + c 4 The y intercept is -1. The gradient is 1. c = -1 2 1 1 m=1 The equation of AB is: B 3 -4 -3 -2 -1 1 -1 -2 y=x-1 -3 A 1 -4 2 3 4

Find the Equation of a Straight Line • To find the equation of a line, you need to know the gradient (m) and the y intercept (c). • Substitute these into the equation: y = mx + c A 4 The y intercept is 2. 3 2 c=2 -3 1 The gradient is -⅔. m = -⅔ The equation of AB is: y = -⅔ x + 2 2 -4 -3 -2 -1 1 -1 -2 -3 -4 2 3 4 B

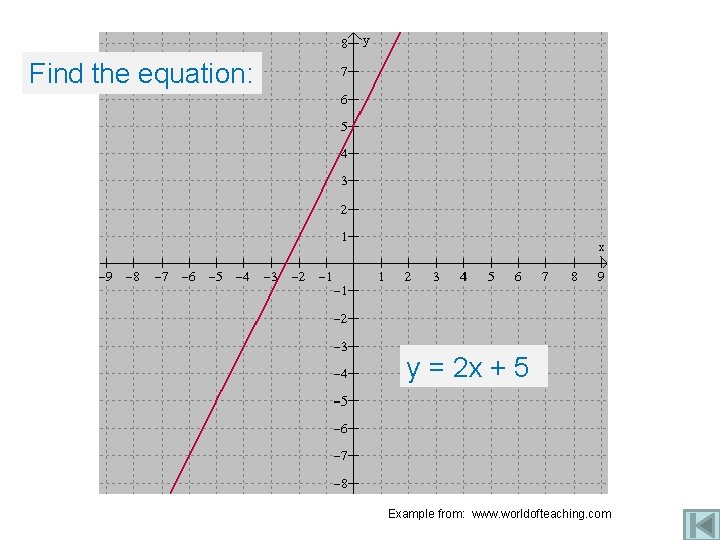
Find the equation: y = 2 x + 5 Example from: www. worldofteaching. com

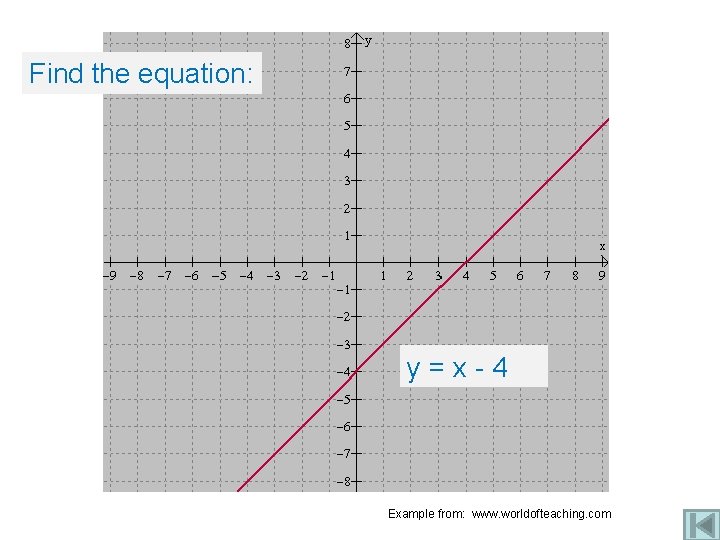
Find the equation: y=x-4 Example from: www. worldofteaching. com

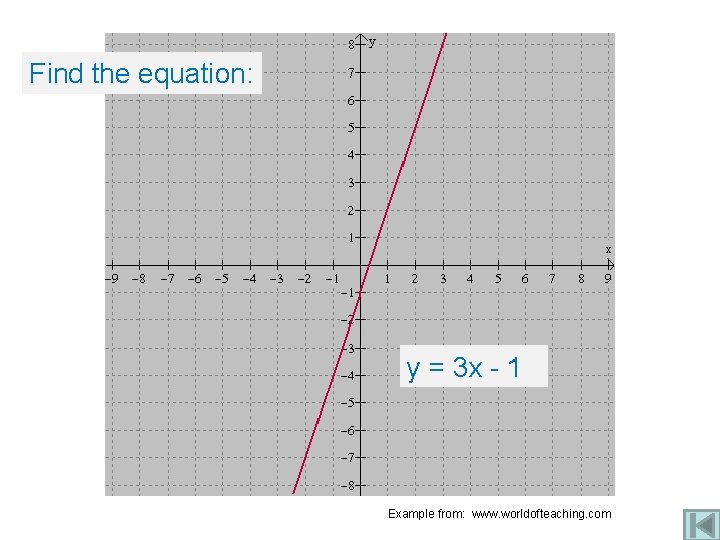
Find the equation: y = 3 x - 1 Example from: www. worldofteaching. com

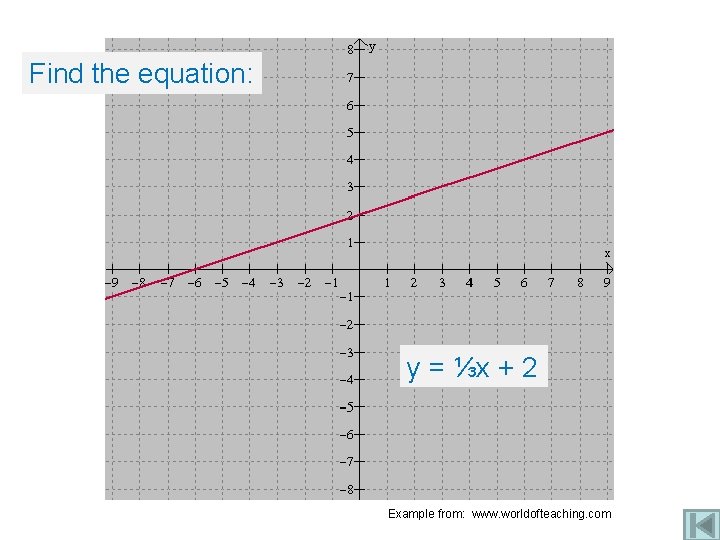
Find the equation: y = ⅓x + 2 Example from: www. worldofteaching. com

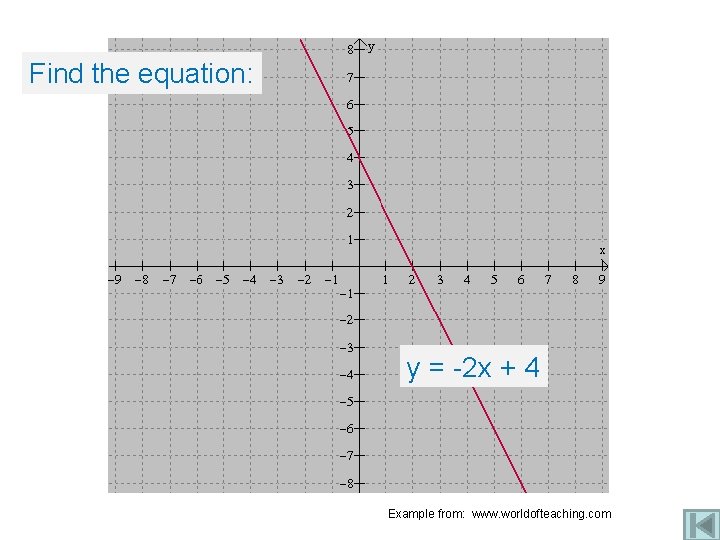
Find the equation: y = -2 x + 4 Example from: www. worldofteaching. com