Gradient based technique for electromagnetic layered earth model

Gradient based technique for electromagnetic layered earth model data inversion Claudio Patriarca, Andrea Di Matteo and Evert Slob 2011 IEEE Internation Geoscience and Remote Sensing Symposium, Vancouver BC, July 2011 Challenge the future 1

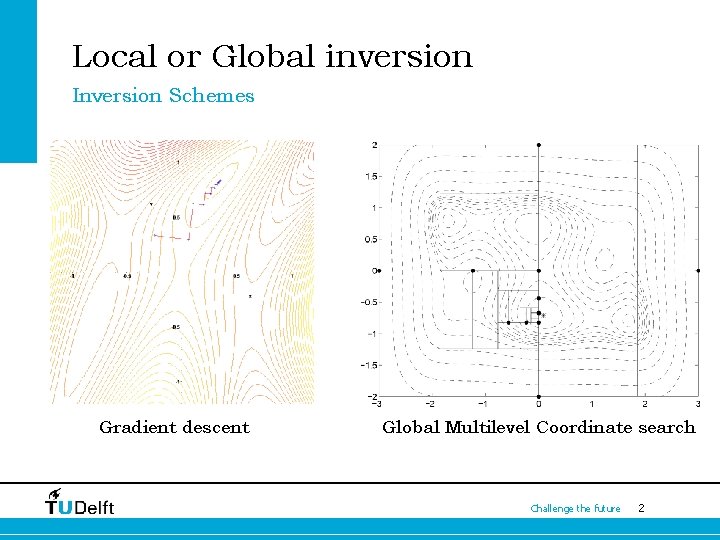
Local or Global inversion Inversion Schemes Gradient descent Global Multilevel Coordinate search Challenge the future 2

Full-waveform inversion EM Inversion Schemes – non linear • Size of parameter space – nr. layers • Number of local minima - nonlinearity • Parameter correlations – limit sensitivity • UWB – many frequency points Challenge the future 3

Towards local inversion Jacobian calculation Objective Function † Jacobian Challenge the future 4

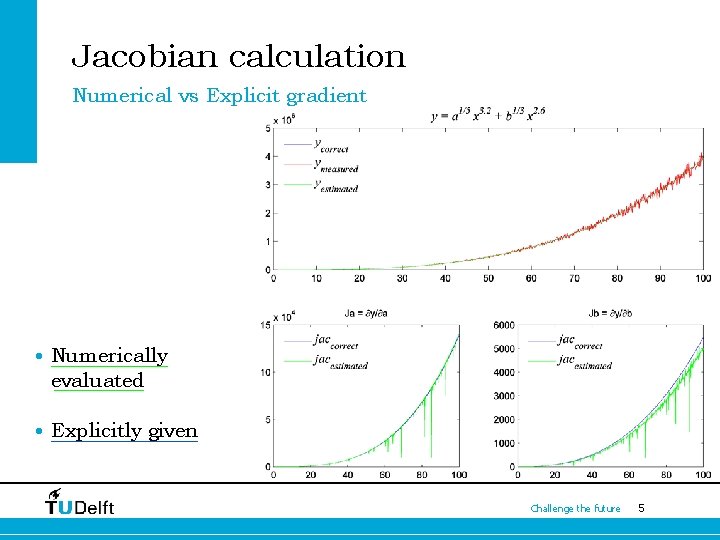
Jacobian calculation Numerical vs Explicit gradient • Numerically evaluated • Explicitly given Challenge the future 5

Local Full-waveform inversion Numerical test case #1: smooth model Challenge the future 6

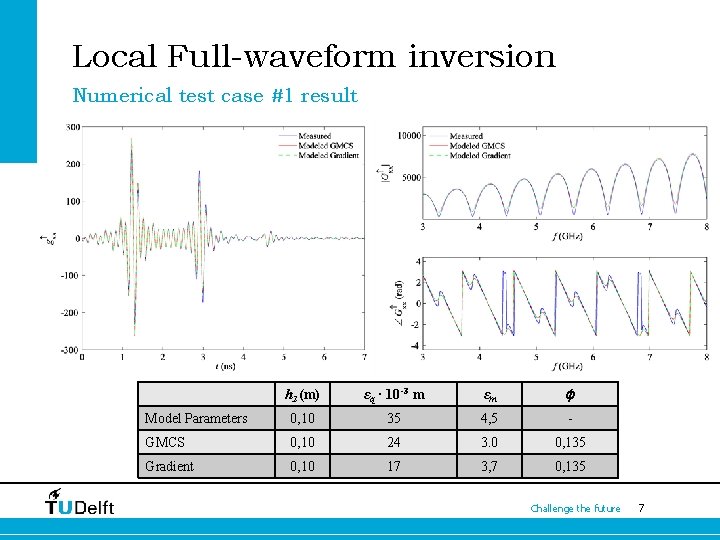
Local Full-waveform inversion Numerical test case #1 result h 2 (m) εq · 10 -3 m εm ϕ Model Parameters 0, 10 35 4, 5 - GMCS 0, 10 24 3. 0 0, 135 Gradient 0, 10 17 3, 7 0, 135 Challenge the future 7

Full-waveform inversion Real data test case • Large datasets • UWB data (SFCW) Marble floor element in the Ancient theatre of Megalopolis, Greece Challenge the future 8

Local Full-waveform inversion Real data test case Challenge the future 9

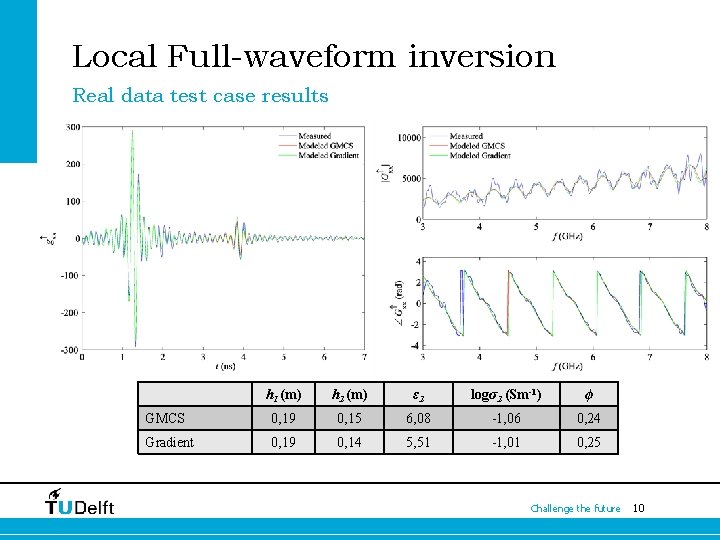
Local Full-waveform inversion Real data test case results h 1 (m) h 2 (m) ε 2 logσ2 (Sm-1) ϕ GMCS 0, 19 0, 15 6, 08 -1, 06 0, 24 Gradient 0, 19 0, 14 5, 51 -1, 01 0, 25 Challenge the future 10

Local Full-waveform inversion Numerical test case #2: piecewise layered half-space Challenge the future 11

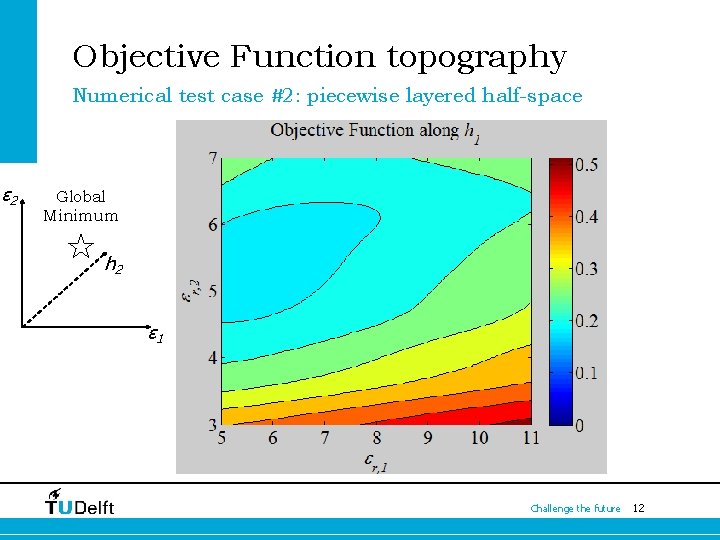
Objective Function topography Numerical test case #2: piecewise layered half-space ε 2 Global Minimum h 2 ε 1 Challenge the future 12

Conclusion • Local inversion advantages in moving downhill; problems with local minima • Comparison Global and Local search numerical and real data: success of local methods in specialized applications • Use explicit gradient • Deep interfaces? • Convenient implementing Hessian? Challenge the future 13