Grade A Cubic and Reciprocal Functions Recognise sketch

Grade A* Cubic and Reciprocal Functions Recognise, sketch and interpret graphs of simple cubic functions and reciprocal functions y = 1/x where x is not 0 If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Key Vocabulary Cubic Reciprocal Function Graph Asymptote Turning point Origin Symmetrical

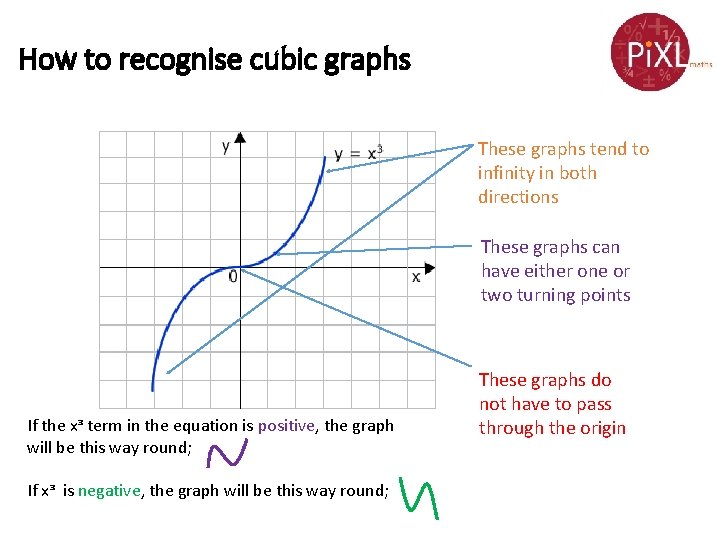
How to recognise cubic graphs These graphs tend to infinity in both directions These graphs can have either one or two turning points If the xᵌ term in the equation is positive, the graph will be this way round; If xᵌ is negative, the graph will be this way round; These graphs do not have to pass through the origin

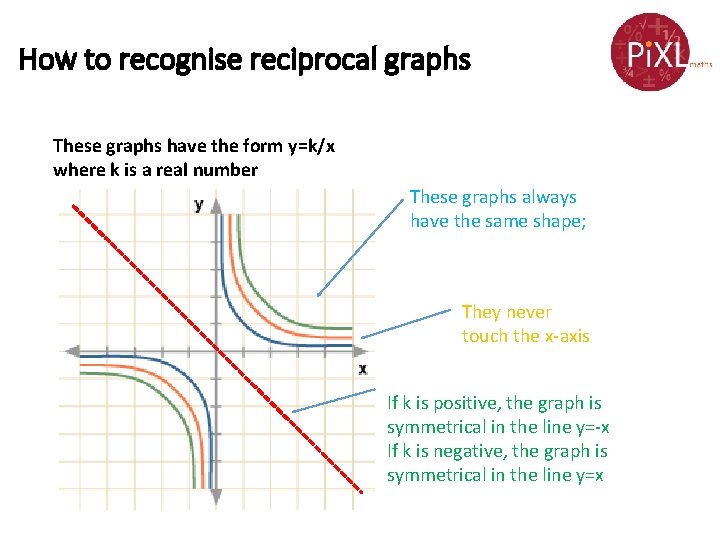
How to recognise reciprocal graphs These graphs have the form y=k/x where k is a real number These graphs always have the same shape; They never touch the x-axis If k is positive, the graph is symmetrical in the line y=-x If k is negative, the graph is symmetrical in the line y=x

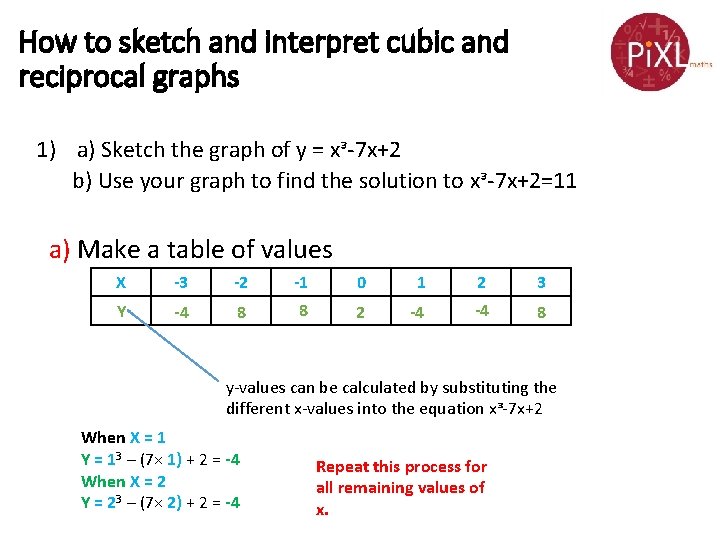
How to sketch and interpret cubic and reciprocal graphs 1) a) Sketch the graph of y = xᵌ-7 x+2 b) Use your graph to find the solution to xᵌ-7 x+2=11 a) Make a table of values X -3 -2 -1 0 1 2 3 Y -4 8 8 2 -4 -4 8 y-values can be calculated by substituting the different x-values into the equation xᵌ-7 x+2 When X = 1 Y = 13 – (7× 1) + 2 = -4 When X = 2 Y = 23 – (7× 2) + 2 = -4 Repeat this process for all remaining values of x.

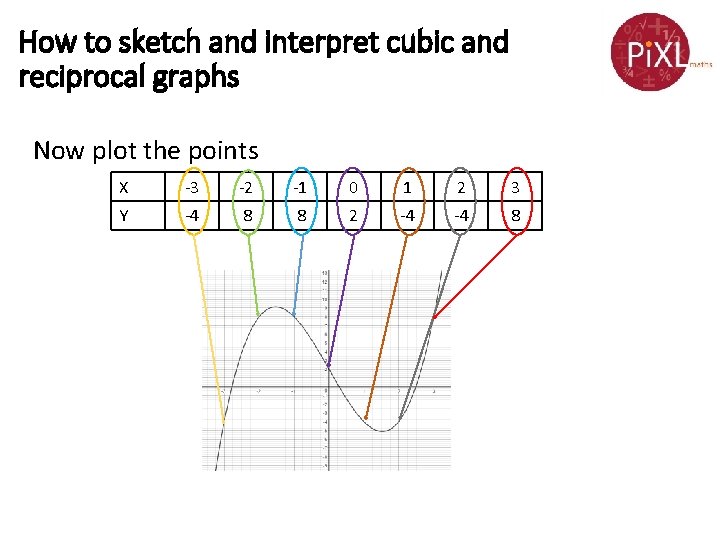
How to sketch and interpret cubic and reciprocal graphs Now plot the points X -3 -2 -1 0 1 2 3 Y -4 8 8 2 -4 -4 8

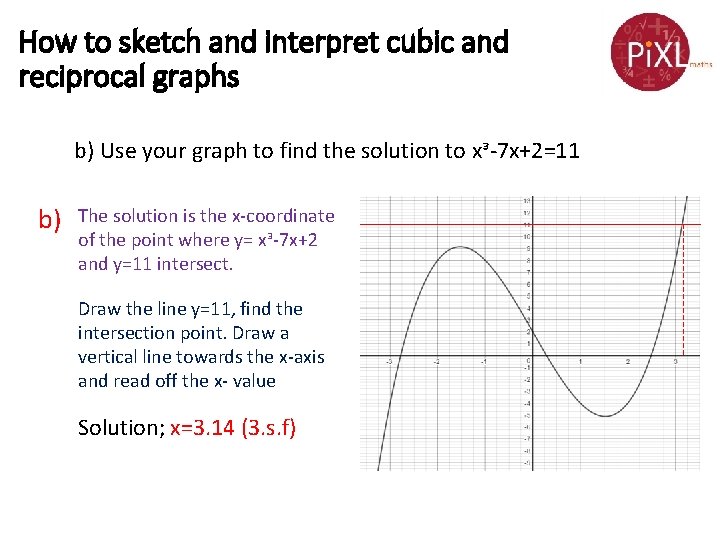
How to sketch and interpret cubic and reciprocal graphs b) Use your graph to find the solution to xᵌ-7 x+2=11 b) The solution is the x-coordinate of the point where y= xᵌ-7 x+2 and y=11 intersect. Draw the line y=11, find the intersection point. Draw a vertical line towards the x-axis and read off the x- value Solution; x=3. 14 (3. s. f)

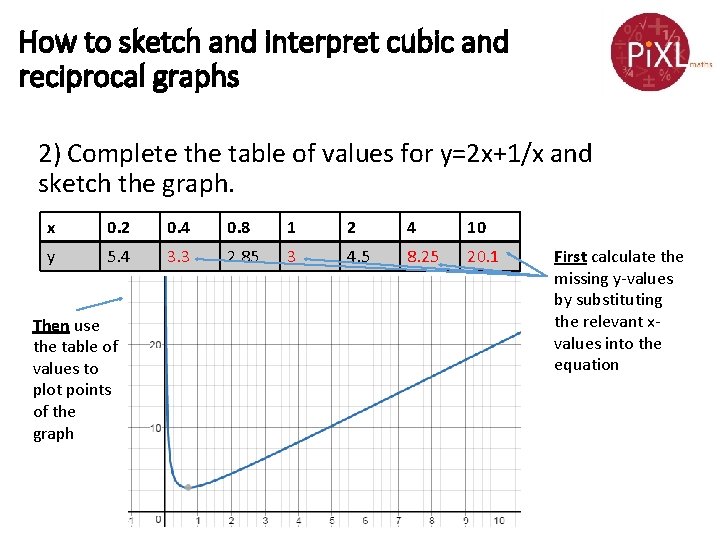
How to sketch and interpret cubic and reciprocal graphs 2) Complete the table of values for y=2 x+1/x and sketch the graph. x 0. 2 0. 4 0. 8 1 2 4 10 y 5. 4 3. 3 2. 85 3 4. 5 8. 25 20. 1 Then use the table of values to plot points of the graph First calculate the missing y-values by substituting the relevant xvalues into the equation

Solve the following problems – now you try… 1. Sketch the following cubic graphs a) y=-x³ b) y=3 -x³ c) y=x³-4 x²+5 x 2. Sketch the following reciprocal graphs a) y=4/x b) y=5+5/x c) y=3 x-2/x

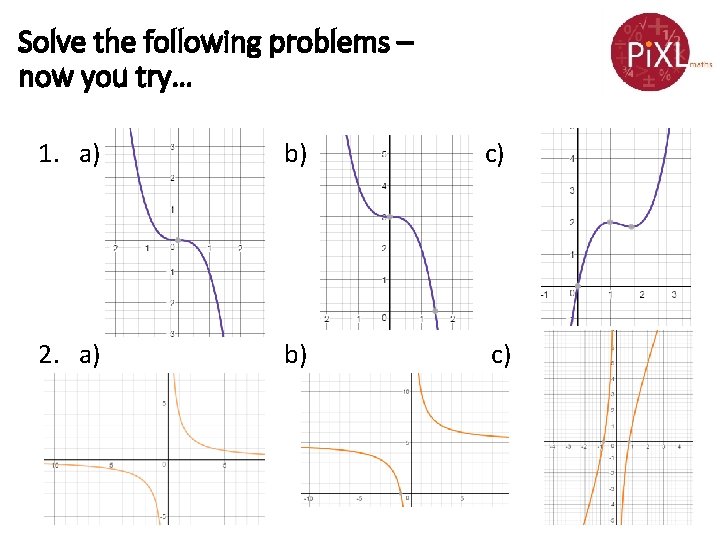
Solve the following problems – now you try… 1. a) b) c) 2. a) b) c)

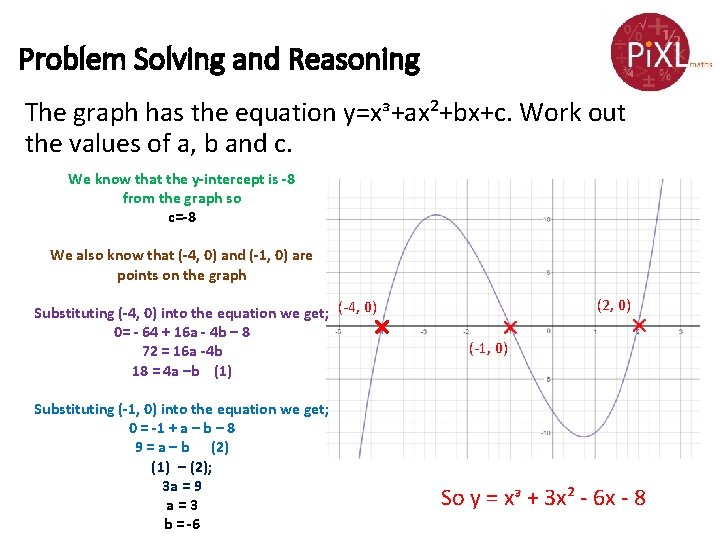
Problem Solving and Reasoning The graph has the equation y=xᵌ+ax²+bx+c. Work out the values of a, b and c. We know that the y-intercept is -8 from the graph so c=-8 We also know that (-4, 0) and (-1, 0) are points on the graph Substituting (-4, 0) into the equation we get; (-4, 0) 0= - 64 + 16 a - 4 b – 8 72 = 16 a -4 b 18 = 4 a –b (1) Substituting (-1, 0) into the equation we get; 0 = -1 + a – b – 8 9 = a – b (2) (1) – (2); 3 a = 9 a=3 b = -6 (2, 0) (-1, 0) So y = xᵌ + 3 x² - 6 x - 8

Reason and explain • Will the graph of y = -45/x have a line of symmetry of y = -x? • How many solutions are there for the equation 4+5 x 2 -2 x 3 - x=5? • Let y = k/x. Describe the change in the graph as k tends to infinity from 1.