Grade 9 Math Powers Exponents What does the









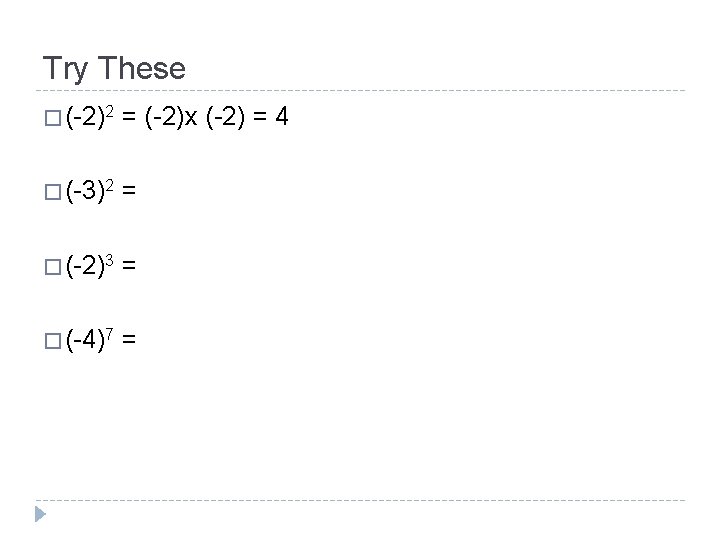
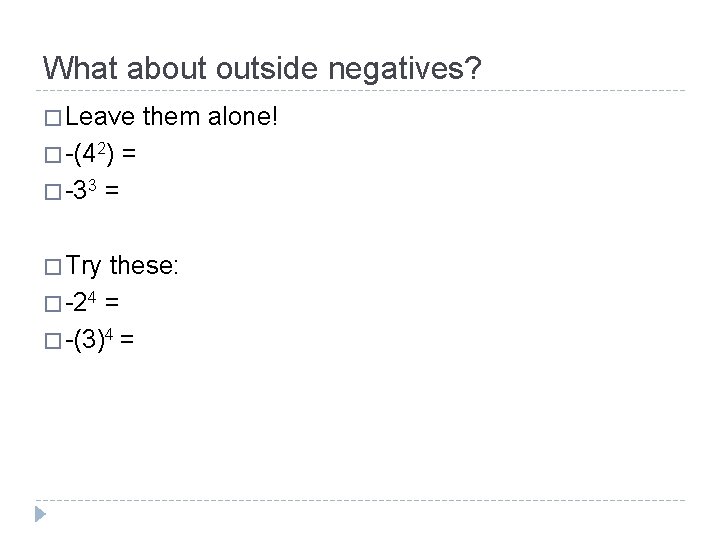




















- Slides: 35

Grade 9 Math Powers & Exponents

What does the E stand for in BEDMAS? � Brackets �E � Division � Multiplication � Addition � Subtraction � An In either order exponent is a symbol or number placed above and after another symbol or number to denote the power to which the latter is to be raised; in x 4, 4 is the exponent

Repeated Multiplication � Remember � It when you first learned to multiply 2 * 5 meant that you added 2 to itself five times � An Exponent just means to multiply a number by itself � So 24 means you multiply 2 by itself four times � Write out 23 and 32 as repeated multiplication. Are they the same?

Question �A type of bacteria reproduces every hour and always produces the same number of offspring. In the fifth hour, 1024 offspring are produced. How many offspring does each bacterium produce?

Definitions �A is the product obtained by multiplying a quantity by itself one or more times; the 3 rd power of 2 is 8 �A is the number which is multiplied by itself in a power � An is the number of times the base is multiplied by itself �A is one of two or more number that when multiplied together produce a given product; a divisor; Y X 2 3

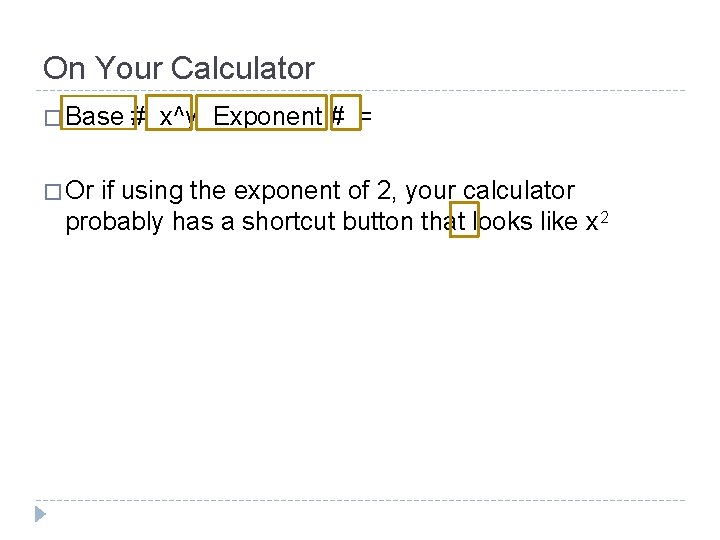
On Your Calculator � Base � Or # x^y Exponent # = if using the exponent of 2, your calculator probably has a shortcut button that looks like x 2

The Invisible Exponent � If you can’t see an exponent, it is a � A is really � Anything to the power of 1 is just itself because you only multiply it the once � So 31 = 3. � Your turn: � What is 1 0001

Zero as an Exponent � Anything to the power of 0 is � A 0 =1 � 30 = 1 � Why? � 33 = � 32 = � 31 = � 30 = Look for the pattern. .

Your Turn � W 0 = � 140 = � 990 = � P 1 = � 81 = � 741 =

What about Negatives? � Just remember to multiply your negatives the right number of times � Negative x Negative = � Negative x Negative = � (Negative)2 = � (Negative)3 = � (Negative)4 = � (Negative)7 = � (Negative)22 =
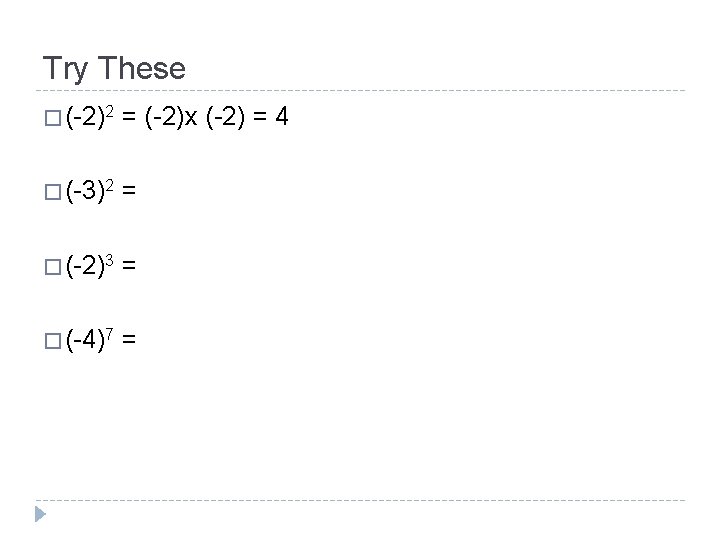
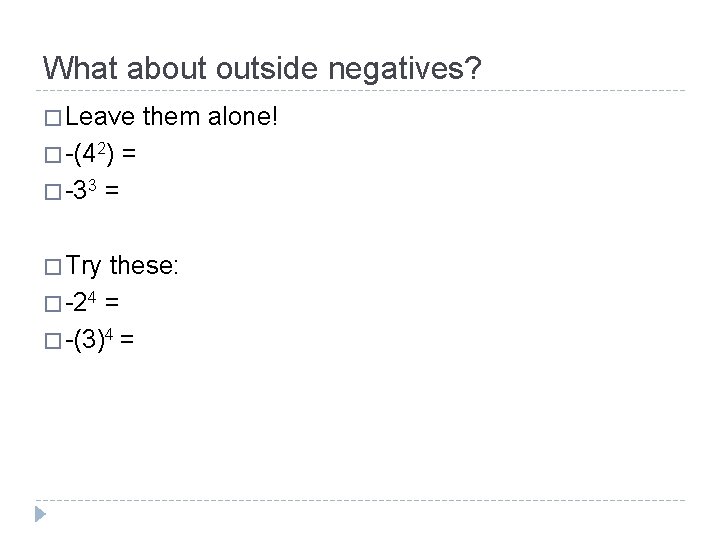
What about outside negatives? � Leave � -(42) � -33 � Try them alone! = = these: � -24 = � -(3)4 =

And Fractions. . . ? � How do you multiply fractions? �½ x ½ = 1 x 1 = � 2 2 � Same thing with exponents, take the top to the exponent and take the bottom to the exponent. � (3/4)2 = � Your turn: � (2/5)3

If it’s not the whole fraction. . . � Just take the right part to the exponent � 24 =2 x 2 x 2 x 2= � 5 5 � Try � 4 = � 33 this:

Put It All Together �F 0 �-(7/4)2 = � 141 = �-3 = � 42 �-990 = � 52 �(-P)1 = �(8/3)2 = = � 33 �(-7)2 � -34 = =

Product Law � When you multiply powers with the same base: � The base remains the same � Add the exponents � A 2 x A 3 = A 2+3 = A 5 � Why?

Quotient Law � If you add exponents when you multiply, it makes sense that you subtract exponents when you divide. � Keep the bases the same. � A 4 / A 3 = A 4 -3 = A 1 � Why?

Your turn � A 4 x A 2 � B 2 x B 5 � C 8 x C 6 � D 6/D 3 � E 36/E 9 � F 9/F 3 x F 7

Quotient Rule Proof that A 0 = 1

Reciprocal Law � If you have a negative exponent on the top, move the entire power to the bottom and it becomes positive. � If you have a negative exponent on the bottom, move the power to the top and it becomes positive. � REMEMBER: there is always an invisible one to leave behind � x(-3) � 1 2(-4)


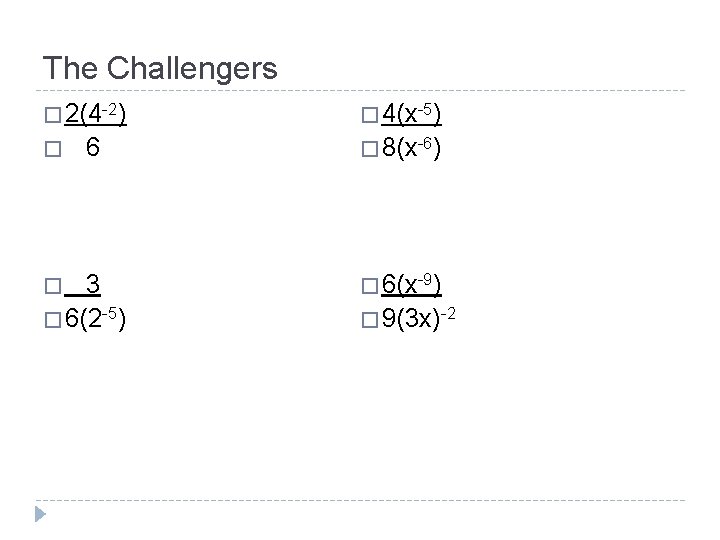
The Challengers � 2(4 -2) � 6 3 � 6(2 -5) � � 4(x-5) � 8(x-6) � 6(x-9) � 9(3 x)-2

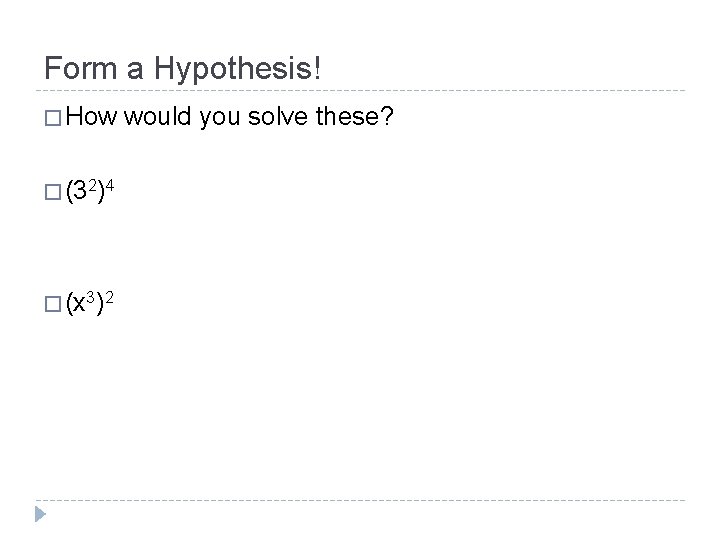
Form a Hypothesis! � How � (32)4 � (x 3)2 would you solve these?

(xa)b = xa*b � So (32)3 = � Or you could use BEDMAS: � (32)3 = � Try These � (x 3)2 = � (53)2 = � (48)1/2 =

Definitions �A root does the opposite of an exponent � A square root is the opposite of squaring. � When you only see the root sign and no number, it is a square root � √ = 2√ � On your calculator, type in the number you wish to take the square root of and then the square root button

On your calculator � For higher roots, find the button x√ � Type in the root you want first (if you want the third root, type in 3, fourth root, type in four, . . . ) � Then press the x√ button � Now, type in the number you are taking the root of � Ex. For the 3 rd root of 27, type in 3 x√ 27 and hit enter. � You should get as an answer.

Perfect Squares � Numbers that are equal to another number multiplied by itself � 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 169, . . .

Don’t forget the Negatives � So if a square root of a 36 is one that can be multiplied by itself to get 36, what number is the square root of 36? � Whenever you take an will have two answers � Whenever you take an will only have one answer root (2, 4, 6, 8, . . . ), you root (3, 5, 7, 9, . . . ), you


Fractional Exponents � If you have the √x 2, how do you simplify? � There � is another exponent law that says n√x = x 1/n � So √x 2 = x 2/2 = x 1 = x

Try These � √x 8 � √x 90 � ∛x 18 � ∛x 102 � ∜x 24

Root the Number, Divide the Exponent � √ 9 x 6 � √ ¼ x 10 � ∛ 27 x 27 � ∛ 64 x 102 � ∜ 625 x 24

Approximating Roots W/O Calculator � If √ 36 = 6 or -6 and √ 49 = 7 or -7, what does √ 40 =?

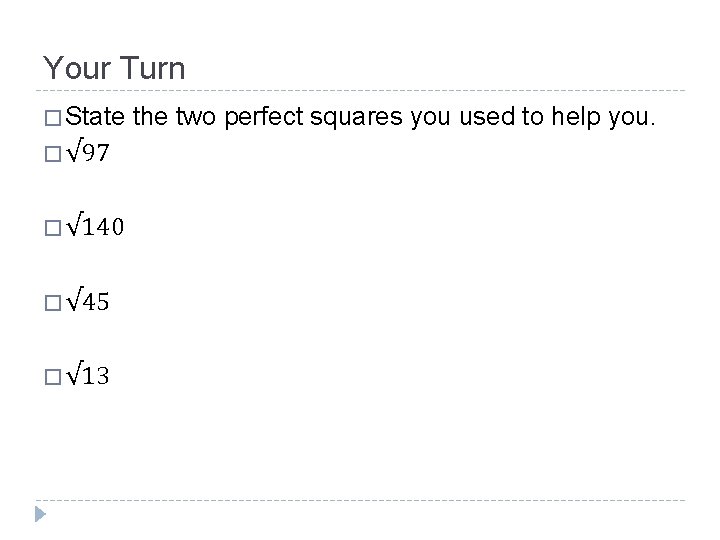
Your Turn � State � √ 97 � √ 140 � √ 45 � √ 13 the two perfect squares you used to help you.

Math Etiquette � Place � No variables in alphabetical order negative exponents in final answers � No roots in the denominator