GRADE 9 GRAPHS 1 THE STRAIGHT LINE GRAPH

GRADE 9 GRAPHS • 1. THE STRAIGHT LINE GRAPH: Std form: y = mx + c gradient y-intercept How to Draw a Straight Line Graph: Intercept-Intercept Method (Used if there is an x-term, a y-term and a number) Gradient-Intercept method (Used when the graph passes through (0; 0)) i. e when x = 0, y = 0). Special Lines: y=c x=k y=x y = -x 1

Intercept-Intercept Method (Used if there is an x-term, a y-term and a number) Step 1: y-int Let x = 0 Step 2: x-int Let y = 0 Step 3: Join the 2 intercepts. NOTE: Equation does not have to be in std form. Always show the x and y intercepts. Eg: On the same axes, draw rough graphs of: 2 x + 4 y = 8 and 2 x – y = 3 2 x + 4 y = 8: y-int: if x = 0, x-int: if y = 0 0 + 4 y = 8 4 y = _8 __ 4 4 y 2 x + 4 y = 8. . . y = 2 2 x – y = 3 2 1½ 4 x -3 2 x + 0 = 8. . . 2 x = 8 2 2. . . x = 4 2 x – y = 3 y-int: if x = 0, 0 -y=3 . . . y = -3 x-int: if y = 0 2 x - 0 = 3 . . . x = 3/2 2

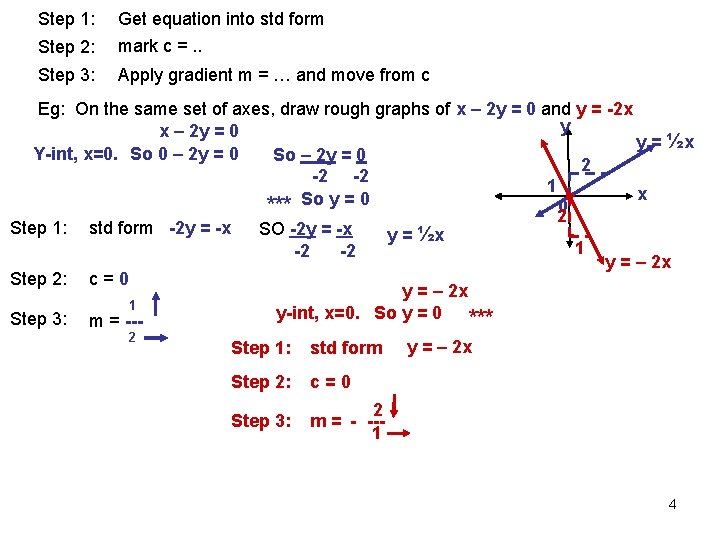
Gradient-Intercept Method: Use this when the graph passes through (0; 0) – will have an x-term, y-term and no other number other than 0. NOTE: - The equation MUST be in standard form -You will know to use this method – when x = 0, you get y = 0. *** -Always show the gradient Step 1: Get equation into std form Step 2: mark c =. . Step 3: Apply gradient m = … and move from c Eg: On the same set of axes, draw rough graphs of x – 2 y = 0 and y = -2 x y x – 2 y = 0 y = ½x So 0 – 2 y = 0 Y-int, x=0. So – 2 y = 0 2 -2 -2 1 x So y = 0 *** 0 Step 1: std form -2 y = -x Step 2: c=0 Step 3: SO -2 y = -x -2 -2 y = ½x 1 m = --2 3

Step 1: Get equation into std form Step 2: mark c =. . Step 3: Apply gradient m = … and move from c Eg: On the same set of axes, draw rough graphs of x – 2 y = 0 and y = -2 x y x – 2 y = 0 y = ½x Y-int, x=0. So 0 – 2 y = 0 So – 2 y = 0 2 -2 -2 1 x So y = 0 *** 0 2 Step 1: std form -2 y = -x SO -2 y = -x y = ½x 1 -2 -2 y = – 2 x Step 2: c = 0 y = – 2 x 1 y-int, x=0. So y = 0 *** Step 3: m = --2 Step 1: std form Step 2: c=0 Step 3: 2 m = - --1 y = – 2 x 4

Special Lines: 1. Horizontal and Vertical Graphs: y = c cuts y-axis at c. NB: m = 0 and x = k cuts x-axis at k. NB: m is infinitely large Eg: On the same set of axes, draw rough graphs of y = 2 and x = -3. y = c e. g. y = 2 no matter what x is. y is always 2. NB: mark 2 on y-axis, and show parallel to x-axis x = k e. g. x = - 3 no matter what y is. X is always -3. NB: mark – 3 on x-axis and show parallel to y-axis y x=-3 2 -3 y=2 x 5

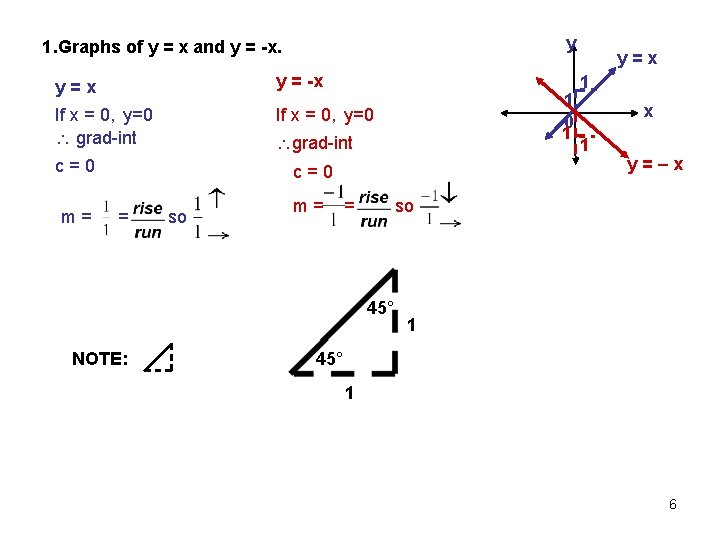
y 1. Graphs of y = x and y = -x. y=x y = -x If x = 0, y=0 grad-int If x = 0, y=0 grad-int c=0 m= 1 0 1 c=0 = so m= = 1 x 1 y=–x so 45° NOTE: y=x 1 45° 1 6

d y Finding the Equation of a Straight Line a STEPS: i write y = mx + c ii c= 2 c -3 iii m= iv Subst into y = mx + c 0 4 x 2 1 Worked examples: b Find the equations of a, b, c and d (Use steps i-iv except for types like c and d) a: step 1: y = mx + c step 2: c = 2 b: step 1: y = mx + c step 2: c = 0 2 step 3: m = + -3 2 step 3: m = - -1 step 4: y = - 2 x x+2 c: y = 2 no matter what x is. y is always 2. y=2 d: x = 4 no matter what y is. x is always 4. x=4 7

3. Find the point of intersection of the lines a) y 1 = 2 x and y 2 = - x + 3 They cut where they are equal y 1 = y 2 2 x = - x + 3 2 x + x = 3 3 x = 3 x=1 b) Subst for x in y = 2 x y = 2(1) = 2 (1 ; 2) y 1 = - 2 x and y 2 = - x + 3 They cut where they are equal y 1 = y 2 - 2 x = - x + 3 -2 x + x = 3 -x = 3 x = -3 © Dr Linda & David Emery 2009 Subst for x in y = -2 x y = - 2(-3) = 6 (-3 ; 6) 8