Grade 9 Approximate Solutions To Equations Using Iteration

Grade 9 Approximate Solutions To Equations Using Iteration Find approximate solutions to equations using iteration, including using suffix notation in recursive formulae If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Lesson Plan Lesson Overview Objective(s) Find approximate solutions to equations using iteration, including using suffix notation in recursive formulae Prior Knowledge Rearranging General iterative processes (grade 7) Duration 50 minutes Resources Print slides: 16 - 20 Grade 9 Equipment Progression of Learning What are the students learning? How are the students learning? (Activities & Differentiation) Rearranging an equation into an iterative form. Give students slide 16. Using slides 4 and 5 explain how can rearrange in more than one way. 5 Solve – find approximate solutions using the iteration. By substitution into the iterative formula for find the approximate solution by looking for 2 consecutive iterations to agree according to the question (e. g. 2 decimal places). Demonstrate using slide 6. 15 Students to practice. Give students slide 17 printed. Find approximate solutions to equations using iteration in contextualised problems Give students slide 18 printed. Allow students to work independently and then review the answer collectively using slide 9. 10 Find approximate solutions to equations using iteration in exam questions (from specimen papers) Give students slides 19 and 20. This includes 5 exam questions related to objective. Students need to use notes from lesson to answer the questions. Ensure that all steps are shown. Relate to mark scheme to show the marks are allocated. 20 Next Steps Assessment PLC/Reformed Specification/Target 7/Ratio, Proportion & Rates of Change/Approximate Solutions to Equations Using Iteration

Key Vocabulary Iteration Recursive Solutions Substitute Rearrange Converge

Solving equations using iteration Iteration is a method we can use to solve difficult equations such as x 3 – x + 7=0. Iterative formula is based on a recursive sequence. It means using the previous term (n) to find the next term (n+1) to get closer and closer to the root of the equation. An iterative rearrangement of x³-x+7 = 0 could be xn+1 = (xn 3 + 7)

The Method – Part 1 To use iteration we must rearrange an equation to the form x=g(x). We can arrange it in more than one way. Lets rearrange x 3 – x + 7 = 0 Rearrange to isolate one of the x’s (could be the x or the x³) a) x 3 – x + 7 = 0 x = x 3 + 7 xn+1 = (xn 3 + 7) b) x 3 – x + 7 = 0 x 3 = x - 7 x = 3√(x – 7) xn+1 = 3√(xn – 7) Now we have two iterative formulae

The Method – Part 2 Step 1: Use the iterative formula with x 0=-2. 5 xn+1 = 3√(xn – 7) x 1 = 3√(x 0 – 7) Step 2: Now use x 1 to find x 2, x 3, x 4, x 5, x 6 etc. x 1 = 3√(-2. 5 – 7) x 1 = -2. 1179 x 2 = -2. 08912838 Step 3: Keep repeating the process under the result converges to the root. x 3 =-2. 086927743 x 4 = -2. 086759303 x 5 = -2. 086746409 x 6=-2. 086745422 Step 4: The answer is -2. 0867 to 4. d. p

Practice 1. Find the first five iterations of these iterative formulae starting with x 1 = 2 a) xn+1 = 3 xn + 6 b) xn+1 = 1 -2 xn c) xn+1 = xn – 6 3 2. Starting with x 0 = 3 show that the solution to the iterative formula is x=2. 99 correct to 2. d. p. 3. a) Show that the equation x² -5 x -3=0 can be rearranged into x= √(5 x+3). b) Use the iterative formula xn+1 = √(5 xn +3) starting with x 0= 5 to find the solution correct to 1. d. p.

Practice - Solutions 1. Find the first five iterations of these iterative formulae starting with x 1 = 2 a) xn+1 = 3 xn + 6 a) x 2 = 12, x 3= 42 , x 4 = 132, x 5 = 402, x 6 = 1, 212 b) xn+1 = 1 -2 xn b) x 2 = -3, x 3= 7 , x 4 = -13, x 5 = 27, x 6 = -53 c) xn+1 = xn – 6 c) x 2 = -1. 3333, x 3= -2. 4444 , x 4 = -2. 81481, 3 x 5 = -2. 93827, x 6 = -2. 97942 2. Starting with x 0 = 3 show that the solution to the iterative formula is x=2. 99 correct to 2. d. p. x 1 = 2. 9907, x 2= 2. 9900 , x 3 = 2. 9899, x 4 = 2. 9899 As x 3= x 4 then answer is x=2. 99 correct to 2. d. p. 3. a) Show that the equation x² -5 x -3=0 can be rearranged into x= √(5 x+3). b) Use the iterative formula xn+1 = √(5 xn +3) starting with x 0= 5 to find the solution correct to 1. d. p. b) x 1 = 5. 291502622 x 2= 5. 427477601 a) x 2 – 5 x -3 = 0 x 3= 5. 489753 x 2 = 5 x + 3 x 4 = 5. 518039 x = √(5 x +3) x 5 = 5. 530840 x 6 = 5. 536 Answer 5. 5 to 1. d. p

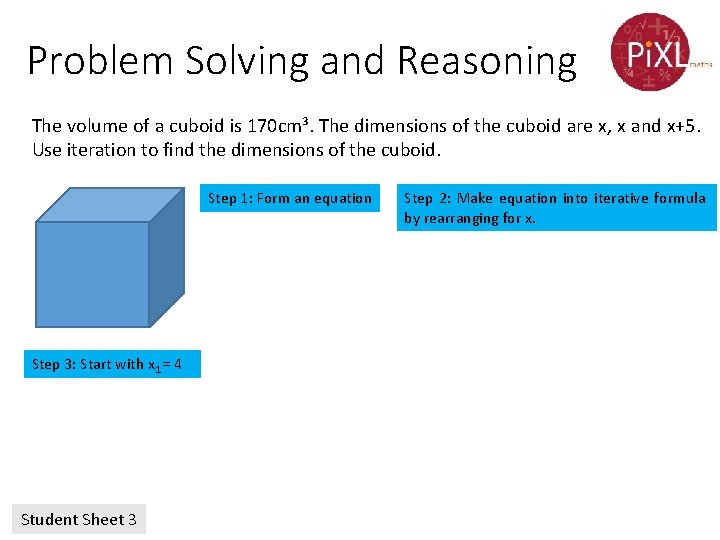
Problem Solving and Reasoning The volume of a cuboid is 170 cm³. The dimensions of the cuboid are x, x and x+5. Use iteration to find the dimensions of the cuboid. Step 1: Form an equation x(x+5)x = 170 x(x²+5 x) = 170 x³+5 x² = 170 Step 3: Start with x 1 = 4 x 2 = 4. 481404747 x 3 = 4. 11312584 x 4 = 4. 403904577 x 5 = 4. 179875808 x 6= 4. 355810989 x 7= 4. 219683743 x 8= 4. 326238443 x 9= 4. 243580707 x 10= 4. 308153161 x 11= 4. 257984192 x 12= 4. 297129021 x 13= 4. 266687075 x 14= 4. 290422292 Step 2: Make equation into iterative formula by rearranging for x. x³ = 170 -5 x² x³ = 170 -5 x² Therefore x=4. 3 to 1. dp

Reason and Explain why solving x³+x=3 is difficult? Will every iteration converge? Explain. Why is the graph of the equation useful in iteration? Does it matter what number you start with? Explore

Exam Questions – Specimen Papers

Exam Questions – Specimen Papers

Exam Questions – Specimen Papers

Exam Questions – Specimen Papers

Exam Questions – Specimen Papers

The Method To use iteration we must rearrange an equation to the form x=g(x). Lets rearrange x 3 – x + 7 = 0 Student Sheet 1

Practice 1. Find the first five iterations of these iterative formulae starting with x 1 = 2 a) xn+1 = 3 xn + 6 b) xn+1 = 1 -2 xn c) xn+1 = xn – 6 3 2. Starting with x 0 = 3 show that the solution to the iterative formula is x=2. 99 correct to 2. d. p. 3. a) Show that the equation x² -5 x -3=0 can be rearranged into x= √(5 x+3). b) Use the iterative formula xn+1 = √(5 xn +3) starting with x 0= 5 to find the solution correct to 1. d. p. Student Sheet 2

Problem Solving and Reasoning The volume of a cuboid is 170 cm³. The dimensions of the cuboid are x, x and x+5. Use iteration to find the dimensions of the cuboid. Step 1: Form an equation Step 3: Start with x 1 = 4 Student Sheet 3 Step 2: Make equation into iterative formula by rearranging for x.

Exam Questions – Specimen Papers - 1 Student Sheet 4

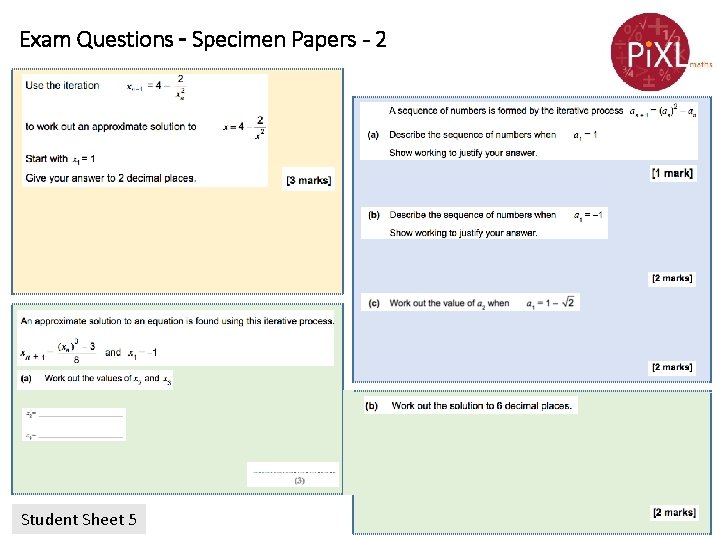
Exam Questions – Specimen Papers - 2 Student Sheet 5