Grade 8 Exponential graphs Recognise sketch and interpret

Grade 8 Exponential graphs Recognise, sketch and interpret graphs of exponential functions y = kx for positive k Plot and interpret exponential real-life graphs to find approximate solutions to real life problems If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Lesson Plan Lesson Overview Objective(s) Recognise, sketch and interpret graphs of exponential functions y = k x for positive k Plot and interpret exponential real-life graphs to find approximate solutions to real life problems Prior Knowledge Indices Solving equations Duration 40 minutes Resources Print slides: 15 - 20 Grade 8 Equipment Progression of Learning What are the students learning? How are the students learning? (Activities & Differentiation) Features of exponential graphs Give students slide 15 printed. Using slides 4 and 5. Discuss the key features of exponential graphs. 5 Plotting an exponential graph Demonstrate how to plot using slide 6. Students to plot y = 4 x. 5 Practice recognise, sketch and interpret graphs and solving exponential functions. Give students slide 16, 17 and 18. Complete practice questions related to the different aspects of exponential graphs. 20 Give students slide 19 – contextualised exponential grow question. Solution on slide 11 and 12. Exponential graphs in exam questions (from specimen papers) Give students slide 20. This includes 2 exam questions related to objective. Students to use notes from lesson. Ensure that all steps are shown. Relate to mark scheme to show the marks are allocated. Next Steps Assessment PLC/Reformed Specification/Target 8/Algebra/Exponential Graphs 10

Key Vocabulary Exponential Function Asymptote

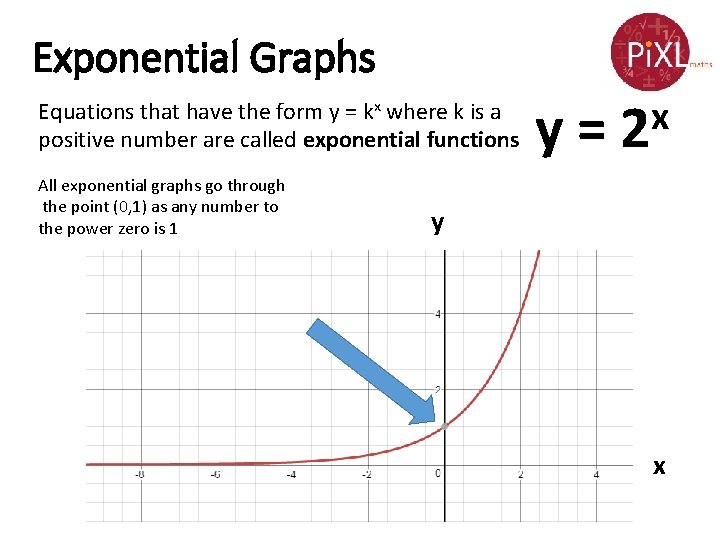
Exponential Graphs Equations that have the form y = kx where k is a positive number are called exponential functions All exponential graphs go through the point (0, 1) as any number to the power zero is 1 y= x 2 y x

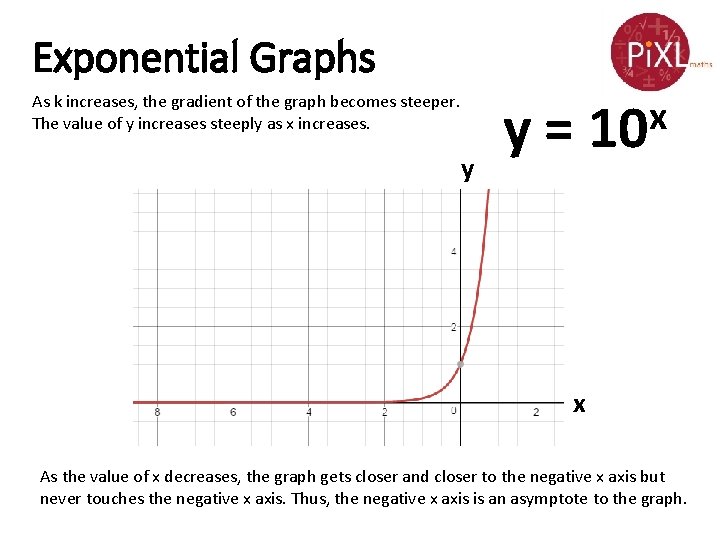
Exponential Graphs As k increases, the gradient of the graph becomes steeper. The value of y increases steeply as x increases. y y= x 10 x As the value of x decreases, the graph gets closer and closer to the negative x axis but never touches the negative x axis. Thus, the negative x axis is an asymptote to the graph.

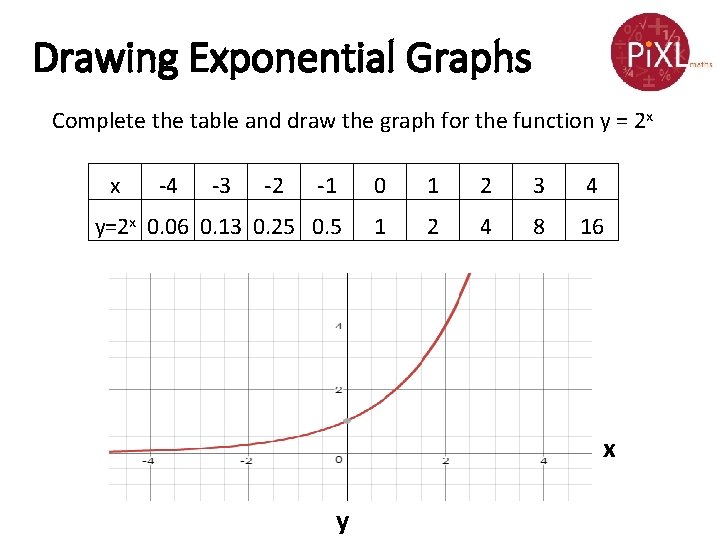
Drawing Exponential Graphs Complete the table and draw the graph for the function y = 2 x x -4 -3 -2 -1 0 1 2 3 4 y=2 x 0. 06 0. 13 0. 25 0. 5 1 2 4 8 16 x y

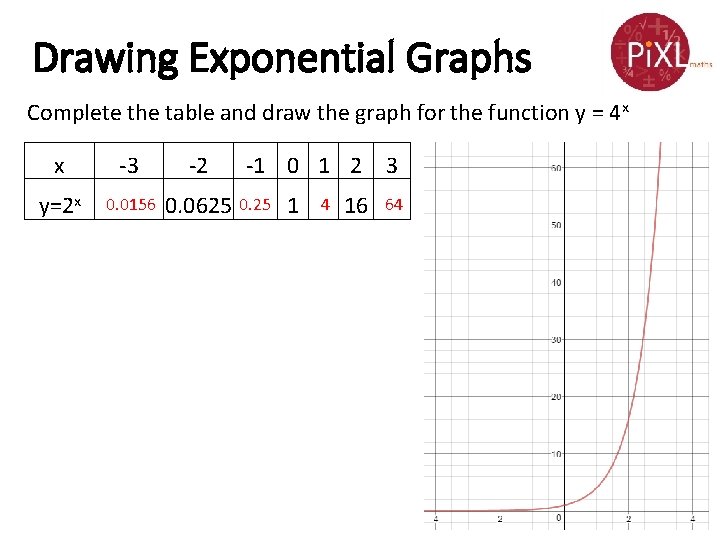
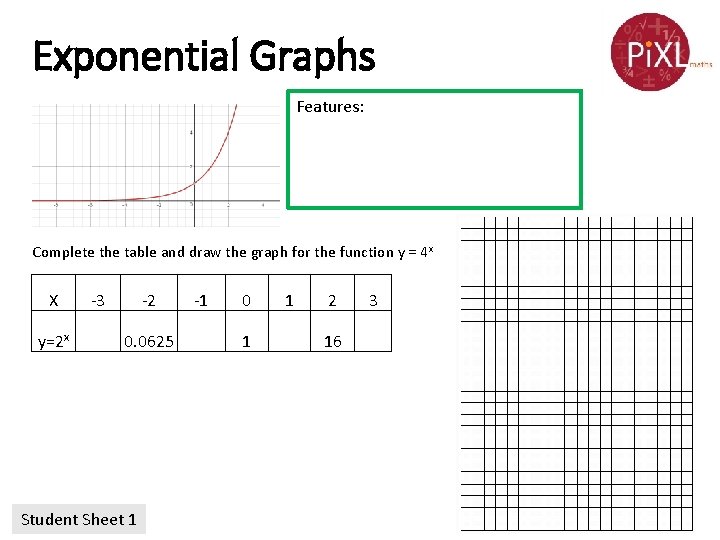
Drawing Exponential Graphs Complete the table and draw the graph for the function y = 4 x x -3 -2 y=2 x 0. 0156 0. 0625 -1 0 1 2 3 0. 25 1 4 16 64

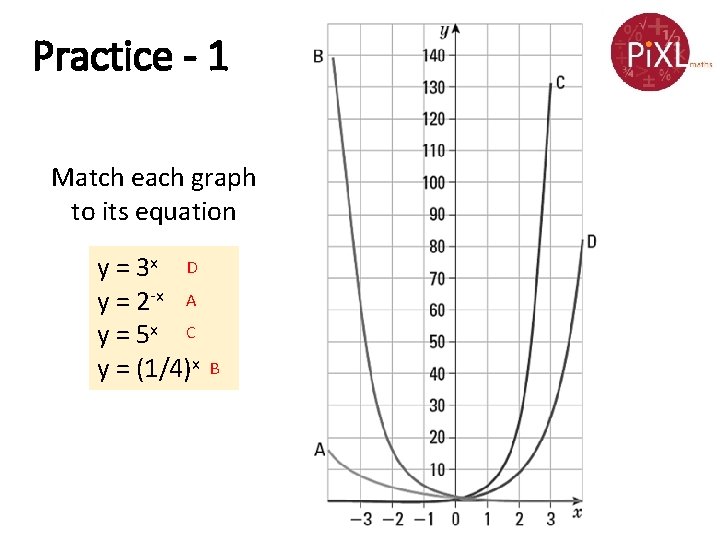
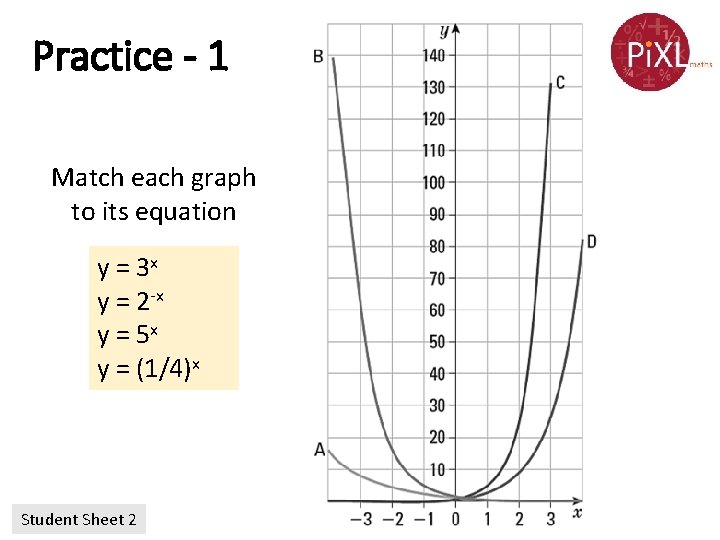
Practice - 1 Match each graph to its equation y = 3 x D y = 2 -x A y = 5 x C y = (1/4)x B

Practice - 2 n = 5 x 20 n=5 x 1 n=5 n = 5 x 26 n = 5 x 64 n = 320 5000 < 5 x 2 y 1000 < 2 y 210 = 1024 29 = 512 10 years to exceed 5000

Practice - 3 100 = m x n 2 100 = 25 x n 2 4 = n 2 25 = m x n 0 25 = m x 1 25 = m 2=n 5 = p x q 1 320 = p x q 4 5=pxq 320 = 5 x q 4 q 5=p q 320 = 5 x q 3 64 = q 3 4=q 5 = p = 1. 25 q

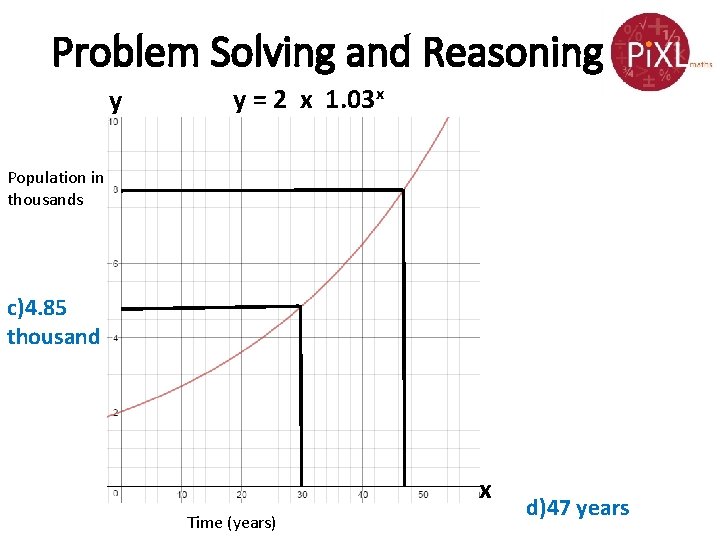
Problem Solving and Reasoning The population of a planet which is currently at two thousand, is growing at a rate of 3 per cent per annum. a) Show that the equation of the expected population, y thousands, in x years time, is given by y = 2 x 1. 03 x b) Draw the graph of y = 2 x 1. 03 x for 0 ≤ x ≤ 50 c) Use your graph to estimate the population in 30 years’ time d) Use your graph to estimate the time taken for the population to reach eight thousand. Current population is at x=0. y = 2 x 1. 030 =2. So the current population is 2 and the multiplier for 3% growth is 1. 03

Problem Solving and Reasoning y y = 2 x 1. 03 x Population in thousands c)4. 85 thousand x Time (years) d)47 years

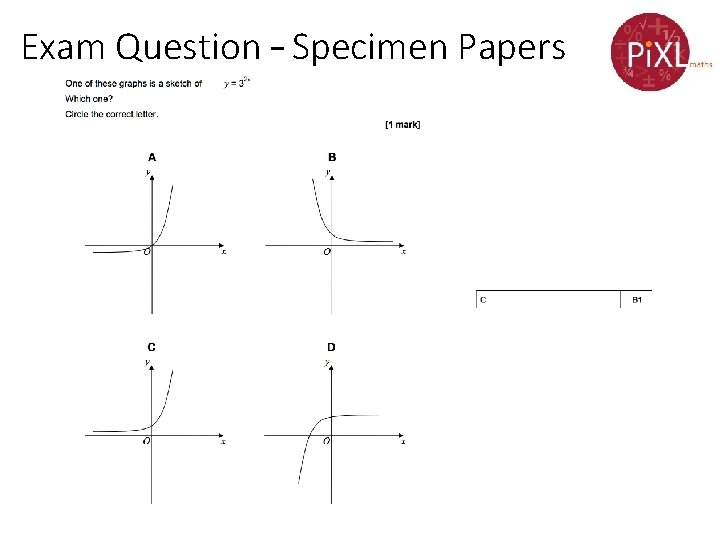
Exam Question – Specimen Papers

Exam Question – Specimen Papers

Exponential Graphs Features: Complete the table and draw the graph for the function y = 4 x X y=2 x -3 -2 0. 0625 Student Sheet 1 -1 0 1 1 2 16 3

Practice - 1 Match each graph to its equation y = 3 x y = 2 -x y = 5 x y = (1/4)x Student Sheet 2

Practice - 2 Student Sheet 3

Practice - 3 Student Sheet 4

Problem Solving and Reasoning The population of a planet which is currently at two thousand, is growing at a rate of 3 per cent per annum. a) Show that the equation of the expected population, y thousands, in x years time, is given by y = 2 x 1. 03 x b) Draw the graph of y = 2 x 1. 03 x for 0 ≤ x ≤ 50 c) Use your graph to estimate the population in 30 years’ time d) Use your graph to estimate the time taken for the population to reach eight thousand. Student Sheet 5

Exam Question – Specimen Papers Student Sheet 6