Grade 7 Ratio Rate Exponents Term 1 Presenters







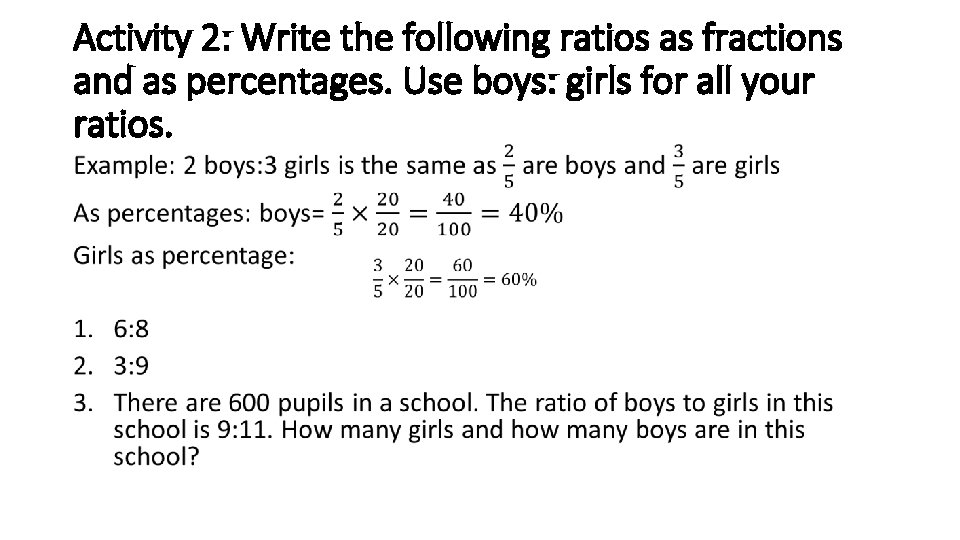
























- Slides: 40

Grade 7 Ratio, Rate & Exponents Term 1 Presenters: Letshabo Lefakane(GW) & Andile Jaxa(SE)

Ratio & Rate – Phase Overview Grade 7 Grade 8 Grade 9 • comparing two or more • ratio and rate quantities of the same kind • direct and kind (ratio) indirect • comparing two quantities of proportion of different kinds (rate) • sharing in a given ratio where the whole is given • increasing or decreasing of a number in a given Ratio

Whole Numbers - Solving problems Solve problems involving whole numbers, including: ØComparing of two or more quantities of the same kind (ratio) ØComparing two quantities of different kinds (rate) ØSharing in a given ratio where the whole is given

Prior Knowledge What are the learners’ presumed prior knowledge, i. e. before engaging learners with Ratio and Rate, what should be their basic knowledge? • HCF & LCM • Fractions • Percentage • Prime numbers

Teaching guidelines • The concepts of ratio and rate are extremely important. A useful way to clarify the difference between rate and ratio is to consider a situation where two objects move at different constant speeds, say 120 km/h and 40 km/h. Each of the speeds is a rate, and the two speeds are in the ratio 3 : 1. In this case, a ratio is a relationship between two rates. • 120 km/h and 40 km/h are rates • Comparing the 2 rates above: 120: 40 simplified to 3: 1 (both divided by 40) - ratio

Ratio •

Ratios can be shown in different ways: • using the ": " to separate example values • using the "/" to separate one value from the total • as a decimal, after dividing one value by the total • as a percentage, after dividing one value by the total Example: if there is 1 boy and 3 girls you could write the ratio as: 1: 3 (for every one boy there are 3 girls) 1/4 are boys and 3/4 are girls 0. 25 are boys (by dividing 1 by 4) 25% are boys (0. 25 as a percentage)

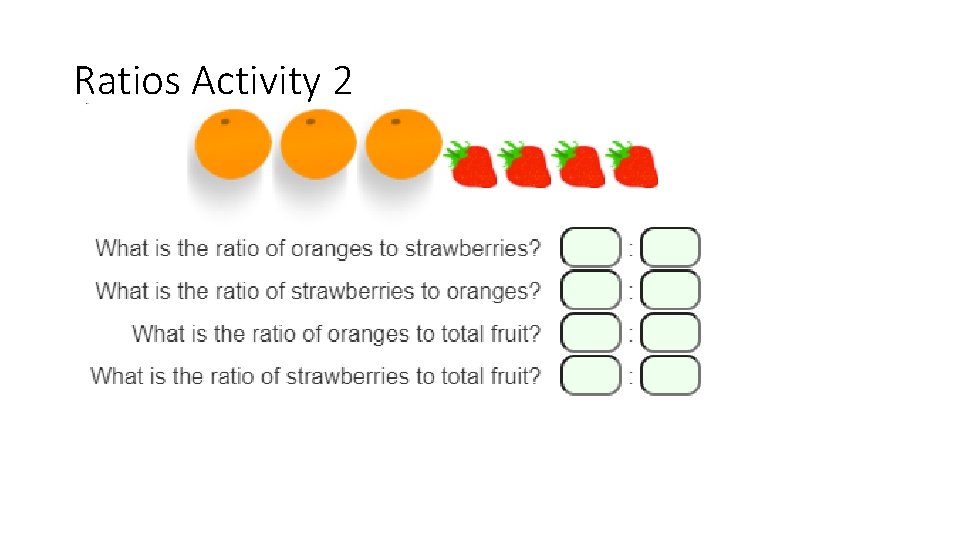
Ratios Activity 2
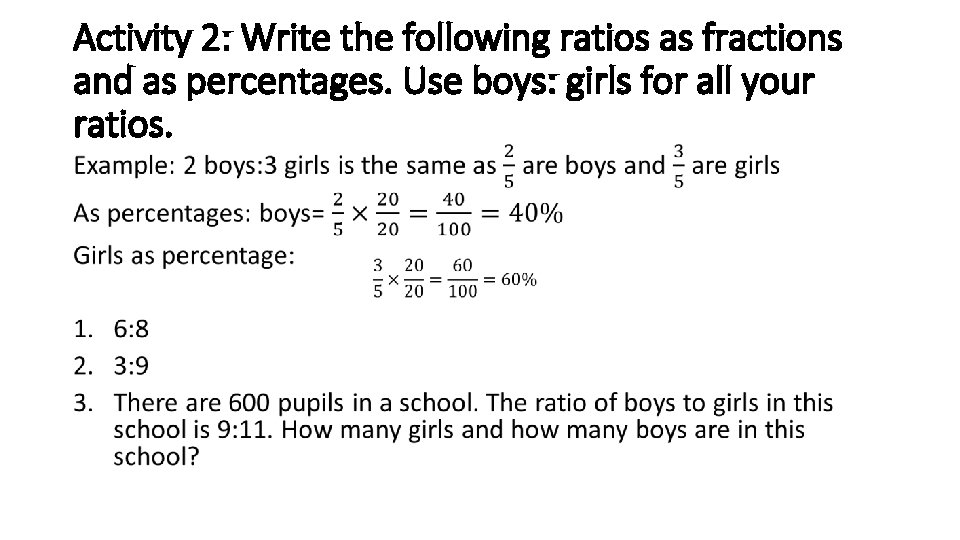
Activity 2: Write the following ratios as fractions and as percentages. Use boys: girls for all your ratios. •

ACTIVITY 3: SHARING IN A GIVEN RATIO • Nathi, Paul and Tim worked in Mr Setati’s garden. Nathi worked for five hours, Paul for four hours and Tim for three hours. Mr Setati gave the boys R 600 for their work. How should they divide the R 600 among the three of them? • Nathi = 5 hrs • Paul = 4 hrs • Tim = 3 hrs • Ratio>>> 5: 4: 3 with total hours of 5+4+3=12 hrs • Meaning: Divided into 12 equal parts(hours), and workers will be remunerated according to the time spent on the work

SIMPLIFYING RATIOS • Ratio can be written in its simplest form. We simplify ratios by dividing both quantities by the same factor. Example: Jabu gets 85% for his test and Musa gets 17% Write the ratio in words Write the ratio mathematically. (the ratio is not in its simplest form) To simplify, divide both quantities by the HCF (17). Then write the final answer Musa’s mark: Jabu’s mark

SHARING IN A GIVEN RATIO •

Increasing or Decreasing a number in a given ratio •

Rate Activity 5: Discuss the definitions below • rate(noun) a magnitude or frequency relative to a time unit e. g. -"they travelled at a rate of 55 km per hour"; "the rate of change was faster than expected" • rate (noun) amount of a charge or payment relative to some basis e. g. -"a 10 -minute phone call at that rate would cost R 5" • rate(noun) the relative speed of progress or change e. g. -"he lived at a fast pace"; "he works at a great rate"; "the pace of events accelerated“ • A rate compares quantities of different kinds.

Examples: Use of Rate in daily occurrences •

Activity 5 Problem Solving •

Activity 6 -Ratio & rate Misconceptions/Errors •

Common Misconceptions and How to Prevent Them Misconceptions Examples for Preventing or Correcting Some learners believe ratios always compare a part to a whole, like fractions. Provide an example in which learners compare a part to a part (e. g. , 1 green apple to 3 red apples). Explain that ratios can compare part to part, not only part to whole. The ratio 1 to 3 compares part of the apples to another part of the apples Some learners struggle to simplify ratios. Demonstrate an example of simplification, explicitly describing the steps: 1. Check for common factors. (The easiest thing to remember is to use the prime numbers 2, 3, 5, 7, and 11. ) 2. Divide each part of the ratio by the common factor. Some learners believe that ratios and rates can always be simplified to a mixed number or a whole number.

• • • Key Ideas Ratios describe the relationship between quantities with the same unit. Ratios can be generated to represent situations in real life. Ratios compare quantities and can be simplified like fractions. Rates compare unlike quantities. Rates can be simplified like ratios, using common factors. A unit rate describes how many units there are of the first quantity for 1 unit of the second quantity. Equivalent ratios describe the same relationship between objects, which means they can be simplified to the same ratio. Multiplication can be used to generate equivalent ratios. Unit rates can be generated by using a table. Equivalent rates can be generated by calculating the unit rate and then multiplying to find the equivalent rate. Rates can be compared by calculating and comparing the unit rates.

EXPONENTS (Grade 7 CAPS page 43 -44) •

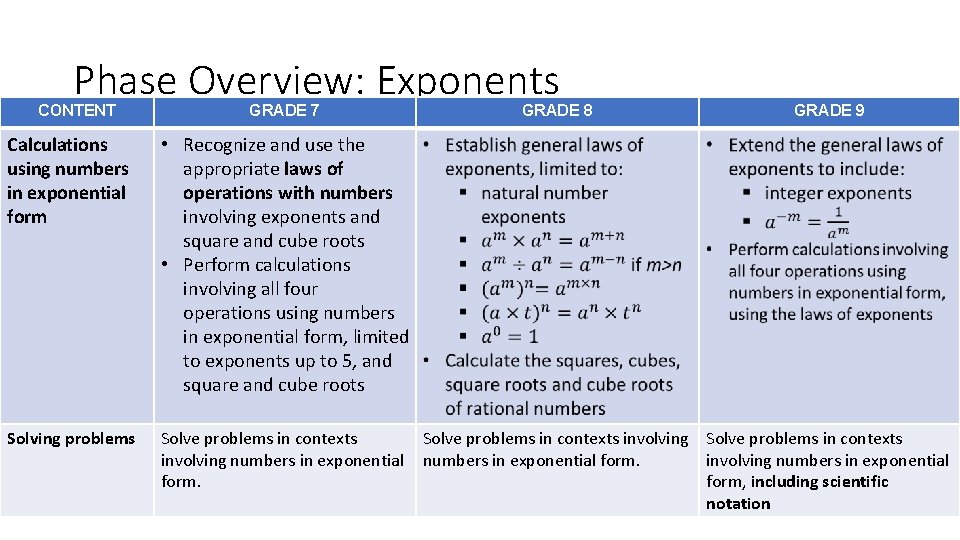
Phase Overview: Exponents CONTENT GRADE 7 GRADE 8 GRADE 9 Mental calculations Comparing and representing numbers in exponential form • Compare and represent • Extend scientific integers in exponential notation to include form negative exponents • Compare and represent numbers in scientific notation, limited to positive exponents

Phase Overview: Exponents CONTENT GRADE 7 Calculations using numbers in exponential form • Recognize and use the appropriate laws of operations with numbers involving exponents and square and cube roots • Perform calculations involving all four operations using numbers in exponential form, limited to exponents up to 5, and square and cube roots Solving problems Solve problems in contexts involving numbers in exponential form. GRADE 8 GRADE 9 Solve problems in contexts involving Solve problems in contexts numbers in exponential form. involving numbers in exponential form, including scientific notation

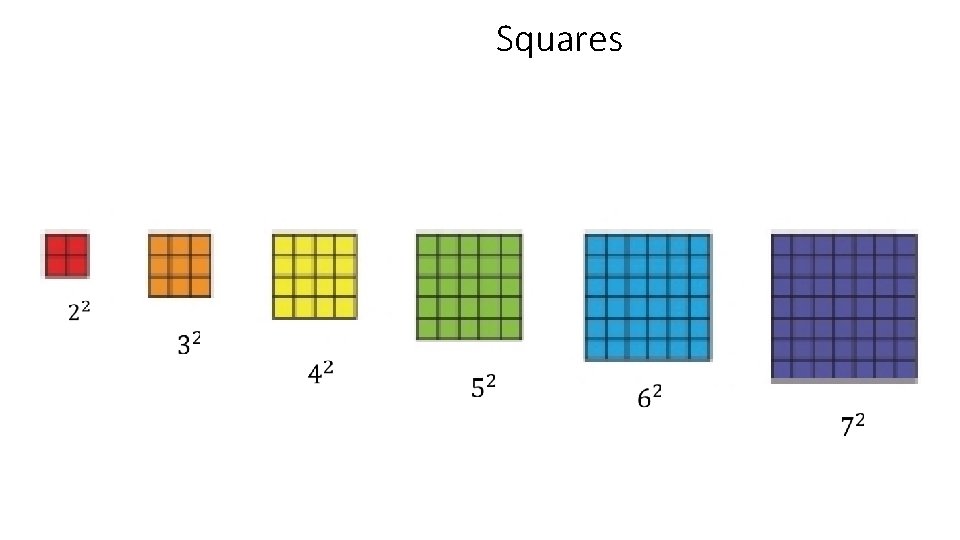
Prior Knowledge(Refer to page 43 of CAPS) • Do learners know what exponents are? • Can the learners differentiate (if there is any difference) between a power and an exponent/index? • Which concepts were taught in Grade 6 that should make it easier for learners to understand exponents? Although learners may have encountered square numbers in Grade 6, they were not expected to write these numbers in exponential form.

Squares

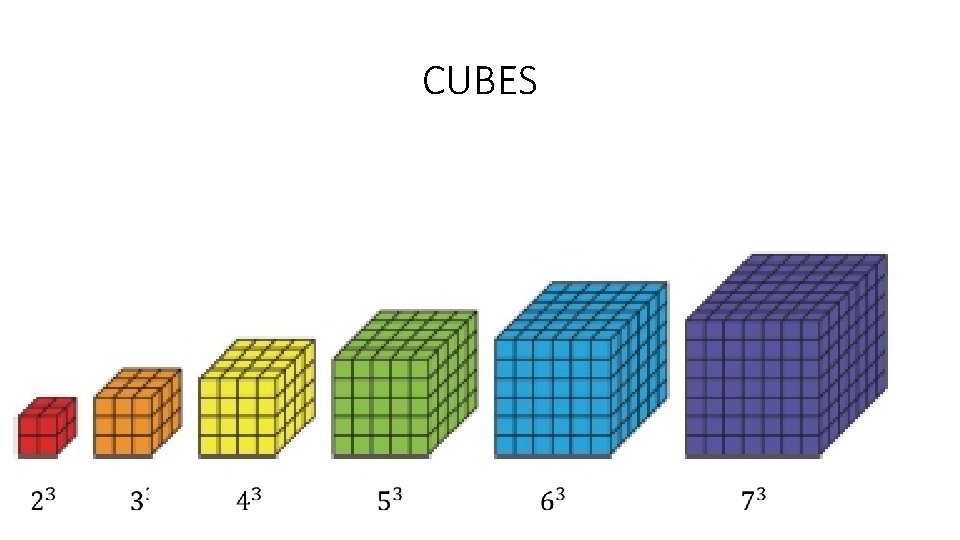
CUBES

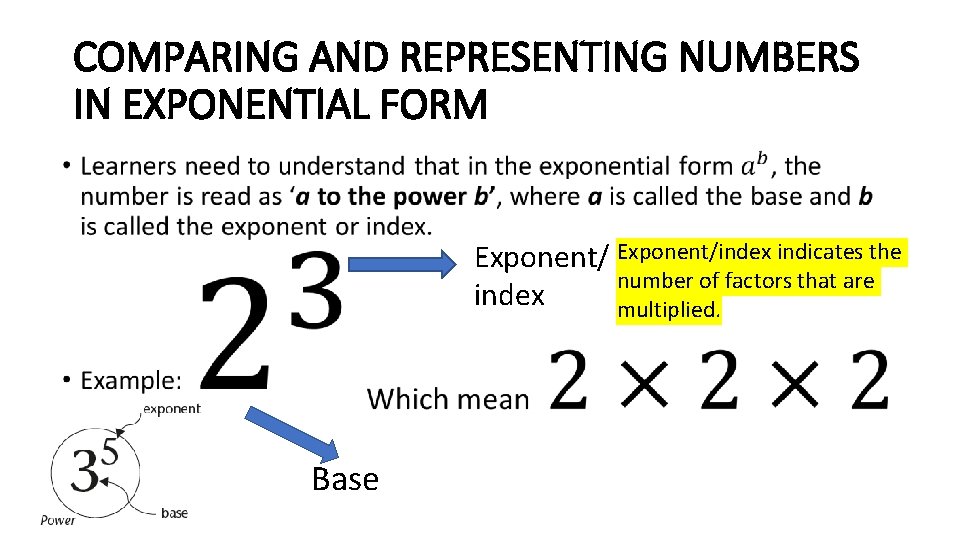
COMPARING AND REPRESENTING NUMBERS IN EXPONENTIAL FORM • Exponent/index indicates the number of factors that are index multiplied. Base

Exponents: Introduction-Teaching Strategy •

Activity 6: Comparing and Representing numbers in Exponential form • 1. What is the biggest number you can make with the symbols 4 and 2? 2. Is the difference between the squares of two consecutive whole numbers always an odd number?

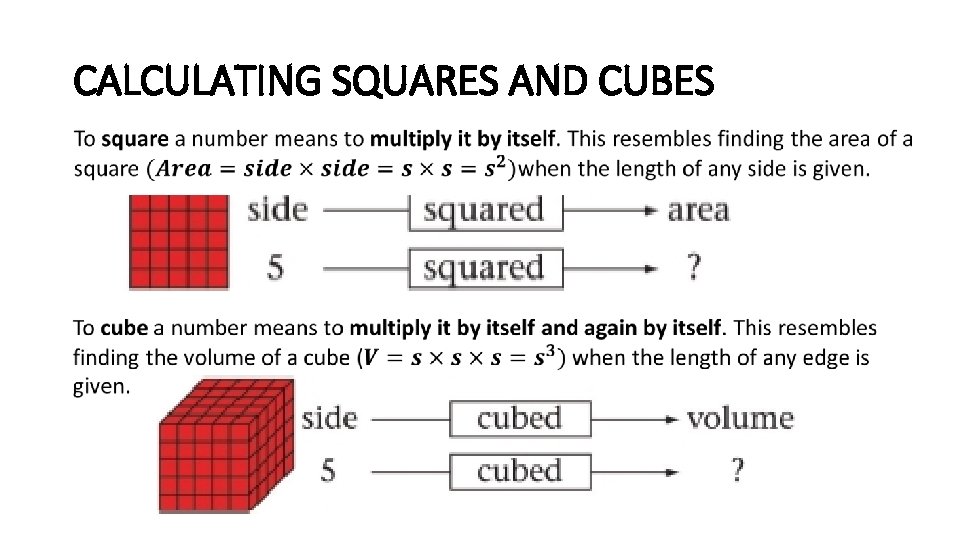
CALCULATING SQUARES AND CUBES •

CALCULATING SQUARES AND CUBES

Activity 7: Are the following numbers squares, cubes, both or neither? Compare your answers with the answers of other participants. a) b) c) d) e) f) g) h) i) 64 1 121 1 000 512 400 65 216 169 both square cube square neither cube square

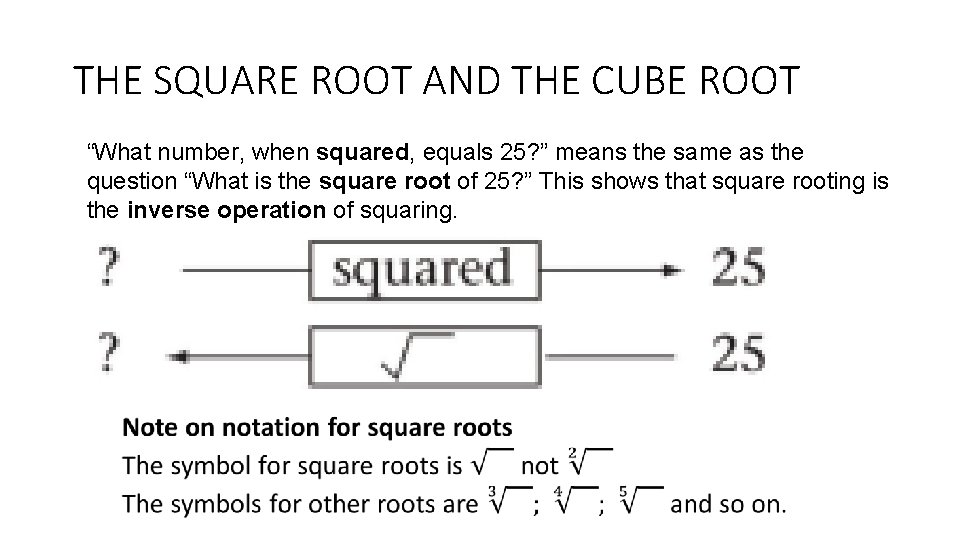
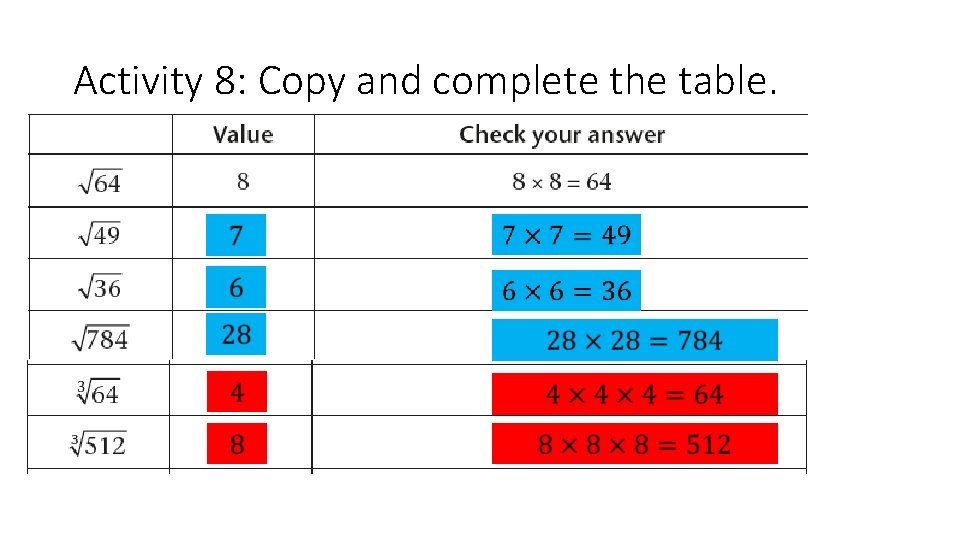
THE SQUARE ROOT AND THE CUBE ROOT “What number, when squared, equals 25? ” means the same as the question “What is the square root of 25? ” This shows that square rooting is the inverse operation of squaring.

THE SQUARE ROOT AND THE CUBE ROOT

Activity 8: Copy and complete the table.

COMPARING NUMBERS IN EXPONENTIAL FORM • Use the symbols =, < or > to make the following true. = > < < < = < <

COMPARING NUMBERS IN EXPONENTIAL FORM • In questions (a) to (d), arrange the numbers in descending order:

CALCULATIONS WITH EXPONENTS • Important to note when doing calculations involving exponents: q. The acronym BIDMAS stands for Brackets; Indices (which imply powers), Division/Multiplication from left to right, and Addition/Subtraction from left to right. This indicates that powers should usually be worked out before division and multiplication (which includes “Of”). • The base should be simplified before the exponent is applied. • It is important to know the correct order in which operations in a numerical expression should be done.

Activity 9: Do these calculations without using a calculator. (page 48 LB) After doing the calculations: Discuss the envisaged misconceptions or errors learners might have (or might commit) while calculating and how best to avoid or to help learners to overcome these.

Misconceptions: Exponents •

Misconceptions (cont. ) •