Grade 7 Alignment to Mathematics GradeLevel Standards Session

Grade 7: Alignment to Mathematics Grade-Level Standards

Session Objective The purpose of these materials is to help develop understanding of the expectations of high-quality summative assessment items. The concepts shown throughout these modules can be useful for classroom questioning and assessment, but the items themselves may need to be slightly modified. PAGE 2

CCSSO Section C: Align to Standards – Mathematics Criterion C. 1: Focusing strongly on the content most needed for success in later mathematics Criterion C. 2: Assessing a balance of concepts, procedures, and applications Criterion C. 3: Connecting practice to content Criterion C. 4: Requiring a range of cognitive demand Criterion C. 5: Ensuring high-quality items and a variety of item types PAGE 3

PAGE 4

Ten Principles of CCSS-Aligned Items 1. Most items aligned to standards in supporting clusters connect to the major work of the grade. 2. Items are designed to address the aspect(s) of rigor (conceptual understanding, procedural skill, and application) evident in the language of the content standards. 3. Items are designed to attend to content limits articulated in the standards. 4. Most items aligned to a single content standard should assess the central concern of the standard. 5. Representations are well suited to the mathematics that students are learning and serve an important purpose within the item itself. 6. Items use mathematically precise language, are free from mathematical errors or ambiguities, and are aligned to the mathematically appropriate standard. 7. The demands of items measuring the Standards for Mathematical Practice are appropriate to the targeted grade level. 8. Item types are chosen to match the item’s purpose and as part of the evidence required by the standards. 9. Most items measuring the Standards for Mathematical Practice are also aligned to content standards representing the major work of the grade. 10. Items written at the cluster or domain level measure key integration points not necessarily articulated in individual standards but plausibly implied directly by what is written. PAGE 5

Alignment Principle #1 Most items aligned to standards in supporting clusters connect to the major work of the grade. PAGE 6

Most items aligned to standards in supporting clusters connect to the major work of the grade. Nanette is creating a scale drawing of a statue. The statue has a height of 5 feet. The scale drawing will use a height of ¾ foot. What scale factor does Nanette need to apply to the statue to create the scale drawing? 7. G. A. 1 Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale. PAGE 7

Alignment Principle #2 Items are designed to address the aspect(s) of rigor (conceptual understanding, procedural skill, and application) evident in the language of the content standards. PAGE 8

Items are designed to address the aspect(s) of rigor (conceptual understanding, procedural skill, and application) evident in the language of the content standards. 7. RP. A Analyze proportional relationships and use them to solve realworld and mathematical problems. PAGE 9

Items are designed to address the aspect(s) of rigor (conceptual understanding, procedural skill, and application) evident in the language of the content standards. 7. NS. A. 1 Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram. PAGE 10

Items are designed to address the aspect(s) of rigor (conceptual understanding, procedural skill, and application) evident in the language of the content standards. 7. NS. A. 2 d. Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0 s or eventually repeats. PAGE 11

Items are designed to address the aspect(s) of rigor (conceptual understanding, procedural skill, and application) evident in the language of the content standards. 7. EE. B. 3 Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies. PAGE 12

Alignment Principle #3 Items are designed to attend to content limits articulated in the standards. PAGE 13

Items are designed to attend to content limits articulated in the standards. Linda has $26. She earns $6 for each hour of babysitting. Write an equation for t, the total amount of money Linda has after babysitting for h hours. Linda has $26. She earns $6 for each hour of babysitting. She wants to buy a ski pass for $80. Enter the minimum number of hours Linda must babysit to be able to buy the ski pass. 7. EE. B. 4. a. Solve word problems leading to equations of the form px+q=r and p(x+q)=r, where p, q, and r are specific rational numbers. Solve equations of these forms fluently. Compare an algebraic solution to an arithmetic solution, identifying the sequence of operations used in each approach. PAGE 14

Alignment Principle #4 Most items aligned to a single content standard should assess the central concern of the standard. PAGE 15

Most items aligned to a single content standard should assess the central concern of the standard. Not the Central Concern For each set of 3 lengths given, select YES or NO to tell whether they could be the side lengths of a triangle. Lengths YES NO Use the line segment tool to create a regular hexagon in the space provided. You may use the ruler and/or protractor tools as needed. 5 cm, 4 cm, 3 cm 7 cm, 5 cm, 1 cm 12 cm, 6 cm 7. G. A. 2 Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle. PAGE 16

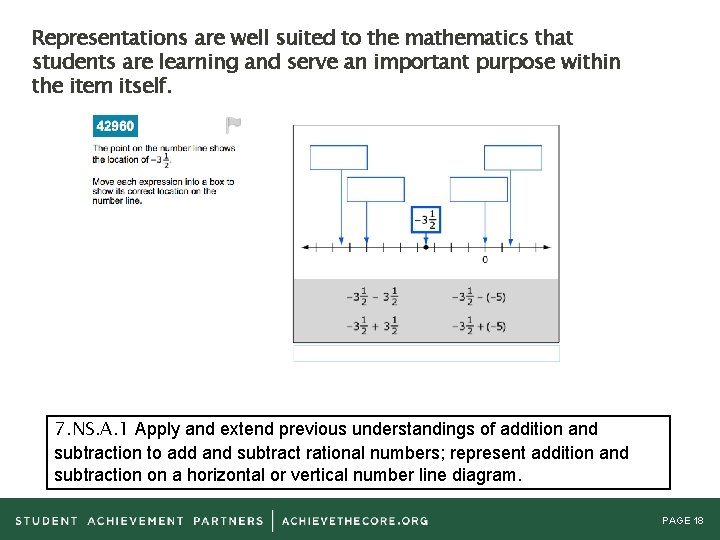
Alignment Principle #5 Representations are well suited to the mathematics that students are learning and serve an important purpose within the item itself. PAGE 17

Representations are well suited to the mathematics that students are learning and serve an important purpose within the item itself. 7. NS. A. 1 Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram. PAGE 18

Alignment Principle #6 Items use mathematically precise language, are free from mathematical errors or ambiguities, and are aligned to the mathematically appropriate standard. PAGE 19

Items use mathematically precise language, are free from mathematical errors or ambiguities, and are aligned to the mathematically appropriate standard. ✗ Jorge has $50. He works for x number of hours and makes $20 per hour. Write an equation that can be solved to find the number of hours he needs to work to have a total of $310. ✔ Jorge has $50. He works for x hours and makes $20 per hour. Write an equation that can be solved to find the number of hours he needs to work to have a total of $310. 6. RP. A. 3 Use ratio and rate reasoning to solve realworld and mathematical problems, e. g. , by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. PAGE 20

Alignment Principle #7 The demands of items measuring the Standards for Mathematical Practice are appropriate to the targeted grade level. PAGE 21

The demands of items measuring the Standards for Mathematical Practice are appropriate to the targeted grade level. MP 4. Model with mathematics. 7. RP. A. 3. Use proportional relationships to solve multistep ratio and percent problems. PAGE 22

Alignment Principle #8 Item types are chosen to match the item’s purpose and as part of the evidence required by the standards. PAGE 23

Item types are chosen to match the item’s purpose and as part of the evidence required by the standards. For each row, click the box that correctly compares the values of A and B. A B A>B A<B A=B 7. NS. A. 1 Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram. PAGE 24

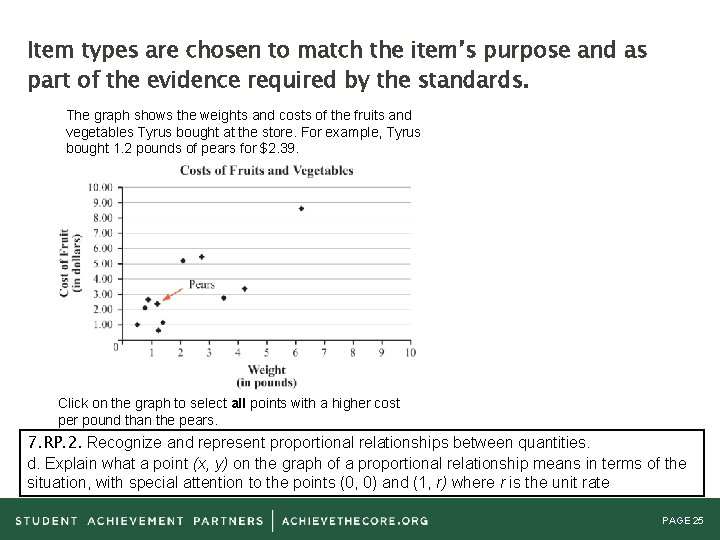
Item types are chosen to match the item’s purpose and as part of the evidence required by the standards. The graph shows the weights and costs of the fruits and vegetables Tyrus bought at the store. For example, Tyrus bought 1. 2 pounds of pears for $2. 39. Click on the graph to select all points with a higher cost per pound than the pears. 7. RP. 2. Recognize and represent proportional relationships between quantities. d. Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate PAGE 25

Item types are chosen to match the item’s purpose and as part of the evidence required by the standards. 7. NS. A. 1. c. Understand subtraction of rational numbers as adding the additive inverse, p – q = p + (–q). Show that the distance between two rational numbers on the number line is the absolute value of their difference, and apply this principle in real-world contexts. 7. EE. A. 1. Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients. PAGE 26

Alignment Principle #9 Most items measuring the Standards for Mathematical Practice are also aligned to content standards representing the major work of the grade. PAGE 27

Most items measuring the Standards for Mathematical Practice are also aligned to content standards representing the major work of the grade. MP 4. Model with mathematics. 7. RP. A. Analyze proportional relationships and use them to solve real-world and mathematical problems. PAGE 28

Alignment Principle #10 Items written at the cluster or domain level measure key integration points not necessarily articulated in individual standards but plausibly implied directly by what is written. PAGE 29

Items written at the cluster or domain level measure key integration points not necessarily articulated in individual standards but plausibly implied directly by what is written. 7. RP. A Analyze proportional relationships and use them to solve real-world and mathematical problems. PAGE 30

Ten Principles of CCSS-Aligned Items 1. Most items aligned to standards in supporting clusters connect to the major work of the grade. 2. Items are designed to address the aspect(s) of rigor (conceptual understanding, procedural skill, and application) evident in the language of the content standards. 3. Items are designed to attend to content limits articulated in the standards. 4. Most items aligned to a single content standard should assess the central concern of the standard. 5. Representations are well suited to the mathematics that students are learning and serve an important purpose within the item itself. 6. Items use mathematically precise language, are free from mathematical errors or ambiguities, and are aligned to the mathematically appropriate standard. 7. The demands of items measuring the Standards for Mathematical Practice are appropriate to the targeted grade level. 8. Item types are chosen to match the item’s purpose and as part of the evidence required by the standards. 9. Most items measuring the Standards for Mathematical Practice are also aligned to content standards representing the major work of the grade. 10. Items written at the cluster or domain level measure key integration points not necessarily articulated in individual standards but plausibly implied directly by what is written. PAGE 31

Thank You!