Grade 5 Derive an equation or two simultaneous

Grade 5 Derive an equation (or two simultaneous equations), solve the equation(s) and interpret the solution in context If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Key Vocabulary Derive Formulae Expression Equation Algebra Unknown Variable

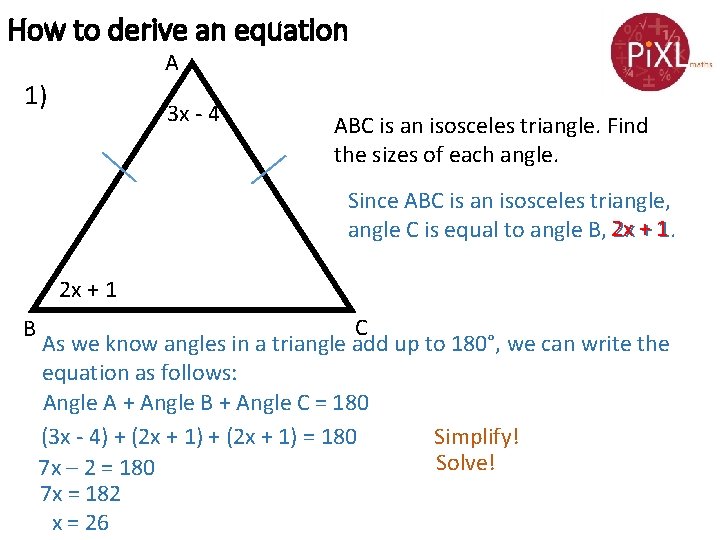
How to derive an equation A 1) 3 x - 4 ABC is an isosceles triangle. Find the sizes of each angle. Since ABC is an isosceles triangle, angle C is equal to angle B, 2 x + 11. 2 x + 1 B C As we know angles in a triangle add up to 180°, we can write the equation as follows: Angle A + Angle B + Angle C = 180 Simplify! (3 x - 4) + (2 x + 1) = 180 Solve! 7 x – 2 = 180 7 x = 182 x = 26

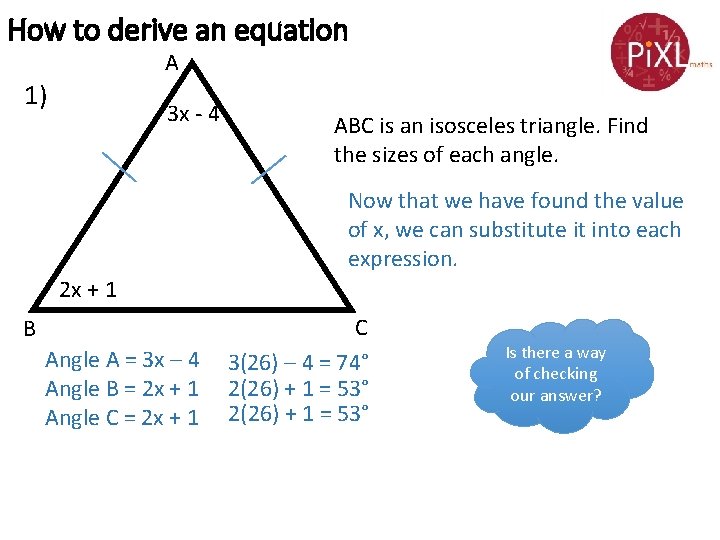
How to derive an equation A 1) 3 x - 4 ABC is an isosceles triangle. Find the sizes of each angle. Now that we have found the value of x, we can substitute it into each expression. 2 x + 1 B Angle A = 3 x – 4 Angle B = 2 x + 1 Angle C = 2 x + 1 C 3(26) – 4 = 74° 2(26) + 1 = 53° Is there a way of checking our answer?

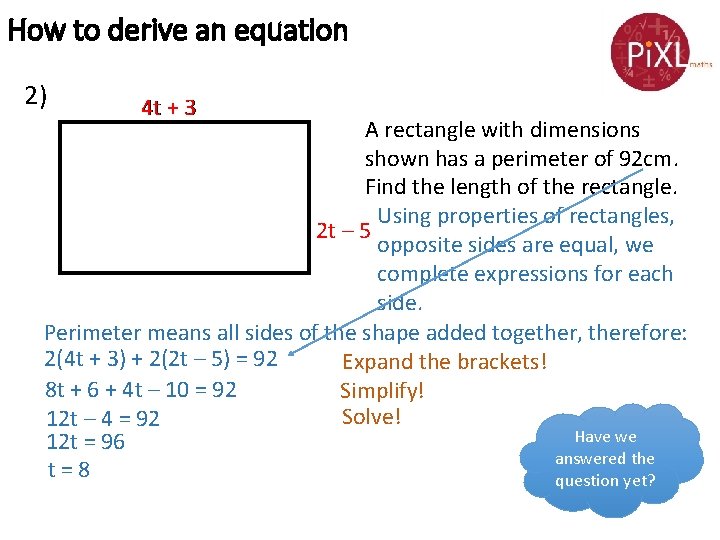
How to derive an equation 2) 4 t + 3 A rectangle with dimensions shown has a perimeter of 92 cm. Find the length of the rectangle. Using properties of rectangles, 2 t – 5 opposite sides are equal, we complete expressions for each side. Perimeter means all sides of the shape added together, therefore: 2(4 t + 3) + 2(2 t – 5) = 92 Expand the brackets! 8 t + 6 + 4 t – 10 = 92 Simplify! Solve! 12 t – 4 = 92 Have we 12 t = 96 answered the t=8 question yet?

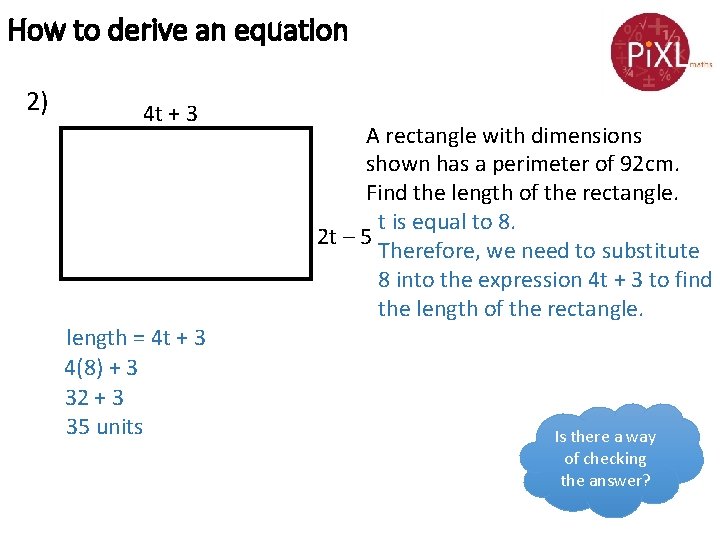
How to derive an equation 2) 4 t + 3 length = 4 t + 3 4(8) + 3 32 + 3 35 units A rectangle with dimensions shown has a perimeter of 92 cm. Find the length of the rectangle. t is equal to 8. 2 t – 5 Therefore, we need to substitute 8 into the expression 4 t + 3 to find the length of the rectangle. Is there a way of checking the answer?

How to derive an equation 3) Five sandwiches and four drinks cost £ 20. Two sandwiches and five drinks cost £ 8. Find the cost for one sandwich. We can call sandwiches ‘s’ and drinks ‘d’. 5 s + 4 d = 20 x 5 x 4 2 s + 5 d = 8 Solve! 25 s + 20 d = 100 _ 8 s + 20 d = 32 17 s s = 68 =4 Can we calculate the cost for one drink?

Derive equations – now you try. . . a) A rectangle has a perimeter of 32 cm. Its length is 4 cm longer than its width. What is its width? b) A rectangle has an area of 50 cm 2. Its length is double its width. Find the perimeter. c) A shirt and two trousers cost £ 20. Four shirts and two trousers cost £ 50. Find the price difference between the two items.

Derive equations – now you try. . . a) A rectangle has a perimeter of 32 cm. Its length is 4 cm longer than its width. What is its width? w = 6 b) A rectangle has an area of 50 cm 2. Its length is double its width. Find the perimeter. w = 5, l = 10, P = 30 cm c) A shirt and two trousers cost £ 20. Four shirts and two trousers cost £ 50. Find the price difference between the two items. £ 5

Problem Solving and Reasoning a a+1 B 5 a The perimeter of the garden pictured is 48 metres. Jim wants to cover the garden with grass seed. Each pack of grass seed 2 a + 1 can cover 8 m 2 and cost £ 5. 20. How much will it cost to cover the garden? A 5+a (5 + a) + a + 5 + (a + 1) + a + (2 a + 1) = 48 6 a + 12 = 48 a=6 Area of the shape = A = 6 x 11 = 66 m 2 Area of the shape = B = 6 x 13 = 78 m 2 Total area = 66 + 78 = 144 m 2 144 ÷ 8 =18 packets needed 18 x 5. 20 = £ 93. 60

Reason and explain Give an example of an answer which is invalid. If x is three times y, which one is correct: 3 x=y or 3 y=x What skills/prior knowledge do you need to have to master this section?