Grade 4 Multiply single brackets Multiply a single

Grade 4 Multiply single brackets Multiply a single term over a bracket If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Key Vocabulary Bracket Single term Multiply brackets Expand brackets Remove brackets

How to multiply a single bracket ‘Multiply brackets’ means to ‘expand’, or remove the brackets To multiply brackets, multiply everything inside the brackets by what is outside them 4(a + 6) = 4 a + 24 2(3 b - 5 c) = 6 b - 10 c

Multiply a bracket - now you try. . . 1) 3(x + 5) = 2) a(2 b - 3) = 3) -4(y - 9) = 4) 5 d(e – 7 d) =
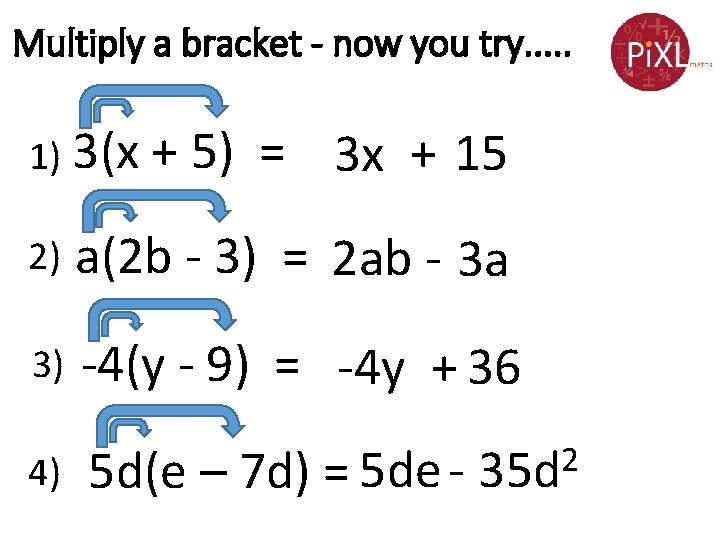
Multiply a bracket - now you try. . . 1) 3(x + 5) = 3 x + 15 2) a(2 b - 3) = 2 ab - 3 a 3) -4(y - 9) = -4 y + 36 4) 5 d(e – 7 d) = 5 de - 2 35 d
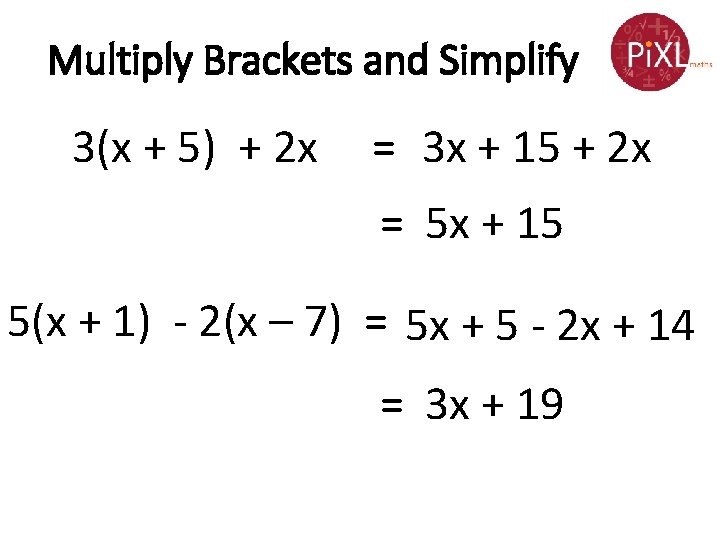
Multiply Brackets and Simplify 3(x + 5) + 2 x = 3 x + 15 + 2 x = 5 x + 15 5(x + 1) - 2(x – 7) = 5 x + 5 - 2 x + 14 = 3 x + 19

Problem Solving and Reasoning Spot the mistakes 1) 3(q + 6) = 3 q + 6 2) 9(p + 4) = p + 36 3) 6(y - 5) = 6 y – 11 4) 8(w - 3) = w + 24 5) -c(c - 4) = c² - 4 + c

Problem Solving and Reasoning Spot the mistakes 1) 3(q + 6) = 3 q + 6 2) 9(p + 4) = p + 36 3) 6(y - 5) = 6 y – 11 4) 8(w - 3) = w + 24 5) -c(c - 4) = c² - 4 + c

Problem Solving and Reasoning x+ 7 3 x Show that the area of this rectangle can be written as 3 x 2 + 21 x.
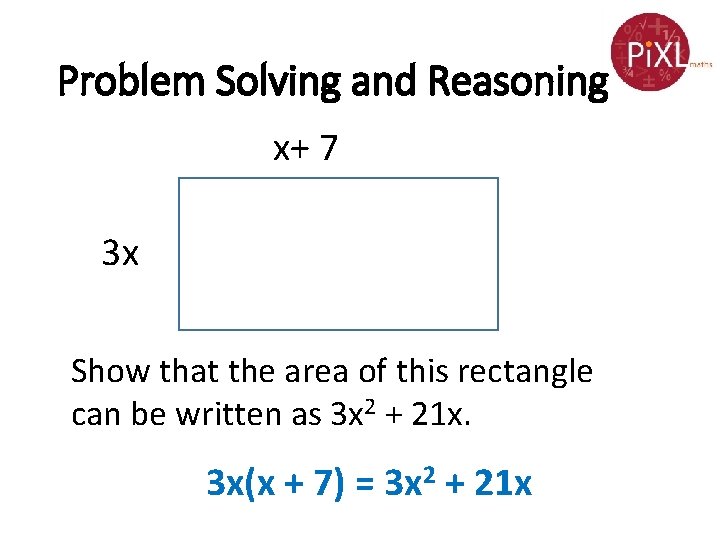
Problem Solving and Reasoning x+ 7 3 x Show that the area of this rectangle can be written as 3 x 2 + 21 x. 3 x(x + 7) = 3 x 2 + 21 x

Problem Solving and Reasoning Explain why (4 x – 5) + x – (5 x – 7) is always equal to 2 whatever the value of x.

Problem Solving and Reasoning Explain why (4 x – 5) + x – (5 x – 7) is always equal to 2 whatever the value of x. (4 x – 5) + x – (5 x – 7) = 4 x – 5 + x – 5 x + 7 = 5 x – 5 x +7 – 5 = 2
- Slides: 12