Grade 12 Physics Knowledge area Mechanics Projectile motion

Grade 12 Physics Knowledge area: Mechanics

Projectile motion 2. 3 Terminal velocity The upward force due to air resistance is just as big as the downward weight. Falls at a constant velocity – terminal velocity. Freefall is when gravitational force is the only force that acts on an object. Definition

Projectile motion 2. 4 Equations of motion • vf = vi + aΔt final velocity (m⋅s-1) • Δx = viΔt + ½aΔt 2 initial velocity (m⋅s-1) • vf 2 = vi 2 + 2 aΔx acceleration (m⋅s-2) • Δx = ½(vi + vf)Δt time (s) vf vi a/g Δt Δx/Δy displacement or position (m) Definition

Projectile motion 2. 5 Problem solving Describe the acceleration, velocity and displacement of a ball that is: a) b) thrown upwards and then caught; dropped (vi = 0 m⋅s-1). Assume upwards is positive.

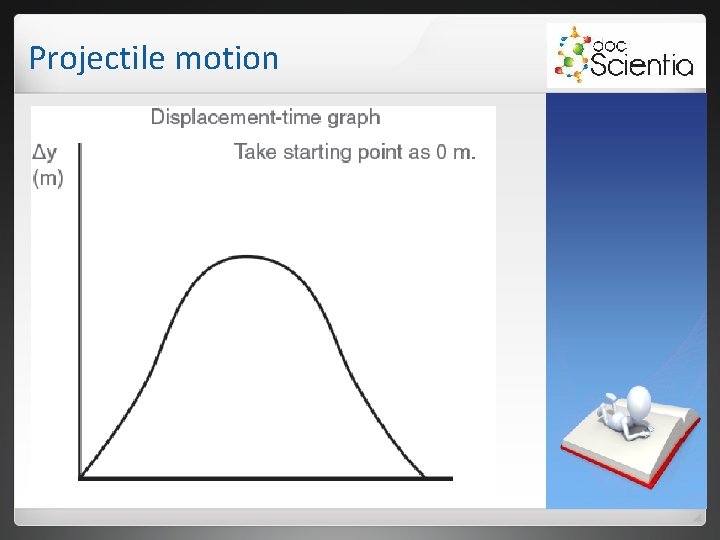
Projectile motion a) Vertically upward (ball returns to starting position).

Projectile motion

Projectile motion

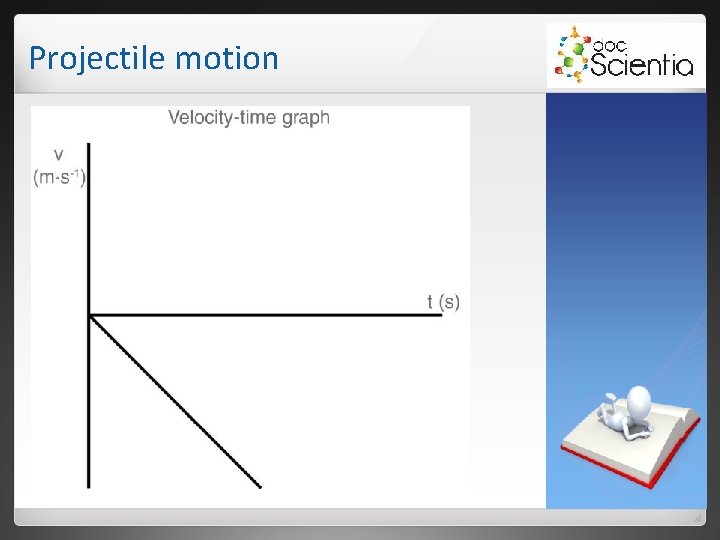
Projectile motion b) Vertically downward (ball is dropped and stops at ground).

Projectile motion

Projectile motion

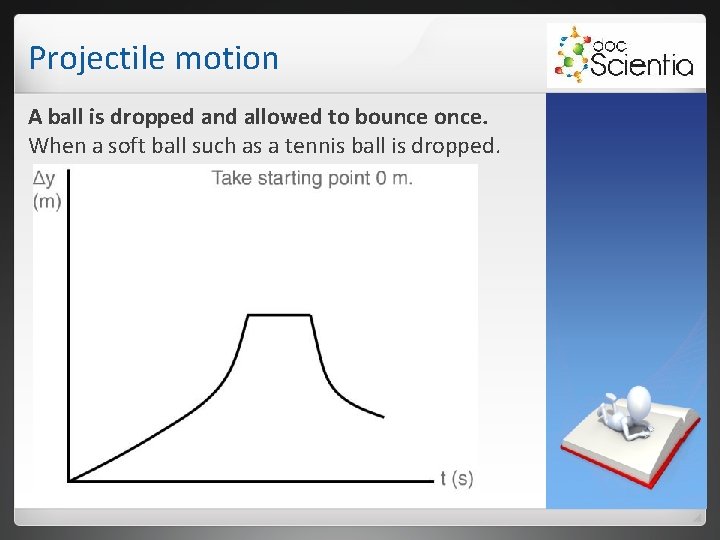
Projectile motion A ball is dropped and allowed to bounce once. When a soft ball such as a tennis ball is dropped.

Projectile motion A ball is dropped and allowed to bounce once. When a soft ball such as a tennis ball is dropped.

Projectile motion A ball is dropped and allowed to bounce once. Wanneer ’n sagte bal, bv. tennisbal, laat val word. The ball changes shape when it hits the contact surface, because it is elastic.

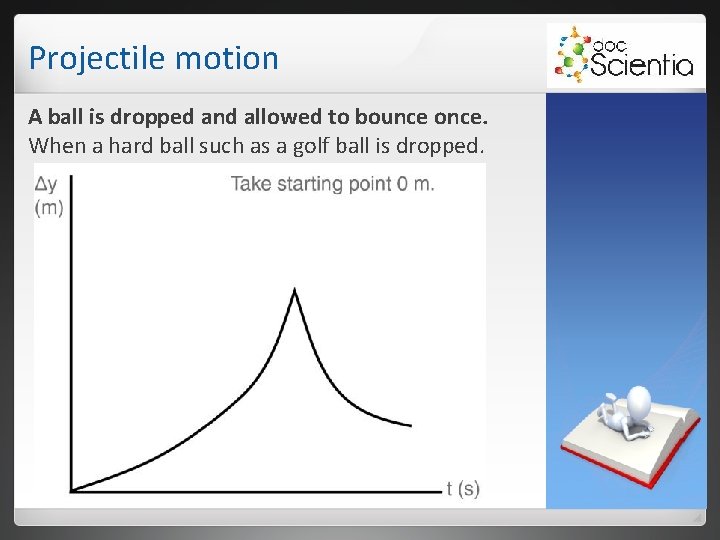
Projectile motion A ball is dropped and allowed to bounce once. When a hard ball such as a golf ball is dropped.

Projectile motion A ball is dropped and allowed to bounce once. When a hard ball such as a golf ball is dropped.

Projectile motion A ball is dropped and allowed to bounce once. When a hard ball such as a golf ball is dropped. The ball does not change shape during contact, because it is rigid.

Projectile motion Examples Morné throws a cricket ball vertically up into the air at a velocity of 20 m⋅s-1. Calculate: 1. the maximum height that the ball reaches; 2. the time it takes for the ball to reach his hand again. This problem has upward and downward motion. For the first question, we are only going to work with the upward motion.

Projectile motion 1. Choose upward + and downward -. At maximum height, the velocity is 0 for an instant, therefore vf = 0 m⋅s-1. The acceleration is 9, 8 m⋅s-2 downwards. The initial velocity is 20 m⋅s-1 upwards. vf 2 = vi 2 + 2 aΔy 0 = (+20)2 + 2(-9, 8)Δy ∴ Δy= +20, 41 m The maximum height is 20, 41 m.

Projectile motion 2. Assume time up = time down. Then we only have to work with upward motion. Choose upward as + and downward as -. vf = vi + aΔt ↑+ 0 = +20 + (-9, 8)Δt Δt = 2, 04 s and the total time = 2 × 2, 04 = 4, 08 s

Projectile motion Another method: If the ball reaches his hand, the displacement is 0 m (the ball ended up where it started). Choose upward as + and downward as -. Δx = viΔt + ½aΔt 2 ↑+ 0 = (+20)t + ½(-9, 8)Δt 2 ∴ 4, 9Δt 2 - 20Δt = 0 ∴ Δt(4, 9Δt - 20) = 0 ∴ Δt = 0 of Δt = 4, 08 s The displacement is 0 m at time 0 s and at time 4, 08 s.

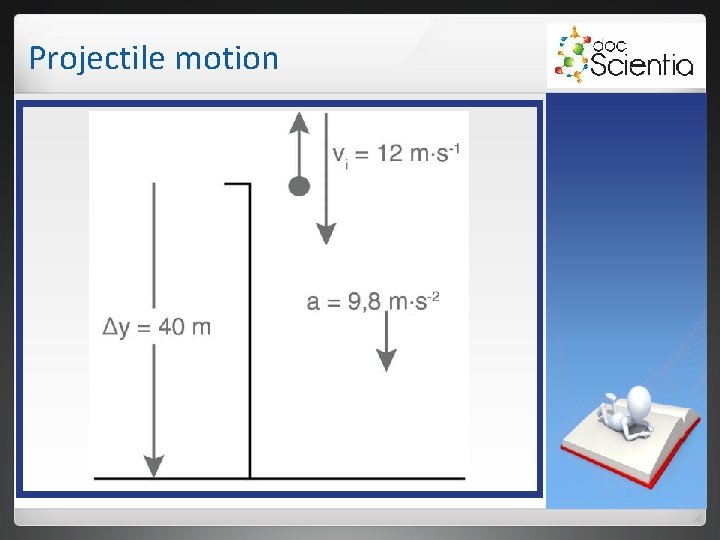
Projectile motion Examples Reneilwe stands on top of a 40 m high building. He leans over the edge and throws a stone vertically upwards at 12 m⋅s-1. The stone lands on the ground next to the building. Calculate: 1. he time taken for the stone to reach the ground. 2. the maximum height from the ground that the stone reaches.

Projectile motion

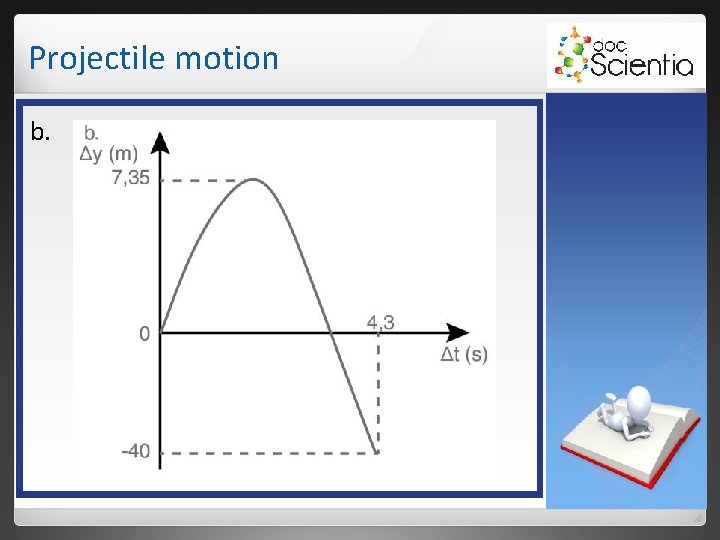
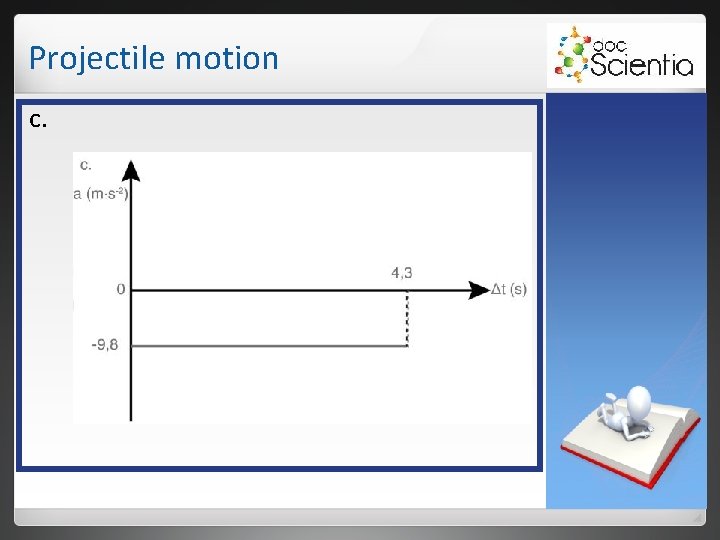
Projectile motion 3. the velocity of the stone as it reaches the ground. 4. Sketch the following free-hand graphs for the total motion: a) velocity-time graph; b) position-time graph; c) acceleration-time graph;

Projectile motion 1. One equation must be used for the upward and downward motions to calculate the time taken for the stone to reach the ground after being thrown upwards. Choose upward as + and downward as -. The total displacement of the stone from the top of the building to the ground is 40 m downwards (from where it started to where it ended).

Projectile motion Δx = viΔt + ½aΔt 2 ↑+ (40 af) = (12 op)Δt + ½(9, 8 af)Δt 2 (-40) = (+12)Δt + ½(-9, 8)Δt 2 4, 9Δt 2 - 12Δt - 40 = 0 Use the formula for solving a quadratic equation. -b ± √ b 2 - 4 ac x = 2 a where a = 4, 9; b = -12 en c = -40 -(-12) ± √(-12)2 - 4(4, 9)(-40) therefore Δt = 2(4, 9) = 4, 33 s (We only use the + of the ± because the other answer will be negative. )

Projectile motion Another method: There is an easier method which is a bit longer, for those who are not comfortable using the quadratic formula. First calculate the final velocity for the applicable motion, then calculate the time using another equation of motion.

Projectile motion vf 2 = vi 2 + 2 a∆x vf 2 = (+12) 2 + 2(-9, 8)(-40) vf 2 = 928 vf = -30, 46 m⋅s-1 vf = vi + a∆t -30, 46 = 12 + (-9, 8)∆t ∆t = 4, 33 s The sign of vf is negative, because it is downwards.

Projectile motion 2. To calculate the maximum height, only the upward motion is considered. The final velocity (at the top) is 0 m⋅s-1, the acceleration remains 9, 8 m⋅s-2 downwards and the initial velocity is 12 m⋅s-1 upwards. vf 2 = vi 2 + 2 aΔy ↑+ 0 = (+12)2 + 2(-9, 8)Δy Δy = 7, 35 m The maximum height above the ground is 40 + 7, 35 = 47, 35 m.

Projectile motion 3. To calculate the velocity with which the stone reaches the ground, the total motion, from the moment the stone was projected upwards to the moment just before it hits the ground, is considered. Any equation of motion can be used because all other values are now known. vi = 12 m⋅s-1 up Total time 4, 3 s. a = 9, 8 m⋅s-2 downwards Displacement = 40 m downwards Final velocity vf is asked. vf = vi + aΔt ↑+ = (+12) + (-9, 8)(4, 3) = -30, 4 dus 30, 4 m⋅s-1 downwards

Projectile motion OR vi = 12 m⋅s-1 op Total time is 4, 3 s. a = 9, 8 m⋅s-2 af Displacement = 40 m downwards Final velocity vf is asked. vf 2 = vi 2 + 2 aΔy ↑+ = (+12)2 + 2(-9, 8)(-40) = ± 30, 4 dus 30, 4 m⋅s-1 downwards

Projectile motion 4 a. Take upward as positive. Take the top of the building as zero displacement.

Projectile motion b.

Projectile motion c.

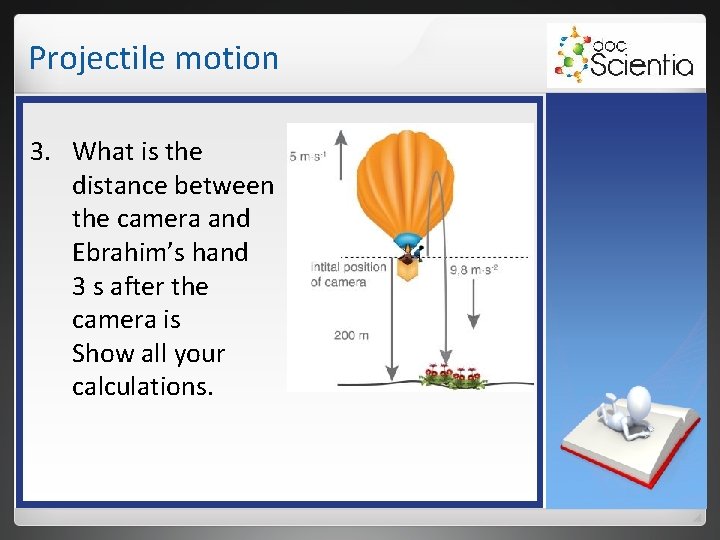
Projectile motion Examples A hot air balloon rises vertically at a constant velocity of 5 m⋅s-1. Ebrahim is standing in the basket of the balloon. He leans over the edge and takes photos with his camera. When the top of the basket is 200 m above the ground, Ebrahim drops his camera. 1. 2. What are the initial velocity and the acceleration of the camera respectively at the moment it is dropped? Calculate the total time it takes for the camera to reach the ground.

Projectile motion 3. What is the distance between the camera and Ebrahim’s hand 3 s after the camera is Show all your calculations. dropped?

Projectile motion It is easier to work from a sketch. Remember that there are two objects in motion. The hot air balloon with a constant upward velocity of 5 m⋅s-1. The camera that moves under the influence of gravitational force only after it is dropped. 1. When the camera leaves Ebrahim’s hand, its gravitational acceleration is 9, 8 m⋅s-2 downwards. It is then a free-falling object. While Ebrahim is holding onto it, it has the same velocity as his hand in the hot air balloon, which is 5 m⋅s-1 upwards. The moment it is released, it also has a velocity of 5 m⋅s-1 upwards.

Projectile motion Quick facts When the camera is dropped, its velocity changes from 5 m⋅s-1 upwards to 0 m⋅s-1 quickly. At the same time, Ebrahim moves with the hot air balloon at a constant velocity of 5 m⋅s-1 upwards. The relative velocity of the camera to Ebrahim is downward, and it seems to Ebrahim as if his camera is moving downwards.

Projectile motion 2. Δx= viΔt + ½aΔt 2 ↑+ (200 af) = (5 op)Δt + ½(9, 8 af)Δt 2 (-200) = (+5)Δt + ½(-9, 8)Δt 2 4, 9Δt 2 - 5Δt - 200 = 0 To solve the equation, use: -b ± √ b 2 - 4 ac x= 2 a where a = 4, 9; b = -5 and c = -200 -(-5) ± √(-5)2 - 4(4, 9)(-200) therefore Δt = 2(4, 9) = 6, 92 s

Projectile motion Another method: vf 2 = vi + 2 aΔy vf 2 = (+5)2 + 2(-9, 8)(-200) vf 2= 3 945 vf= -62, 81 m⋅s-1 vf= vi + a∆t -62, 81 = 5 + (-9, 8)∆t ∆t = 6, 92 s The sign of vf is negative, because the camera is moving downwards.

Projectile motion 3. In 3 s the hot air balloon is moving upwards with a constant velocity of 5 m⋅s-1, therefore its acceleration is 0 m⋅s-2. Δx = viΔt + ½aΔt 2 ↑+ = (+5)(3) + 0 = 15 m above the initial position of the camera The camera first moves upwards then downwards. All with an acceleration of 9, 8 m⋅s-2 downwards.

Projectile motion Δx = viΔt + ½aΔt 2 ↑+ = +5(3) + ½(-9, 8)(3)2 = -29, 1 m This means that the camera is now 29, 1 m below its initial position. Therefore the distance between the camera and Ebrahim’s hand is (15 + 29, 1) = 44, 1 m

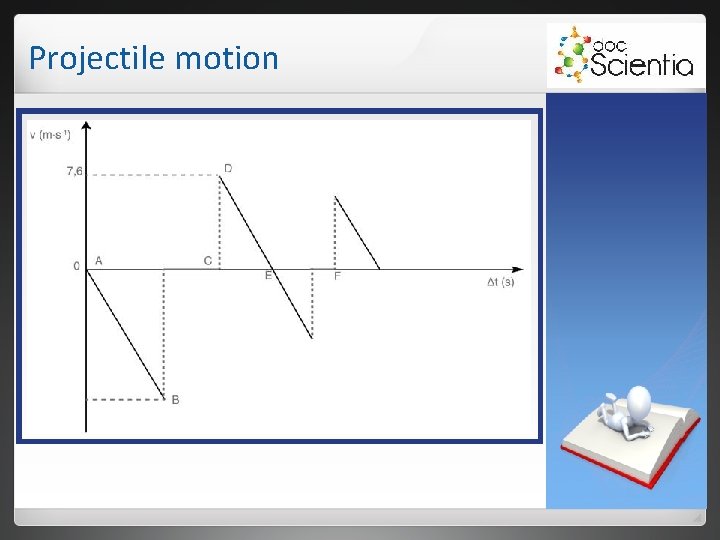
Projectile motion Examples The velocity-time graph describes the motion of a ball, initially at rest, that falls from a height of 5 m. It hits a cement surface and continues to bounce. The graph is labelled A, B, C, D, E and F. Answer the questions that follow.

Projectile motion

Projectile motion 1. 2. 3. 4. 5. 6. Calculate the speed at which the ball reaches the surface. Which letter on the graph corresponds to the moment that the ball hits the surface for the first time? At which letter does the ball reach a maximum height after the first bounce? What happens during interval BD? Why is the magnitude of the velocity smaller at D than at B? What is represented by the gradient of line AB?

Projectile motion 7. Calculate the height that the ball reaches after the first bounce. 8. Draw a displacement-time graph for the motion from A to F. What direction is positive in this example? Upward or downward? If we look at AB on the graph, it represents the downward velocity of the ball while it falls, and is negative. Upward is therefore positive. .

Projectile motion 1. 2. 3. vi = 0 m⋅s-1, a = 9, 8 m⋅s-2 downwards, Δy = 5 m downwards and vf must be calculated. vf 2 = vi 2 + 2 aΔy ↑+ = 0 + 2(-9, 8)(-5) ∴ vf = ± √ 98 = -9, 9 m⋅s-1 B; die tydperk tussen B en D is die tyd wat die bal in kontak is met die blad. Dit is dan die tydperk waarin die impuls plaasvind wat die blad en die bal op mekaar uitoefen. E; die snelheid is vir ’n oomblik 0 m⋅s-1.

Projectile motion 4. The ball is in contact with the surface, and in a very short time the velocity of the ball changes from 9, 9 m⋅s-1 to 0 m⋅s-1. Then it increases up to the point when it leaves the surface with a velocity of 7, 6 m⋅s-1 upwards. 5. During the collision with the surface, some of the kinetic energy of the ball is converted into other forms of energy, such as sound, heat, etc. The collision is therefore elastic and it is not a closed/isolated system.

Projectile motion 6. Acceleration; in this case, gravitational acceleration, g = 9, 8 m⋅s-2 downwards (take note that the gradient is negative). 7. The initial velocity of the ball is now vi = 7, 6 m⋅s-1 upwards, the final velocity at maximum height is vf = 0 m⋅s-1 and the acceleration again is a = 9, 8 m⋅s-2 downwards. vf 2 = vi 2 + 2 aΔy ↑+ 0 = (+7, 6)2 + 2(-9, 8)Δy Δy = 2, 95 m upwards

Projectile motion 8. The initial position is 5 m above the surface, therefore +5 and the ball hits the surface where the position is 0 m (if we consider the surface to be the zero position).

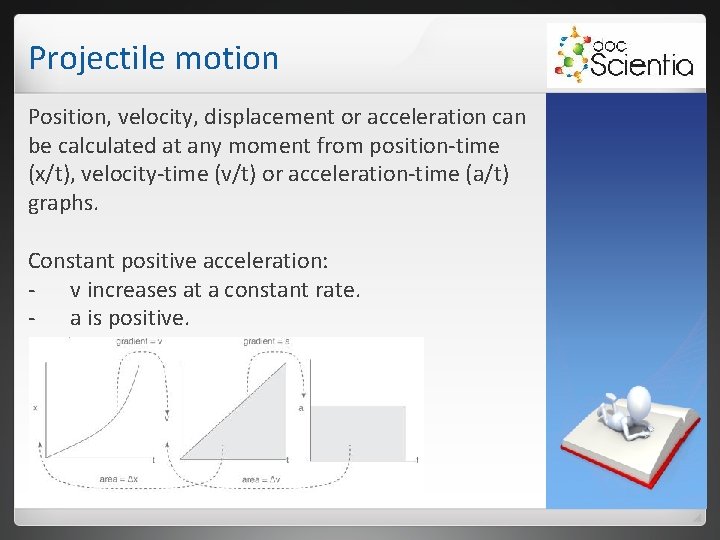
Projectile motion Position, velocity, displacement or acceleration can be calculated at any moment from position-time (x/t), velocity-time (v/t) or acceleration-time (a/t) graphs. Constant positive acceleration: - v increases at a constant rate. - a is positive.

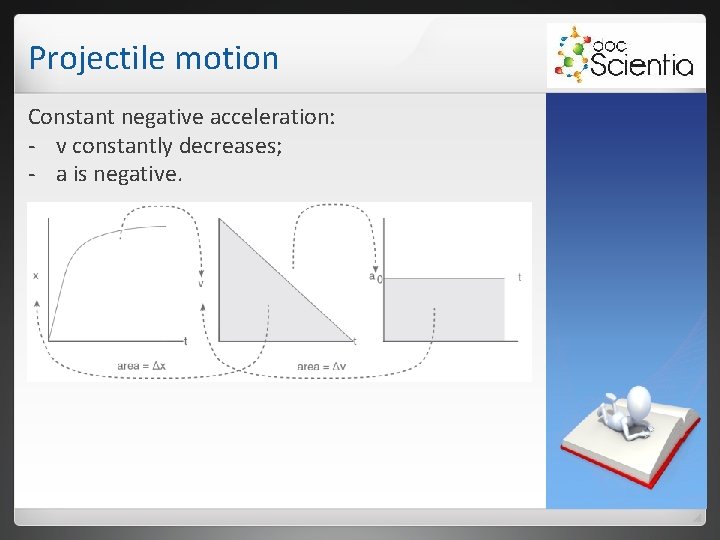
Projectile motion Constant negative acceleration: - v constantly decreases; - a is negative.

Projectile motion To calculate the gradient: Δy-axis gradient = Δx-axis To calculate area:

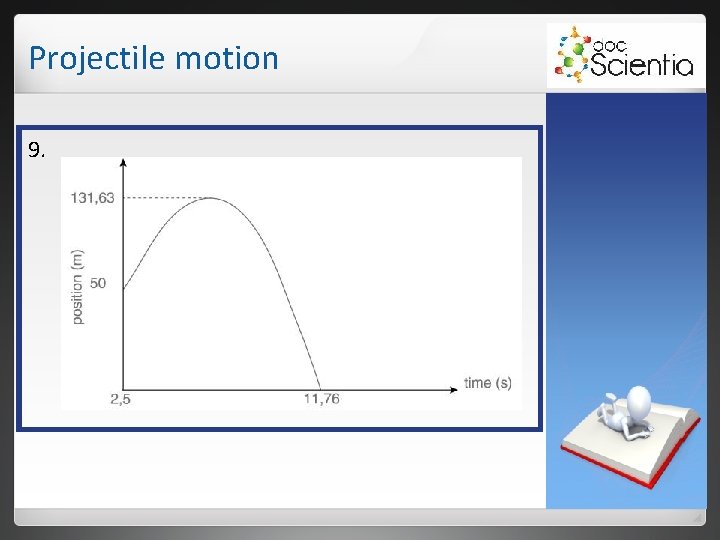
Projectile motion Examples A rocket accelerates uniformly, vertically upwards from rest, and reaches a height of 50 m in the first 2, 5 s of upward motion. The following velocity-time graph shows the motion of the rocket;

Projectile motion The graph describes the motion from the moment the rocket starts to accelerate from rest to the time that it reaches the ground again. After 2, 5 s, the engines cut out and there is no more thrust for the rocket. 1. 2. 3. 4. Calculate the magnitude of the rocket’s acceleration during the first 2, 5 s. Describe the motion of the rocket from the moment that the engines cut out. What is the acceleration of the rocket after the first 2, 5 s? Calculate the velocity v 1 of the rocket at 2, 5 s.

Projectile motion 5. 6. 7. 8. 9. Where will the rocket be on its trajectory at time �� ? Calculate the height above the ground at time ��. Show, by calculation, that the time y, at which the rocket reaches the ground, is 11, 76 s. Calculate the velocity at which the rocket reaches the ground. Draw a position-time graph from 2, 5 s. Show all calculated intercept values on the axes. Use the ground as zero position.

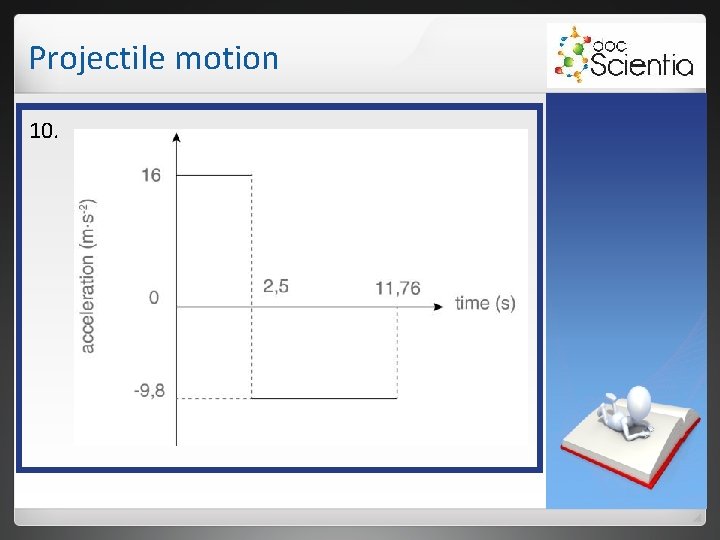
Projectile motion 10. Draw an acceleration-time graph for the total motion (from the moment the rocket is launched). Show all calculated values on the axes. 1. Δy = viΔt + ½aΔt 2 50 = 0 + ½a(2, 5)2 a = 16 m⋅s-2 upwards Δy = 50 m vi = 0 m⋅s-1 Δt = 2, 5 s (Use upward as +. )

Projectile motion 2. The rocket continues to move upwards with a decreasing velocity until it becomes zero for a moment at maximum height. During this time, the acceleration is 9, 8 m⋅s-2 downwards. Then it moves downwards and accelerates at 9, 8 m⋅s-2 downwards. 3. 9, 8 m⋅s-2 downwards

Projectile motion 4. This question can be answered in two ways: Method 1: The area between the graph and the time-axis gives displacement: ½ × b × h = displacement ½(2, 5)v 1 = 50 v 1 = 40 m⋅s-1 upwards Method 2: Use an equation of motion for the first 2, 5 seconds. vf = vi + aΔt v 1 = 0 + (16 × 2, 5) = 40 m⋅s-1 upwards

Projectile motion 5. At maximum height, its velocity is zero for a moment. 6. Use an equation of motion from time = 2, 5 s to time x. Remember that gravitational acceleration is now used. vi = 40 m⋅s-1 up (+) vf 2 = vi 2 + 2 aΔy vf = 0 m⋅s-1 0 = +402 - (2 × 9, 8Δy) a = 9, 8 m⋅s-2 down (-) Δy = 81, 63 m Its maximum height above the ground is therefore 50 m + 81, 63 m = 131, 63 m.

Projectile motion 7. Choose upward as positive to calculate the time taken to reach the ground after the first 2, 5 s. Remember that the rocket will end up 50 m lower than it was at 2, 5 s. Δx = viΔt + ½aΔt 2 -50 = 40Δt + ½(-9, 8)Δt 2 4, 9Δt 2 - 40Δt(-50) = 0 Δx = 50 m down, therefore -50 a = 9, 8 m⋅s-2 down, therefore -9, 8 vi = 40 m⋅s-2 upwards, therefore +40

Projectile motion Now use the formula: -b ± √ b 2 - 4 ac x = 2 a where a = 4, 9; b = -40 en c = -50 -(-40) ± √(-40)2 - 4(4, 9)(-50) therefore Δt = 2(4, 9) = 9, 26 s But the first 2, 5 s must still be added, therefore the total time is 11, 76 s.

Projectile motion Quick facts The negative answer is not used, because time cannot be negative.

Projectile motion Nog ’n metode: vf 2 = vi 2 + 2 aΔy vf 2 = (+40) 2 + 2(-9, 8)(-50) vf 2 = 2 580 vf = -50, 59 m⋅s-1 vf = vi + a∆t -50, 59 = 40 + (-9, 8)∆t ∆t = 9, 26 s vf is negative, because it is downward. But the first 2, 5 s must still be added, therefore the total time is 11, 76 s.

Projectile motion 8. To calculate the final velocity we work from 2, 5 s to the end. Therefore with a time of 9, 26 s. vf = vi + aΔt vf = +40 - 9, 8(9, 26) = -50, 75 m⋅s-1 = 50, 75 m⋅s-1 downwards vf = must be calculated vi = 40 m⋅s-1 upwards (+40) a = 9, 8 m⋅s-2 af (-9, 8)

Projectile motion NB: Take note that the acceleration of the rocket after 2, 5 s differs from before. An equation of motion can only be used if the acceleration is constant. Separate calculations must be done for the first 2, 5 s and the time thereafter.

Projectile motion 9.

Projectile motion 10.

Projectile motion For the first 2, 5 s: a = gradient of graph Δv a = Δt 40 - 0 a = 2, 5 - 0 a = 16 m⋅s-2

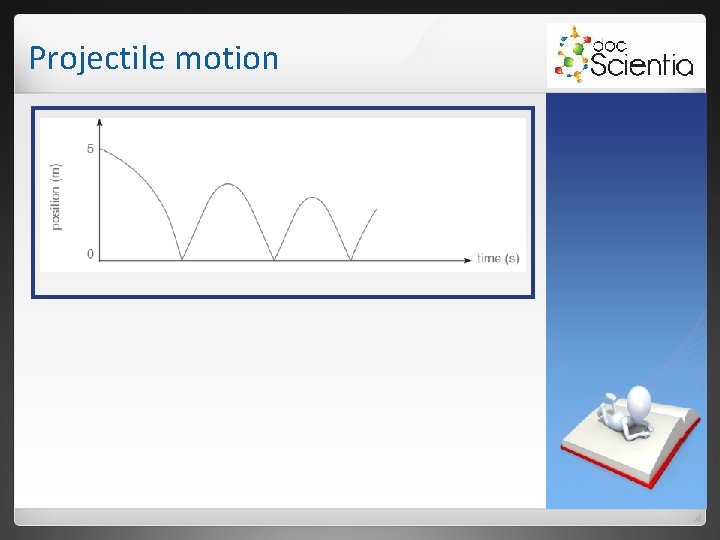
Projectile motion Examples Sijabulile drops a ball, mass 150 g, from a height of 5 m. The ball reaches the ground with a downward velocity of 9 m⋅s-1 and bounces back up at 7 m⋅s-1. The ball bounces twice more before Sijabulile catches it. Assume that the time of contact between the ball and the ground is so small that it does not need to be indicated.

Projectile motion 1. Draw a position-time graph for the motion until just after the last bounce. Show the initial position of the ball. 2. Draw the velocity-time graph for the same motion. Show the velocities -9 m⋅s-1 and 7 m⋅s 1, as mentioned above, on your graph.

Projectile motion 1. Choose upward as positive. Note the following: • The ball starts at a height of 5 m. • The height that it reaches after each bounce, decreases. • The equation for position over time is: Δx = viΔt + ½aΔt 2. • It is therefore an equation in the form of y = ax 2 + bx + c and is therefore a parabola. • For the parabola, the gravitational acceleration is - since upward is +, and it is a negative parabola.

Projectile motion

Projectile motion 2. Choose upward as positive again. Take note of the following: • The initial velocity of the ball is zero. • It is moving downwards (-) with a velocity of increasing magnitude. • When it reaches the ground (A), its velocity is 9 m⋅s-1 downwards, thus -9. • The ball must now leave the ground with a velocity of 7 m⋅s-1 upwards (B), that is why the graph “jumps” up to +7.

Projectile motion • Now the ball moves upwards (+) with decreasing velocity until it reaches its highest point (C), where its velocity is zero for a moment. • The ball now drops (-) and hits the ground (D) with a smaller speed than the first time. • It continues this way until the ball is caught.

Projectile motion • It is very important that the gradients of the graph are equal. The gradient gives the acceleration which is 9, 8 m⋅s-2 downwards for the time that the ball is not in contact with the ground. • gradient = acceleration Acceleration of the ball while it is not making contact with the surface is always 9, 8 m⋅s-2 downwards.

Projectile motion