Grade 12 AP Calculus MCV 4 UE Chapter

Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All

Why Linearization? Real systems are inherently nonlinear. (Linear systems do not exist!) Ex. f(t)=Kx(t),

Example 1: Finding a Linearization and Newton’s Method © 2020 E. Choi – MCV

Linearization can never replace a calculator when it comes to find square roots.

Example 2: Finding a Linearization and Newton’s Method © 2020 E. Choi – MCV

c) i) ii) Notice that if k is a positive integer binomial theorem.

Example 4: Approximation Roots Use linearization to approximate a) b) Since the closest perfect

Example 4: Approximation Roots Use linearization to approximate a) b) Since the closest cubic

A quartic equation and higher…. (No formula developed yet!) Do you want to memorize

Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE -

Example 7: Finding the Differential dy Find the differential dy and evaluate dy for

Example 8: Finding Differentials of Functions Find the differentials of the followings Linearization and

Tolerance is a permissible differences, allowing some freedom to move within limits. Linearization and

GTA: 2751 square mile (About 3. 6 GTA) Richmond Hill: 39 square mile

Homework Textbook: P. 242 #1 -7, 9 -13, 19 -33, 37 -40, 46 -54

End of lesson Linearization and Newton’s Method © 2020 E. Choi – MCV 4

Slides: 23

Download presentation

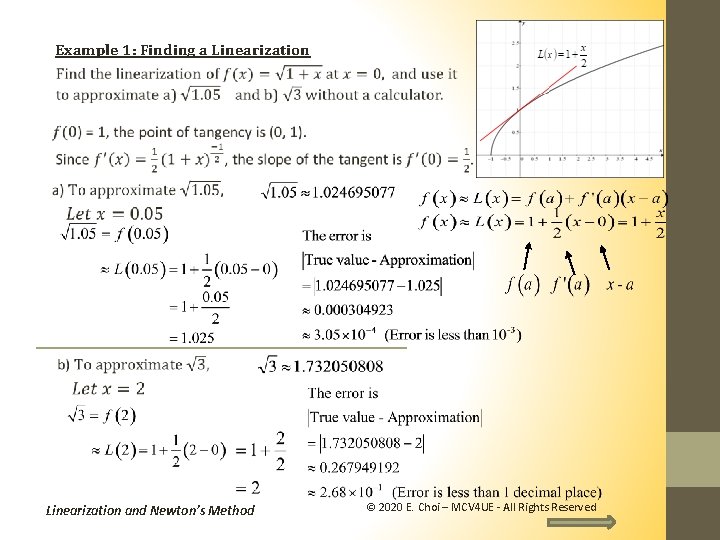
Why Linearization? Real systems are inherently nonlinear. (Linear systems do not exist!) Ex. f(t)=Kx(t), v(t)=Ri(t) Nonlinear systems are difficult to deal with mathematically. Many control analysis/design techniques are available for linear systems. Linear approximation is often good enough for control system analysis and design purposes. Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All Rights Reserved

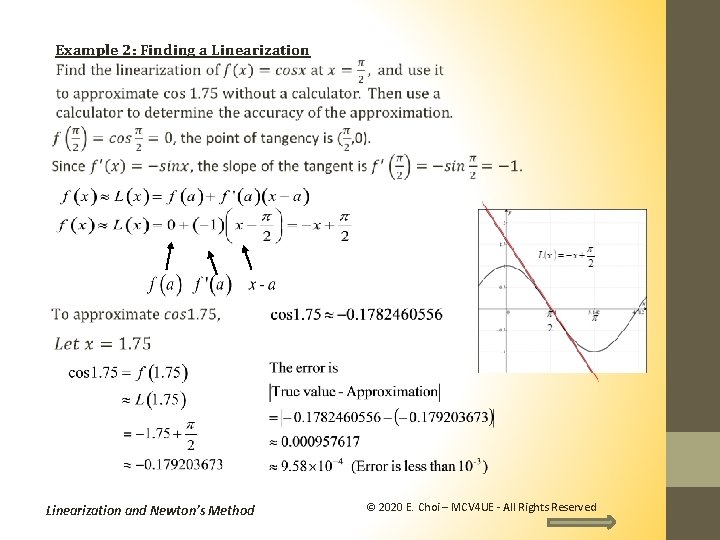
Linearization can never replace a calculator when it comes to find square roots. As we move away from zero (the center of the approximation), we lose accuracy and the approximation becomes less useful. Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All Rights Reserved

c) i) ii) Notice that if k is a positive integer binomial theorem. But the formula actually holds for all real values of k. Linearization and Newton’s Method iii) © 2020 E. Choi – MCV 4 UE - All Rights Reserved

Example 4: Approximation Roots Use linearization to approximate a) b) Since the closest perfect square to 147 is 144, so we center the linearization at x = 144. The tangent line at (144, 12) has slope. Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All Rights Reserved

Example 4: Approximation Roots Use linearization to approximate a) b) Since the closest cubic root to 201 is 216, so we center the linearization at x = 216. The tangent line at (216, 6) has slope. Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All Rights Reserved

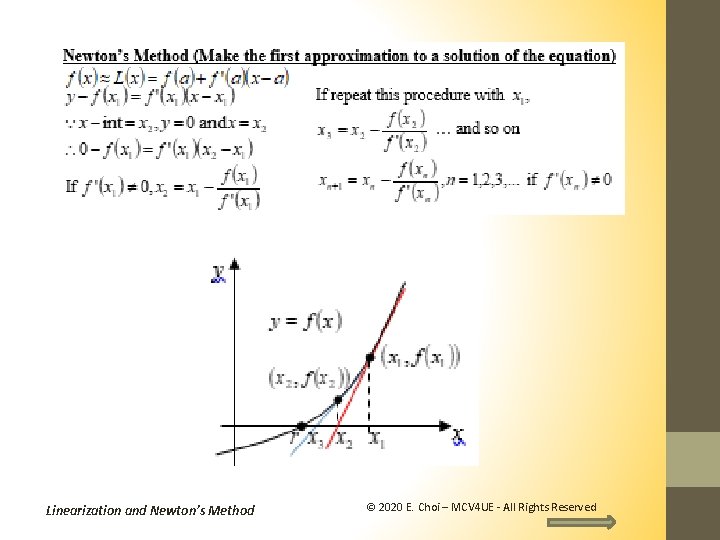
A quartic equation and higher…. (No formula developed yet!) Do you want to memorize the Cardano’s formula? (Feel free to and also feel free to find the proof of it!) How about for the equations of higher degrees? Using Newton’s Method, we can find approximations to the solutions of such equations. Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All Rights Reserved

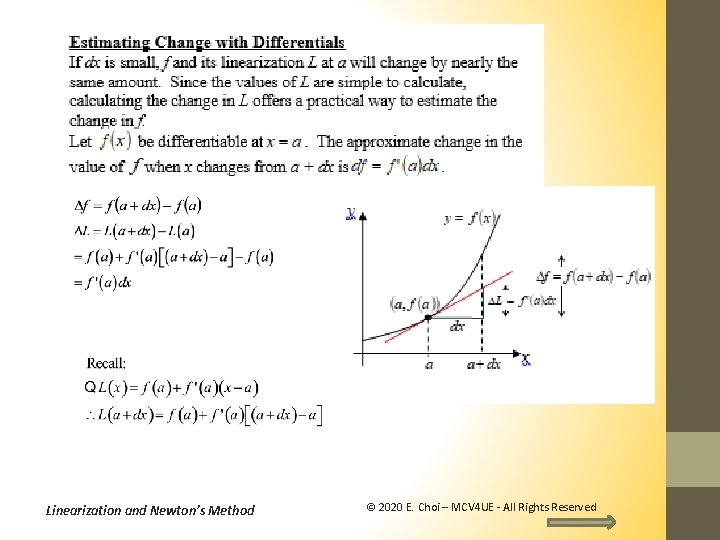
Example 7: Finding the Differential dy Find the differential dy and evaluate dy for the given values of x and dx. How is this related to Linearization? Think about it as Change of y when Change of x is _______. See explains after example 8. Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All Rights Reserved

GTA: 2751 square mile (About 3. 6 GTA) Richmond Hill: 39 square mile (About 255 Richmond Hill) Therefore the effect of the tolerance is approx. . 9950 square mile. (25770 km 2) Linearization and Newton’s Method © 2020 E. Choi – MCV 4 UE - All Rights Reserved