Grade 12 Advanced Functions MHF 4 U Unit











- Slides: 12

Grade 12 Advanced Functions (MHF 4 U) Unit 1: Polynomial Functions Symmetry Mr. Choi © 2017 E. Choi – MHF 4 U - All Rights Reserved

Symmetry To determine the symmetry, replace –x with x in the relation, then determine the symmetry according to the following. Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Symmetry For Polynomial functions, An even-degree polynomial function is an even function if the exponent of each term is even. An odd-degree polynomial function is an odd function if the exponent of each term is odd. Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Example 1 Determine whether the function is even, odd, or neither. Check the symmetries from the screen captures. a) Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Example 1 Determine whether the function is even, odd, or neither. Check the symmetries from the screen captures. b) Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Example 1 Determine whether the function is even, odd, or neither. Check the symmetries from the screen captures. c) Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

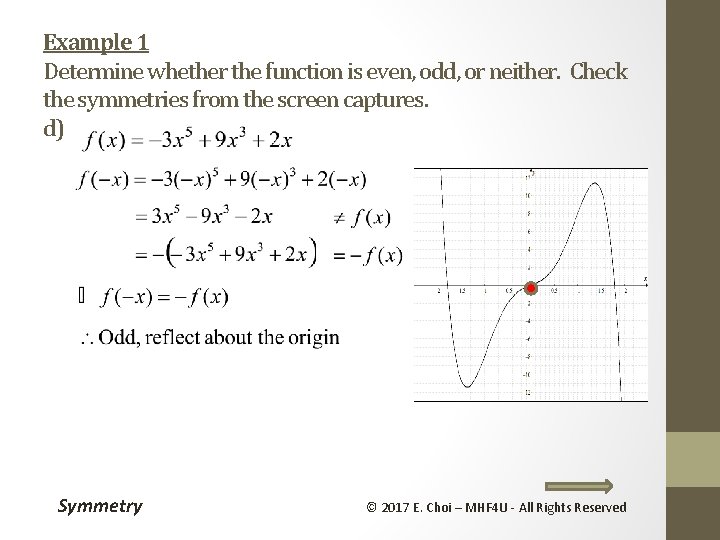
Example 1 Determine whether the function is even, odd, or neither. Check the symmetries from the screen captures. d) Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Example 1 Determine whether the function is even, odd, or neither. e) Since it is a polynomial with the exponent of each term is even, therefore it is an even function. Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Example 1 Determine whether the function is even, odd, or neither. f) Since it is a polynomial with some exponents in it are even and some are odd, therefore it is a neither function. Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Example 1 Determine whether the function is even, odd, or neither. g) Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

Homework • P. 39 #3 -5, 7, 8, 12, 14 • Worksheet: Symmetry Check the website for updates Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved

End of lesson Symmetry © 2017 E. Choi – MHF 4 U - All Rights Reserved