Grade 11 System of forces Understanding forces Before

Grade 11 System of forces

Understanding forces • Before attempting calculating system of forces, you first need to understand a few basics: Mechanical Technology Curriculum Coordination & Support

Cartesian Plane • Vertical axis = Y axis _ + Mechanical Technology Curriculum Coordination & Support

Cartesian Plane • Horizontal axis = X axis + _ Mechanical Technology Curriculum Coordination & Support

Cartesian Plane Y X X Y Mechanical Technology Curriculum Coordination & Support

Cartesian Plane 90° NOTE THE DIRECTION OF ROTATION 0° 360° 180° ANTI-CLOCKWISE START AT 0° 270° Mechanical Technology Curriculum Coordination & Support

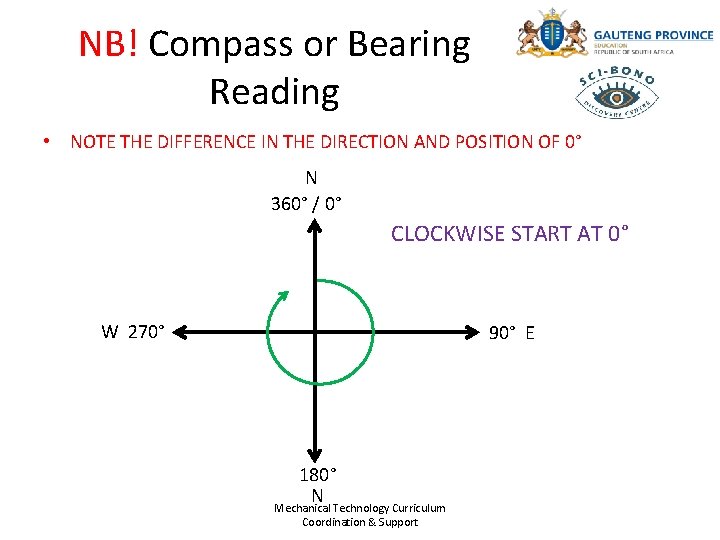
NB! Compass or Bearing Reading • NOTE THE DIFFERENCE IN THE DIRECTION AND POSITION OF 0° N 360° / 0° CLOCKWISE START AT 0° W 270° 90° E 180° N Mechanical Technology Curriculum Coordination & Support

Understanding forces • It is important to understand the difference between the Cartesian plane and the Compass • It will help understand when calculating the direction of the resultant Mechanical Technology Curriculum Coordination & Support

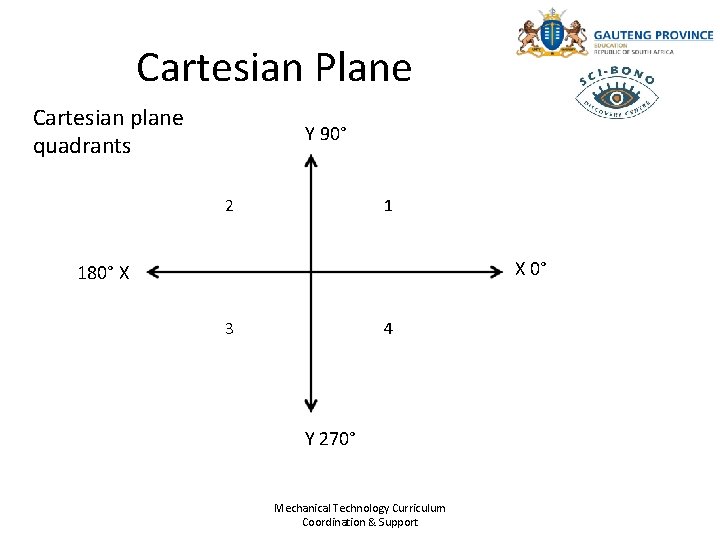
Cartesian Plane Cartesian plane quadrants Y 90° 2 1 X 0° 180° X 3 4 Y 270° Mechanical Technology Curriculum Coordination & Support

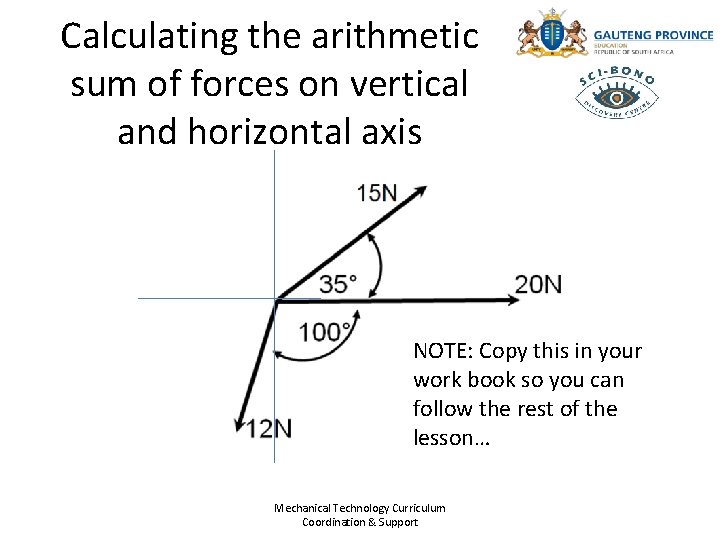
Calculating the arithmetic sum of forces on vertical and horizontal axis NOTE: Copy this in your work book so you can follow the rest of the lesson… Mechanical Technology Curriculum Coordination & Support

Step 1 • Draw a table with the following headings… Force Vertical Component (Y) Horizontal Component (X) Mechanical Technology Curriculum Coordination & Support

Step 2 • Write in the relevant forces… Force Vertical Component (Y) Horizontal Component (X) 20 N 15 N 12 N Mechanical Technology Curriculum Coordination & Support

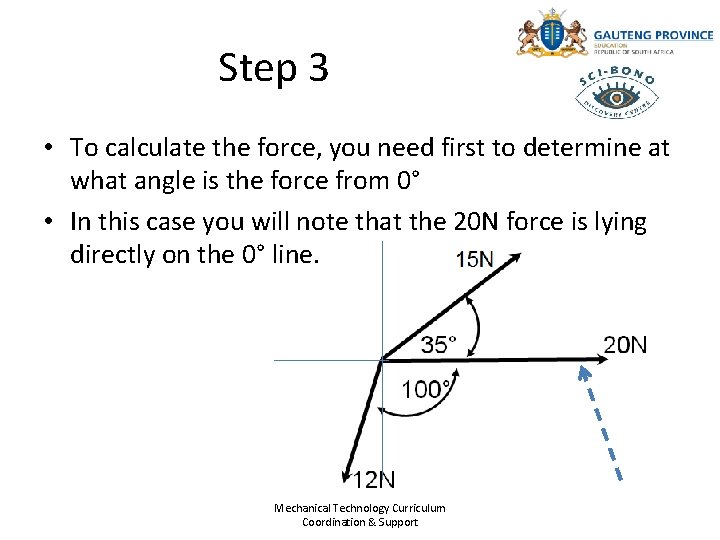
Step 3 • To calculate the force, you need first to determine at what angle is the force from 0° • In this case you will note that the 20 N force is lying directly on the 0° line. Mechanical Technology Curriculum Coordination & Support

Step 3 • You need to use Sin to calculate the vertical components…therefor it is the force (20 N) x Sinɵ Force 20 N Vertical Component (Y) 20 Sin 0° Horizontal Component (X) 0 N 15 N 12 N NB!! Do not forget the units in your answer!! Mechanical Technology Curriculum Coordination & Support

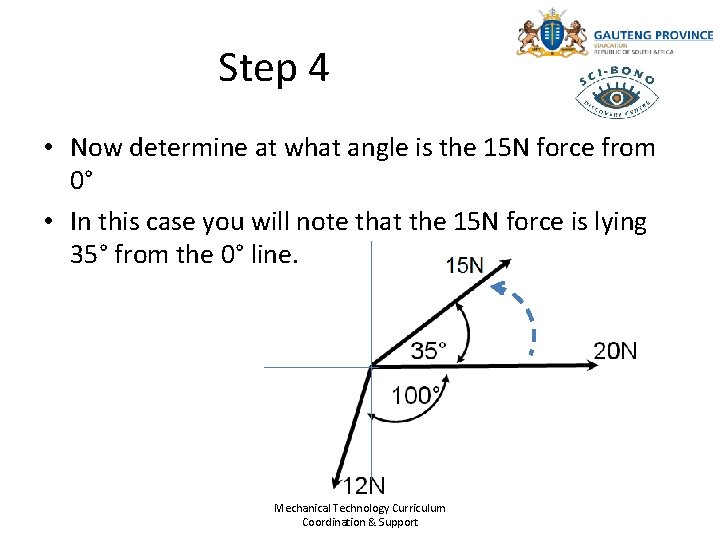
Step 4 • Now determine at what angle is the 15 N force from 0° • In this case you will note that the 15 N force is lying 35° from the 0° line. Mechanical Technology Curriculum Coordination & Support

Step 4 • You need to use Sin to calculate the vertical components…therefor it is the force (15 N) x Sinɵ Force Vertical Component (Y) 20 N 20 Sin 0° 0 N 15 Sin 35° 8, 60 N Horizontal Component (X) 12 N Mechanical Technology Curriculum Coordination & Support

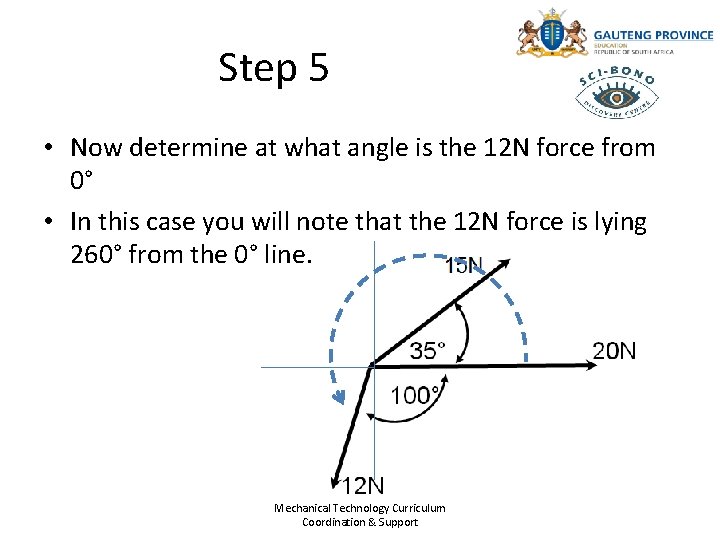
Step 5 • Now determine at what angle is the 12 N force from 0° • In this case you will note that the 12 N force is lying 260° from the 0° line. Mechanical Technology Curriculum Coordination & Support

Step 5 • You need to use Sin to calculate the vertical components…therefor it is the force (12 N) x Sinɵ Force Vertical Component (Y) 20 N 20 Sin 0° 0 N 15 Sin 35° 8, 60 N 12 Sin 260° -11, 82 N Horizontal Component (X) Note the (minus) sign – do not forget it! Mechanical Technology Curriculum Coordination & Support

Step 6 • Now you add up all the forces to get to the arithmetic sum of the vertical forces Force Vertical Component (Y) 20 N 20 Sin 0° 0 N 15 Sin 35° 8, 60 N 12 Sin 260° -11, 82 N Horizontal Component (X) -3, 22 N Mechanical Technology Curriculum Coordination & Support

Horizontal components • Now to calculate the horizontal components, you repeat the steps as for the vertical components and instead of Sin, you must now use Cosɵ for the horizontal components. Mechanical Technology Curriculum Coordination & Support

Step 7 • Now calculate all the horizontal forces to get to the arithmetic sum of the horizontal forces Force Vertical Component (Y) Horizontal Component (X) 20 N 20 Sin 0° 0 N 20 Cos 0° 20 N 15 Sin 35° 8, 60 N 15 Cos 35° 12, 29 N 12 Sin 260° -11, 82 N 12 Cos 260° -2, 08 N -3, 22 N Mechanical Technology Curriculum Coordination & Support 10, 21 N

Pushing forces • To calculate the vertical and horizontal components of forces, you can not work with any pushing forces (Remember parallelogram forces in grade 10? ) • You first need to convert the pushing force into a pulling force before calculating anything! Mechanical Technology Curriculum Coordination & Support

Pushing Force Mechanical Technology Curriculum Coordination & Support

Pushing force converted into a pulling force Mechanical Technology Curriculum Coordination & Support

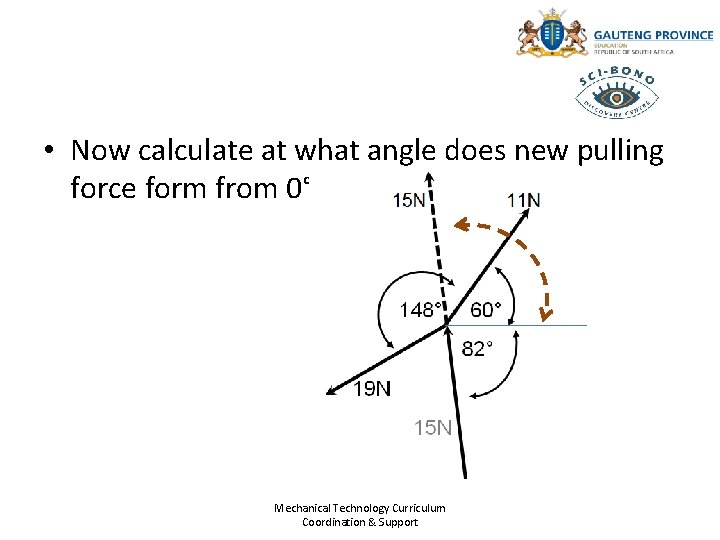
• Now calculate at what angle does new pulling force form from 0° Mechanical Technology Curriculum Coordination & Support

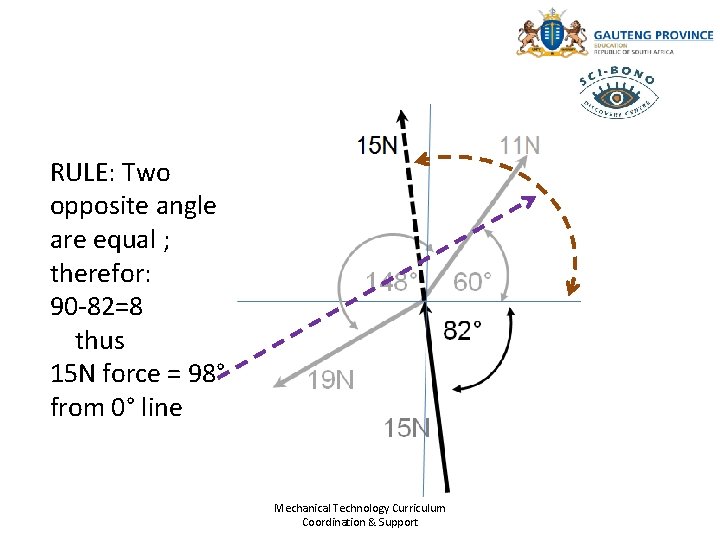
RULE: Two opposite angle are equal ; therefor: 90 -82=8 thus 15 N force = 98° from 0° line Mechanical Technology Curriculum Coordination & Support

Calculating the Resultant • To calculate the Resultant of the system of forces , we are using Pythagoras • Pythagoras theorem - a² = b² + c² c² a² b² Mechanical Technology Curriculum Coordination & Support

Calculating the Resultant • To calculate the Resultant of the system of forces , we are using Pythagoras • Now we can use the same theorem R² = x² + y² R² y² x² Mechanical Technology Curriculum Coordination & Support

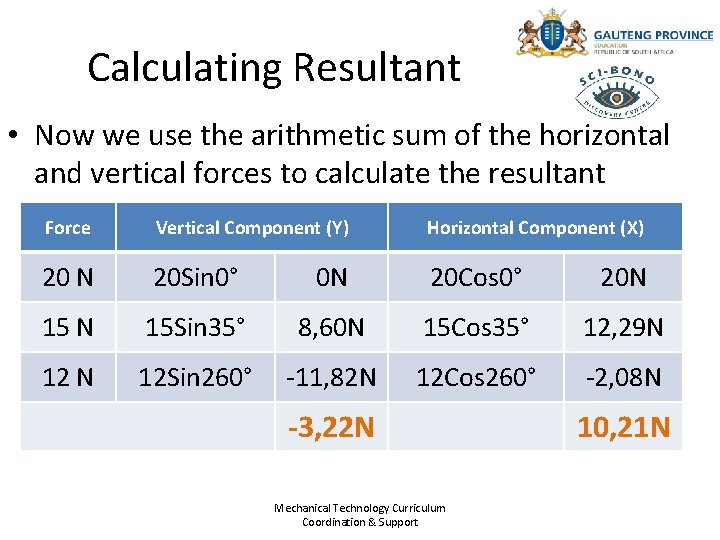
Calculating Resultant • Now we use the arithmetic sum of the horizontal and vertical forces to calculate the resultant Force Vertical Component (Y) Horizontal Component (X) 20 N 20 Sin 0° 0 N 20 Cos 0° 20 N 15 Sin 35° 8, 60 N 15 Cos 35° 12, 29 N 12 Sin 260° -11, 82 N 12 Cos 260° -2, 08 N -3, 22 N Mechanical Technology Curriculum Coordination & Support 10, 21 N

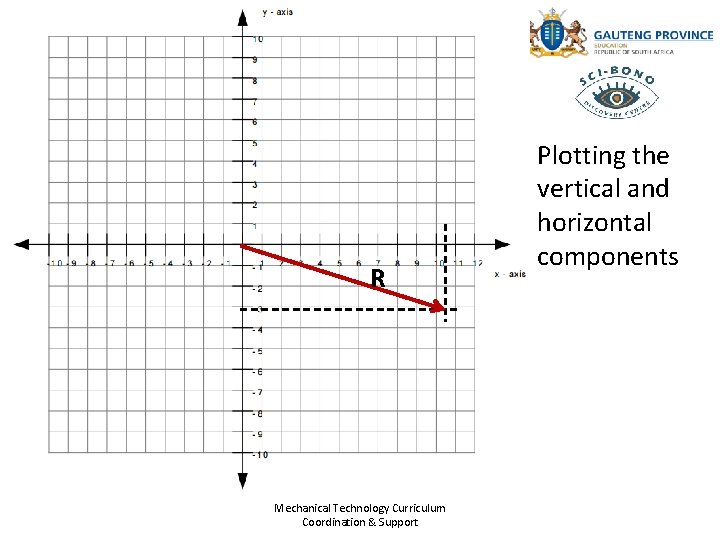
R Mechanical Technology Curriculum Coordination & Support Plotting the vertical and horizontal components

Calculate the Resultant • Mechanical Technology Curriculum Coordination & Support

Direction • Therefor the Resultant is 10, 71 N South from East (Remember your Compass bearings!) N W E S Mechanical Technology Curriculum Coordination & Support

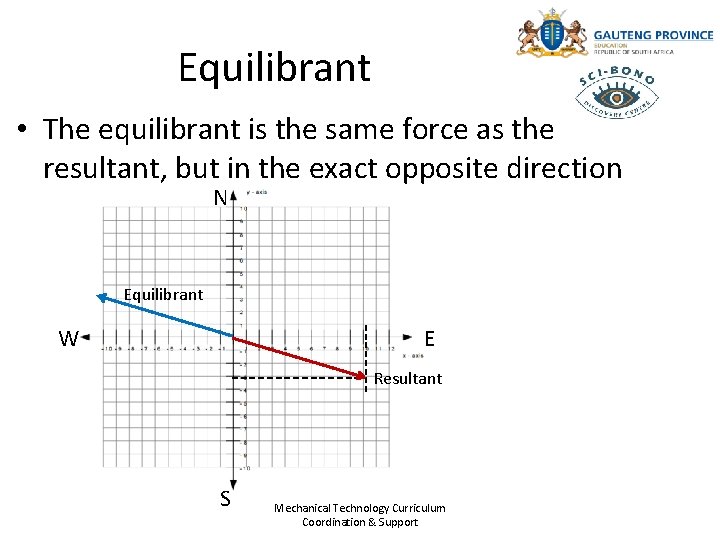
Equilibrant • The equilibrant is the same force as the resultant, but in the exact opposite direction N Equilibrant W E Resultant S Mechanical Technology Curriculum Coordination & Support