Grade 10 Academic MPM 2 D Unit 4

Quadratic Relations • The expression defines a quadratic relation in vertex form. • The

Quadratic Relations (Vertex Form) The expression defines a quadratic relation called the vertex form

Summary (Translations) Quadratic Relations (Translations) y = (x - p)2 p>0 p<0 Descriptions /

Summary (Opening and Stretches) Quadratic Relations (Vertical Stretches) y = ax 2 Descriptions /

Example 1: Parabola with Transformations Find the vertex, the axis of symmetry, the direction

Example 2: Parabola with Transformations Determine a quadratic relation in vertex form which contains

Homework Work sheet: Day 1: Quadratic Relations in Vertex Form (Transformations) Day 2: Graphing

End of lesson Quadratic Relations (Vertex Form): Transformations © 2017 E. Choi – MPM

Slides: 14

Download presentation

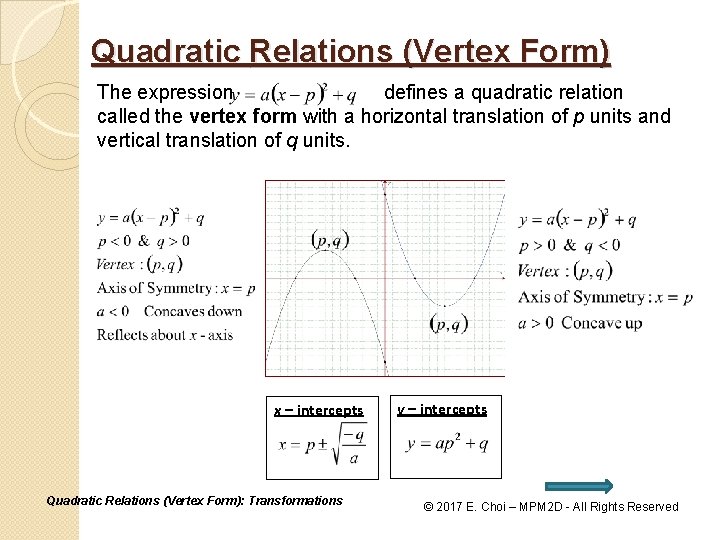
Quadratic Relations • The expression defines a quadratic relation in vertex form. • The coordinates of the vertex of the corresponding parabola are (p, q). • If a > 0, the parabola opens upward. If a < 0, the parabola opens downward. • A quadratic relation in vertex form can be converted to standard form by expanding and collecting like terms. • A quadratic relation in standard form can be converted to vertex form by completing the squares which will be discussed in this unit. Quadratic Relations (Vertex Form): Transformations © 2017 E. Choi – MPM 2 D - All Rights Reserved

Quadratic Relations (Vertex Form) The expression defines a quadratic relation called the vertex form with a horizontal translation of p units and vertical translation of q units. x – intercepts Quadratic Relations (Vertex Form): Transformations y – intercepts © 2017 E. Choi – MPM 2 D - All Rights Reserved

Summary (Translations) Quadratic Relations (Translations) y = (x - p)2 p>0 p<0 Descriptions / Mapping Rules (x, y) (x + p, Translates p units y) Right Translates p units Left (x, y) (x - p, y) y = x 2 + q Descriptions / Mapping Rules q>0 Translates q units Up (x, y) (x, y + q<0 Examples Translates q units Down Quadratic Relations (Vertex Form): Transformations Examples q) (x, y) (x, y - q) © 2017 E. Choi – MPM 2 D - All Rights Reserved

Summary (Opening and Stretches) Quadratic Relations (Vertical Stretches) y = ax 2 Descriptions / Mapping Rules Examples a>1 Vertically expand by a factor of a (x, y) (x, ay) a y) (x, ay) 0 < a < 1 Vertically compress by a factor of (x, Quadratic Relations (Opening) y = ax 2 Descriptions / Mapping Rules a>0 Opens (Concaves) up (x, y) (x, +ay) a<0 Opens (Concaves) down (x, y) (x, -ay) Quadratic Relations (Vertex Form): Transformations Examples © 2017 E. Choi – MPM 2 D - All Rights Reserved

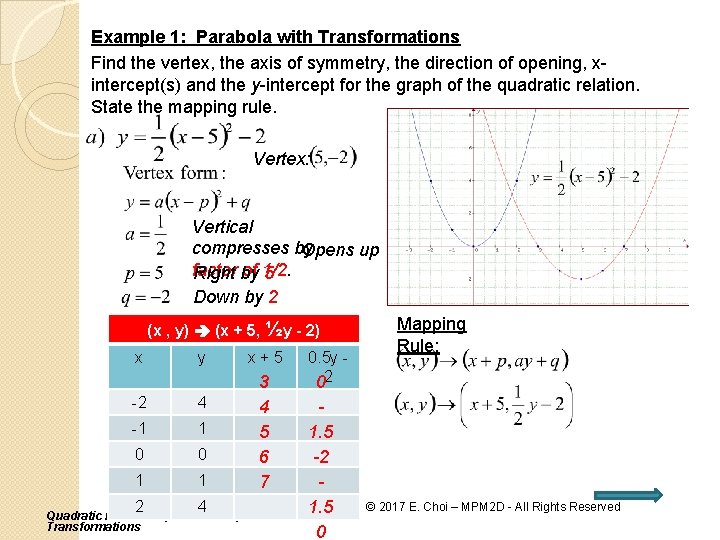
Example 1: Parabola with Transformations Find the vertex, the axis of symmetry, the direction of opening, xintercept(s) and the y-intercept for the graph of the quadratic relation. State the mapping rule. Vertex: Vertical compresses by Opens up factor of 1/2. Right by 5 Down by 2 (x , , y) y) (x + 5, ½y - 2) (x yy xx x+5 0. 5 y -2 4 3 02 -2 -1 -1 0 14 01 01 12 10 41 2 4 Quadratic Relations (Vertex Form): Transformations 4 5 6 7 1. 5 -2 1. 5 0 Mapping Rule: © 2017 E. Choi – MPM 2 D - All Rights Reserved

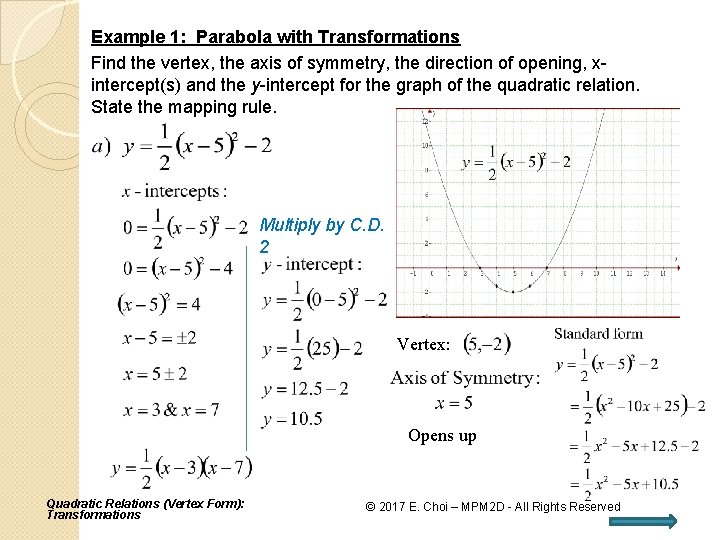
Example 1: Parabola with Transformations Find the vertex, the axis of symmetry, the direction of opening, xintercept(s) and the y-intercept for the graph of the quadratic relation. State the mapping rule. Multiply by C. D. 2 Vertex: Opens up Quadratic Relations (Vertex Form): Transformations © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 1: Parabola with Transformations Find the vertex, the axis of symmetry, the direction of opening, xintercept(s) and the y-intercept for the graph of the quadratic relation. State the mapping rule. Vertex: Vertical expands by factor of 2. Opens down Left by 3 Up by 4 (x (x , , y) y) (x - 3, -2 y + 4) xx yy x-3 -2 -2 44 -1 -1 11 00 00 11 11 22 44 -5 -4 -3 -2 -1 Quadratic Relations (Vertex Form): Transformations -2 y + 4 Mapping Rule: -4 2 -4 © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 1: Parabola with Transformations Find the vertex, the axis of symmetry, the direction of opening, xintercept(s) and the y-intercept for the graph of the quadratic relation. State the mapping rule. Opens down Vertex: Quadratic Relations (Vertex Form): Transformations © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 1: Parabola with Transformations Find the vertex, the axis of symmetry, the direction of opening, xintercept(s) and the y-intercept for the graph of the quadratic relation. State the mapping rule. Vertex: Vertical Opens down compresses by factor Left byof 11/3. Down by 2 (x (x, , y) y) (x - 1, -1/3 y - 2) x yy -2 -2 -1 4 -1 0 0 1 01 10 14 1 2 41 Quadratic Relations 2 (Vertex Form): 4 Transformations x-1 -3 -2 -1 0 1 -1/3 y 2 Mapping Rule: -3 1/3 -2 -2 1/3 -3 1/3 © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 1: Parabola with Transformations Find the vertex, the axis of symmetry, the direction of opening, xintercept(s) and the y-intercept for the graph of the quadratic relation. State the mapping rule. Multiply by C. D. 3 Vertex: Opens down Quadratic Relations (Vertex Form): Transformations © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 2: Parabola with Transformations Determine a quadratic relation in vertex form which contains vertex (-4, -5) and passes through the point (2, -6). Determine the mapping rule for the transformations. Mapping Rule: Parabola compresses vertically by factor of , Quadratic Relations (Vertex Form): Transformations opens (concaves) down (Reflects about x-axis), © 2017 E. Choi – MPM 2 D Rights Reserved translates 4 units left- All and down 5 units.

Homework Work sheet: Day 1: Quadratic Relations in Vertex Form (Transformations) Day 2: Graphing Quadratic Relations in Vertex Form Text: Check the website for updates Quadratic Relations (Vertex Form): Transformations © 2017 E. Choi – MPM 2 D - All Rights Reserved