Grade 10 Academic MPM 2 D Unit 2

Grade 10 Academic (MPM 2 D) Unit 2: Analytic Geometry Properties of Triangles and Quadrilaterals Mr. Choi © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Triangles • Pythagorean Theorem used to find the length of sides of a right triangle Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

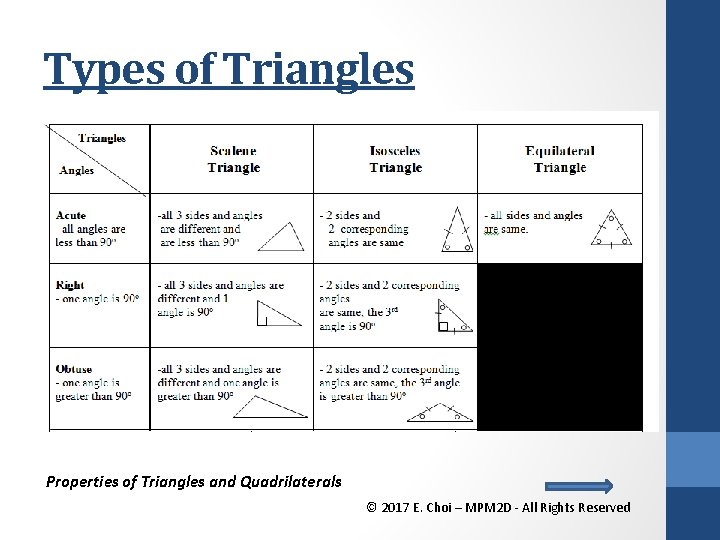
Types of Triangles Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Some Triangles Theorems Sum of Angles in a Triangle Theorem (SATT) (Supplementary angles) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

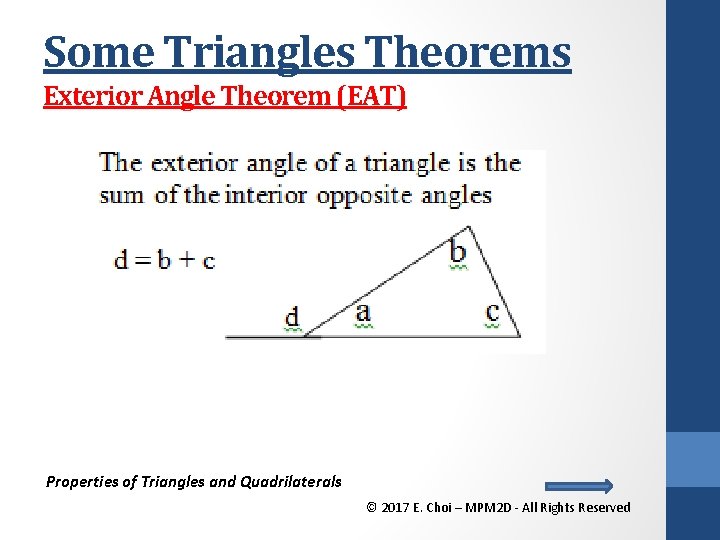
Some Triangles Theorems Exterior Angle Theorem (EAT) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

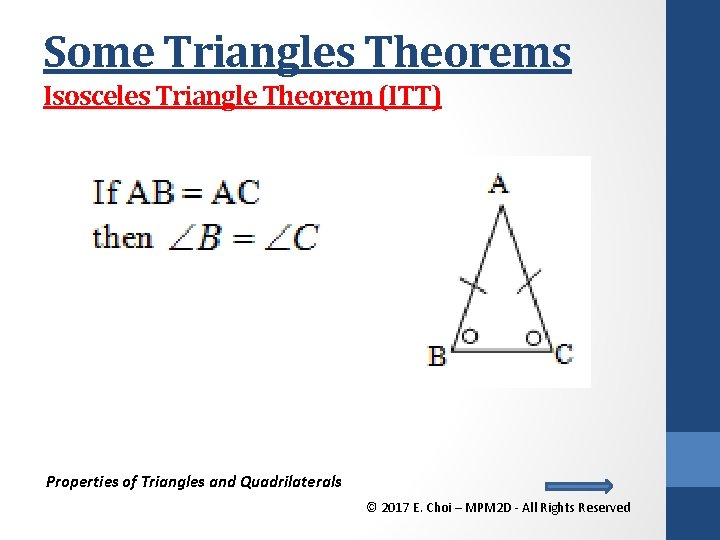
Some Triangles Theorems Isosceles Triangle Theorem (ITT) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Some Angles Theorems Complementary Angles (CA) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Some Angles Theorems Supplementary Angles (SA) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Some Angles Theorems Opposite Angle Theorem(OAT) Angles Sum of a Point Theorem Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Some Angles Theorems Sum of Angles in a Triangle Theorem(SATT) (Supplementary angles) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Parallel Lines Theorems Alternate Angles (PLT-Z) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Parallel Lines Theorems Corresponding Angles (PLT-F) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

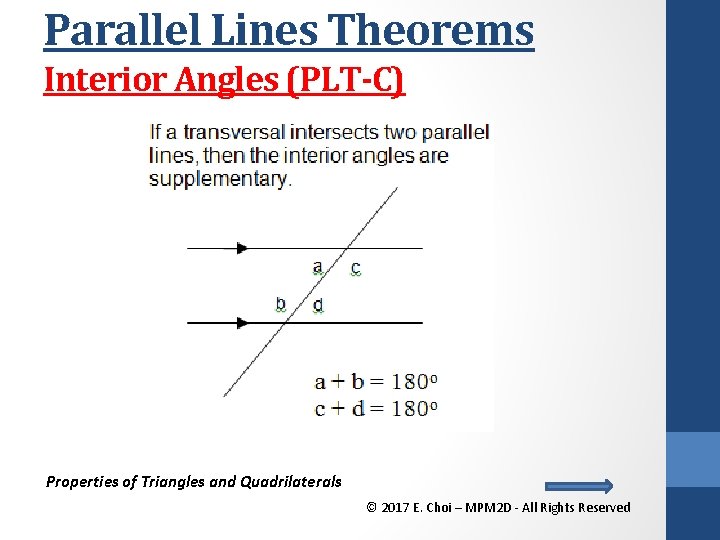
Parallel Lines Theorems Interior Angles (PLT-C) Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Triangles Medians: Midpoint: Altitude: Perpendicular bisectors: Angle bisectors: Centroid: Orthocentre: Circumcentre: Incentre: line from vertex to the midpoint of the opposite side point on a line that divides it into 2 equal parts to draw a median find mid point of opposite side and connect to vertex shows the height of a polygon to draw an altitude line from vertex to opposite side so that it meets at 90° perpendicular to a line segment and meets at its midpoint. to draw a perpendicular bisector find midpoint, then measure a right angle, draw line. The (interior) bisector of an angle, also called the internal angle bisector is the line or line segment that divides the angle into two equal parts where all 3 medians meet divides each median in the ratio 1: 2 it is the centre of mass where all 3 altitudes meet where all 3 perpendicular bisectors meet centre of the circle that passes through the vertices of the triangle the circle is called circumcircle or circumscribed circle where all 3 angle bisectors meet centre of the circle that meets each side once the circle is called incircle or inscribed circle Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

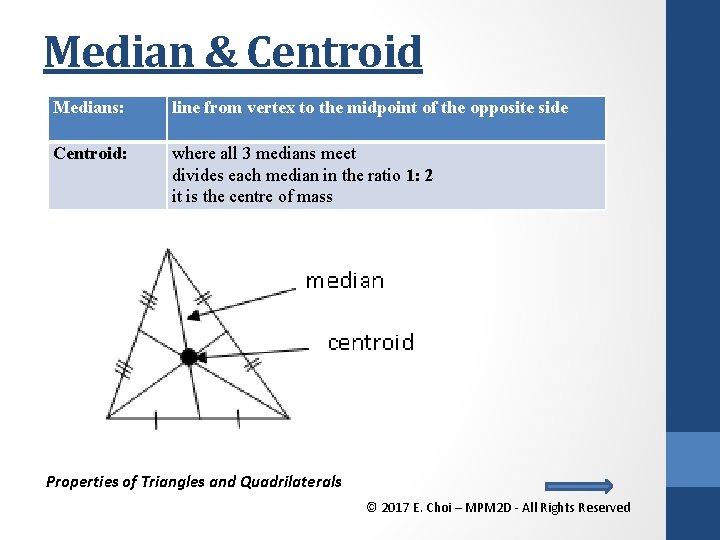
Median & Centroid Medians: line from vertex to the midpoint of the opposite side Centroid: where all 3 medians meet divides each median in the ratio 1: 2 it is the centre of mass Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

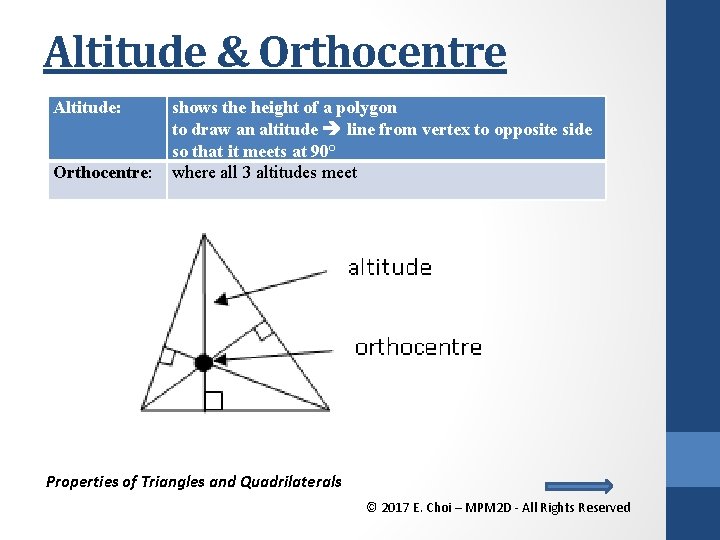
Altitude & Orthocentre Altitude: Orthocentre: shows the height of a polygon to draw an altitude line from vertex to opposite side so that it meets at 90° where all 3 altitudes meet Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

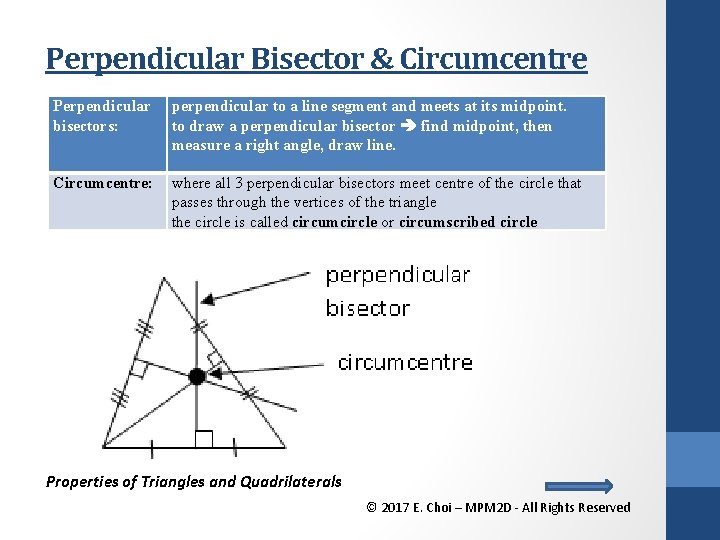
Perpendicular Bisector & Circumcentre Perpendicular bisectors: perpendicular to a line segment and meets at its midpoint. to draw a perpendicular bisector find midpoint, then measure a right angle, draw line. Circumcentre: where all 3 perpendicular bisectors meet centre of the circle that passes through the vertices of the triangle the circle is called circumcircle or circumscribed circle Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

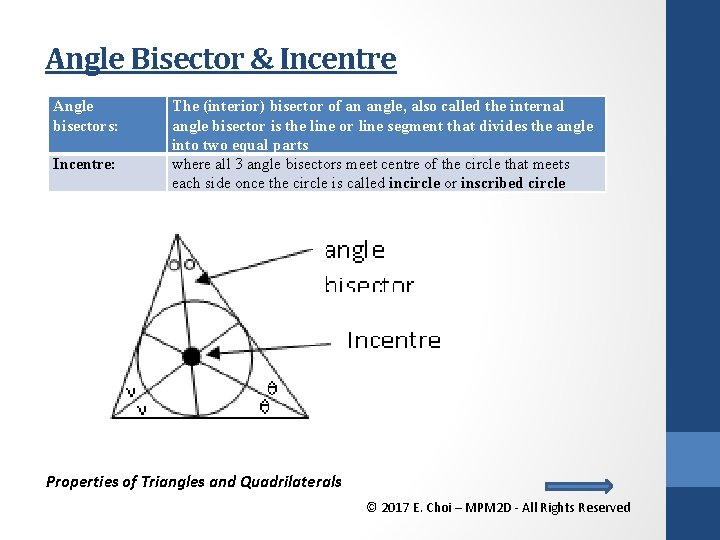
Angle Bisector & Incentre Angle bisectors: Incentre: The (interior) bisector of an angle, also called the internal angle bisector is the line or line segment that divides the angle into two equal parts where all 3 angle bisectors meet centre of the circle that meets each side once the circle is called incircle or inscribed circle Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Quadrilaterals What is a quadrilateral? Polygon with 4 sides and sum of the angles is 360 o Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Quadrilaterals Quadrilateral Square Rectangle Picture Description & Properties Quadrilateral with 4 sides are equal All angles are 90 o Diagonals are perpendicular to each other Quadrilateral with 2 pairs of equal opposite sides All angles are 90 o Diagonals are not perpendicular to each other Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Quadrilaterals Quadrilateral Rhombus Parallelogram Picture Description & Properties Quadrilateral with 4 sides are equal None of angles is 90 o A pair of acute angles and a pair of obtuse angles Diagonals are perpendicular to each other Quadrilateral with 2 pairs of equal opposite sides None of angles is 90 o A pair of acute angles and a pair of obtuse angles Diagonals are not perpendicular to each other Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Quadrilaterals Quadrilateral Picture Description & Properties Quadrilateral with 2 pairs of equal adjacent sides Diagonals are perpendicular to each other Quadrilateral with 1 pair of unequal but parallel opposite sides Kite Trapezoid Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

Homework Work sheet: Cartesian Triangles - A Summary Text: • Read P. 33 & 38. Make Summary notes • P. 34 #1 - 4 • P. 39 #1, 2, 4, 5, 6 • Read P. 36. Make Summary notes • P. 37 #1, 2, 3, 4, 6, 7 Check the website for updates Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved

End of lesson Properties of Triangles and Quadrilaterals © 2017 E. Choi – MPM 2 D - All Rights Reserved