Grade 10 Academic MPM 2 D Unit 2








- Slides: 14

Grade 10 Academic (MPM 2 D) Unit 2: Analytic Geometry Perpendicular Bisector & Circumcentre Mr. Choi © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Triangles Medians: Midpoint: Altitude: Perpendicular bisectors: Angle bisectors: Centroid: Orthocentre: Circumcentre: Incentre: line from vertex to the midpoint of the opposite side point on a line that divides it into 2 equal parts to draw a median find mid point of opposite side and connect to vertex shows the height of a polygon to draw an altitude line from vertex to opposite side so that it meets at 90° perpendicular to a line segment and meets at its midpoint. to draw a perpendicular bisector find midpoint, then measure a right angle, draw line. The (interior) bisector of an angle, also called the internal angle bisector is the line or line segment that divides the angle into two equal parts where all 3 medians meet divides each median in the ratio 1: 2 it is the centre of mass where all 3 altitudes meet where all 3 perpendicular bisectors meet centre of the circle that passes through the vertices of the triangle the circle is called circumcircle or circumscribed circle where all 3 angle bisectors meet centre of the circle that meets each side once the circle is called incircle or inscribed circle Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

Perpendicular Bisector & Circumcentre Perpendicular bisectors: Circumcentre: perpendicular to a line segment and meets at its midpoint. to draw a perpendicular bisector find midpoint, then measure a right angle, draw line. where all 3 perpendicular bisectors meet centre of the circle that passes through the vertices of the triangle the circle is called circumcircle or circumscribed circle perpendicular bisector circumcentre circumcircle Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

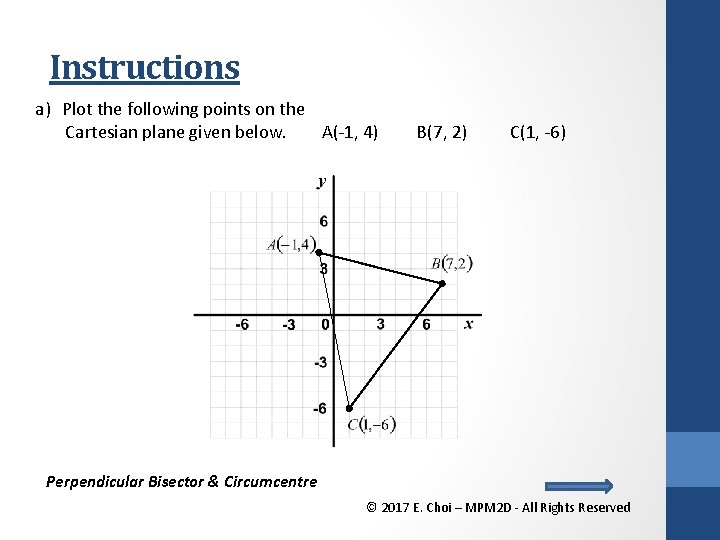
Instructions a) Plot the following points on the Cartesian plane given below. A(-1, 4) B(7, 2) C(1, -6) b) Draw a line perpendicular to BC from D. c) Determine the slope and equation of this line. d) What is this line called? e) Repeat steps (b) to (e) for the other two sides. f) Prove that the Perpendicular bisectors of a triangle pass through the same point. g) What is that point called? Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

Instructions a) Plot the following points on the Cartesian plane given below. A(-1, 4) B(7, 2) C(1, -6) Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

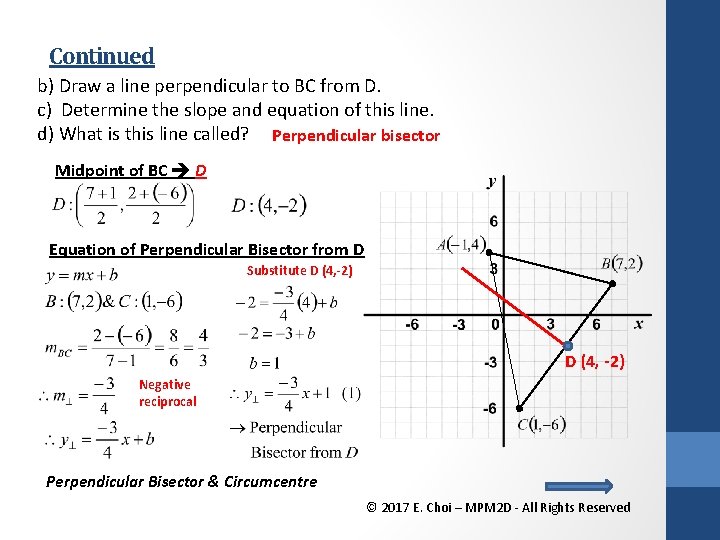
Continued b) Draw a line perpendicular to BC from D. c) Determine the slope and equation of this line. d) What is this line called? Perpendicular bisector Midpoint of BC D Equation of Perpendicular Bisector from D Substitute D (4, -2) Negative reciprocal Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

Or using the slope from midpoint up 1, right 5 Continued f) Repeat steps b to e for the other 2 perpendicular bisectors from E and F. Midpoint of AC E Equation of Perpendicular Bisector from E Substitute E (0, -1) Negative reciprocal D (4, -2) Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

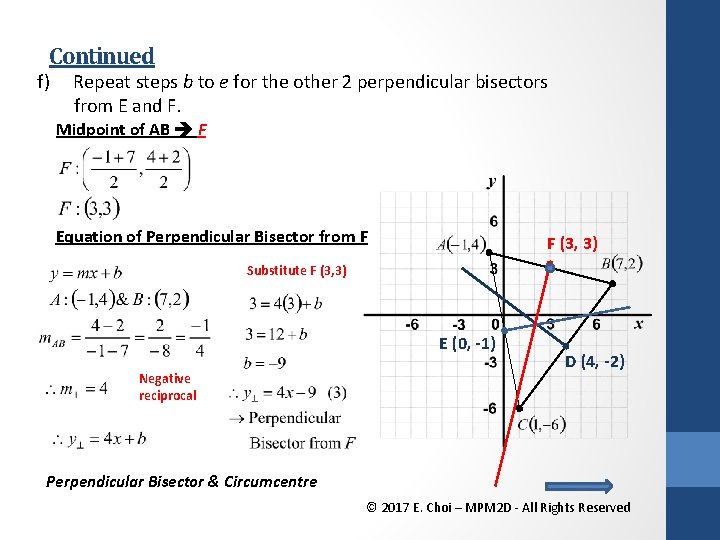
Continued f) Repeat steps b to e for the other 2 perpendicular bisectors from E and F. Midpoint of AB F Equation of Perpendicular Bisector from F F (3, 3) Substitute F (3, 3) E (0, -1) Negative reciprocal D (4, -2) Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

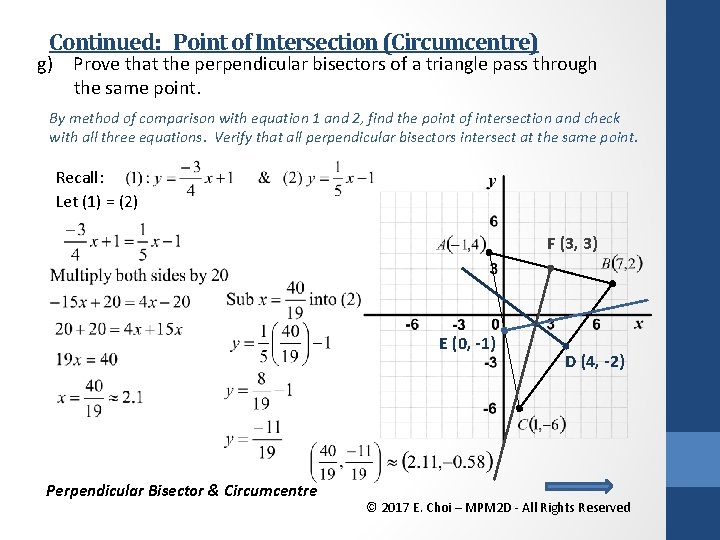
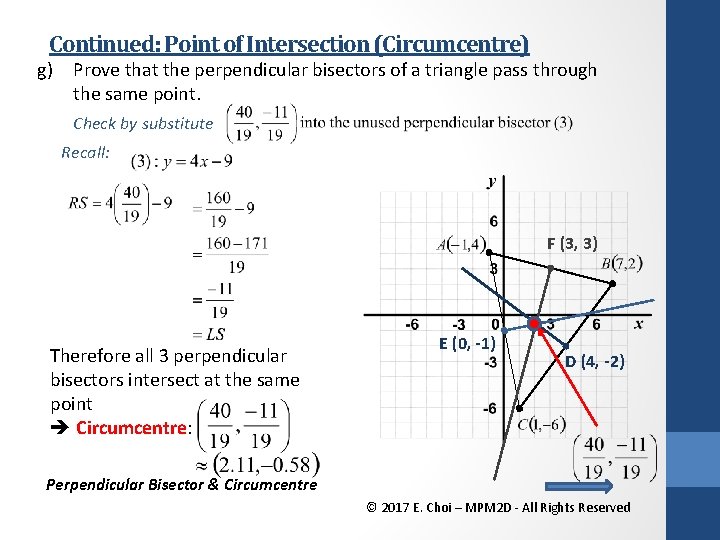
Continued: Point of Intersection (Circumcentre) g) Prove that the perpendicular bisectors of a triangle pass through the same point. By method of comparison with equation 1 and 2, find the point of intersection and check with all three equations. Verify that all perpendicular bisectors intersect at the same point. Recall: Let (1) = (2) F (3, 3) E (0, -1) Perpendicular Bisector & Circumcentre D (4, -2) © 2017 E. Choi – MPM 2 D - All Rights Reserved

Continued: Point of Intersection (Circumcentre) g) Prove that the perpendicular bisectors of a triangle pass through the same point. Check by substitute Recall: F (3, 3) Therefore all 3 perpendicular bisectors intersect at the same point Circumcentre: E (0, -1) D (4, -2) Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

Perpendicular Bisector & Circumcentre Perpendicular bisectors: Circumcentre: perpendicular to a line segment and meets at its midpoint. to draw a perpendicular bisector find midpoint, then measure a right angle, draw line. where all 3 perpendicular bisectors meet centre of the circle that passes through the vertices of the triangle the circle is called circumcircle or circumscribed circle perpendicular bisector circumcentre circumcircle Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

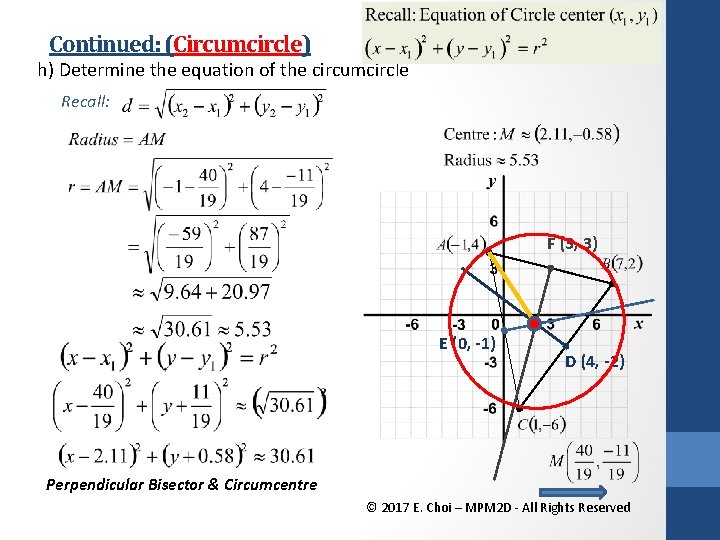
Continued: (Circumcircle) h) Determine the equation of the circumcircle Recall: F (3, 3) E (0, -1) D (4, -2) Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

Homework Work sheet: Extra practice #1 a-d Text: • P. 173 # 4, 5, 12, 15, 18 • P. 194 #3, 10, 14, 16 • Check the website for updates Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved

End of lesson Perpendicular Bisector & Circumcentre © 2017 E. Choi – MPM 2 D - All Rights Reserved