GPU Implementations for Finite Element Methods Brian S

GPU Implementations for Finite Element Methods Brian S. Cohen 12 December 2016

Last Time… CPU Time [s] Stiffness Matrix Assembly 10 2 10 1 10 0 10 -1 10 -2 10 -3 10 -4 10 Julia v 0. 47 MATLAB v 2016 b 2 10 3 10 4 10 5 10 6 10 7 Number of DOFs B. Cohen – 02 December 2020 Slide 2

Goals 1. Implement an efficient GPU-based assembly routine to interface with the Elliptic. FEM. jl package – Speed test all implementations and compare against CPU algorithm using varied mesh densities – Investigate where GPU implementation choke points are and how these can be improved in the future 2. Implement a GPU-based linear solver routine – Speed test solver and compare against CPU algorithm B. Cohen – 02 December 2020 Slide 3

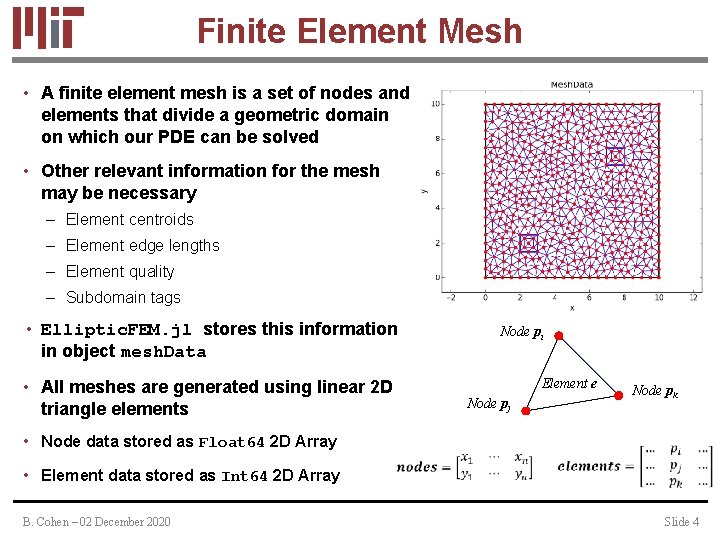
Finite Element Mesh • A finite element mesh is a set of nodes and elements that divide a geometric domain on which our PDE can be solved • Other relevant information for the mesh may be necessary – Element centroids – Element edge lengths – Element quality – Subdomain tags • Elliptic. FEM. jl stores this information in object mesh. Data Element e • All meshes are generated using linear 2 D triangle elements Node pj • Node data stored as Float 64 2 D Array • Element data stored as Int 64 2 D Array B. Cohen – 02 December 2020 Node pi Node pk Slide 4

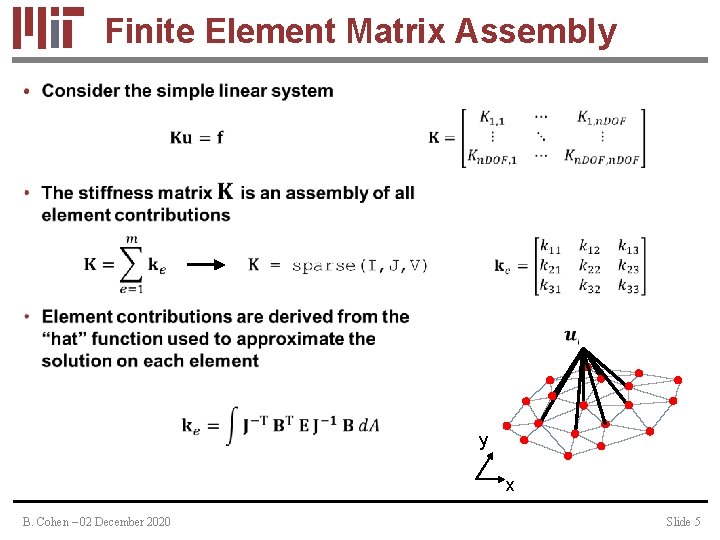
Finite Element Matrix Assembly • y x B. Cohen – 02 December 2020 Slide 5

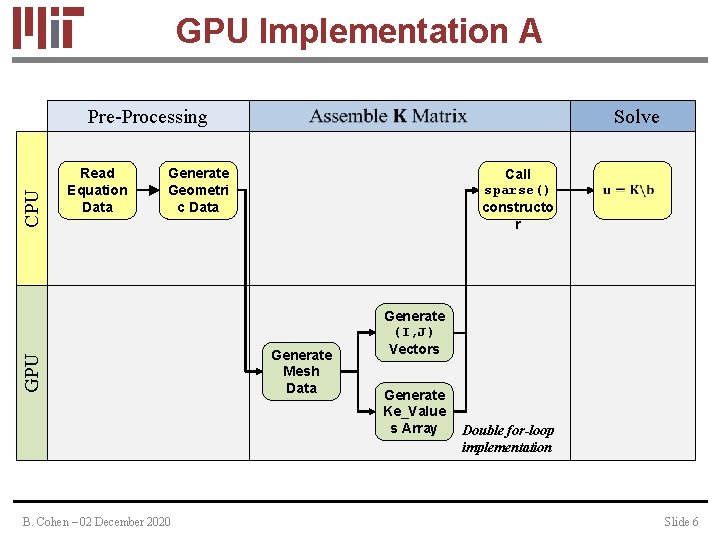
GPU Implementation A Read Equation Data Solve Generate Geometri c Data GPU CPU Pre-Processing B. Cohen – 02 December 2020 Call sparse() constructo r Generate Mesh Data Generate (I, J) Vectors Generate Ke_Value s Array Double for-loop implementation Slide 6

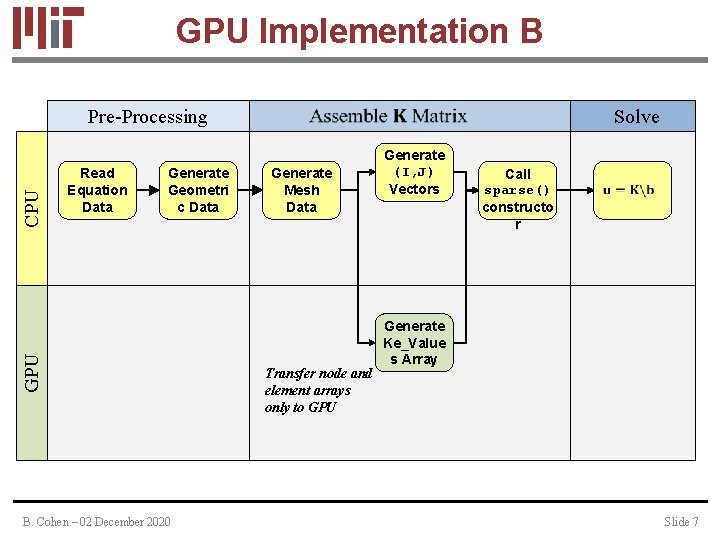
GPU Implementation B Read Equation Data Generate Geometri c Data GPU CPU Pre-Processing B. Cohen – 02 December 2020 Solve Generate Mesh Data Transfer node and element arrays only to GPU Generate (I, J) Vectors Call sparse() constructo r Generate Ke_Value s Array Slide 7

CPU Time for I, J, V Assembly [s] CPU vs. GPU Implementations 10 2 10 1 10 CPU Implementation GPU Implementation A GPU Implementation B 0 10 -1 10 -2 10 -3 10 -4 10 2 10 3 10 4 10 5 10 6 10 7 Number of DOFs • Ge. Force GTX 765 M, 2048 MB B. Cohen – 02 December 2020 Slide 8

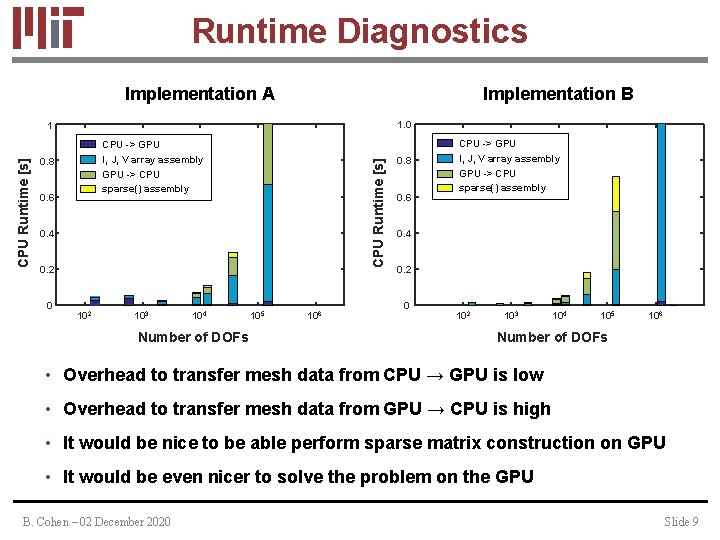
Runtime Diagnostics Implementation A Implementation B 1. 0 CPU -> GPU I, J, V array assembly GPU -> CPU sparse() assembly 0. 8 0. 6 CPU Runtime [s] 1 0. 4 0. 2 0 102 103 104 Number of DOFs 105 106 0. 8 0. 6 CPU -> GPU I, J, V array assembly GPU -> CPU sparse() assembly 0. 4 0. 2 0 102 103 104 105 106 Number of DOFs • Overhead to transfer mesh data from CPU → GPU is low • Overhead to transfer mesh data from GPU → CPU is high • It would be nice to be able perform sparse matrix construction on GPU • It would be even nicer to solve the problem on the GPU B. Cohen – 02 December 2020 Slide 9

Solving the Model • Now we want to solve the linear model: • Array. Fire. jl does not currently support sparse matrices – Dense matrix operations seem to be comparable in speed or slower on GPU’s than CPU’s • CUSPARSE. jl wraps NVIDIA CUSPARSE library functions – High performance sparse linear algebra library – Does not wrap any solver routines • Built on CUDArt. jl package – Wraps the CUDA runtime API • Both packages required CUDA Toolkit (v 8. 0) B. Cohen – 02 December 2020 Slide 10

GPU Solver Implementation • B. Cohen – 02 December 2020 Slide 11

CPU Time to Solve Ku=f [s] Solver Results 10 2 10 1 10 0 CPU Implementation GPU Implementation 10 -1 10 -2 10 -3 10 -4 10 2 10 3 10 4 10 5 10 6 10 7 Number of DOFs B. Cohen – 02 December 2020 Slide 12

Conclusion • GPU computing in Julia shows promise of speeding up FEM matrix assembly and solve routines – Potentially greater gains to be made with higher order 2 D/3 D elements – Minimize data transfer to the GPU needed to assemble FEM matrices – Keeping code vectorized helps – Removing any temporary data copies on GPU • Array. Fire. jl should (and hopefully soon will) support sparse matrix assembly and arithmetic – Open issue on Git. Hub since late September, 2016 • CUSPARSE. jl should (and hopefully soon will) wrap additional functions – COO matrix constructor and iterative solvers would be especially useful • Large impact on optimization problems where matrix assembly routines and solvers are called many times B. Cohen – 02 December 2020 Slide 13