Good Afternoon Please have a blank sheet of

Good Afternoon! �Please have a blank sheet of paper, writing utensil and graphing calculator on your desk BEFORE the bell rings!!

Using the QUADRATIC FORMULA, complete the following… 1. f(x) = x 2 + 4 x + 10 2. x 2 + x + 1 = 0 3. 2 x 2 + 7 x – 13 = 0 4. x 2 – 2 x + 4 = 0

Complex Numbers and Roots Sections 5. 5 and 5. 9

PURE IMAGINARY NUMBERS � Pure Imaginary Numbers – Square Roots of negative numbers. � Imaginary numbers can be written in the form bi, where b is a real number and i is the imaginary unit. �i = _____ i 2 = _____ i 3 = _____ � Examples: 1. Simplify i 14 = ____ 3. Simplify i 40 = ____ 2. Simplify i 21= ____ 4. Simplify i 53 =_____ i 4 = _____

In your calculator, compute the following: �i 51 �i 52 �i 53 �i 54

Multiplying Imaginary Numbers �

Simplify in terms of i �

Solving a Quadratic with Imaginary Solutions 5. 6. 7.

�Complex Number – a number that can be written in the form a+bi , where a and b are real numbers and. �Every complex number has a real part a and an imaginary part b. �Two complex numbers are equal if and only if their real parts and their imaginary parts are equal.

Equating Two Complex Numbers �

Complex Conjugates � Complex Conjugates – real parts are equal and imaginary parts are opposites �The complex conjugate of any complex number a + bi is the complex number a - bi �If a quadratic equation with real coefficients has nonreal roots, those roots are complex conjugates. Find each complex conjugate. 1. Write as a + bi 2. Find a – bi 3. Simplify

Examples: Complex Conjugate �

Graphing Complex Numbers �Graphing complex numbers is like graphing real numbers. �Complex Plane: The real axis corresponds to the x-axis and the imaginary axis corresponds to the y-axis. Complex plane: The coordinate plane for imaginary numbers
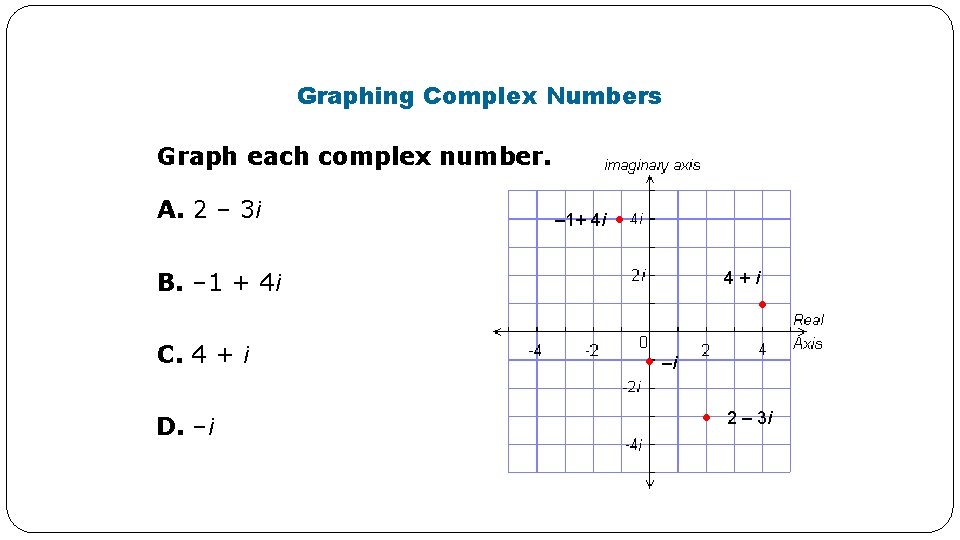
Graphing Complex Numbers Graph each complex number. A. 2 – 3 i – 1+ 4 i • B. – 1 + 4 i C. 4 + i D. –i 4+i • • –i • 2 – 3 i

Recall that absolute value of a real number is its distance from 0 on the real axis, which is also a number line. Similarly, the absolute value of an imaginary number is its distance from 0 along the imaginary axis.

Determining the Absolute Value of Complex Numbers Find each absolute value. A. |3 + 5 i| B. |1 – 2 i| C. |– 7 i| |0 +(– 7)i| 7

Adding Subtracting Multiplying USE THE CALCULATOR!!!!

Adding and Subtracting Complex Numbers �Examples: � 12. Simplify (6 – 4 i) + (1 + 3 i) = � 13. Simplify (3 – 2 i) – (5 – 4 i) = � 14. Simplify ( 3 – 4 i) – (1 – 4 i) =
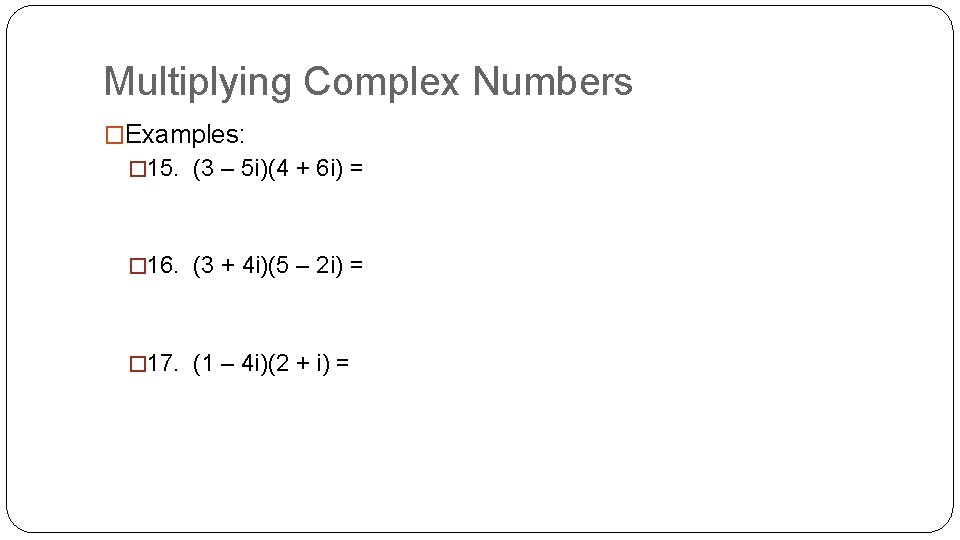
Multiplying Complex Numbers �Examples: � 15. (3 – 5 i)(4 + 6 i) = � 16. (3 + 4 i)(5 – 2 i) = � 17. (1 – 4 i)(2 + i) =

Dividing Complex Numbers - Dividing complex numbers can be done in the graphing calculator. - Simply add ( ) around the top and bottom and use the / key. You may have to hit “math, enter” to change some answers back to correct simplified form. �Examples: 22. Simplify 24. Simplify 23. Simplify 25. Simplify

Finding Complex Zeros of Quadratic Functions Find the zeros of the function. f(x) = x 2 + 10 x + 26 = 0 Set equal to 0. x 2 + 10 x + Rewrite. = – 26 + x 2 + 10 x + 25 = – 26 + 25 (x + 5)2 = – 1 Add to both sides. Factor. Take square roots. Simplify.

Finding Complex Zeros of Quadratic Functions Find the zeros of the function. g(x) = x 2 + 4 x + 12 = 0 Set equal to 0. x 2 + 4 x + Rewrite. = – 12 + x 2 + 4 x + 4 = – 12 + 4 (x + 2)2 = – 8 Add to both sides. Factor. Take square roots. Simplify.

Finding Complex Zeros of Quadratic Functions Find the zeros of the function. f(x) = x 2 + 4 x + 13 = 0 Set equal to 0. x 2 + 4 x + Rewrite. = – 13 + x 2 + 4 x + 4 = – 13 + 4 (x + 2)2 = – 9 Add to both sides. Factor. Take square roots. x = – 2 ± 3 i Simplify.

Finding Complex Zeros of Quadratic Functions Find the zeros of the function. g(x) = x 2 – 8 x + 18 = 0 Set equal to 0. x 2 – 8 x + Rewrite. = – 18 + x 2 – 8 x + 16 = – 18 + 16 Add to both sides. Factor. Take square roots. Simplify.
- Slides: 24