Goniometrick funkce Tangens Dostupn z Metodickho portlu www

Goniometrické funkce Tangens Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

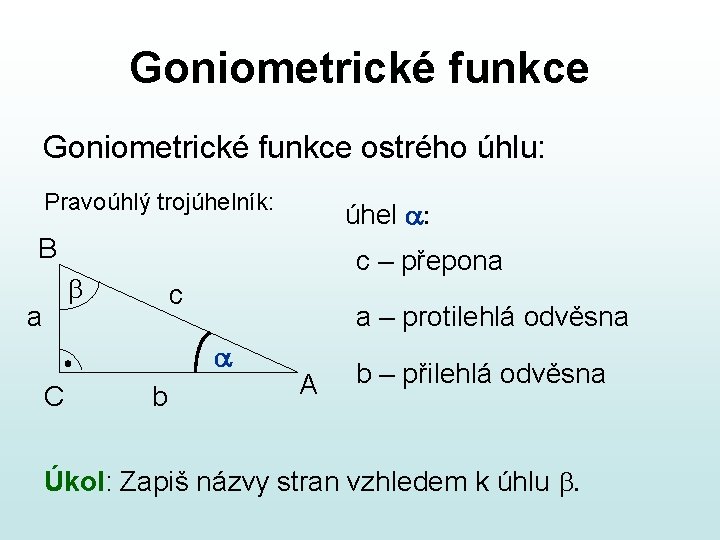
Goniometrické funkce ostrého úhlu: Pravoúhlý trojúhelník: úhel a: B c – přepona b a c a – protilehlá odvěsna a C b A b – přilehlá odvěsna Úkol: Zapiš názvy stran vzhledem k úhlu b.

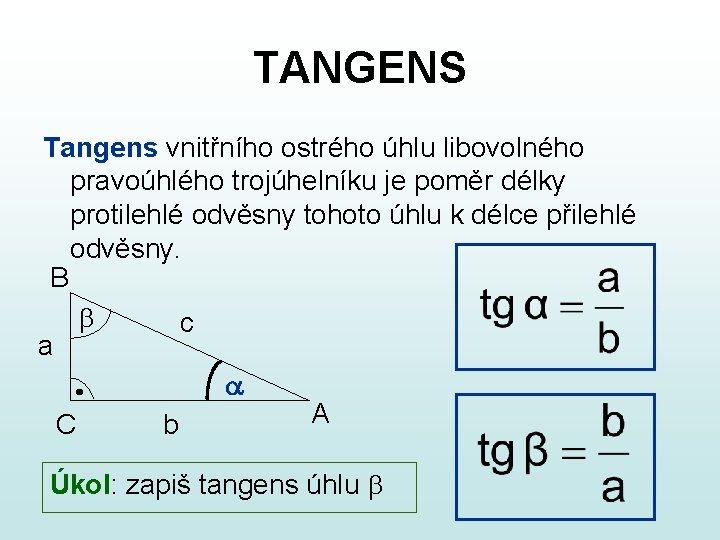
TANGENS Tangens vnitřního ostrého úhlu libovolného pravoúhlého trojúhelníku je poměr délky protilehlé odvěsny tohoto úhlu k délce přilehlé odvěsny. B b c a a A C b Úkol: zapiš tangens úhlu b

TANGENS Každému ostrému úhlu přísluší právě jedna hodnota funkce tangens. Poznámka: tangens ostrého úhlu může být i větší než jedna. Zdůvodni proč? Protože délka jedné odvěsny není vždy menší než délka druhé odvěsny. Úkol: Sestrojte graf funkce tangens. (použij tabulky, kalkulačku, milimetrový papír)

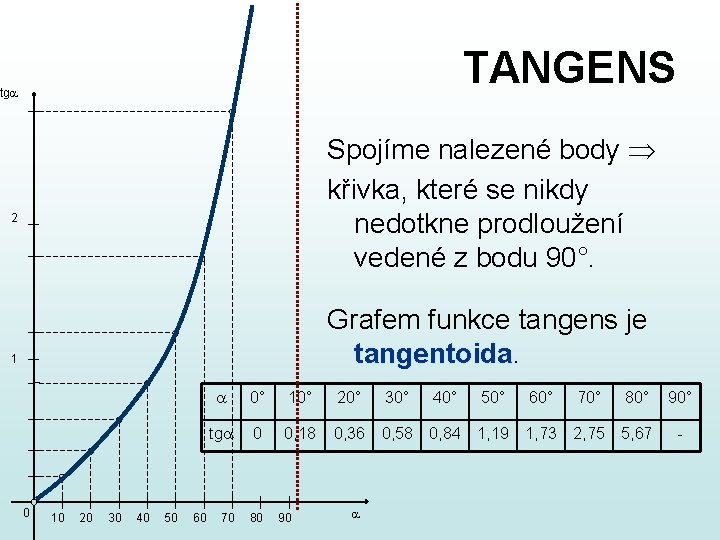
TANGENS tga Spojíme nalezené body křivka, které se nikdy nedotkne prodloužení vedené z bodu 90°. 2 Grafem funkce tangens je tangentoida. 1 0 10 20 30 40 50 60 a 0° 10° 20° 30° 40° 50° 60° 70° 80° 90° tga 0 0, 18 0, 36 0, 58 0, 84 1, 19 1, 73 2, 75 5, 67 - 70 80 90 a

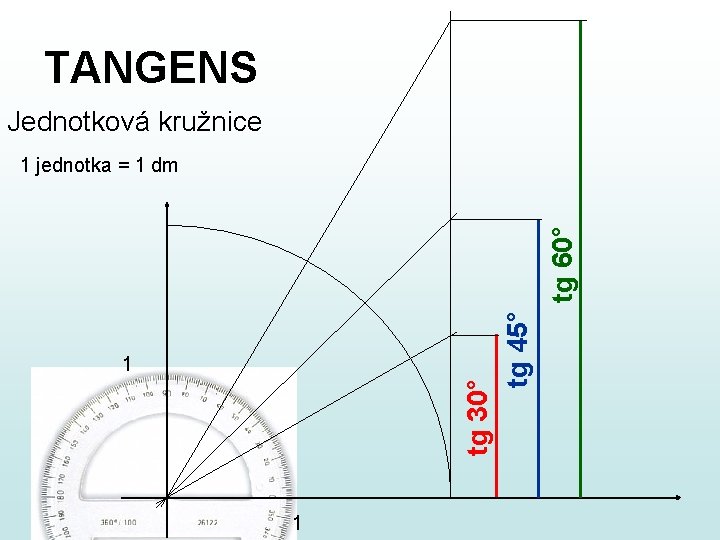
TANGENS Jednotková kružnice tg 30° tg 45° tg 60° 1 jednotka = 1 dm 1 1

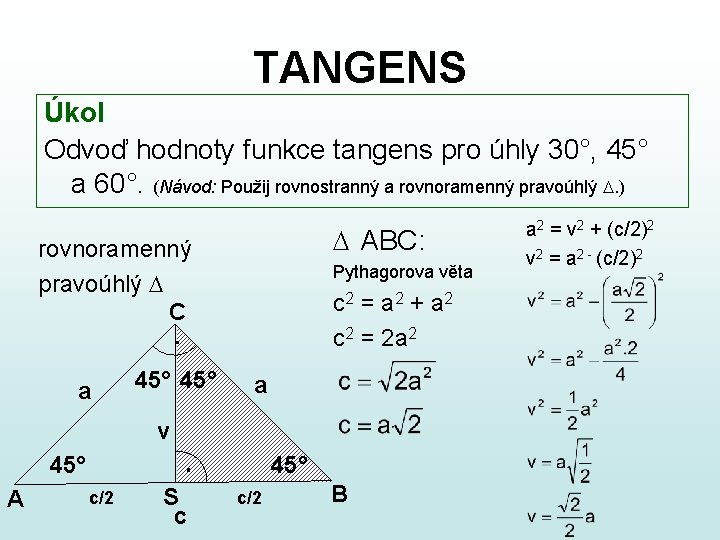
TANGENS Úkol Odvoď hodnoty funkce tangens pro úhly 30°, 45° a 60°. (Návod: Použij rovnostranný a rovnoramenný pravoúhlý . ) ABC: rovnoramenný pravoúhlý C a 45° Pythagorova věta c 2 = a 2 + a 2 c 2 = 2 a 2 a v 45° A 45° c/2 S c c/2 B a 2 = v 2 + (c/2)2 v 2 = a 2 - (c/2)2

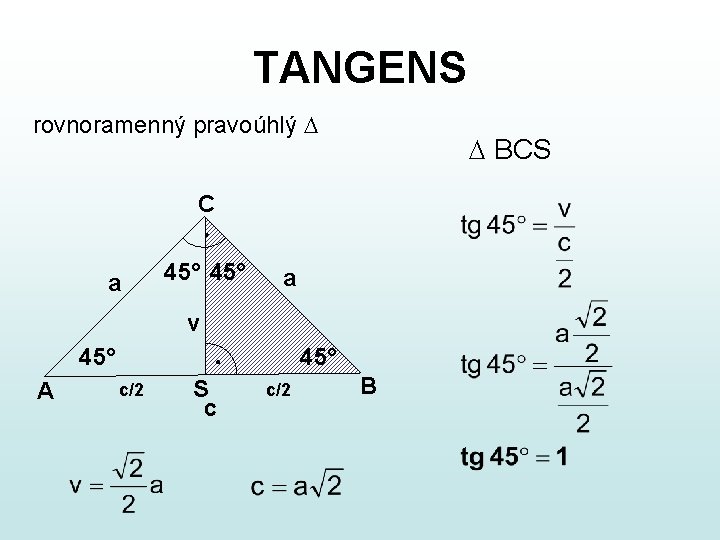
TANGENS rovnoramenný pravoúhlý BCS C a 45° a v 45° A 45° c/2 S c c/2 B

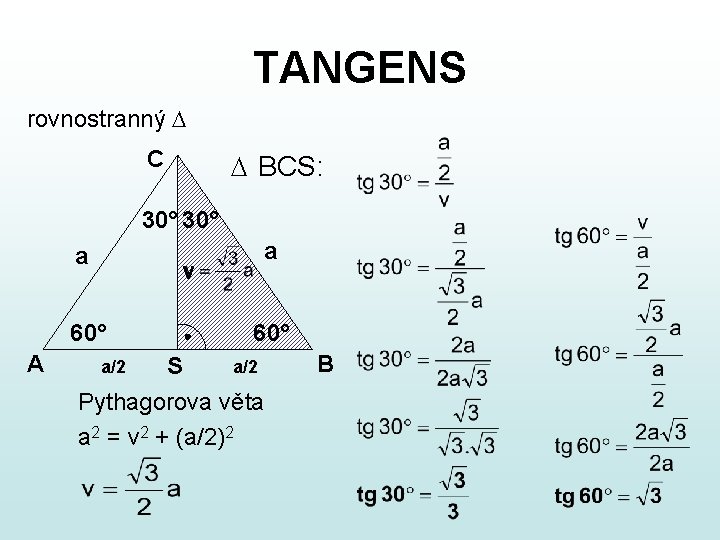
TANGENS rovnostranný C BCS: 30° a v 60° A a 60° a/2 S Pythagorova věta a 2 = v 2 + (a/2)2 a/2 B

TANGENS Tabulka důležitých hodnot funkce tangens a tga 0° 0 30° 45° 1 60° 90° nedefinován

PŘÍKLADY 1. Určete hodnotu tg a, jestliže a) sin a = b) cos a = 2. Vypočítejte obvod pravidelného šestiúhelníku opsaného kružnici s poloměrem r = 4 cm.

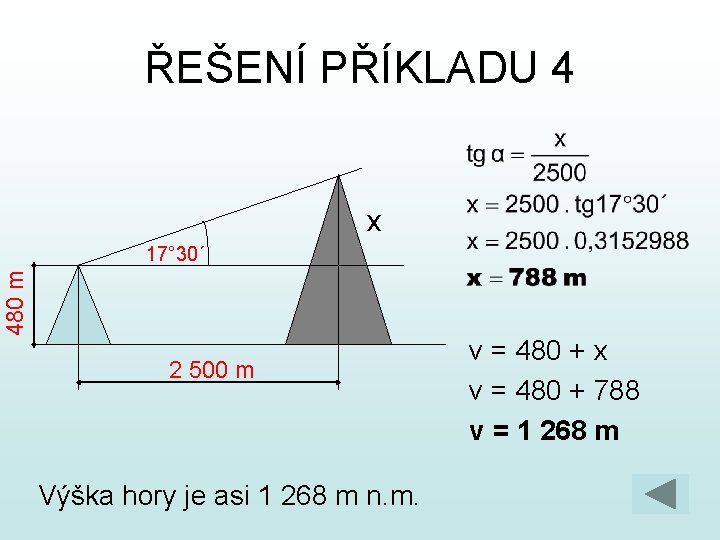
PŘÍKLADY 3. Pod jakým úhlem stoupá schodiště, jestliže každý schod je 30 cm široký a 12 cm vysoký? 4. Vrchol hory, která je od nás vzdálena 2 500 m, vidíme ve výškovém úhlu 17° 30´. Výška pozorovacího místa nad mořem je 480 m. Vypočítejte výšku vrcholu hory nad terénem.

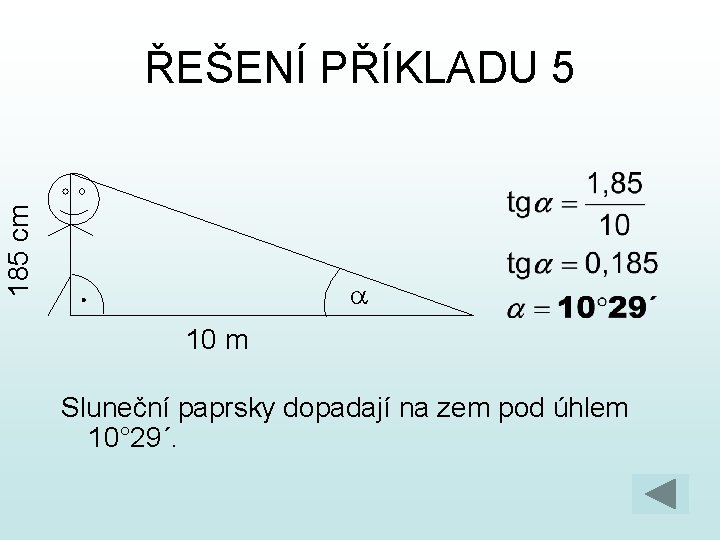
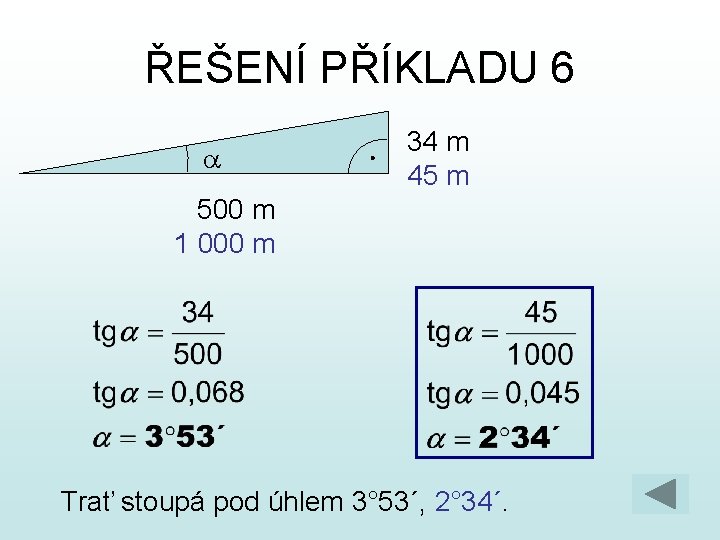
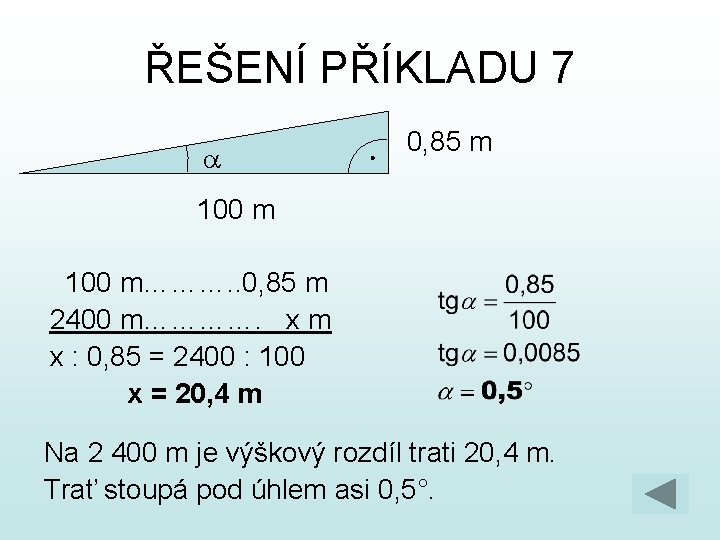
PŘÍKLADY 5. Pod jakým úhlem dopadají sluneční paprsky na povrch země, jestliže člověk (vysoký 185 cm), který stojí vzpřímeně, má stín dlouhý 10 m? 6. Co znamenají vedle železniční trati značky s údajem nebo . Pod jakým úhlem trať stoupá? 7. Železnice má stoupání 8, 5 %. Jaký je výškový rozdíl míst na trati vzdálených od sebe 2 400 m? Pod jakým úhlem trať stoupá?

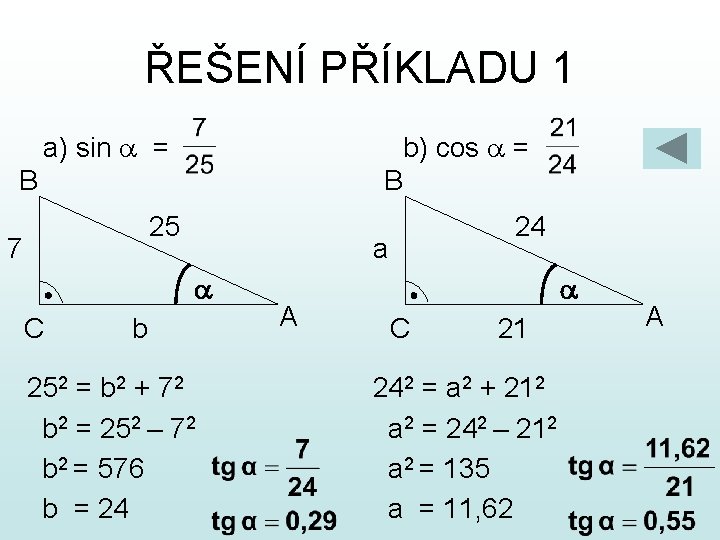
ŘEŠENÍ PŘÍKLADU 1 a) sin a = b) cos a = B B 25 7 a a C 24 b 252 = b 2 + 72 b 2 = 252 – 72 b 2 = 576 b = 24 A a C 21 242 = a 2 + 212 a 2 = 242 – 212 a 2 = 135 a = 11, 62 A

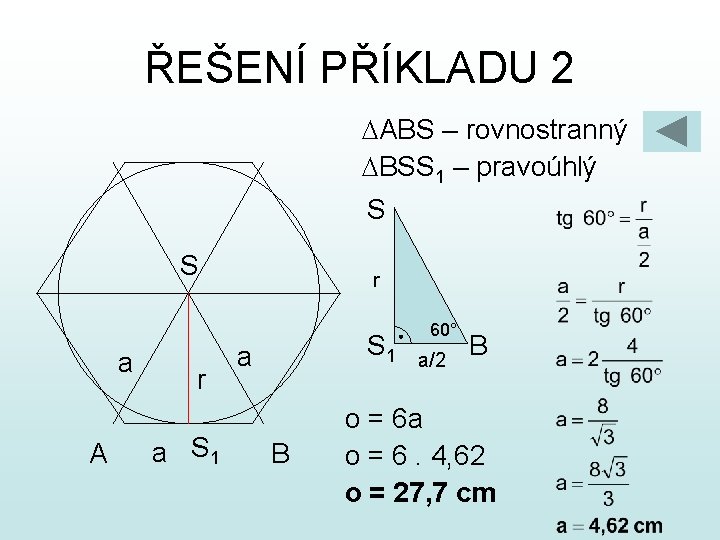
ŘEŠENÍ PŘÍKLADU 2 ABS – rovnostranný BSS 1 – pravoúhlý S S a A r a S 1 r S 1 a B 60° a/2 B o = 6 a o = 6. 4, 62 o = 27, 7 cm

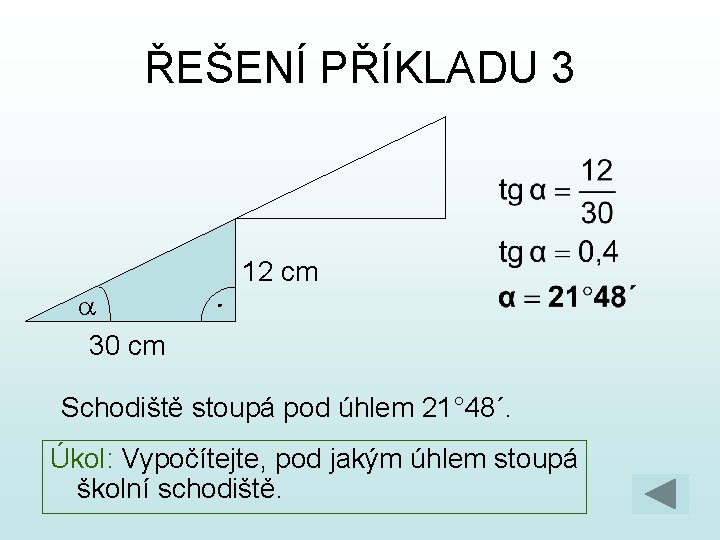
ŘEŠENÍ PŘÍKLADU 3 12 cm a 30 cm Schodiště stoupá pod úhlem 21° 48´. Úkol: Vypočítejte, pod jakým úhlem stoupá školní schodiště.

ŘEŠENÍ PŘÍKLADU 4 480 m x 17° 30´ 2 500 m Výška hory je asi 1 268 m n. m. v = 480 + x v = 480 + 788 v = 1 268 m

185 cm ŘEŠENÍ PŘÍKLADU 5 a 10 m Sluneční paprsky dopadají na zem pod úhlem 10° 29´.

ŘEŠENÍ PŘÍKLADU 6 a 34 m 45 m 500 m 1 000 m Trať stoupá pod úhlem 3° 53´, 2° 34´.

ŘEŠENÍ PŘÍKLADU 7 a 0, 85 m 100 m………. . 0, 85 m 2400 m…………. x m x : 0, 85 = 2400 : 100 x = 20, 4 m Na 2 400 m je výškový rozdíl trati 20, 4 m. Trať stoupá pod úhlem asi 0, 5°.