Going to the World Cup and what it







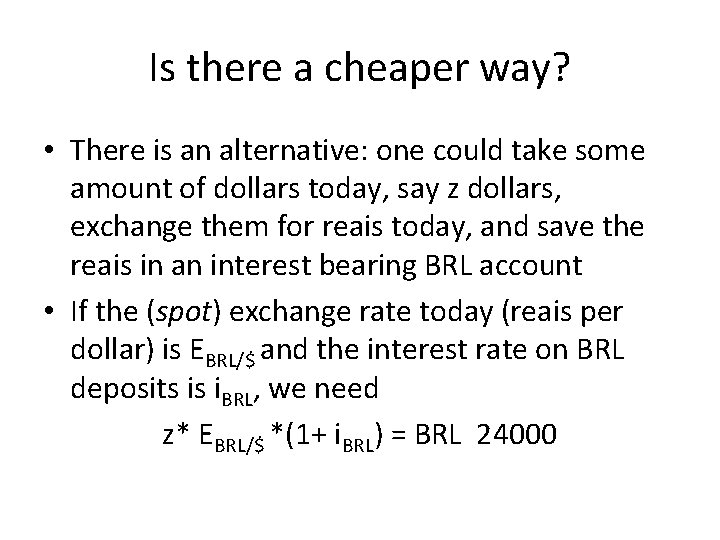





- Slides: 13

Going to the World Cup (and what it says about arbitrage) Roberto Chang January 2014 Econ 336

The “problem” • A number of people I know are thinking about going to Brazil for the World Cup • It is very expensive, so we need to make efficient financing decisions


The exchange rate question • They say they will need, say, about 24000 Brazilian reais (BRL) each, by July (six months from now). • Friday’s spot exchange rate: 2. 40 BRL per US$ • So, at current rates, the amount involved is about US $ 10, 000 • But the BRL/US$ exchange rate can move a lot, we are wondering what is the best way to plan to have that amount for the July trip.

• http: //www. xe. com/currencycharts/? from=USD&to=BRL&view=5 Y

Covering with a forward contract • A forward contract is an agreement to exchange currencies at a given date in the future, at a given price (the forward rate) • So, one way to have 24000 BRL in six months is to set aside today some amount of dollars (say, x) in an interest bearing account and enter a forward contract to exchange x*(1 + i$) dollars for reais in July

• Let FBRL/$ be the forward exchange rate. • Then for the plan to succeed, x * (1 + i$) * FBRL/$ = BR 24000 that is, x = BRL 24000 / [(1 + i$) * FBRL/$ ]
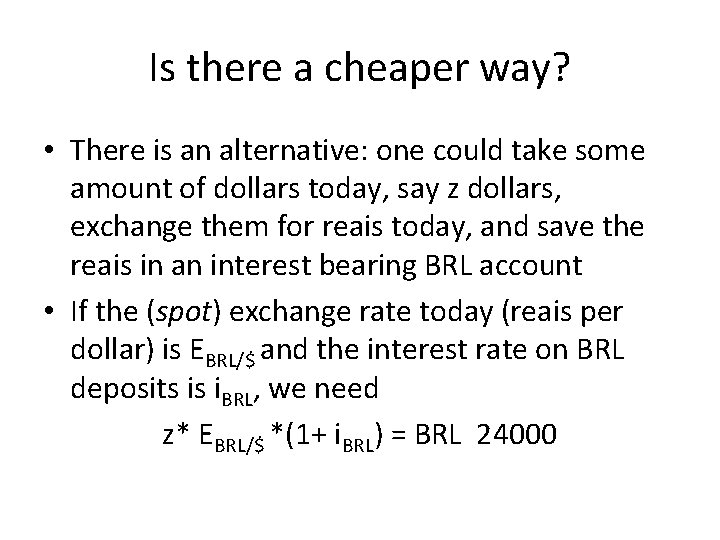
Is there a cheaper way? • There is an alternative: one could take some amount of dollars today, say z dollars, exchange them for reais today, and save the reais in an interest bearing BRL account • If the (spot) exchange rate today (reais per dollar) is EBRL/$ and the interest rate on BRL deposits is i. BRL, we need z* EBRL/$ *(1+ i. BRL) = BRL 24000

z* EBRL/$ *(1+ i. BRL) = BRL 24000 Or, equivalently, z = BRL 24000/[EBRL/$ *(1+ i. BRL) ]

There is no free lunch! • Summarizing, there are two ways to plan to have 24000 BRL by July: x = BRL 24000 / [(1 + i$) * FBRL/$ ] z = BRL 24000/[EBRL/$ *(1+ i. BRL) ] • But x and z must be equal!! • Why? Suppose x < z. Then by borrowing the BRL 24000, obtaining z dollars today, and investing x in dollars, one would make z – x instantly, at no cost, and without risk.

Implications of No Arbitrage • It follows that no arbitrage requires: x = BRL 24000 / [(1 + i$) * FBRL/$ ] = z = BRL 24000/[EBRL/$ *(1+ i. BRL) ] that is (1 + i$) * FBRL/$ = EBRL/$ *(1+ i. BRL) or FBRL/$ = EBRL/$ *(1+ i. BRL)/ (1 + i$)

Covered Interest Parity • The condition FBRL/$ = EBRL/$ *(1+ i. BRL)/ (1 + i$) is known as covered interest parity. As seen, it is an implication of no arbitrage. • This can be used to infer the forward exchange rate. Today, EBRL/$ = 2. 4, and (approximately) i$ = 0. 001, i. BRL = 0. 05025, so the forward rate should be: FBRL/$ = 2. 4* (1. 05025)/(1. 001) = 2. 52

Concepts • Exchange Rates: Spot and Forward • No Arbitrage • Interest Parity