GOALS of High School GEOMETRY MEASUREMENT Remember the

GOALS of High School GEOMETRY • MEASUREMENT Remember the Grade School Rules of how to MEASURE and add to/connect them • EXTENSION Learn the METHODS & LOGIC of Extending the Measurement Rules to New Ideas • ABSTRACTION Learn how to change geometric measurement problems to algebra problems and vice versa

GOALS of High School GEOMETRY • ABSTRACTION A group of seven weary men once arrived at a small hotel and asked for accommodations for the night, specifying that they wanted separate rooms. The manager admitted that he had only six rooms left, but thought he might be able to put up his guests as they desired. He took the first man to the first room and asked one of the other men to stay there for a few minutes. He then took the third man to the second room, the fourth man to the third room, the fifth man to the fourth room and the sixth man to the fifth room. Then he returned to the first room, got the seventh man, and showed him to the sixth room. Everyone was thus nicely taken care of. Or was he?

• Identify and model points, lines, and planes. • Identify collinear and coplanar points and intersecting lines and planes in space. • undefined term • plane • point • coplanar • line • space • collinear • locus • intersection

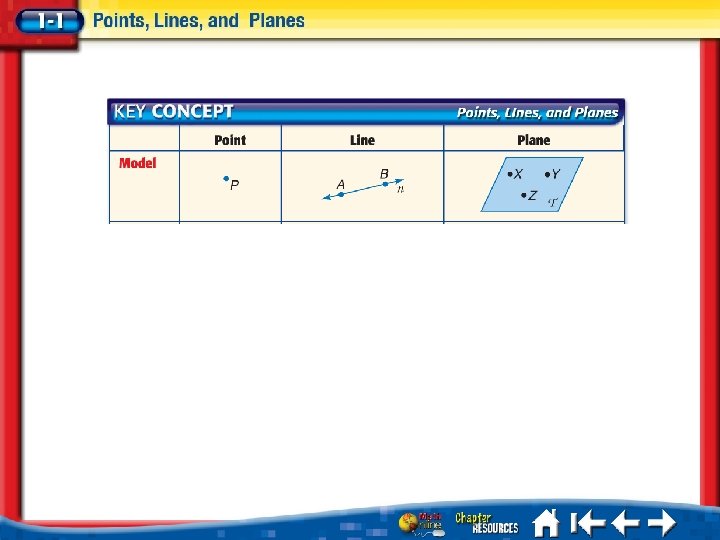
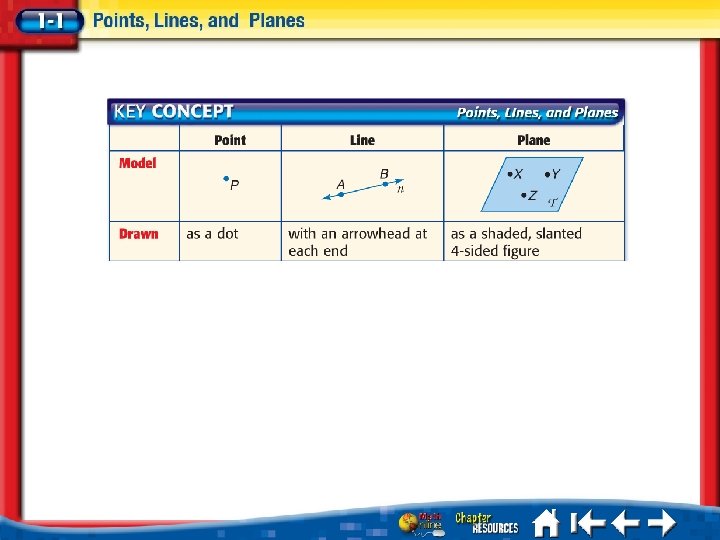
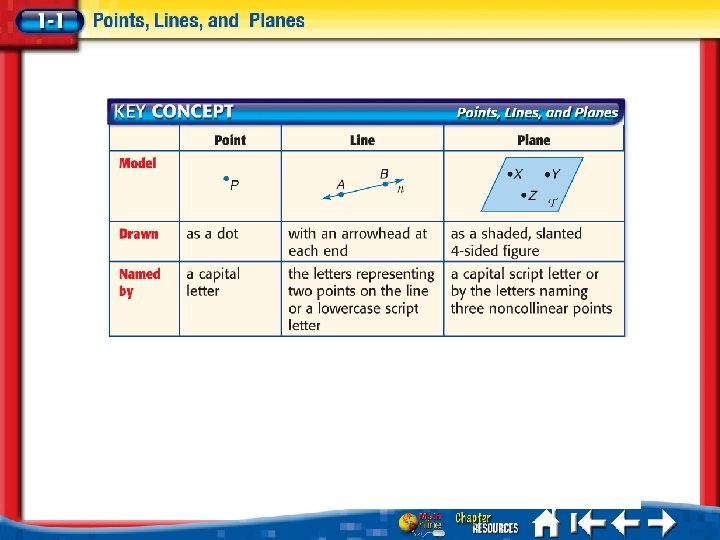
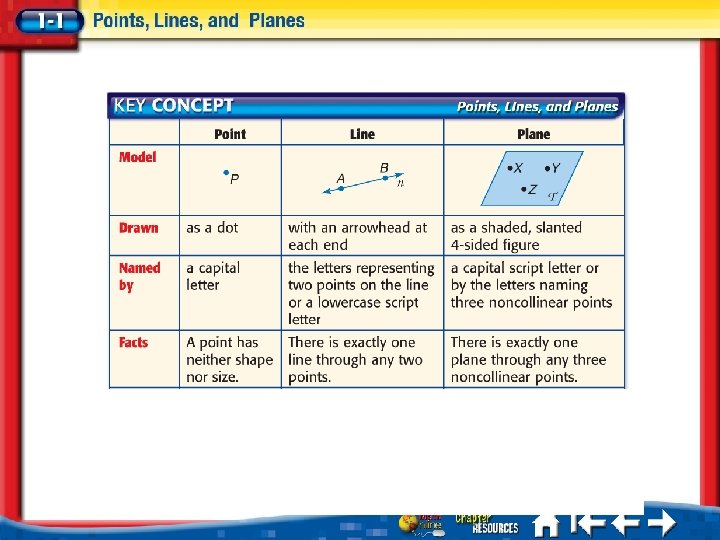
Undefined Terms – Words, usually readily understood, that are NOT formally explained by means of more basic words and concepts. The basic undefined terms of Geometry are point, line and plane. POINT – a location in space with NO LENGTH or WIDTH. LINE – an infinite set of points with INFINITE LENGTH, but NO WIDTH. PLANE – an infinite SET of points with INFINITE LENGTH, INFINITE WIDTH, but NO THICKNESS.

SPACE – The boundless 3 -dimensional set of of ALL POINTS. COLLINEAR – Points that lie on the SAME LINE. COPLANAR – Points that line in the SAME PLANE. LOCUS – The set of points that SATISFY a GIVEN CONDITION. INTERSECTION - the SET of POINTS that are CONTAINED in BOTH Figures

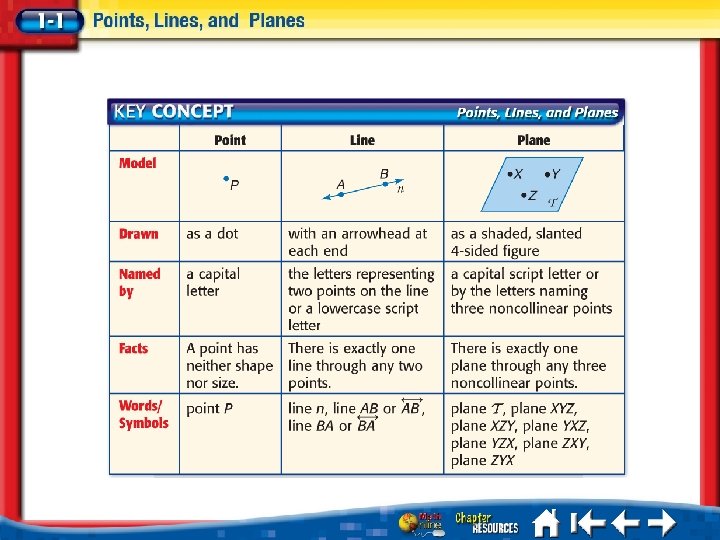
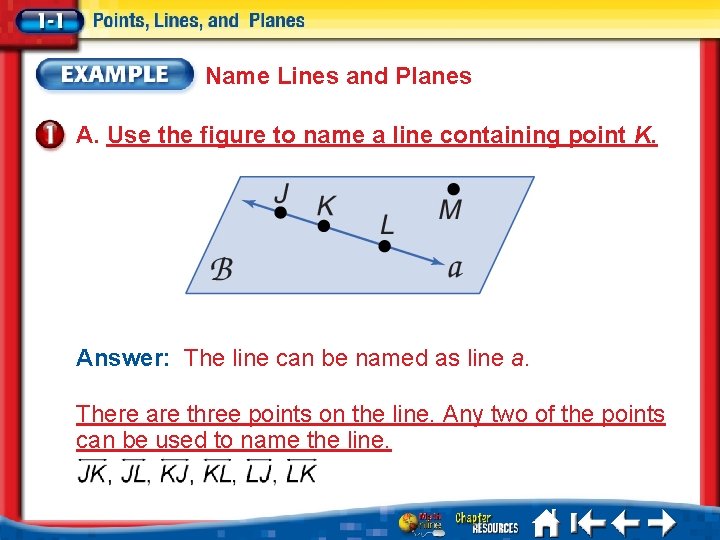
Name Lines and Planes A. Use the figure to name a line containing point K. Answer: The line can be named as line a. There are three points on the line. Any two of the points can be used to name the line.

Name Lines and Planes B. Use the figure to name a plane containing point L. Answer: The plane can be named as plane B. You can also use the letters of any three noncollinear points to name the plane JKM plane KLM plane JLM

Name Lines and Planes The letters of each of these names can be reordered to create other acceptable names for this plane. For example, JKM can also be written as JMK, MKJ, KJM, KMJ, and MJK. There are 15 different three-letter names for this plane.

A. Use the figure to name a line containing the point X. A. line X B. line c C. line Z D. A. B. C. D. A B C D

B. Use the figure to name a plane containing point Z. A. plane XY B. plane c C. plane XQY D. plane P A. B. C. D. A B C D

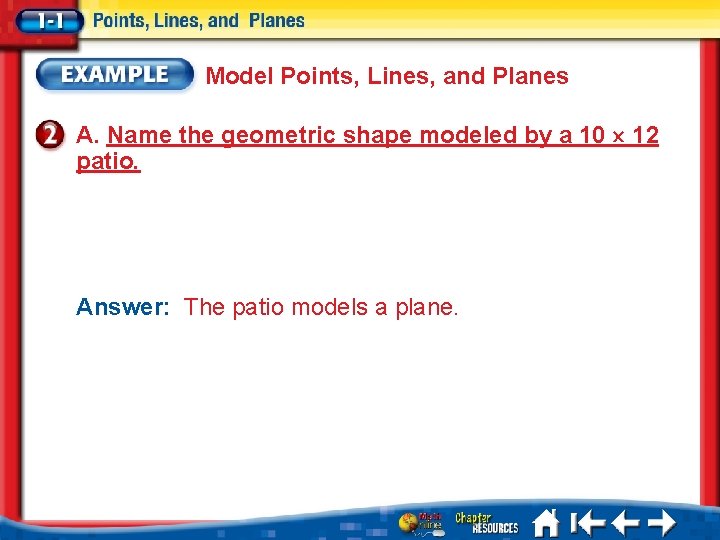
Model Points, Lines, and Planes A. Name the geometric shape modeled by a 10 12 patio. Answer: The patio models a plane.

Model Points, Lines, and Planes B. Name the geometric shape modeled by a drop of water on a table. Answer: The drop on the table models a point on a plane.

A. VISUALIZATION Name the geometric shape modeled by a colored dot on a map used to mark the location of a city. A. point B. line segment C. plane D. none of the above 1. 2. 3. 4. A B C D

B. VISUALIZATION Name the geometric shape modeled by the ceiling of your classroom. A. point B. line segment C. plane D. none of the above 1. 2. 3. 4. A B C D

Draw Geometric Figures Draw a surface to represent plane R and label it.

Draw Geometric Figures Draw a line anywhere on the plane.

Draw Geometric Figures Draw dots on the line for point A and B. Label the points.

Draw Geometric Figures

Draw Geometric Figures Draw dots on this line for point D and E. Label the points.

Draw Geometric Figures Label the intersection point of the two lines as P.

Draw Geometric Figures Answer:

Draw Geometric Figures Answer: There an infinite number of points that are collinear with Q and R. In the graph, one such point is T(1, 0).

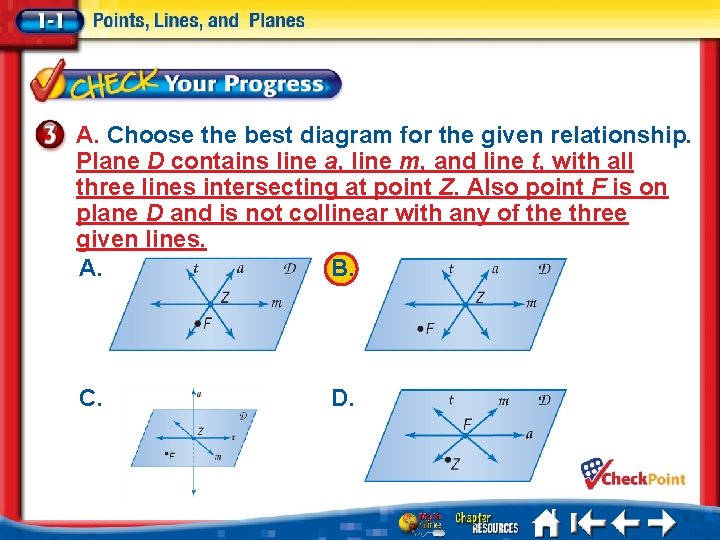
A. Choose the best diagram for the given relationship. Plane D contains line a, line m, and line t, with all three lines intersecting at point Z. Also point F is on plane D and is not collinear with any of the three given lines. A. B. C. D. 1. 2. 3. 4. A B C D

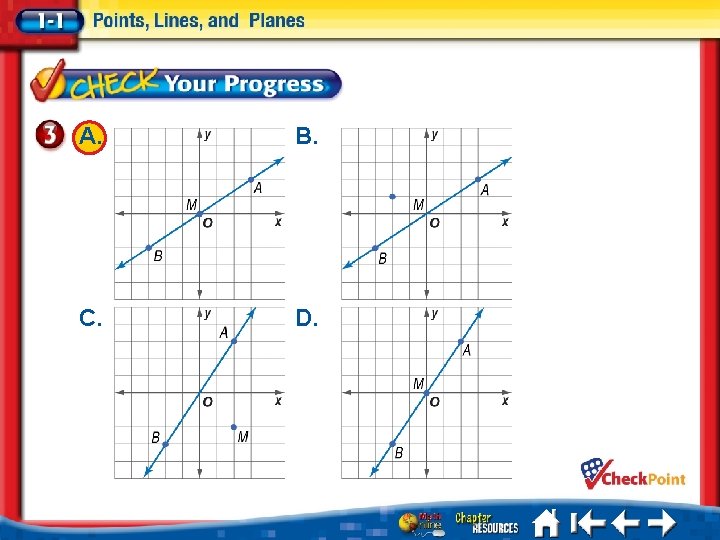
A. B. C. D. 1. 2. 3. 4. A B C D

Interpret Drawings A. How many planes appear in this figure? Answer: There are two planes: plane S and plane ABC.

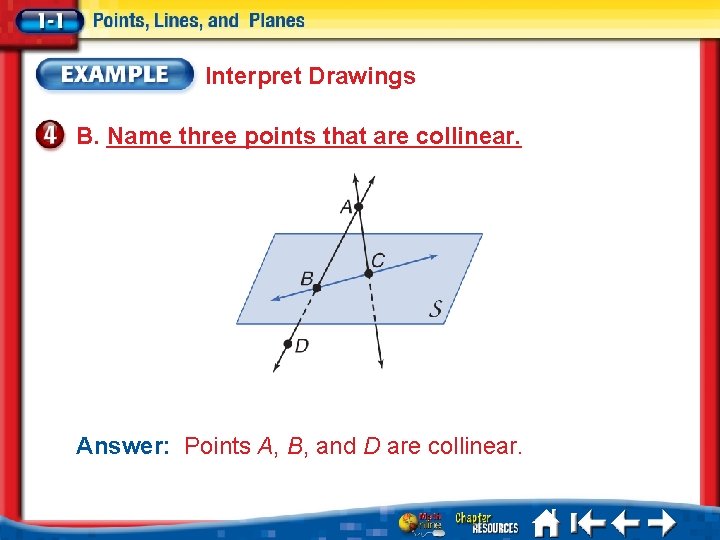
Interpret Drawings B. Name three points that are collinear. Answer: Points A, B, and D are collinear.

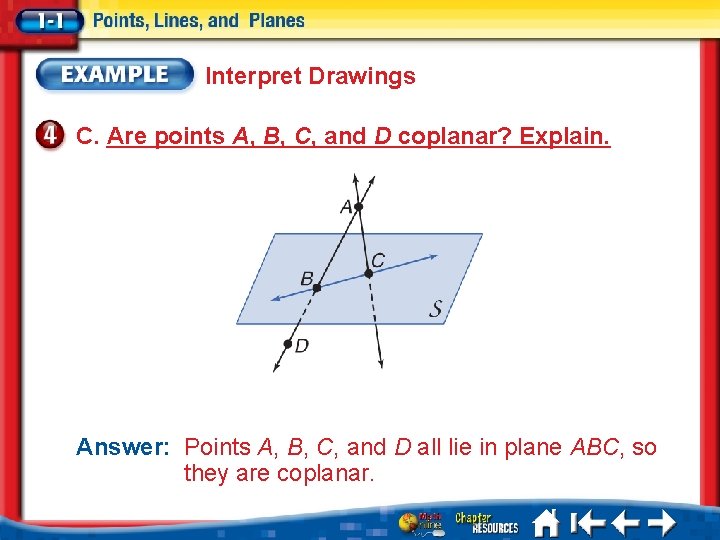
Interpret Drawings C. Are points A, B, C, and D coplanar? Explain. Answer: Points A, B, C, and D all lie in plane ABC, so they are coplanar.

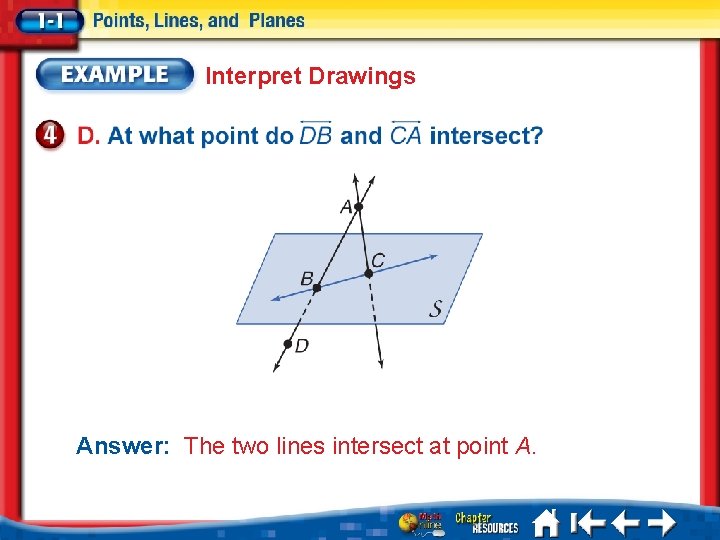
Interpret Drawings Answer: The two lines intersect at point A.

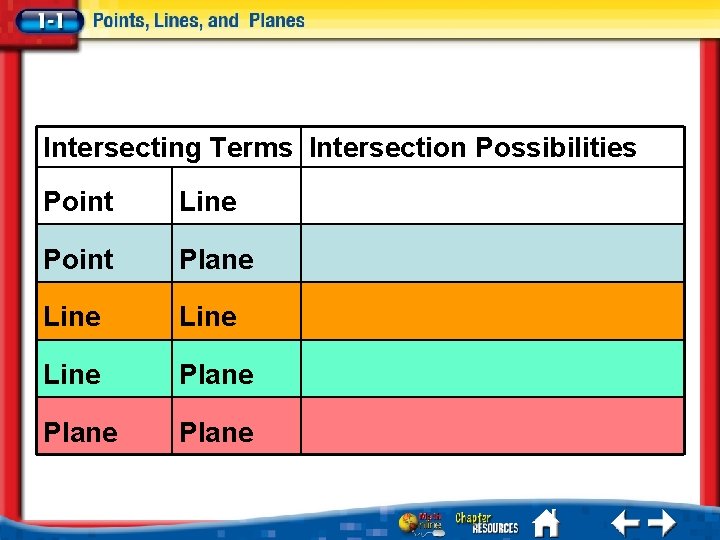
Intersecting Terms Intersection Possibilities Point Line Point Plane Line Plane

A. How many planes appear in this figure? A. one B. two C. three D. four A. B. C. D. A B C D

B. Name three points that are collinear. A. B, O, and X B. X, O, and N C. R, O, and B D. A, X, and Z A. B. C. D. A B C D

C. Are point X, O, and R coplanar? A. yes B. no C. cannot be determined 1. 2. 3. A B C

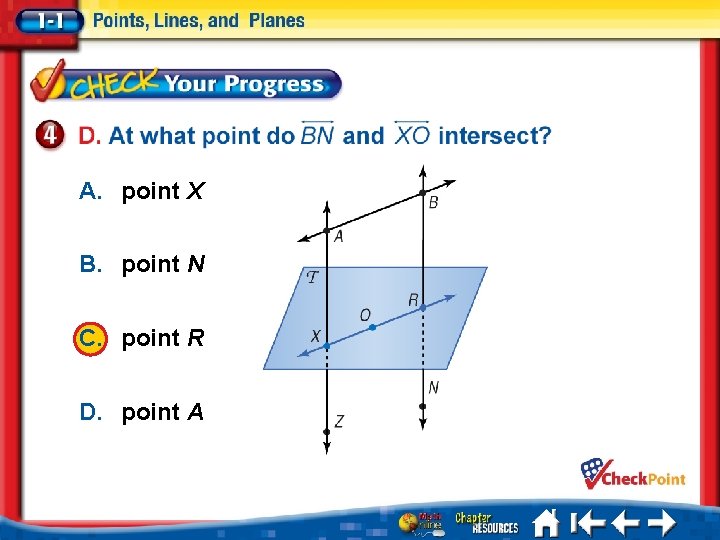
A. point X B. point N C. point R D. point A A. B. C. D. A B C D

You should be able to: DEFINE the BIG Three Undefined Terms DESCRIBE the Attributes of each Undefined Term DESCRIBE the resulting INTERSECTION of Undefined Terms as a point, line or plane DETERMINE how many COLLINEAR points are needed to define a Line and a Plane

Five-Minute Checks Image Bank Math Tools Animation Menu Archeology and the Coordinate Plane

Lesson 1 -1 Lesson 1 -2 (over Lesson 1 -1) Lesson 1 -3 (over Lesson 1 -2) Lesson 1 -4 (over Lesson 1 -3) Lesson 1 -5 (over Lesson 1 -4) Lesson 1 -6 (over Lesson 1 -5) Lesson 1 -7 (over Lesson 1 -6)

To use the images that are on the following three slides in your own presentation: 1. Exit this presentation. 2. Open a chapter presentation using a full installation of Microsoft® Power. Point® in editing mode and scroll to the Image Bank slides. 3. Select an image, copy it, and paste it into your presentation.

1 -4 -1 Using a Protractor to Measure Three Types of Angles 1 -4 -2 Copy an Angle 1 -4 -3 Bisect an Angle 1 -5 Constructing Perpendiculars 1 -7 Orthographic Drawings

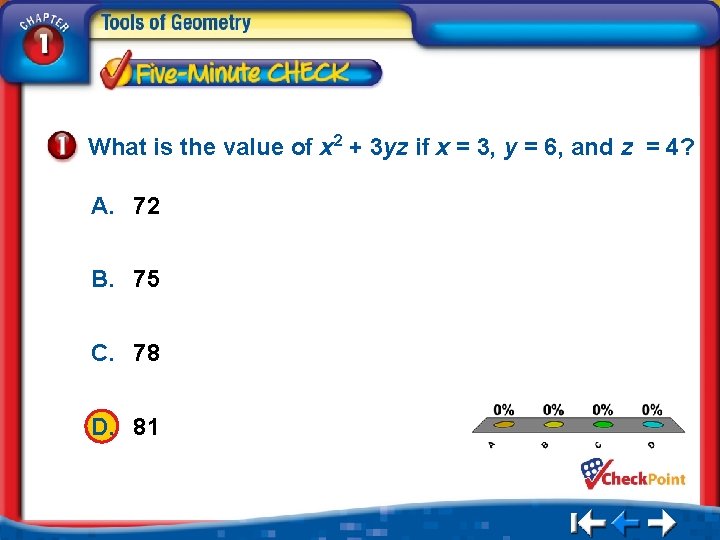
What is the value of x 2 + 3 yz if x = 3, y = 6, and z = 4? A. 72 B. 75 C. 78 D. 81 A. B. C. D. A B C D

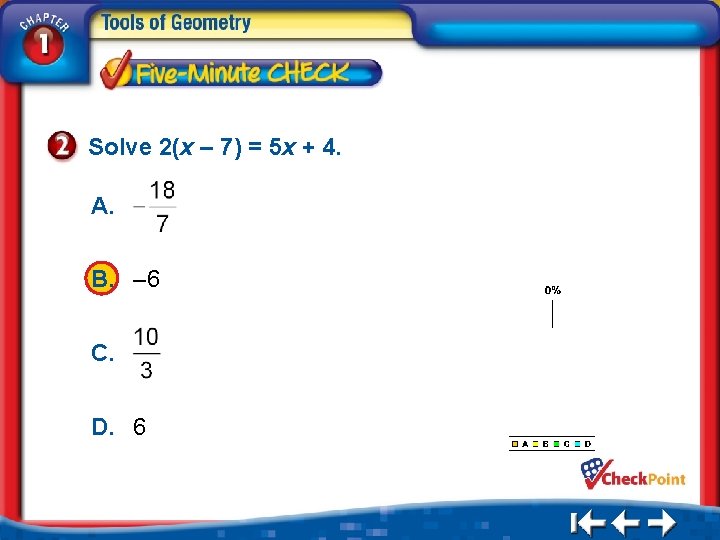
Solve 2(x – 7) = 5 x + 4. A. B. – 6 C. D. 6 1. 2. 3. 4. A B C D

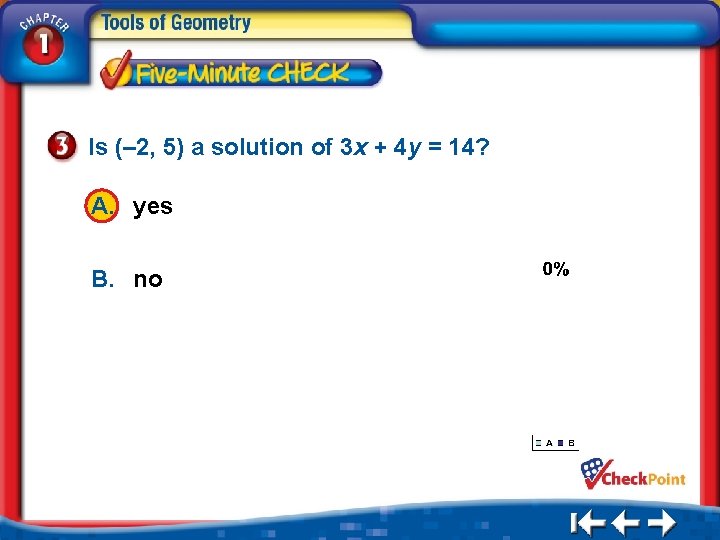
Is (– 2, 5) a solution of 3 x + 4 y = 14? A. yes B. no 1. A 2. B

Factor 9 x 2 – 25 y 2. A. (3 x + 5 y)2 B. 3 x 2 + 5 y 2 C. (3 x – 5 y)2 D. (3 x + 5 y)(3 x – 5 y) A. B. C. D. A B C D

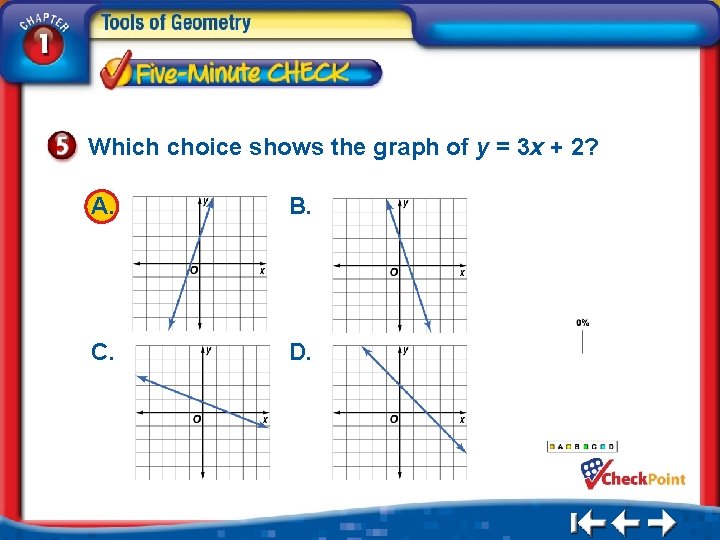
Which choice shows the graph of y = 3 x + 2? A. C. B. D. 1. 2. 3. 4. A B C D

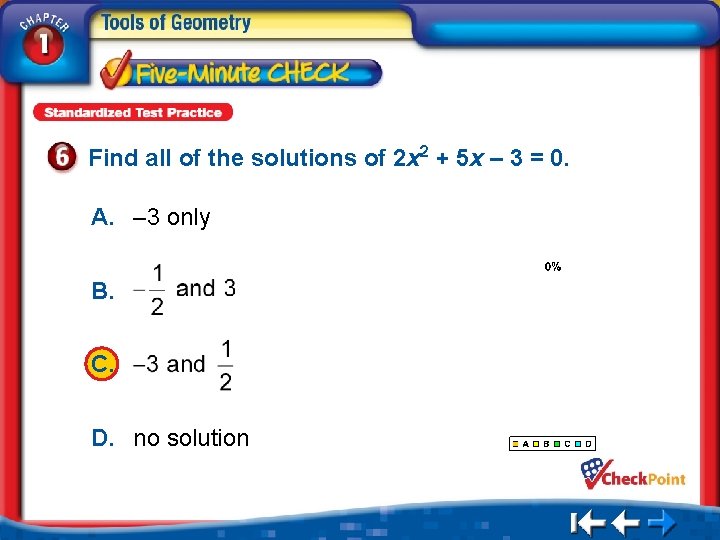
Find all of the solutions of 2 x 2 + 5 x – 3 = 0. A. – 3 only B. C. D. no solution 1. 2. 3. 4. A B C D

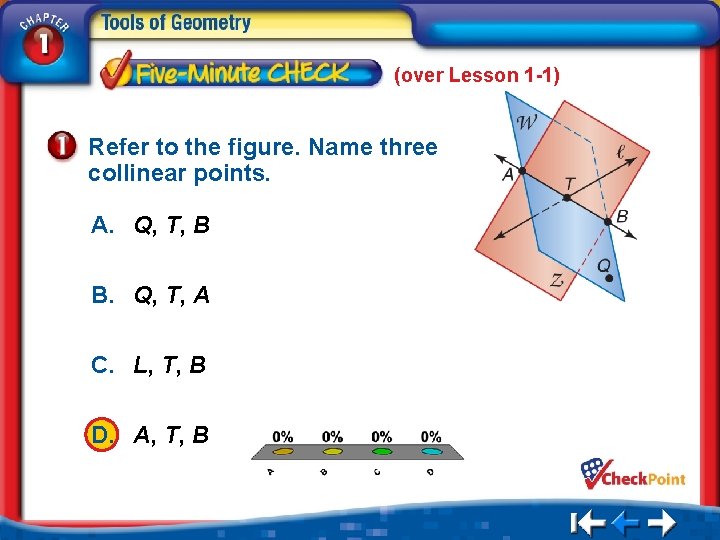
(over Lesson 1 -1) Refer to the figure. Name three collinear points. A. Q, T, B B. Q, T, A C. L, T, B D. A, T, B A. B. C. D. A B C D

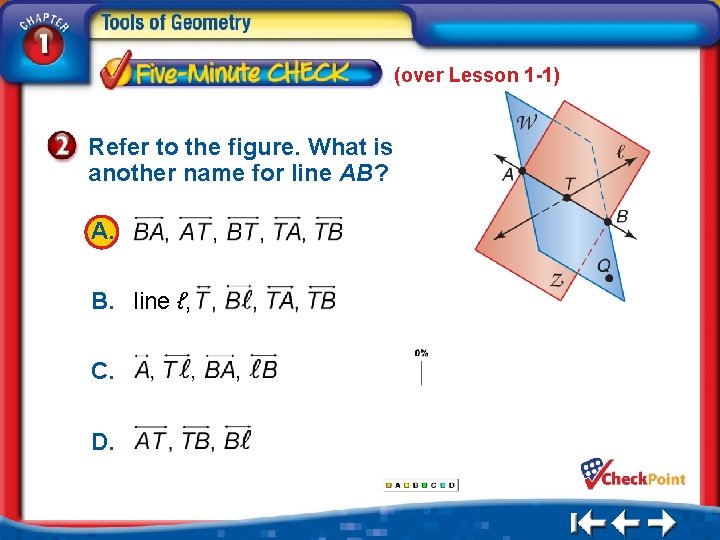
(over Lesson 1 -1) Refer to the figure. What is another name for line AB? A. B. line ℓ, C. D. 1. 2. 3. 4. A B C D

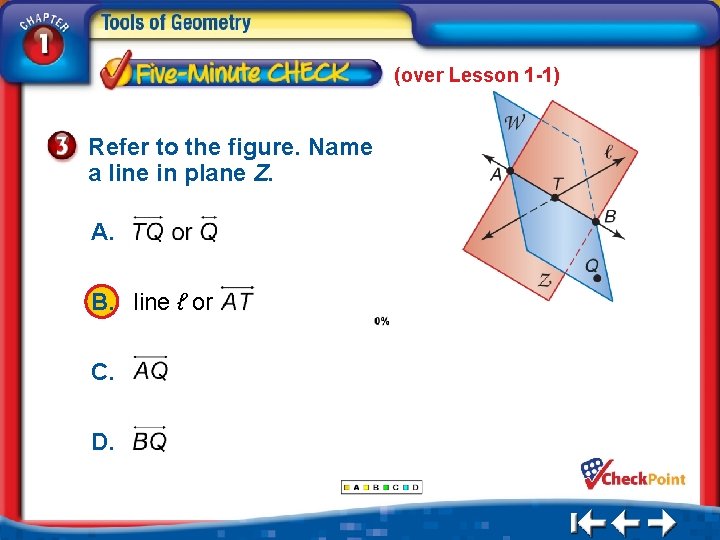
(over Lesson 1 -1) Refer to the figure. Name a line in plane Z. A. B. line ℓ or C. D. 1. 2. 3. 4. A B C D

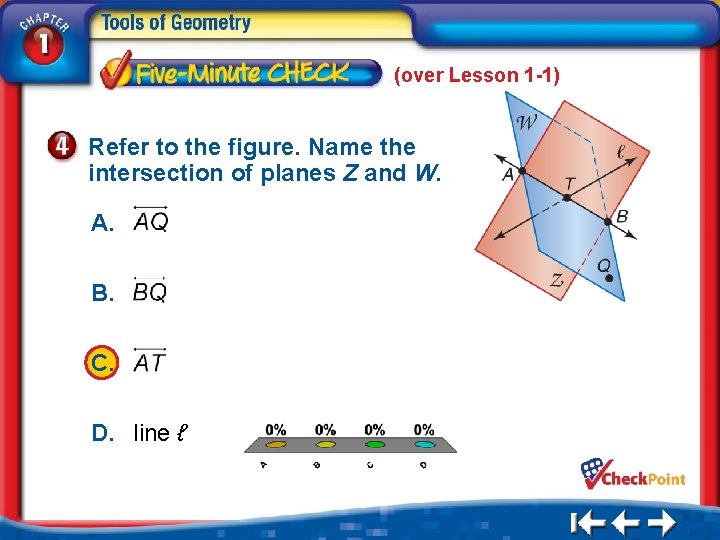
(over Lesson 1 -1) Refer to the figure. Name the intersection of planes Z and W. A. B. C. D. line ℓ A. B. C. D. A B C D

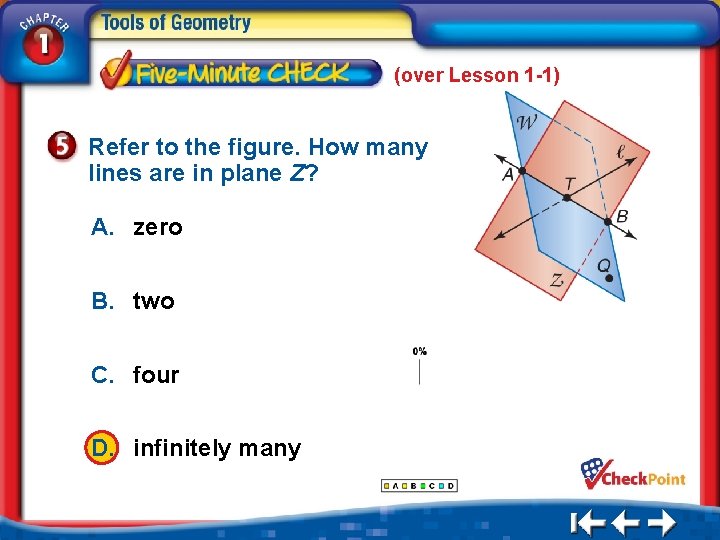
(over Lesson 1 -1) Refer to the figure. How many lines are in plane Z? A. zero B. two C. four D. infinitely many 1. 2. 3. 4. A B C D

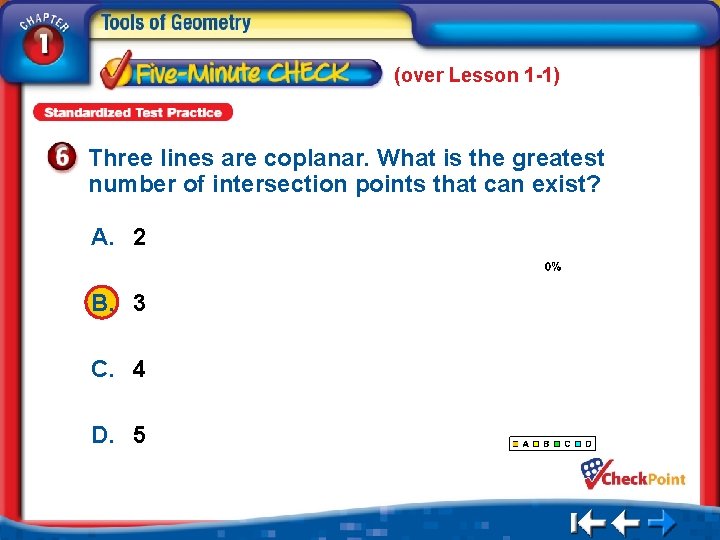
(over Lesson 1 -1) Three lines are coplanar. What is the greatest number of intersection points that can exist? A. 2 B. 3 C. 4 D. 5 1. 2. 3. 4. A B C D

(over Lesson 1 -2) Find the precision for a measurement of 42 centimeters. A. 40. 25 cm to 41. 75 cm B. 41 cm to 43 cm C. 41. 5 cm to 42. 5 cm D. 41. 75 cm to 42. 75 cm A. B. C. D. A B C D

(over Lesson 1 -2) If M is between L and N, LN = 3 x – 1, LM = 4, and MN = x – 1, find x and MN. A. x = 2, MN = 5 B. x = 2, MN = 1 C. x = 5, MN =4 D. x = 1. 5, MN = 0. 5 1. 2. 3. 4. A B C D

(over Lesson 1 -2) Use the figure to find RT. A. B. C. D. 1. 2. 3. 4. A B C D

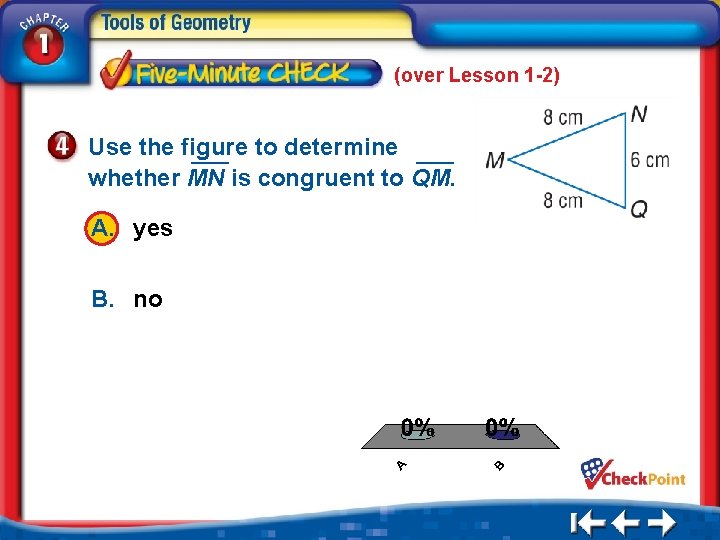
(over Lesson 1 -2) Use the figure to determine whether MN is congruent to QM. A. yes B. no A. A B. B

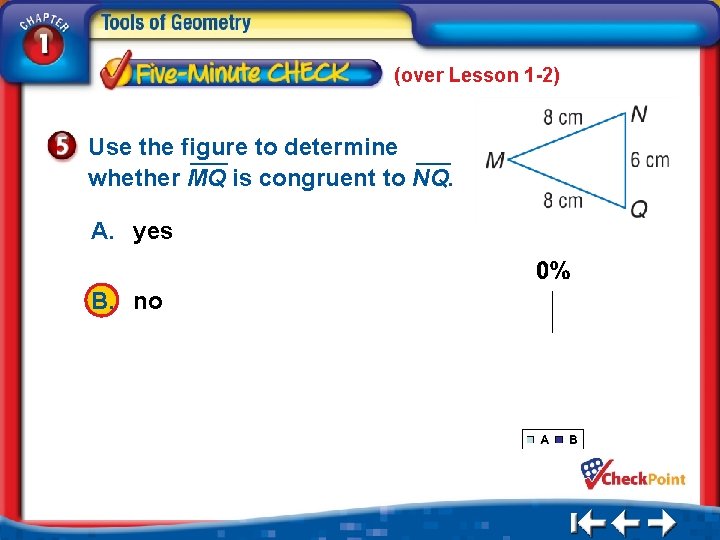
(over Lesson 1 -2) Use the figure to determine whether MQ is congruent to NQ. A. yes B. no 1. A 2. B

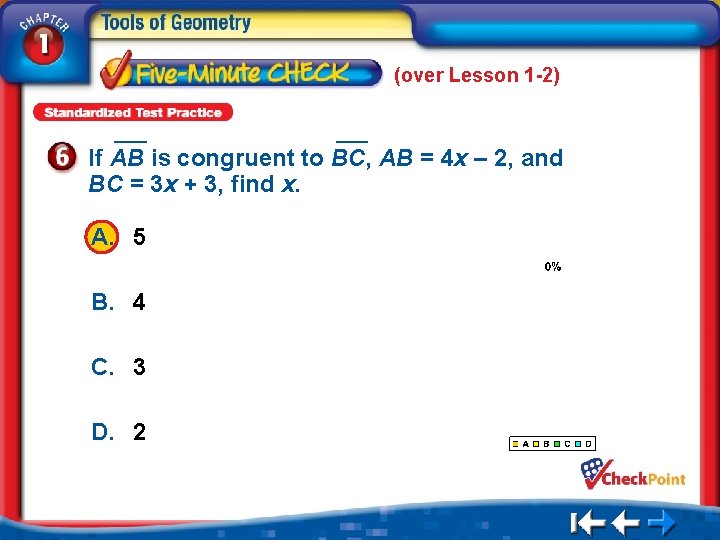
(over Lesson 1 -2) If AB is congruent to BC, AB = 4 x – 2, and BC = 3 x + 3, find x. A. 5 B. 4 C. 3 D. 2 1. 2. 3. 4. A B C D

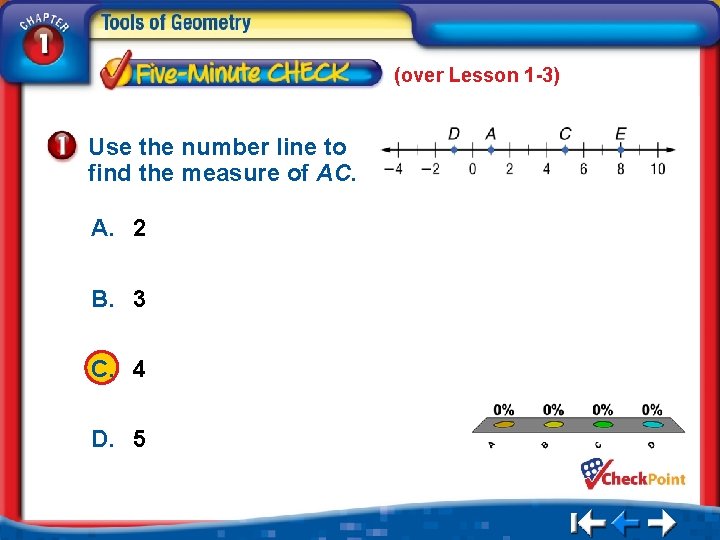
(over Lesson 1 -3) Use the number line to find the measure of AC. A. 2 B. 3 C. 4 D. 5 A. B. C. D. A B C D

(over Lesson 1 -3) Use the number line to find the measure of DE. A. 9 B. 8. 5 C. 8 D. 7 1. 2. 3. 4. A B C D

(over Lesson 1 -3) Use the number line to find the midpoint of EG. A. E B. F C. G D. H 1. 2. 3. 4. A B C D

(over Lesson 1 -3) Find the distance between P(– 2, 5) and Q(4, – 3). A. 10 B. 8. 12 C. 9 D. 6. 32 A. B. C. D. A B C D

(over Lesson 1 -3) Find the coordinates of R if M(– 4, 5) is the midpoint of RS and S has coordinates (0, – 10). A. (8, 20) B. (8, – 20) C. (– 8, 20) D. (– 8, 0) 1. 2. 3. 4. A B C D

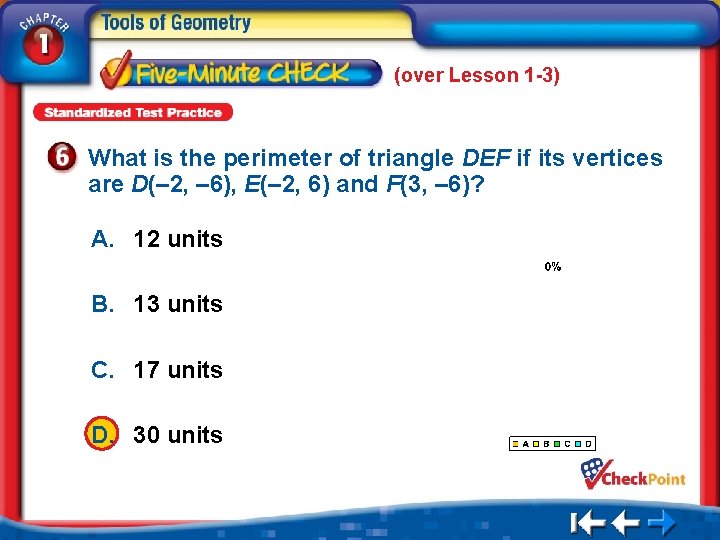
(over Lesson 1 -3) What is the perimeter of triangle DEF if its vertices are D(– 2, – 6), E(– 2, 6) and F(3, – 6)? A. 12 units B. 13 units C. 17 units D. 30 units 1. 2. 3. 4. A B C D

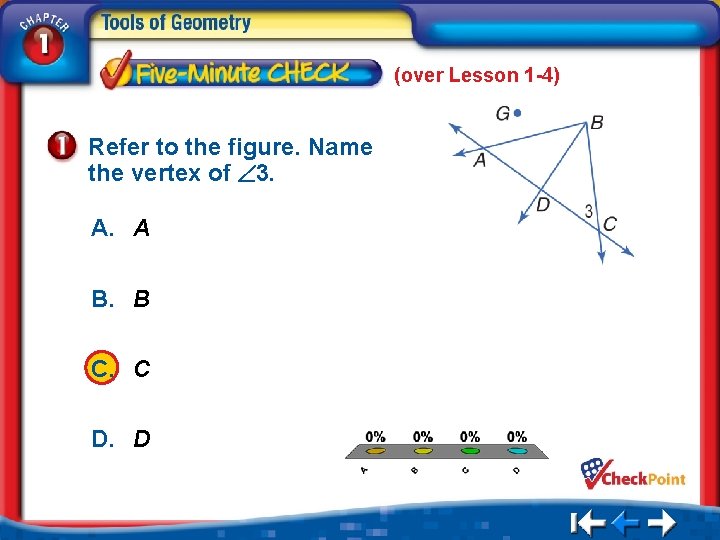
(over Lesson 1 -4) Refer to the figure. Name the vertex of 3. A. A B. B C. C D. D A. B. C. D. A B C D

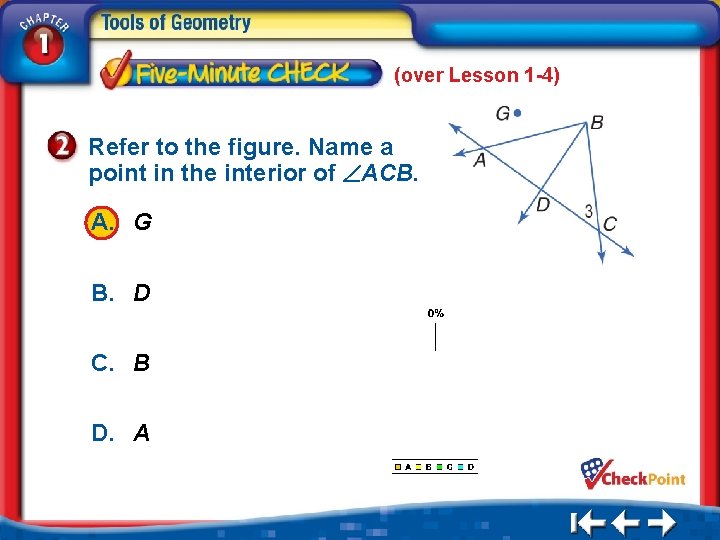
(over Lesson 1 -4) Refer to the figure. Name a point in the interior of ACB. A. G B. D C. B D. A 1. 2. 3. 4. A B C D

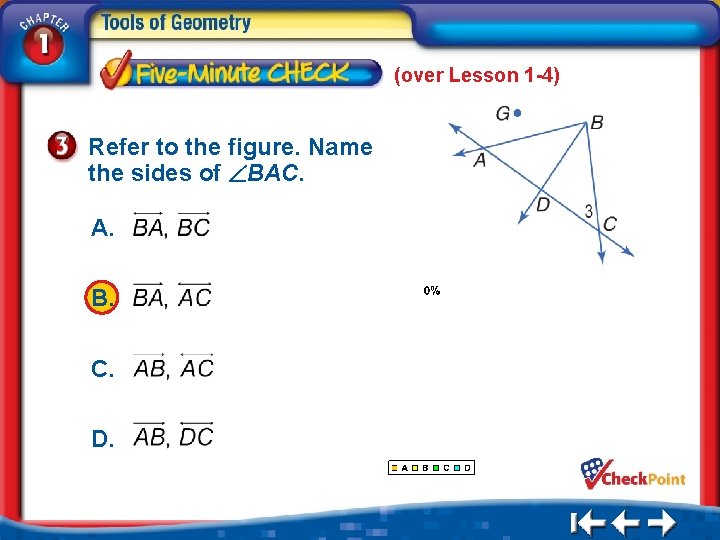
(over Lesson 1 -4) Refer to the figure. Name the sides of BAC. A. B. C. D. 1. 2. 3. 4. A B C D

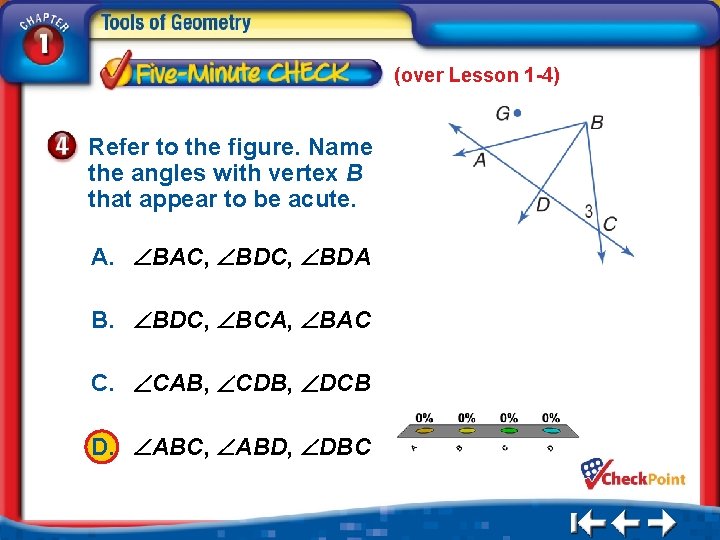
(over Lesson 1 -4) Refer to the figure. Name the angles with vertex B that appear to be acute. A. BAC, BDA B. BDC, BCA, BAC C. CAB, CDB, DCB D. ABC, ABD, DBC A. B. C. D. A B C D

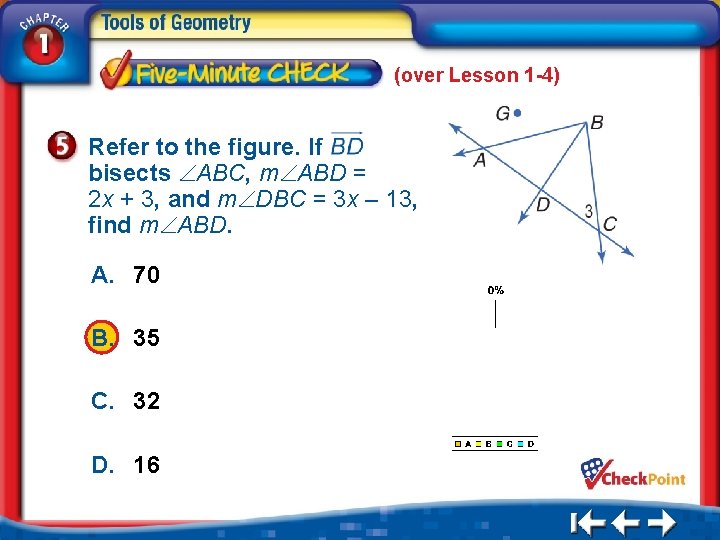
(over Lesson 1 -4) Refer to the figure. If bisects ABC, m ABD = 2 x + 3, and m DBC = 3 x – 13, find m ABD. A. 70 B. 35 C. 32 D. 16 1. 2. 3. 4. A B C D

(over Lesson 1 -4) If P is in the interior of MON and m MOP = m MON, what can you conclude? A. PON NOM B. MON is an acute angle. C. D. m MOP > m PON 1. 2. 3. 4. A B C D

(over Lesson 1 -5) Refer to the figure. Name two acute vertical angles. A. AEB and AED B. AED and BEC C. DEC and CEB D. AEB and DEC A. B. C. D. A B C D

(over Lesson 1 -5) Refer to the figure. Name a linear pair whose vertex is E. A. AEB, DEC B. AEB, AED C. AED, BEC D. CED, BEA 1. 2. 3. 4. A B C D

(over Lesson 1 -5) Refer to the figure. Name an angle supplementary to BEC. A. CED B. DEA C. AED D. AEC 1. 2. 3. 4. A B C D

(over Lesson 1 -5) 1 and 2 are a pair of supplementary angles, and the measure of 1 is twice the measure of 2. Find the measures of both angles. A. m 1 = 60, m 2 = 120 B. m 1 = 30, m 2 = 60 C. m 1 = 120, m 2 = 60 D. m 1 = 60, m 2 = 30 A. B. C. D. A B C D

(over Lesson 1 -5) If RS is perpendicular to ST and is the angle bisector of RST, what is m TSV? A. 180 B. 90 C. 60 D. 45 1. 2. 3. 4. A B C D

(over Lesson 1 -5) If two angles are both congruent and supplementary, they must be ? . A. two right angles B. two acute angles C. two obtuse angles D. an obtuse and an acute angle 1. 2. 3. 4. A B C D

(over Lesson 1 -6) Name polygon A by its number of sides. A. pentagon B. nonagon C. heptagon D. octagon A. B. C. D. A B C D

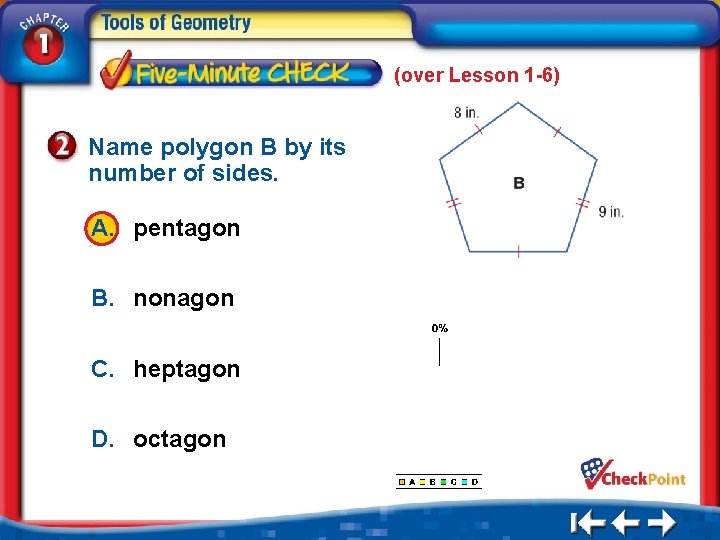
(over Lesson 1 -6) Name polygon B by its number of sides. A. pentagon B. nonagon C. heptagon D. octagon 1. 2. 3. 4. A B C D

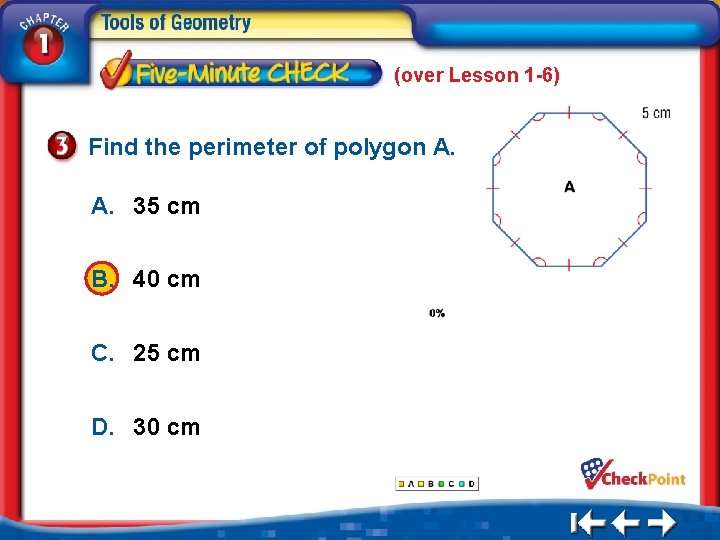
(over Lesson 1 -6) Find the perimeter of polygon A. A. 35 cm B. 40 cm C. 25 cm D. 30 cm 1. 2. 3. 4. A B C D

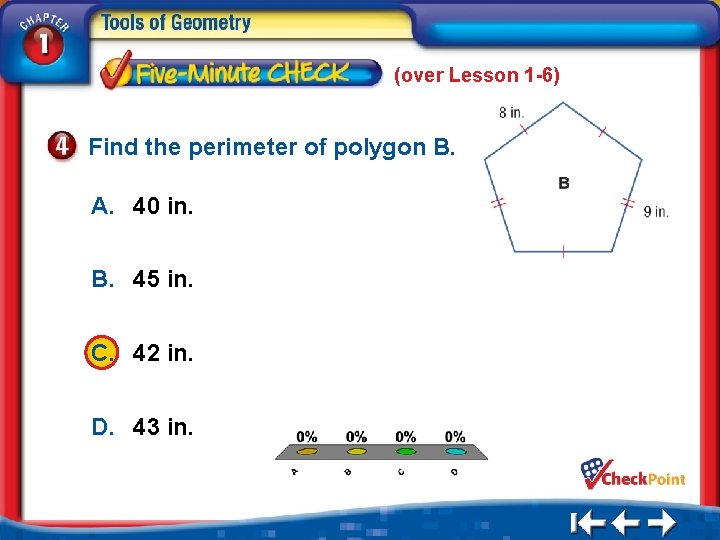
(over Lesson 1 -6) Find the perimeter of polygon B. A. 40 in. B. 45 in. C. 42 in. D. 43 in. A. B. C. D. A B C D

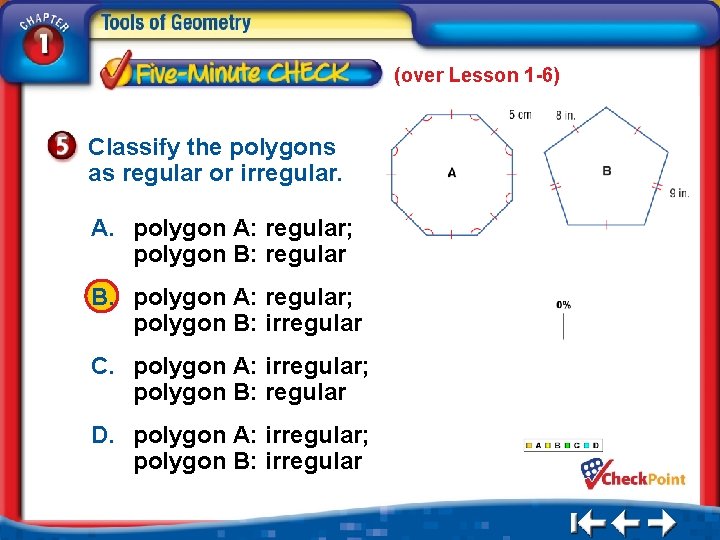
(over Lesson 1 -6) Classify the polygons as regular or irregular. A. polygon A: regular; polygon B: regular B. polygon A: regular; polygon B: irregular C. polygon A: irregular; polygon B: regular D. polygon A: irregular; polygon B: irregular 1. 2. 3. 4. A B C D

(over Lesson 1 -6) What is the area of rectangle FGHJ if its vertices are F(– 3, 2), G(4, 2), H(4, – 3), and J(– 3, – 3)? A. 24 square units B. 35 square units C. 49 square units D. 25 square units 1. 2. 3. 4. A B C D

This slide is intentionally blank.