Goals Global Volumetric Parameterization Arbitrary Topology Complex Geometry

Goals • Global Volumetric Parameterization – Arbitrary Topology – Complex Geometry – Automatically ( Semi-Automatically) – Less Segments – Seamless – Low Distortion • Trivariate Spline – No Trimming – Global Continuity
![Applications • • Mapping [He et al. SMI 2009] [Li et al. SPM 2007] Applications • • Mapping [He et al. SMI 2009] [Li et al. SPM 2007]](http://slidetodoc.com/presentation_image/4b7f170b147cdaeab00f151c7ccf9d9b/image-2.jpg)
Applications • • Mapping [He et al. SMI 2009] [Li et al. SPM 2007] Texturing [Zhang et al. CMAME 2007] Isogeometric Analysis More [Courtesy of He et al. SMI 2009] [Courtesy of Li et al. SPM 2007] [Courtesy of Zhang et al. CMAME 2007]

Motivation • Challenge 1 : How to parameterize the model with – High Topology – Complex Geometry • Solution: Segmentation • Challenge 2: How to construct the domain: – Less Segments – Shape Aligned – General Representation
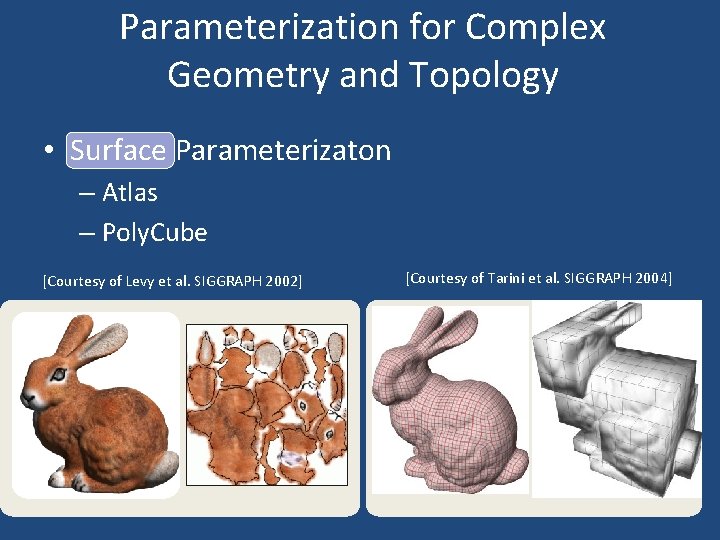
Parameterization for Complex Geometry and Topology • Surface Parameterizaton – Atlas – Poly. Cube [Courtesy of Levy et al. SIGGRAPH 2002] [Courtesy of Tarini et al. SIGGRAPH 2004]
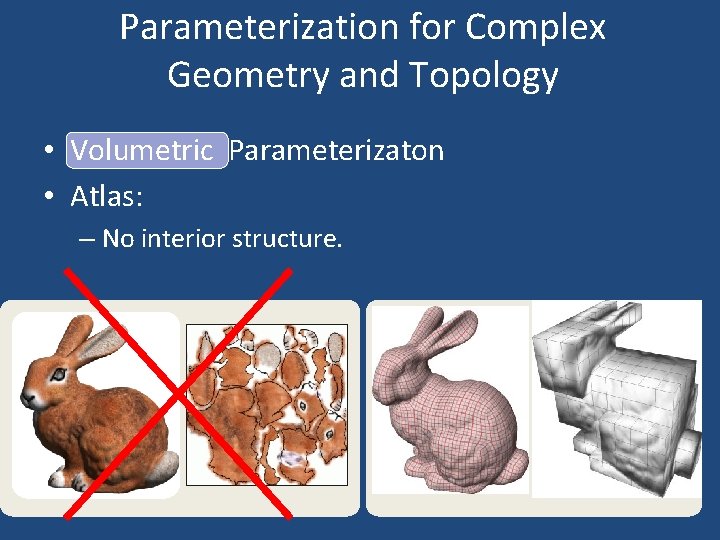
Parameterization for Complex Geometry and Topology • Volumetric Parameterizaton • Atlas: – No interior structure.

Poly. Cube: Pros • Simple structure and local regularity • Flexible and simple connectivity [Courtesy of Tarini et al. SIGGRAPH 2004] • Avoid singularity
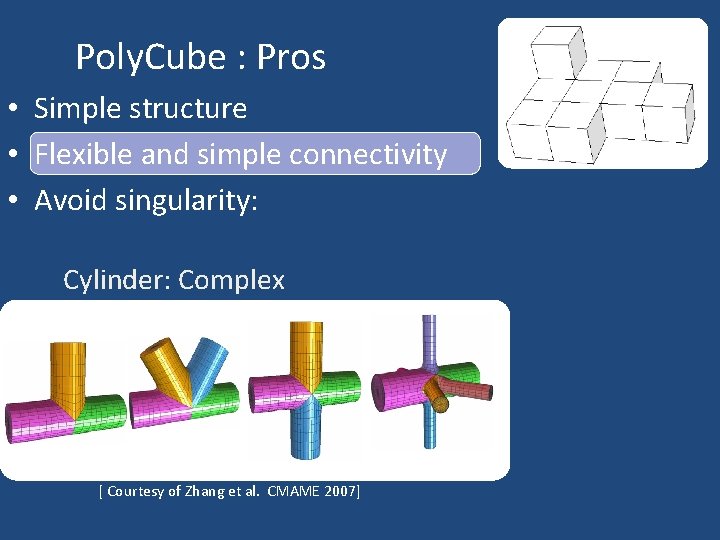
Poly. Cube : Pros • Simple structure • Flexible and simple connectivity • Avoid singularity: Cylinder: Complex [ Courtesy of Zhang et al. CMAME 2007]
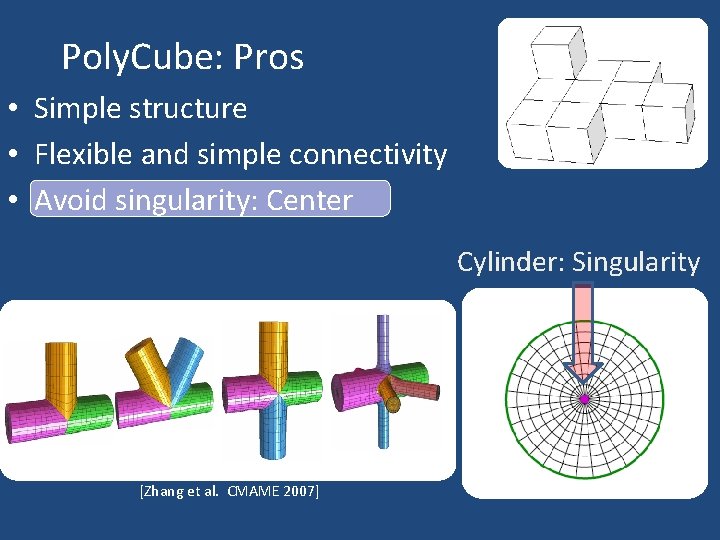
Poly. Cube: Pros • Simple structure • Flexible and simple connectivity • Avoid singularity: Center Cylinder: Singularity [Zhang et al. CMAME 2007]
![Previous Work on Poly. Cube • Manually [Courtesy of Tarini et al. Siggraph 2004] Previous Work on Poly. Cube • Manually [Courtesy of Tarini et al. Siggraph 2004]](http://slidetodoc.com/presentation_image/4b7f170b147cdaeab00f151c7ccf9d9b/image-9.jpg)
Previous Work on Poly. Cube • Manually [Courtesy of Tarini et al. Siggraph 2004] • Automatically – Skeleton-Based – Axis-Aligned Scanning [Courtesy of Lin et al. GMP 2008] [Courtesy of He et al. SMI 2009]

Motivation • Challenge 1 : How to parameterize the model with – High Topology – Complex Geometry • Solution: Segmentation • Challenge 2: How to construct the Poly. Cube domain (for better splines): – Less Segments – Shape Aligned – General Representation
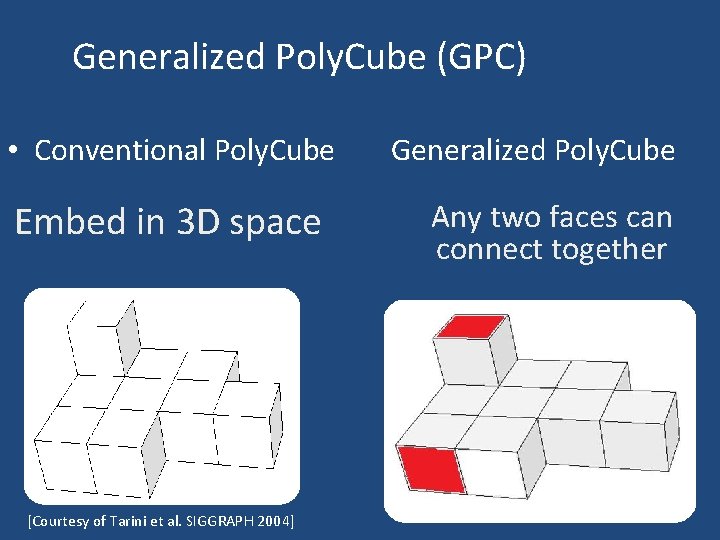
Generalized Poly. Cube (GPC) • Conventional Poly. Cube Embed in 3 D space [Courtesy of Tarini et al. SIGGRAPH 2004] Generalized Poly. Cube Any two faces can connect together
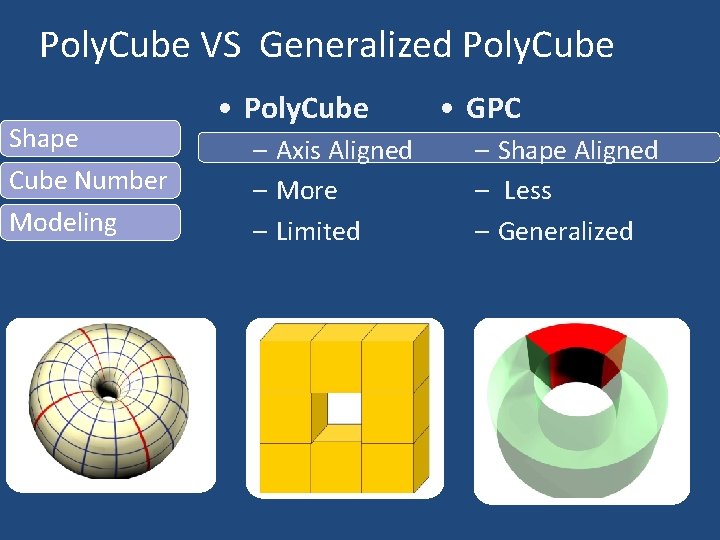
Poly. Cube VS Generalized Poly. Cube Shape Cube Number Modeling • Poly. Cube – Axis Aligned – More – Limited • GPC – Shape Aligned – Less – Generalized
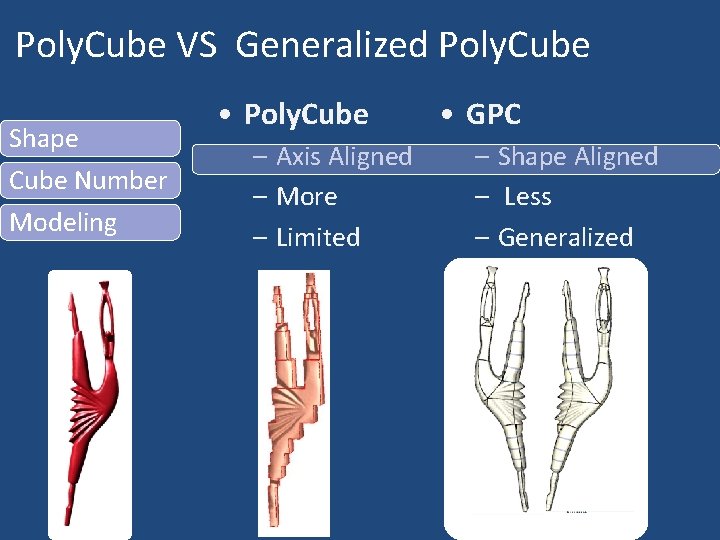
Poly. Cube VS Generalized Poly. Cube Shape Cube Number Modeling • Poly. Cube – Axis Aligned – More – Limited • GPC – Shape Aligned – Less – Generalized
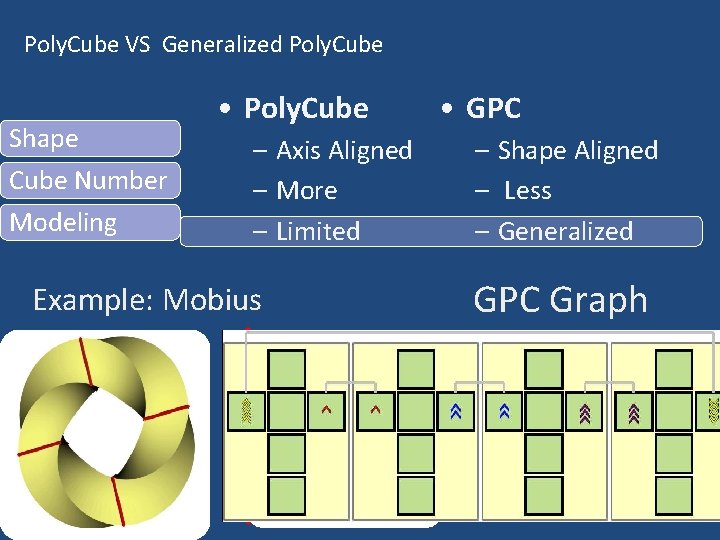
Poly. Cube VS Generalized Poly. Cube Shape Cube Number Modeling • Poly. Cube – Axis Aligned – More – Limited Example: Mobius • GPC – Shape Aligned – Less – Generalized GPC Graph

Contributions • Efficient GPC Parameterization – GPC Representation via Generalized Cube Gluing – Decompose arbitrary model to cubes automatically – Glue Cubes to GPC consistently – Volumetric Cube Parameterization • Volumetric T-splines – Poly. Cube Domain to GPC Domain – Recursive Adaptive Fitting – Octree -based High Efficient Knot Vector Computation
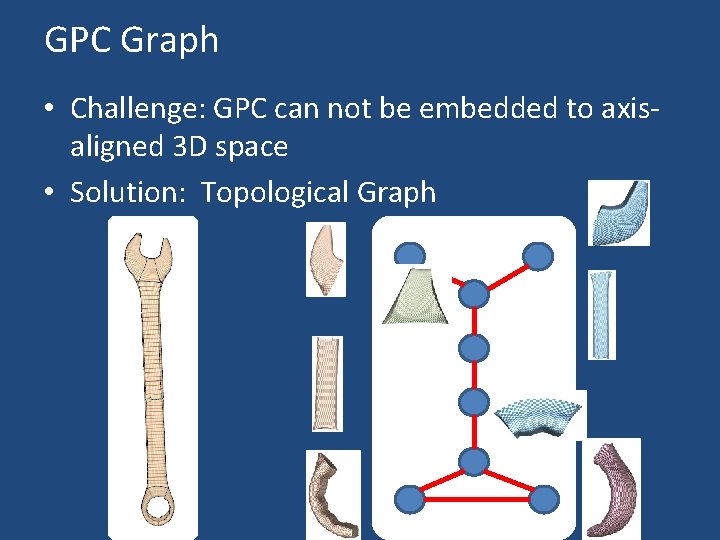
GPC Graph • Challenge: GPC can not be embedded to axisaligned 3 D space • Solution: Topological Graph
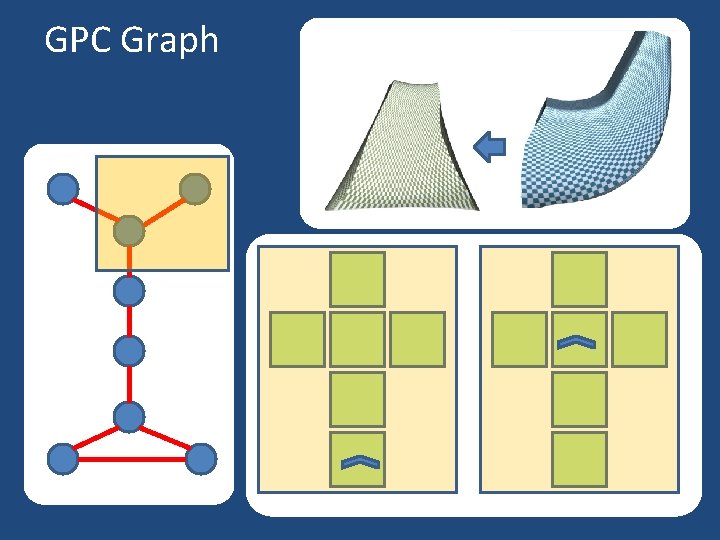
GPC Graph
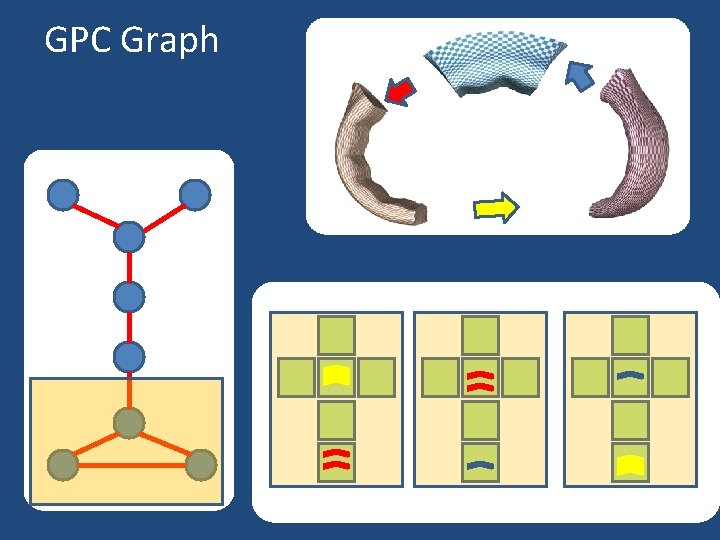
GPC Graph
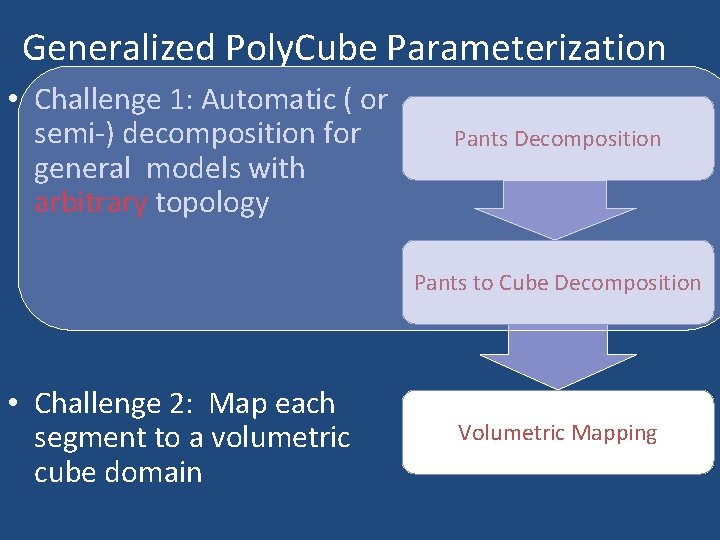
Generalized Poly. Cube Parameterization • Challenge 1: Automatic ( or semi-) decomposition for general models with arbitrary topology Pants Decomposition Pants to Cube Decomposition • Challenge 2: Map each segment to a volumetric cube domain Volumetric Mapping

Pants Decomposition • Challenge: Automatic decomposition for general models with arbitrary topology • Solution: Pants Decomposition – A homology basis of a closed genus-g surface can be computed automatically decomposed into a set of 2 g 2 pants patches [courtesy of Li et al. TVCG 2008]
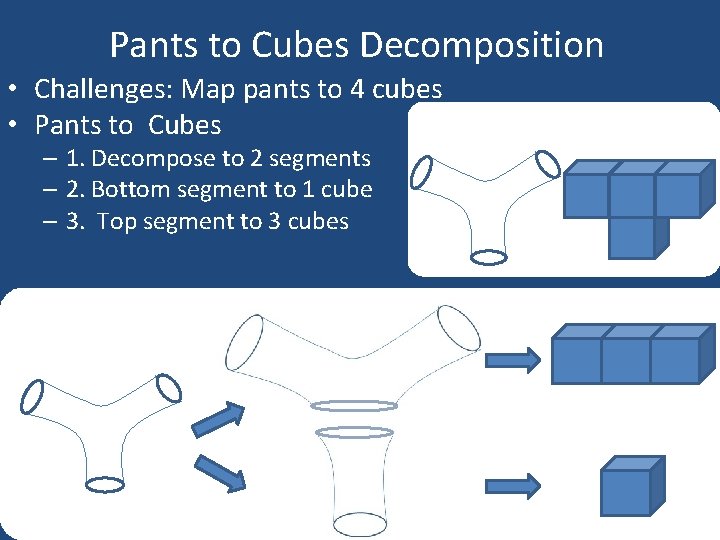
Pants to Cubes Decomposition • Challenges: Map pants to 4 cubes • Pants to Cubes – 1. Decompose to 2 segments – 2. Bottom segment to 1 cube – 3. Top segment to 3 cubes
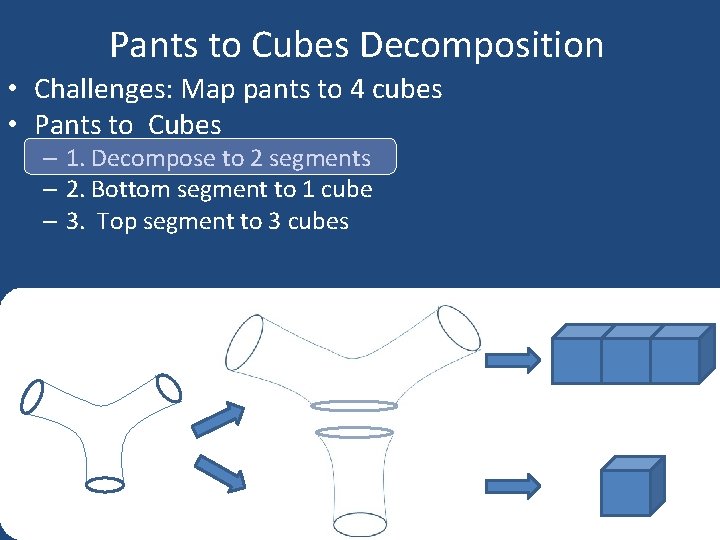
Pants to Cubes Decomposition • Challenges: Map pants to 4 cubes • Pants to Cubes – 1. Decompose to 2 segments – 2. Bottom segment to 1 cube – 3. Top segment to 3 cubes

Pants to Cubes Decomposition • Decompose to 2 segments automatically – 1. Solve Harmonic Function [Ni et al. Siggraph 2005] – 2. Detect saddle point – 3. Solve Harmonic Function ( new constriant) and cut pants
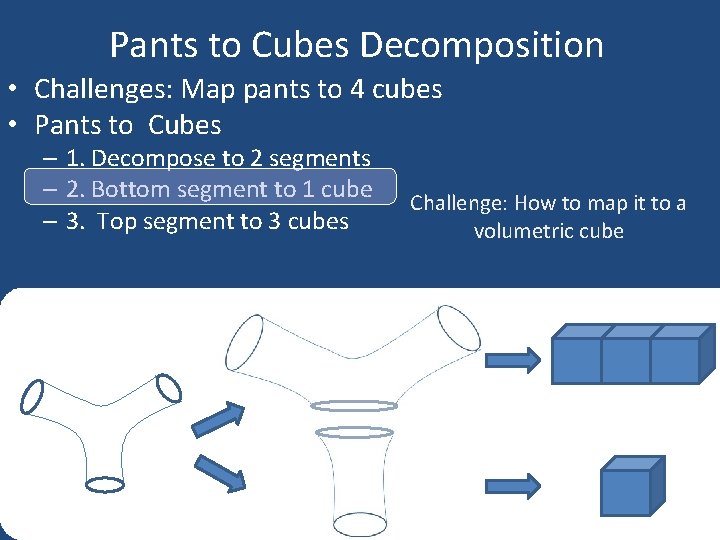
Pants to Cubes Decomposition • Challenges: Map pants to 4 cubes • Pants to Cubes – 1. Decompose to 2 segments – 2. Bottom segment to 1 cube – 3. Top segment to 3 cubes Challenge: How to map it to a volumetric cube
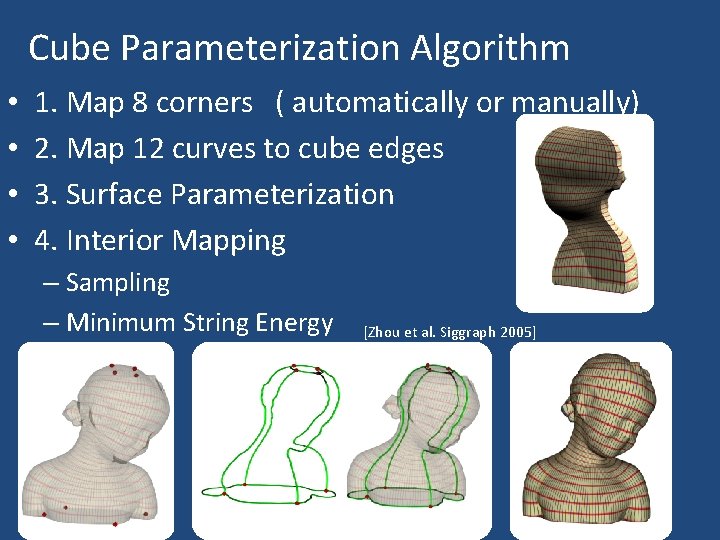
Cube Parameterization Algorithm • • 1. Map 8 corners ( automatically or manually) 2. Map 12 curves to cube edges 3. Surface Parameterization 4. Interior Mapping – Sampling – Minimum String Energy [Zhou et al. Siggraph 2005]
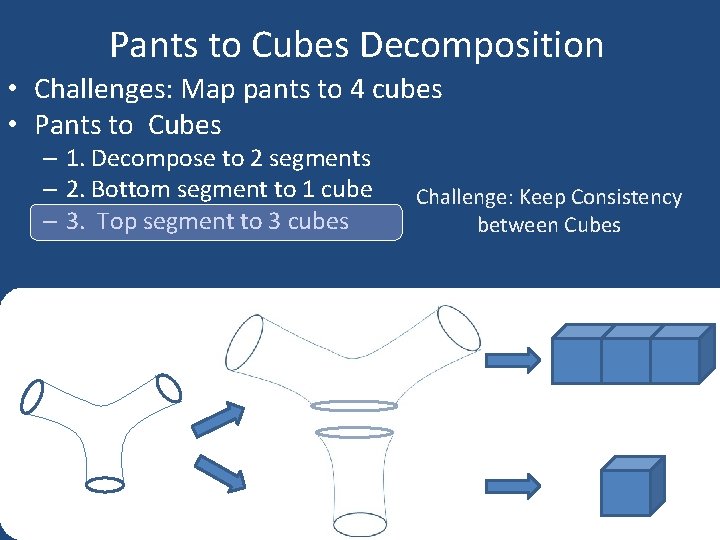
Pants to Cubes Decomposition • Challenges: Map pants to 4 cubes • Pants to Cubes – 1. Decompose to 2 segments – 2. Bottom segment to 1 cube – 3. Top segment to 3 cubes Challenge: Keep Consistency between Cubes
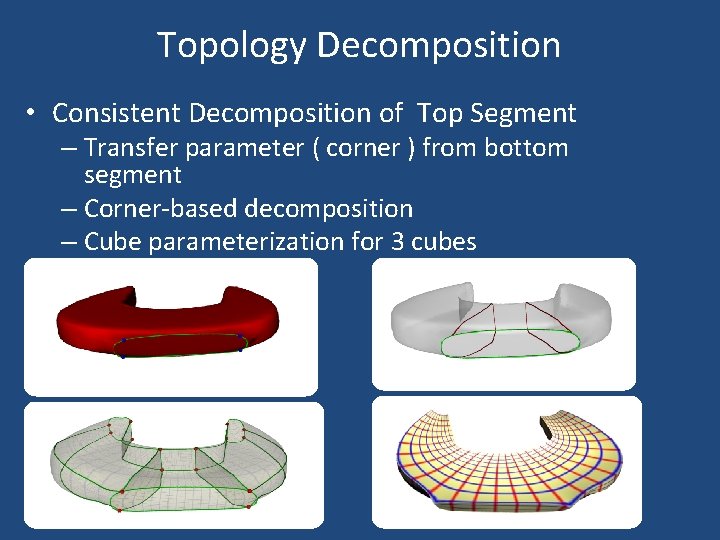
Topology Decomposition • Consistent Decomposition of Top Segment – Transfer parameter ( corner ) from bottom segment – Corner-based decomposition – Cube parameterization for 3 cubes

Goals • Global Volumetric Parameterization – Arbitrary Topology – Complex Geometry – Automatically ( Semi-Automatically) – Less Segments – Seamless – Low Distortion • Trivariate Spline – No Trimming – Global Continuity
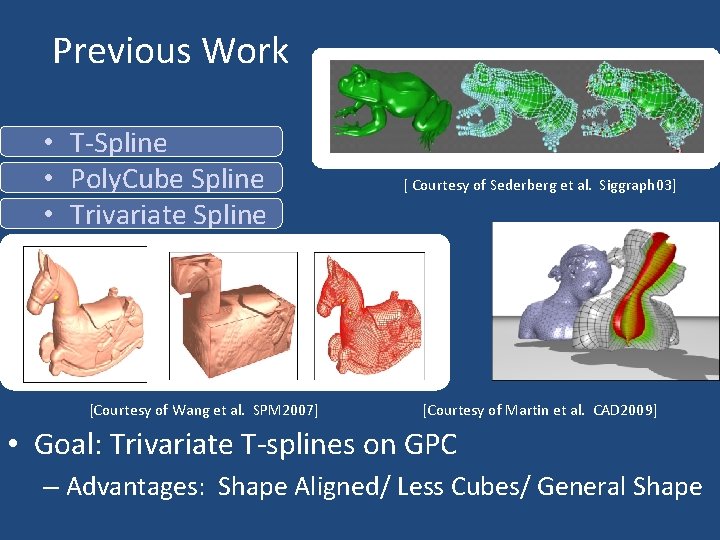
Previous Work • T-Spline • Poly. Cube Spline • Trivariate Spline [Courtesy of Wang et al. SPM 2007] [ Courtesy of Sederberg et al. Siggraph 03] [Courtesy of Martin et al. CAD 2009] • Goal: Trivariate T-splines on GPC – Advantages: Shape Aligned/ Less Cubes/ General Shape

Contributions • Efficient GPC Parameterization – Decompose model to cubes automatically – Glue Cubes to GPC consistently – Volumetric Cube Parameterization • Volumetric T-splines on GPC – Construct on GPC Domain (No Global Parameter) – Recursive Adaptive Fitting Algorithm – Octree -based High Efficient Knot Vector Computation

Trivariate T-Spline • For Each Control Point : – Knot Vectors – Basis Functions – Blending Function • Formulation

Trivariate T-Splines on GPC • Challenge: Global Representation of GPC – No embedded global parameterization, only local parameterization – Transition between adjacent cubes: translations/rotations • Update Formulation Superscript: Cube Domain Index Transfer local parameter from cube domain to Control point in cube with local parameter
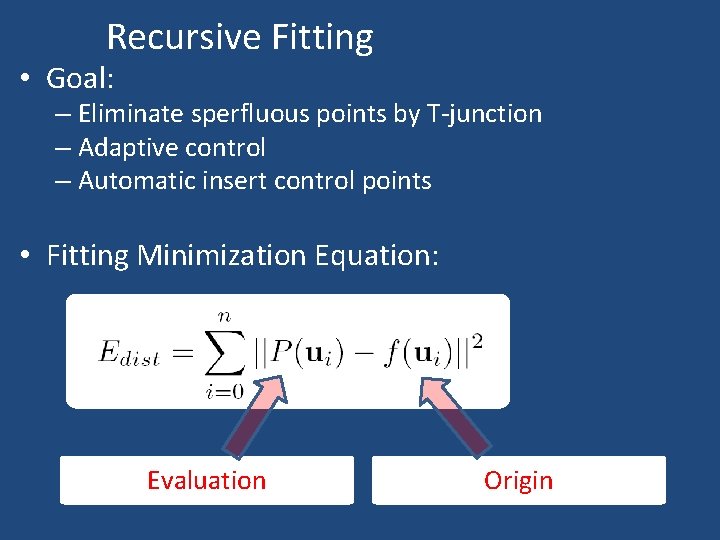
Recursive Fitting • Goal: – Eliminate sperfluous points by T-junction – Adaptive control – Automatic insert control points • Fitting Minimization Equation: Evaluation Origin

Fitting Algorithm
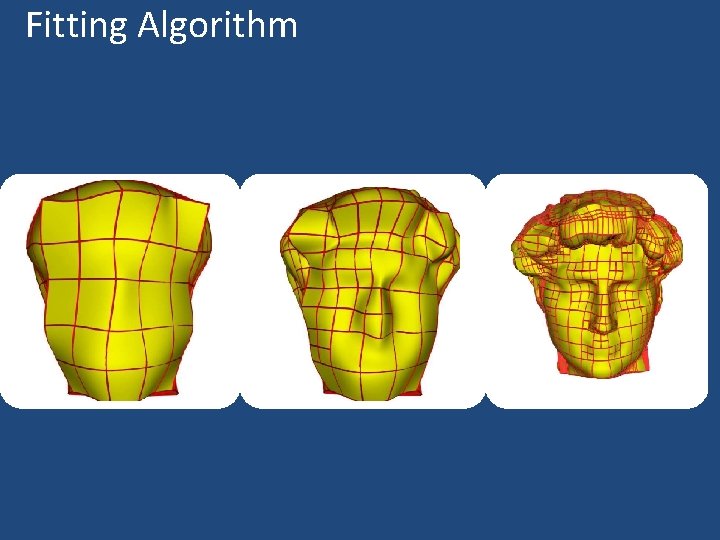
Fitting Algorithm

Implementation: Knot Vector

Knot Vector Computation • Getting knot vector: Ray tracing [ Sederberg et al. Siggraph 03] • Challenge: Ray tracing is difficult in 3 D case: – Detecting: Rays cross Point, Line, Face – No Global Parameter • Solutions: – Limited Cutting: A cube can only be divided into 8 cubes – The structure is converted to octree structure

Results


Conclusion • Global Volumetric Parameterization – Representation: Generalized Poly. Cube – GPC Construction: • Topology Decomposition • Cube Parameterization • Trivariate Spline – T-Spline Based on GPC – Fitting Algorithm and Implementation
- Slides: 40