Global Critical Path A Tool for SystemLevel Timing

Global Critical Path: A Tool for System-Level Timing Analysis Mihai Budiu May 23, 2007

Based On Critical Path: A Tool for System-Level Timing Analysis Girish Venkataramani, Tiberiu Chelcea, Mihai Budiu, and Seth C. Goldstein, Design Automation Conference (DAC), San Diego, CA, June 4 -8, 2007 Girish Venkataramani: summer intern here in 2005 Now graduating from CMU His Ph. D. thesis: A System Level Timing Analysis and Optimization Methodology for Hardware Compilation is based on the Global Critical Path 2

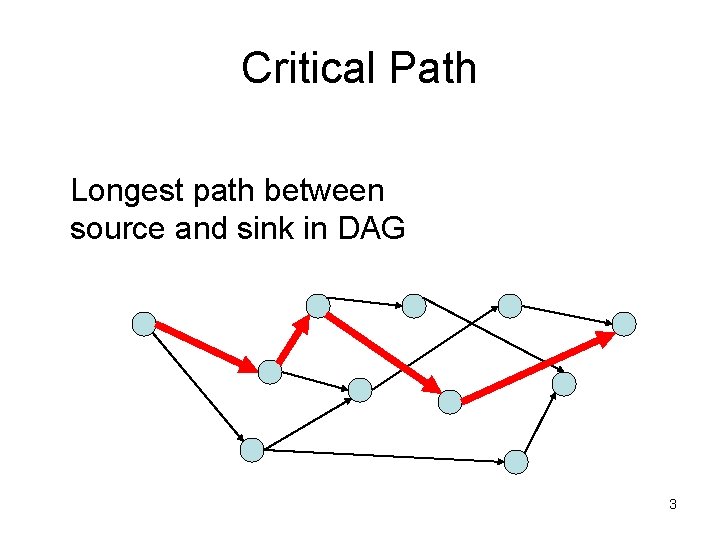
Critical Path Longest path between source and sink in DAG 3

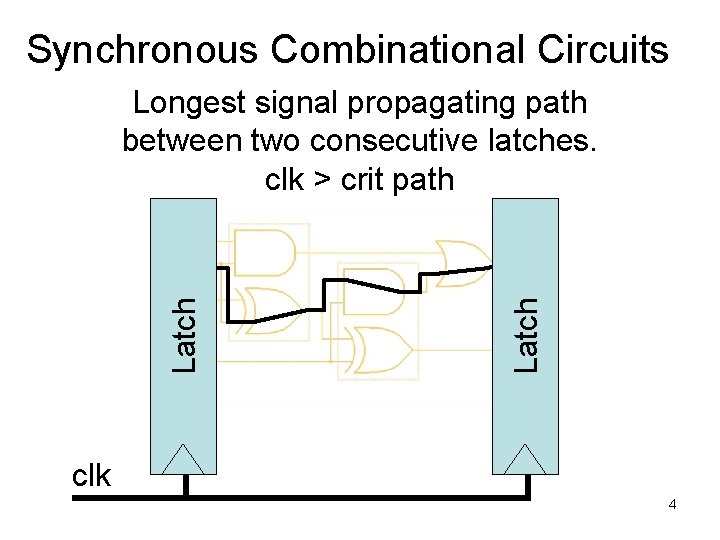
Synchronous Combinational Circuits Latch Longest signal propagating path between two consecutive latches. clk > crit path clk 4

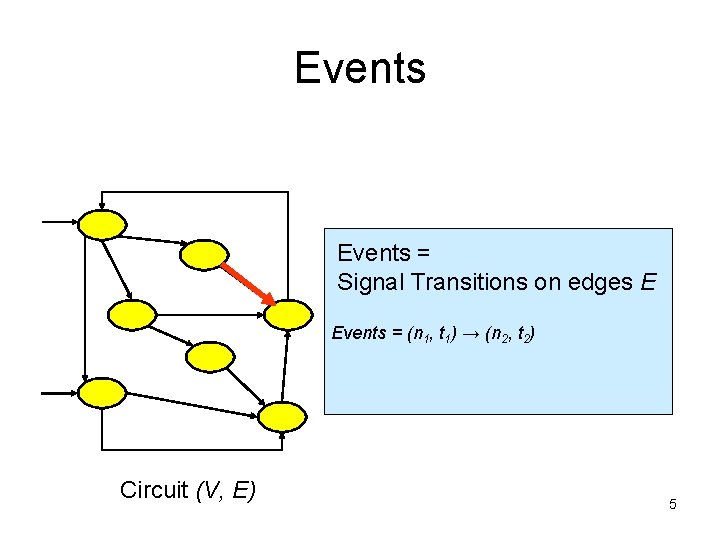
Events = Signal Transitions on edges E Events = (n 1, t 1) → (n 2, t 2) Circuit (V, E) 5

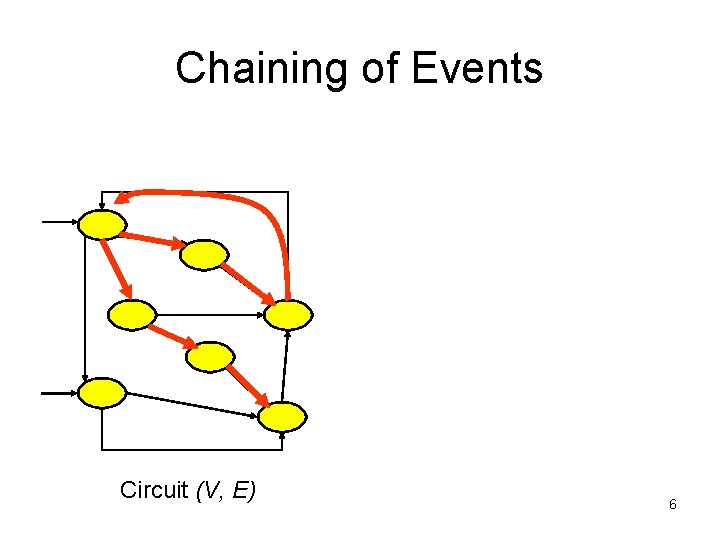
Chaining of Events Circuit (V, E) 6

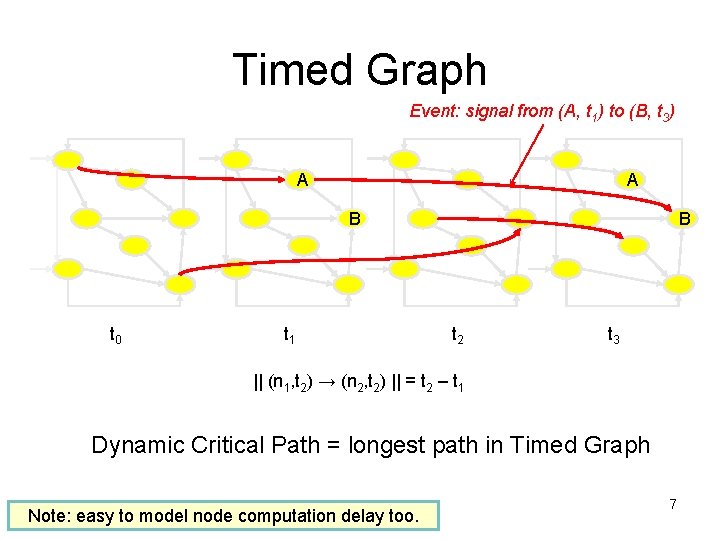
Timed Graph Event: signal from (A, t 1) to (B, t 3) A A B t 0 t 1 B t 2 t 3 || (n 1, t 2) → (n 2, t 2) || = t 2 – t 1 Dynamic Critical Path = longest path in Timed Graph Note: easy to model node computation delay too. 7

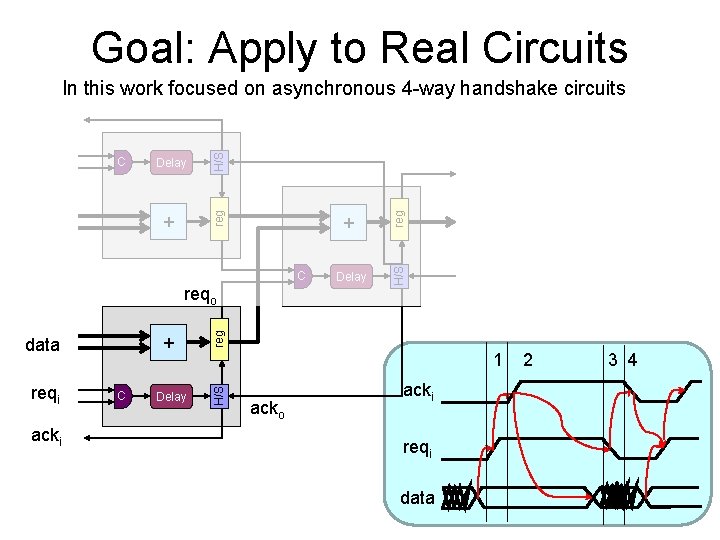
Goal: Apply to Real Circuits C reqi acki C Delay 1 H/S + data Delay reg reqo + reg + H/S Delay H/S C reg In this work focused on asynchronous 4 -way handshake circuits acko acki reqi data 2 3 4

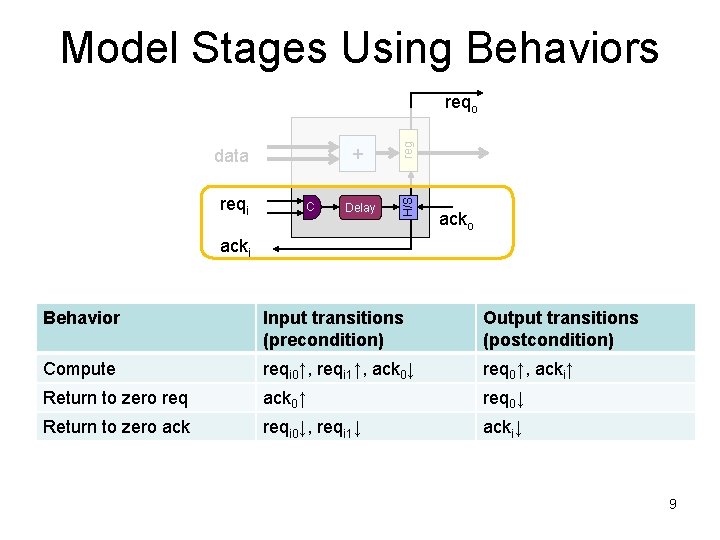
Model Stages Using Behaviors reqi C + reg data Delay H/S reqo acki Behavior Input transitions (precondition) Output transitions (postcondition) Compute reqi 0↑, reqi 1↑, ack 0↓ req 0↑, acki↑ Return to zero req ack 0↑ req 0↓ Return to zero ack reqi 0↓, reqi 1↓ acki↓ 9

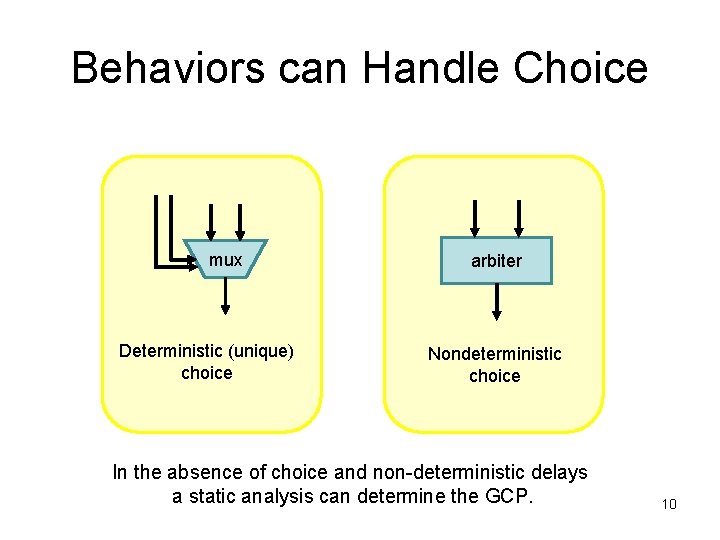
Behaviors can Handle Choice mux Deterministic (unique) choice arbiter Nondeterministic choice In the absence of choice and non-deterministic delays a static analysis can determine the GCP. 10

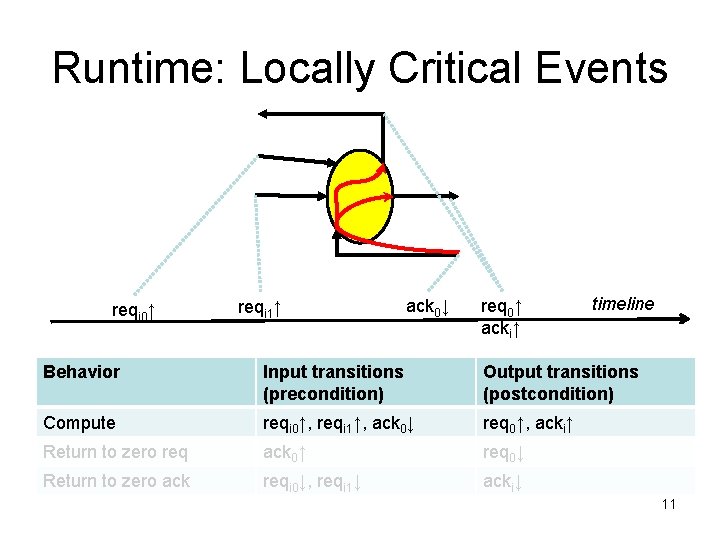
Runtime: Locally Critical Events reqi 0↑ reqi 1↑ ack 0↓ req 0↑ acki↑ timeline Behavior Input transitions (precondition) Output transitions (postcondition) Compute reqi 0↑, reqi 1↑, ack 0↓ req 0↑, acki↑ Return to zero req ack 0↑ req 0↓ Return to zero ack reqi 0↓, reqi 1↓ acki↓ 11

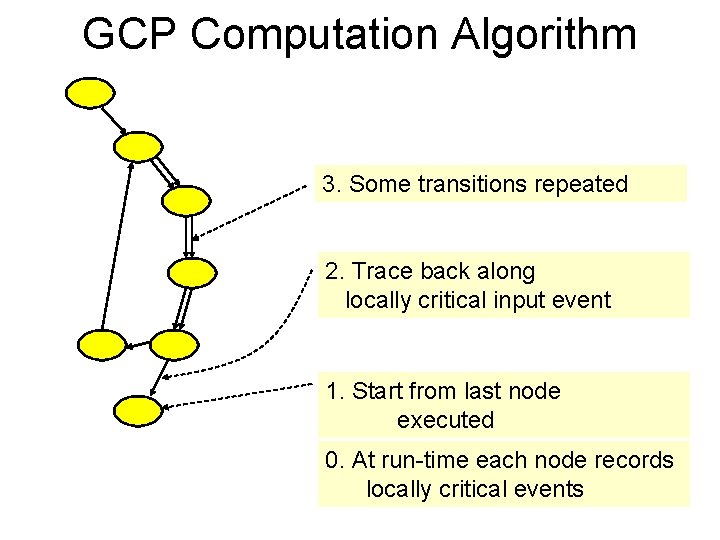
GCP Computation Algorithm 3. Some transitions repeated 2. Trace back along locally critical input event 1. Start from last node executed 0. At run-time each node records 12 locally critical events

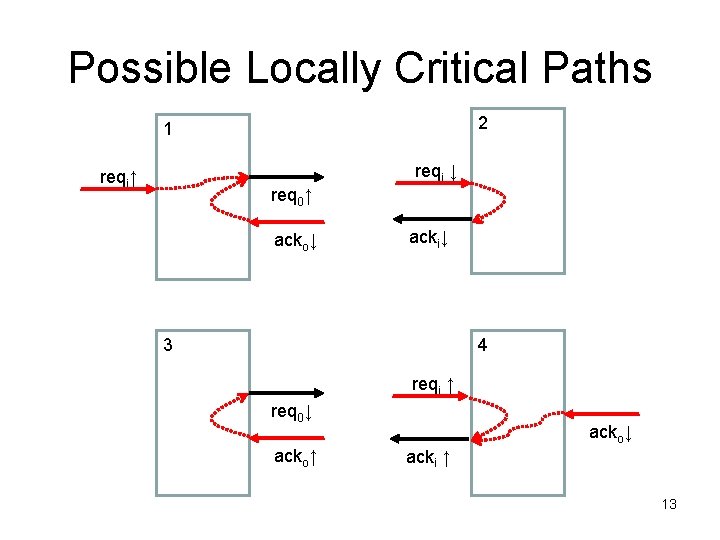
Possible Locally Critical Paths 2 1 reqi ↓ reqi↑ req 0↑ acko↓ acki↓ 3 4 reqi ↑ req 0↓ acko↑ acko↓ acki ↑ 13

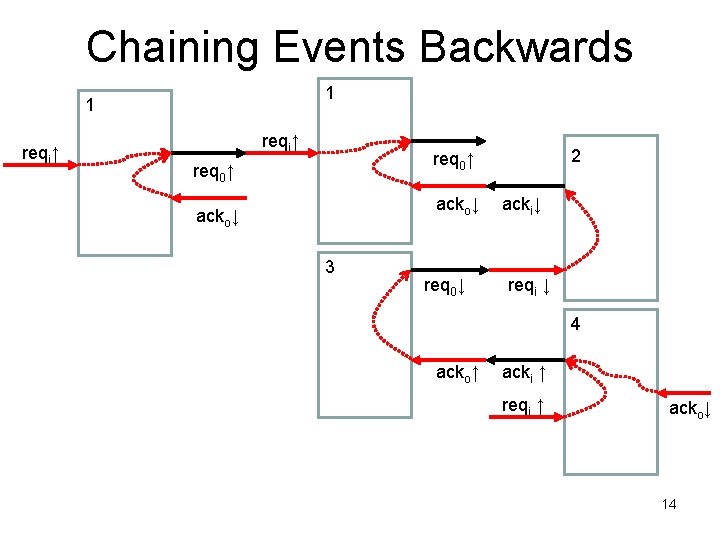
Chaining Events Backwards 1 1 reqi↑ 2 req 0↑ acko↓ 3 req 0↓ acki↓ reqi ↓ 4 acko↑ acki ↑ reqi ↑ acko↓ 14

Theorem PATHdata = [req↑]* PATHsync = [ack↑→ req↓→ ack↓]* GCP = [PATHdata → PATHsync]* 15

What does this mean? PATHdata = [req↑]* Good: wait for data PATHsync = [ack↑→ req↓→ ack↓]* Maybe bad: synchronization problem GCP = [PATHdata → PATHsync]* 16

An Example req. AD↑→ [req. DE↑→req. EG↑→ack. GC↑→req. CE↓→ack. ED↓]9 →req. DE↑→req. EG↑ →req. GM↑ →req. MN↑ req. AD↑→ [req. DE↑→req. EG↑→ack. GJ↑→req. JA↑]9 →req. DE↑→req. EG↑ →req. GM↑ →req. MN↑ 17

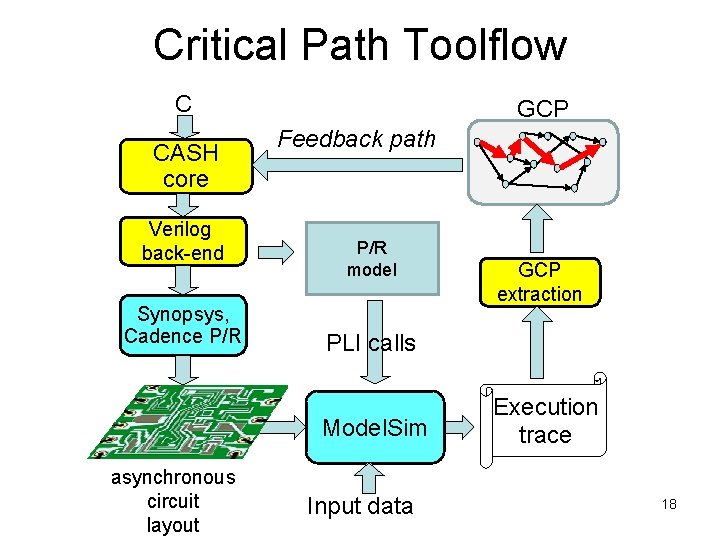
Critical Path Toolflow C CASH core Verilog back-end Synopsys, Cadence P/R GCP Feedback path P/R model PLI calls Model. Sim asynchronous circuit layout GCP extraction Input data Execution trace 18

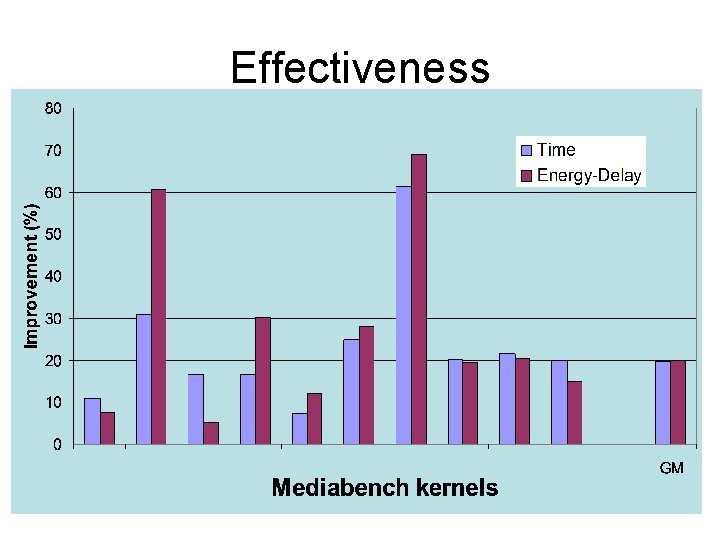
Effectiveness 19

Conclusions: Global Critical Path • • t 0 t 1 t 2 t 3 Is defined as a path on the timed graph. Tracks dependences. Can be computed by automatic tools. Summarizes concurrent computation bottlenecks. • Can be incorporated in a feedback loop. to drive optimizations and de-optimizations. 20 • Is a profiling (input-dependent) concept.