GLI ALGORITMI QR E QL Punto di partenza

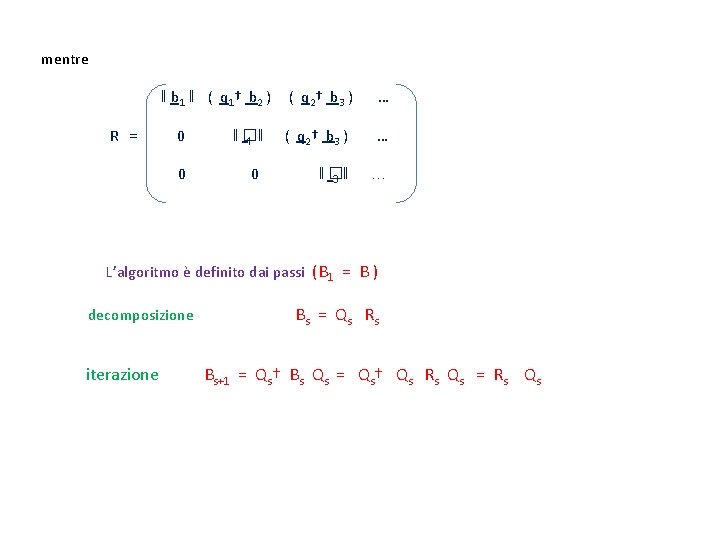
GLI ALGORITMI QR E QL Punto di partenza : ( Francis 1961 ) fattorizzazione QR ogni matrice non nulla B può essere decomposta come B = Q R con Q matrice unitaria ed R matrice triangolare superiore la decomposizione è unica se B è non singolare esiste ovviamente anche la decomposizione Q L con L triangolare inferiore La fattorizzazione QR è la formulazione matriciale della procedura Gram-Schmidt per ortogonalizzare le colonne della matrice B nell’ordine b 1 , b 2 , . . . , bn Le colonne di Q sono definite da q 1 = b 1 / ‖ b 1 ‖ � i = bi - k qk ( qk† bi ) k = 1, …, i-1 qi = � i /‖� i‖

mentre ‖ b 1 ‖ ( q 1 † b 2 ) R = ( q 2 † b 3 ) … 0 ‖� 1‖ ( q 2 † b 3 ) … 0 0 ‖� 3‖ … L’algoritmo è definito dai passi (B 1 = B ) decomposizione iterazione Bs = Qs Rs Bs+1 = Qs† Bs Qs = Qs† Qs Rs Qs = Rs Qs

e dal Teorema Siano 0 < 1 2 n gli autovalori di B e z 1 , z 2 , … , zn i corrispondenti autovettori normalizzati. Allora, se zi † ei 0 Bs ei i ei s ∞ algoritmo di elezione per il calcolo di tutti gli autovalori ed autovettori di una matrice generale ( non necessariamente simmetrica o hermitiana ) Caratteristiche stabilità numerica Preserva caratteristiche di simmetria delle matrici. In particolare matrici hermitiane : trasforma matrici tridiagonali in matrici tridiagonali matrici generali : conserva la forma di Hessenberg

Algoritmi estremali Vettori e spazi di Krilov Dato un vettore non nullo f ed una matrice A matrice di Krilov К(m) ( f , A ) ={f , A 2 f , …… , Am-1 f } sottospazio di Krilov K (m) ( f , A ) = span ( К(m) ( f , A ) ) è lo spazio vettoriale generato dalle combinazioni lineari delle colonne di К(m) ( f , A ) - questioni connesse alla possibile ortogonalità di f all’autospazio di A. In pratica, gli errori di arrotondamento rendono del tutto futile la questione. Osservazione 1 - se A è m x m allora dim ( K (m) ( f , A )) = m le colonne della matrice di Krilov sono una base per lo spazio generato da f ed A, i. e. Am f è loro combinazione lineare.

Algoritmo di Lanczos Punto di partenza: applichiamo alla matrice di Krilov la decomposizione QR Osservazione 2 - La procedura sembra richiedere costruzione delle colonne di К(m) ( f , A ) ortogonalizzazione è possibile costruire direttamente le colonne di Q ESEMPIO Poiché q 3 Є K (3) ( q 1 , A ) allora span( q 1 , q 2 , q 3 , A q 3 ) = span( q 1 , q 2 , q 3 , A(r 2 A 2 + r 1 A + r 0 ) q 1 ) = = span( q 1 , q 2 , q 3 , A 3 q 1 ) = K (4) ( q 1 , A ) → trovati q 1 , q 2 , q 3 il quarto vettore si trova ortogonalizzando A q 3 rispetto a q 1 , q 2 e q 3

Osservazione 3 - ∀ j < m A K (j) ϵ K ma qi ortogonale K quindi qi † ( A qj ) = 0 (j+1) (i-1) A qi ϵ K (j+1) ∀ i > j+1 e per la simmetria di A qi † ( A qj ) = qj † (A qi ) = 0 ∀ j < i-1 la matrice Q† A Q è tridiagonale − il passo costoso della procedura è il calcolo di A qi n 2 operazioni − evidentemente la procedura è conclusa con la costruzione del vettore qm-1. Tuttavia è possibile mostrare che