Glasgow Counts A Framework for Mathematics Early Level

Glasgow Counts A Framework for Mathematics Early Level

Tracker 1 Home Learning 2 Recalls the Number sequence forwards and backwards, from zero to at least 10, from any given number. Orders numbers forwards & backwards to at least 10. Identifies the number before, after and missing numbers in a sequence. Recalls the Number sequence forwards and backwards, from zero to at least 30, from any given number. Orders numbers forwards & backwards to at least 20. Identifies the number before, after and missing numbers in a sequence. Recognises number names and numerals to at least 10. Explains that zero is represented by the numeral ‘ 0’. Recognises number names and numerals to at least 20. Orders numbers forwards & backwards to at least 20. Identifies the number before, after and missing numbers in a sequence. Identifies ‘how many? ’ in regular & irregular dot patterns, five frames and dice without having to count – SUBITISING. Identifies ‘how many? ’ in regular & irregular dot patterns, arrays, five frames, ten frames and dice without having to count – SUBITISING. Counting No. word sequences Checks a solution by comparing with the estimate. (embedded through all strands) Numerals Tracker 2 Subitising Numeracy Progression Pathways: Early Level Understands and uses the language of estimation. (embedded through all strands) Understands cardinal numbers - sorting, classifying, acquiring number & conservation of number. Compares quantities using appropriate language. Place Value Awareness of Number – Counting, Quantities & Number Structure Estimation and Rounding Home Learning 1 Addition and Subtraction (Part, Whole Relationshi ps) Multiplicati on and division Fractions, decimals Uses 1 -to-1 correspondence to count objects to at least 10. When counting, understands that the last number counted is the total. Uses 1 -to-1 correspondence to count a given number of objects to at least 20. Uses ordinal numbers in real life contexts. Counts in jumps (skip counts) in 2 s, 5 s and 10 s and begins to use this as a useful strategy to find how many in a larger group. Partitions single digit numbers into two parts. Explains that zero means there is none of a particular quantity. Partitions single digit numbers into two or more parts and recognises that this does not affect the total. Demonstrates understanding of all possible partitions of numbers to at least 10. Using concrete resources , solves problems that involve addition and subtraction. Shares out a group of items equally into smaller groups. Doubles numbers to a total of at least 10. Splits a whole into at least halves and uses appropriate language. Counts on and back in ones to demonstrate understanding of addition and subtraction. Use appropriately the mathematical symbols +, -, =. Translate a word problem into a number sentence. Shares out a group of items equally into smaller groups. Finds the total of equal groups. Links number families when explaining mental strategies for addition & subtraction. Solves simple missing number equations, for example, 3 + ● = 10. Uses a range of strategies to add and subtract mentally to at least 10. Doubles numbers to a total of at least 20. Splits a whole into smaller and explains that ‘equal parts’ are the same size. Uses appropriate vocabulary to describe each part, to at least halves and quarters.

Recalls the Number sequence forwards and backwards, from zero to at least 10, from any given number. Orders numbers forwards & backwards to at least 10. Identifies the number before, after and missing numbers in a sequence. Language number, count (forwards, up, on, to, backwards, down, back, to), zero, one, two, three, …, ten, order, alternate, every other, take turns, odd, even, next, after, before. Example Activities are generally oral and the following terminology and procedure can be followed: • I’m going to count from 0 to 3 and I want you to say it after me. Ready; zero, one, two, three. • Extend in the range 4 to 6, 7 to 10, 0 to 5, 6 to 10 and 0 to 10. • I’m going to count back from 3 and I want you to say it after me. Ready; three, two, one, zero. • Extend the range to 7 to 4, 10 to 8, 5 to 0, 10 to 6 and 10 to 0. • Take turns to say the numbers. I will say zero then you say one, then I will say two and you say three and we will continue up to ten. Ready: zero (one) two (three) four……. etc. • Extend in the range 0 to 10 and repeat using backwards sequences. • I’m going to count and I want you to say the next number after I stop. Ready: zero, one, two, … Extend in the range 0 to 10 and repeat using backwards sequences. • I'm going to say a number and I want you to say the number that comes just AFTER. Ready: four! (FIVE) six! (SEVEN) etc • I’m going to say a number and I want you to say the number that comes BEFORE. Ready: four! (THREE) six! (FIVE) etc. Potential Barriers / Misconceptions • Learners may find it difficult to say FNWSs that do not start from 1 so lots of opportunities should be given. They may have little understanding of the value of each number so while able to count to 10, they may not be able to count with 1 to 1 correspondence. • BNWSs are usually significantly more difficult than FNWSs. Learners at this level will use a dropping back strategy in order to determine the required number word i. e. the child may say ‘one, two, three, four, five’ to determine what comes before 5. Allow Learners sufficient thinking time and an opportunity to reflect. • Reflection on spoken number words in various ways can strengthen the child’s knowledge of FNWS and BNWS. If the child has continuing difficulty with saying BNWS’s, have the child repeat short sequences after the teacher. • Learners will encounter greater difficulty the less numbers provided when saying the next number word forwards or back. Choose the difficulty of the tasks carefully so as to avoid Learners guessing without thinking very much. Resources Counting Stick Cf. E MNU 0 -02 a Learning Intentions • • Say short forward number word sequences. Say short backward number word sequences. Say alternate numbers. Say next number word forward. Say next number word backward. Say number word after. Say number word before. Key Questions • Can you count on from 3 to 8 (6 to 12, 8 to 15, etc. )? • Can you count back from 7 to 2 (8 to 4, 10 to 0, etc. )? • Can you take turns counting from 0 forwards to 8, 10 backwards to 3, etc. ? • What number comes next? Five, six, seven, … • I’m going to count down from seven. Can you tell me which number comes next? Seven, six, five, … • What number comes after 3? • What number comes before 7? Assessment Benchmark Recalls the Number sequence forwards and backwards to at least 30 from any given number. Orders numbers forwards & backwards to at least 20. Identifies the number before, after and missing numbers in a sequence.

Recalls the Number sequence forwards and backwards, from zero to at least 30, from any given number. Orders numbers forwards & backwards to at least 20. Identifies the number before, after and missing numbers in a sequence. Language number, count (forwards, up, on, to, backwards, down, back, to), zero, one, two, three, …, thirty, order, alternate, every other, take turns, odd, even, next, after, before. Example Activities are generally oral and the following terminology and procedure can be followed: • Start from 18 and count up to 24. (Start counting on from 12 and I'll tell you when to stop) • Start from 12 and count back to 8. (Start counting back from 21 and I'll tell you when to stop) • Take turns to say the numbers. I will say zero then you say one, then I will say two and you say three and we will continue up to twenty. Ready: zero (one) two (three) four……. etc. • Repeat using backwards sequences. • I’m going to count and I want you to say the next number after I stop. Ready: ten, eleven, twelve, … Ready: eighteen, nineteen, twenty, . . . • Repeat using backwards sequences. • I'm going to say a number and I want you to say the number that comes just AFTER. Ready: four! (FIVE) six! (SEVEN) etc. • I’m going to say a number and I want you to say the number that comes BEFORE. Ready: four! (THREE) six! (FIVE) etc. • These activities should be developed progressively in the range 0 to 20 then extended to numbers to at least 30. • A counting stick can be used to support learner's understanding for the activities above. Potential Barriers / Misconceptions • BNWSs in the teens are usually much more difficult for Learners than FNWSs. • Learners often use a dropping back strategy to determine a particular number word, for example, the child says the FNWS from ten to figure out what comes before 'fourteen'. As the child's knowledge of number word sequences improves they should rely less and less on this strategy. • Some Learners may have difficulty with a specific number word and consistently omit it. • The ability to say one, two or three number words backwards, forms an important foundation for counting down strategies. Learners are likely to find it more difficult when fewer number words are said by the teacher. Resources Counting Stick Cf. E MNU 0 -02 a Learning Intentions • • Say short forward number word sequences. Say short backward number word sequences. Say alternate numbers. Say next number word forward. Say next number word backward. Say number word after. Say number word before. Key Questions • Can you count on from 13 to 22 (6 to 25, 19 to 30, etc)? • Can you count back from 7 to 2 (13 to 8, 17 to 9, etc)? • Can you take turns counting from 12 forwards to 30, 29 backwards to 11, etc. ? • Can you help me count from 1 to 16? I’m going to count the odd numbers and I want you to count the even. • Can you count the next three numbers? Ready: twentythree, twenty-four, … • Can you count the next three numbers backwards? Ready: twenty-three, twenty-two, … • What number comes after 23? • What number comes before 25? Assessment Benchmark Recalls the Number sequence forwards and backwards to at least 30 from any given number. Orders numbers forwards & backwards to at least 20. Identifies the number before, after and missing numbers in a sequence.

Recognises number names and numerals to at least 10. Explains that zero is represented by the numeral ‘ 0’. Language two, number, numeral, count (forwards/backwards, up/down, on/back, to/from), zero, one, three, …ten, order, increasing, decreasing, random. Example Activities • Place out the cards from 0 to 3, randomly arranged. Point to the number 2. Point to the number 3. etc • Place out the cards from 0 to 3, randomly arranged. Point to the card for 2. What number is this? • Place the cards from 0 to 3 in a pile, face down and randomly arranged. I am going to turn over each card in turn. Tell me the number on the card. What number is this? • Place out the numeral sequences from 0 to 3. Watch me as I count from 0 to 3. Now you count from 0 to 3 and point to each one. • Place out the numeral sequences from 0 to 3. Watch me as I count forwards and backwards. 0, 1, 2, 3; 3, 2, 1, 0. Now you say the numbers and point to each one like I did. • Place out the numerals from 0 to 3 randomly. Put these cards in order from zero. Say the numbers as you point to them. • Place out the numeral track from 1 to 5, with numerals uncovered. Watch me as I count forwards and backwards. Now you count forwards & backwards & point to each number in turn. • Close lids on the numeral track and repeat previous activity. Uncover the lids AFTER saying each number. • Place out the numeral track from 1 to 5, with numerals covered. Uncover numeral 3. What number is this? Leave numeral 3 uncovered and point to the lid covering the numeral 4. What number is that? • Direct the child to uncover numeral 4. Check if you were you correct? • Repeat each activity above for cards from 0 to 5, 6 to 10 and 0 to 10. Potential Barriers / Misconceptions • Some Learners can recognise the numerals from 0 to 5, but will have difficulty recognising 6 to 10. Some Learners may confuse specific numerals. In such cases a discrimination task will beneficial whereby the child is presented with a pile of number cards (containing either 6 or 8). The task being to sort the cards into 2 piles. • A child’s emerging knowledge of forward and backward number sequences supports learning of numerals and vice-versa. Learners might initially have difficulty in coordinating each point with saying the corresponding number word. In such cases the teacher should model the activity slowly for the child. • Learners might have difficulty after saying the last number word forward and then attempting to say the first number word backwards. They might say ‘ 0, 1, 2, 3, 4, 3, 2, 1, 0’ or ‘ 0, 1, 2, 3, 4, 5, 6’. Careful modelling by the teacher will be required. • Learners are likely to encounter more difficulty when there are more cards, for example , ordering 0 -3. The teacher should determine the range of numeral cards which is just beyond the range which the child can order without difficulty. Resources Cf. E MNU 0 -02 a Learning Intentions • • • Recognise numerals to at least 10. Identify (name) numerals to at least 10. Sequence numerals forwards and backwards. Key Questions • Can you point to the number 6 on the line? • Can you find the number 4 anywhere in the room? • Can you press the number 7 on this phone? • What number is beside the peg? • Can you read me the number on this card? • What number is above the 5 on this phone? • Can you point to and count on from 0 to 5 (3 to 8, 5 to 10, etc. )? • Can you point to and count back from 5 to 0 (8 to 3, 10 to 5, etc. )? • Can you point to / place these numbers in the correct order? Assessment Benchmark Recognise number names and numerals to at least 20. Orders numbers forwards and backwards to at least 20. Identifies the number before, the number after and missing numbers in a sequence. Explains that zero means there is none of a particular quantity and is represented by the numeral ‘ 0’.

Recognises number names and numerals to at least 20. Orders numbers forwards & backwards to at least 20. Identifies the number before, after and missing numbers in a sequence. Language two, number, numeral, count (forwards/backwards, up/down, on/back, to/from), zero, one, three, …twenty, order, increasing, decreasing, random. Example Activities • Place out the cards from 11 to 15 randomly arranged. Point to the no. 12. Point to the no. 14. • Place out the cards from 11 to 15, randomly arranged. Point to the card for 16. What number is this? Place out the numeral sequence from 11 to 15. Watch me and listen as I count forwards and backwards. Point to each numeral in turn, while counting from 11 to 15, and then from 15 to 11. Eleven, twelve, … fifteen. Fifteen, fourteen, … eleven. • Place out the cards from 11 to 15, randomly arranged. Put these cards in order. Now say the numbers as you point to them. • Place out the numeral track from 11 to 15 (numerals uncovered). Point to each numeral in turn, while counting from 11 to 15, and then 15 to 11. Now you can count forwards and backwards and point to each number in turn. • Close lids and repeat previous activity, uncovering the lids after saying each number. • Place out the numeral track from 11 to 15 (numerals covered). Uncover 13. What number is that? Leave 13 uncovered and point to the lid covering 14. What number is that? Direct the child to uncover 14. Were you correct? • Similarly with the numeral sequence from 16 to 20 and 11 to 20 and 1 to 20. Potential Barriers / Misconceptions • Learner's knowledge of the corresponding FNWS facilitates the activity of reading a numeral sequence forwards. Thus a child might appear to be reading the numerals from 11 to 15 in turn when their response is based mainly on their knowledge of the sequence of number words from eleven to fifteen. • Some Learners might be able to arrange a set of numerals in the correct sequence (e. g. the numerals from 11 to 15) without necessarily being able to name all of the numerals. Some Learners find recognition easier than identification of numerals. E. g. Some Learners may recognise 12 but have difficulty in identifying the appropriate number word 'twelve'. • Some Learners identify 13 to 19 by reading one digit at a time starting with the right hand digit. As a result, Learners may have difficulty with identifying '12' reading it as '21' instead. Learners can and should learn the name of 2 -digit numerals at a time when they might have little understanding of the place value associated with the numerals. Learners may frequently confuse particular numerals. In such cases, visual discrimination tasks can be useful. E. g. use a pile of cards where either ‘ 12’ or ‘ 21’ appears on each card, the child’s task being to sort the cards into 2 piles. Resources Cf. E MNU 0 -02 a Learning Intentions • • • Recognise numerals to at least 20. Identify (name) numerals to at least 20. Sequence numerals forwards and backwards. Key Questions • Can you point to and count on from 12 to 17? • Can you point to and count back from 12 to 7? • Can you point to / place these numbers in the correct order? • Can you point to the number 12 on the line? • Can you find the number 19 anywhere in the room? • Can you key in the number 16 on the keyboard? • What number is beside the peg? • Can you read me the number on this card? • What number is above the 5 on this phone? Assessment Benchmark Recognise number names and numerals to at least 20. Orders numbers forwards and backwards to at least 20. Identifies the number before, the number after and missing numbers in a sequence. Explains that zero means there is none of a particular quantity and is represented by the numeral ‘ 0’.

Identifies ‘how many? ’ in regular & irregular dot patterns, five frames and dice without having to count - subitising. Language How many, dots, patterns, objects, flash, dice, domino, fiveframe, array. Cf. E MNU 0 -01 a MNU 0 -02 a Example Activities Learning Intentions • Provide opportunities for Learners to: • Count objects in a group (regular & irregular arrangements) • Identify numbers in a group without counting – Subitise (Numbers to at least 5) • Count objects in a group progressing to identifying numbers without having to count. • Display domino card for 1. How many dots do you see? Repeat for 2, 3 and 4 in order then randomly. • Flash cards 1 to 4 in order then randomly. • Repeat above sequence using random array cards 1 to 4. • Repeat for domino cards 1 to 6. • Repeat above for 5 frames. • Visualise patterns of objects • Display domino card for 2. Make a pattern in the air to show the number of dots. Can you do it without looking at the card? Tell me how many dots you see. Repeat for domino cards 1 to 4. • Flash domino card for 3. Look at the pattern and make a pattern in the air to show the number of dots. Repeat for domino cards 1 to 4. • Repeat above sequence using random array cards 1 to 4. • Repeat for domino cards 1 to 6. • Repeat above for 5 frames. • Display Domino card for 4. Clap your hands to show the number of dots on the card. • Flash domino card for 3. • Repeat for same progression as above. Potential Barriers / Misconceptions • Learners may make coordination errors if they require to count each dot / item individually from 1. An important goal is for Learners to develop strong conceptually based spatial patterns. i. e. they are able to visualise a pattern for each number. This skill will support Learners’s ability to combine and partition small numbers. • It is important that multiple representations of each number are displayed when using random array card in order that learners understand that the appearance of the group has no impact on the total number of objects. Conceptually based spatiomotor patterns can form a basis for Learners emerging strategies for adding and subtracting. Resources Key Questions • How many spots? Can you tell me without having to count them all? • Can you tell me how many spots when I flash and hide the pattern? • How many fish can you see? Can you tell me without having to count them all? • How many circles did you see in the picture? Can you tell me without counting? • Can you make the pattern in the air? • How many dots / objects can (did) you see? Clap your hands to show the number. Assessment Benchmark Identifies ‘how many? ’ in regular & irregular dot patterns, arrays, five frames, ten frames and dice without having to count (subitising).

Identifies ‘how many? ’ in regular & irregular dot patterns, arrays, five frames, ten frames and dice without having to count (subitising). Language How many, dots, patterns, objects, flash, dice, domino, tenframe, array. Example Activities • Provide opportunities for Learners to: • Represent a number using fingers simultaneously (throw): • Watch me use my fingers to make a number by raising all my fingers at once (model). Now you try. • Demonstrate ‘throwing’ a number unseen (bunny ears) and challenge Learners to do the same. • Repeat for numbers 0 to 5 randomly (using both hands). • Make 5 on one hand like I am doing. Now make on the other hand. How many fingers raised altogether? Repeat for 5 and 2, . . . 5 and 5 (seen progressing to unseen). • Identify numbers in a group without counting: • Place out an empty ten frame. Place 5 red counters in the upper row and 2 green counters in the lower row. How many counters altogether? How many red counters? How many green counters? • Repeat for other combinations with 5 (5 & 1, 5 & 3, 5 & 4, 5 & 5). • Repeat above but flashing printed ten frames rather than placing out the counters on blank frames. • Use random arrays cards / arrangements of objects to develop subitising and the ability to visually partition numbers (extending the range developed previously to at least 10): • How many dots can you see? • What smaller groups can you see? Cf. E MNU 0 -01 a MNU 0 -02 a Learning Intentions • Represent a number using fingers (throw) • Count objects in a group (regular & irregular arrangements) • Identify numbers in a group without counting – Subitise (to at least 10) Key Questions • Can you throw me 4 using your fingers? Can you use your other hand? Bunny ears? I can see a 4 and a 4 I can see 8 Potential Barriers / Misconceptions Initially Learners can look at the teacher’s pattern but cannot see their own pattern. Following this Learners can be directed without the teacher providing a model. For numbers beyond 2, Learners may raise 2 fingers simultaneously then the remaining fingers sequentially. An important goal of the activities is for Learners to develop more sophisticated ways of reasoning about their finger patterns. Teaching should focus on creating situations in which Learners can explicitly reflect on their mathematical activity. Teacher modelling, practice and reflecting on one's activity should be used to advance Learners from sequentially raising fingers to simultaneously raising fingers. Some Learners might count their fingers from one and others count on from five. I can see a 3, 3 and a 2 Resources • Can you throw me 8 using finger patterns? How many on each hand? Can you throw me 8 using bunny ears? • How many circles did you see in the picture? Can you tell me without counting? What other groups of circles did you see? Assessment Benchmark Identifies ‘how many? ’ in regular & irregular dot patterns, arrays, five frames, ten frames and dice without having to count (subitising).

Understands cardinal numbers - sorting, classifying, acquiring number & conservation of number. Language Sort, group, classify, more, less, same, justify. Cf. E MNU 0 -01 a MNU 0 -02 a Example Activities Learning Intentions • Sorting - Provide opportunities for Learners to sort objects into 2 sets – (extend by increasing no. of sets): i. Learners decide on criteria for sorting. iv. Sort by preference e. g. likes & dislikes. ii. Sort by colour e. g. red or green. v. Sort by types of objects e. g. books & pencils. iii. Sort by properties e. g. tall or short, shape, etc. • Classifying • Learners justify choices for sorting into a particular group – “This belongs to this group because…” • Acquiring Number • Set up a display area with various collections of 3 e. g. 3 pencils, 3 buttons, etc. • Ask, “What is the same about each plate? ” • Learners to make a collection of 3 objects from around the room e. g. 3 pens, 3 cups, etc. • Conservation of Number • Spread out two rows of coins, one set close together, the other set further apart. Ask, “Which row has more coins? ” • Use dot patterns in various arrangements to represent the same number. Challenge Learners to match patterns e. g. • Sort objects into sets. • Classify objects in a set. • Understand that number identifies ‘how many’ in a set. • Understand that the number of objects is not affected by position. = = NB. As objects are used to represent numbers, Learners need to be able to distinguish between properties that are relevant and irrelevant in counting. E. g. Colour is irrelevant when counting counters. Length is irrelevant when counting pencils. Potential Barriers / Misconceptions Resources Learners may be unable to articulate their reasons for sorting objects into particular sets. Learners may be unable to distinguish between relevant and irrelevant properties when counting. Learners may incorrectly associate quantity with irrelevant properties e. g. size or position. For example, they may determine that… is more than OR is more than Key Questions • Can you sort the toys into 2 groups? • Why have you put these toys together? • Put out different groups with same number of items…What is the same about each of these groups? • Line Learners up in 2 equal rows, one close together, one further apart. Which line has more Learners? • Can you match these patterns? (use patterns of items set out in different arrangements) Assessment Benchmark When counting objects, understands that the number name of the last object counted is the name given to the total number of objects in the group. Groups items recognising that the appearance of the group has no effect on the overall total (conservation of number).

Compares quantities using appropriate language. Language Group, collection, justify, compare, lots, few, less, more, same as. MNU 0 -01 a MNU 0 -02 a Learning Intentions Example Activities Cf. E • Provide opportunities for Learners to: • make comparisons between quantities and justify their choices, e. g. Which plate would you like? Why? • Use the language of quantities. E. g. David has a lot of cubes. I need more counters. Emma has fewer twigs than I do. Etc. • Use the language of quantities to compare sets of objects. Which table has more Learners sitting at it? Who has fewer sweets? Etc. • Compare quantities. • Use language of quantities to compare sets. (‘more’ , ‘a lot’, ‘fewer’, etc). • Understand that a group gets bigger when we add items to it. • Understand that a group of items gets smaller when we take away items. Key Questions • Look at the bowl of apples. Are there more green apples or red apples? How can you find out? • Are there more books on the top shelf or on the bottom shelf? How do you know? • Which set has more cubes? The set of red cubes or the set of green cubes? How do you know? Potential Barriers / Misconceptions • Learners show confusion in vocabulary- more / less. • Misconception can occur through the linking of words- the bigger a number (in 3 size) the greater it’s quantity. i. e. is bigger than 7. (worth more than…) • Learners find it challenging to identify ‘same’ and ‘different when working visually as they don’t focus on the detail. Resources Assessment Benchmark When counting objects, understands that the number name of the last object counted is the name given to the total number of objects in the group. Groups items recognising that the appearance of the group has no effect on the overall total (conservation of number).

Uses 1 -to-1 correspondence to count objects to at least 10. Language Count, collection, row, group. Cf. E MNU 0 -01 a MNU 0 -02 a Example Activities Learning Intentions • Watch me use my fingers to make a number. Raise 0 fingers. Zero! Raise 1 finger. One! Raise 2 fingers sequentially. One, two. You do that with me. Ready, One! One, two. • This time do one, two, three with me. Ready, one, two, three. Repeat for 4 & 5 fingers. This time don’t look at your fingers when you make the number. Do 3 with me. Ready, one, two, three. Check to see if you are correct. • Repeat activities for zero to five fingers. Repeat with other hand. • Use 1 -to-1 correspondence. (touches each object and gives it a number) • Represent a number using fingers (grow) • Count objects in a row. • Count objects in a group / irregular arrangement. • Count objects from a group. • Place out a row of 5 cars. Watch me count out the cars forwards & backwards. • Point to each counter in turn. Now you count the dots forwards & backwards. • Place 4 counters in a group. How many counters are there? Key Questions • Place out a group of about 10 counters. Get me 6 counters from the group. • Repeat for quantities to at least 10, varying the objects being counted and their arrangement. • Repeat activities for numbers to at least 10. Potential Barriers / Misconceptions Give me 2 of the sweets please. Some Learners may not point at or move each counter in turn – model this action for them. Learners may have difficulty coordinating a number word with each counter e. g. the may point to 2 counters when saying 'sev-en'. Some Learners may not realise that, when counting, the last number word is the answer to ‘How many? ’ Some may think that the answer to ‘How many? ’ is answered simply by pointing to each counter and counting from 1. It is important for the teacher to model identifying the quantity of the collection. Some Learners may not realise that the task of getting items from a group involves separating some items from the initial group. This realisation is referred to as having ‘pull-out’ strategy. Lots of teacher modelling will be useful building up the values required each time. Resources • Can you show me 4 fingers? Can you show me with your other hand? • The birthday card has a 4 on it. Can you put the right number of candles on the birthday cake? • How many Learners are lined up? • How many buttons are there? You can move them as you count. Can you give me 6 of the buttons? • Can you bring me five aprons from the pegs? Assessment Benchmark Uses one-to-one correspondence to count a given number of objects to at least 20. When counting objects, understands that the number name of the last object counted is the name given to the total number of objects in the group.

Uses 1 -to-1 correspondence to count a given number of objects to at least 20. Language Count, collection, row, group. Cf. E MNU 0 -01 a MNU 0 -02 a Example Activities Learning Intentions • Place out a row of 12 cars. Watch me count out the cars forwards & backwards. • Point to each counter in turn. Now you count the dots forwards & backwards. • Use 1 -to-1 correspondence. (touches each object and gives it a number) • Count objects in a row. • Count objects in a group / irregular arrangement. • Count objects from a group. • Count objects, actions & sounds (without touching). • Use and understand ordinal numbers. • • Place 15 counters in a group. How many counters are there? Place out a group of about 20 counters. Get me 13 counters from the group. Repeat for quantities to at least 20, varying the objects and their arrangement. Repeat but have the Learners point to each object rather than touch. How many oranges? Can you give me 12 oranges from the group. Can you check? • Watch me as I move my hand. Move hand in a chopping motion 3 times. 1, 2, 3. • Use your fingers to keep track of how many times I move my hand. Move hand x times. How many times was that? • This time, I will say a number and you make that many chops. Ready, four! • Repeat for no’s to 5, progressing to no’s to at least 10. Repeat using sound (claps) as well as motion. • Listen to my pattern and see if you can copy it. Clap a 2 pattern. • Now try this one. Clap a 2 -2 pattern. Repeat for 1 -2, 2 -1, 1 -3, 3 -1, 3 -3, 2 -3, 3 -2. Try to count how many claps in my pattern. Clap a 2 -2 pattern. • Use and understand ordinal numbers. • Can you point to the 4 th car ? • Who was 2 nd in the race? Potential Barriers / Misconceptions Some Learners may not point at or move each counter in turn – model this action for them. Learners may have difficulty coordinating a number word with each counter e. g. the may point to 2 counters when saying 'sev-en'. Some Learners may not realise that, when counting, the last number word is the answer to ‘How many? ’ Some may think that the answer to ‘How many? ’ is answered simply by pointing to each counter and counting from 1. It is important for the teacher to model identifying the quantity of the collection. Some Learners may not realise that the task of getting items from a group involves separating some items from the initial group. This realisation is referred to as having ‘pull-out’ strategy. Lots of teacher modelling will be useful building up the values required each time. Resources Key Questions • How many buttons can you count (row & group)? • How many Learners are in the line? • Can you take out 12 pencils from the tub? • How many windows are there on this house? • Can you count the number of claps / rings of the bell / jumps in the air, etc? • Make a line of toy cars. Can you make the second car yellow and the fifth car red? Assessment Benchmark Uses one-to-one correspondence to count a given number of objects to at least 20. Uses ordinal numbers in real life contexts, for example, ‘I am third in theline’, including the language of before, after and inbetween.

Counts in jumps (skip counts) in 2 s, 5 s and 10 s and begins to use this as a useful strategy to find how many in a larger group. Language skip count, twos, fives, tens. Cf. E Example Activities MNU 0 -02 a MNU 0 -03 a Learning Intentions • Skip count in 2 s. • Skip count in 5 s. • Skip count in 10 s. Provide opportunities for Learners to: • Skip count in 2 s. Key Questions • Skip count in 5 s. • Skip count in 10 s. Potential Barriers / Misconceptions • Learners unable to place objects in equal groups. • Not secure with one to one correspondence counting in ones, therefore will be unable to count pairs accurately. • When counting orally in 10 s: 60, 70, 80 follow a regular pattern which link to single digit numbers however 10, 20, 30 do not. • Conceptual understanding of ‘same’ and ‘different’ is not secure (both language and concept). Resources • Can you give everyone two biscuits from the jar? Can you count them out? • Can you count the spots on each side of your butterfly? Does it have an equal number of spots on each side? • I will clap where there is a number missing. 1, (clap), 3, (clap) 5. Can you tell me the missing number? • Repeat for multiples of 5 and 10. • How many eggs are there in the box? How are they arranged? (in 2 s) • Count these pairs of socks. How many pairs are there? How many socks are there altogether? • Everyone hold up one hand. Can we count the fingers? “ 5, 10, 15, …”? . Now hold up 2 hands. Assessment Benchmark Counts in jumps (skip counts) in 2 s, 5 s and 10 s and begins to use this as a useful strategy to find how many in a larger group.

Partitions single digit numbers into two parts. Language Example Activities Finger Patterns • Show me 4. Can you make 4 in a different way? • Put your hand out in front. Show me 5 on your fingers. Put down one finger. How many does that leave? What does 4 and 1 make? Show me that on your fingers. • Repeat for all combinations to 10. Ten Frames • Place out an empty ten frame and place 4 red and 2 green counters in the squares. How many counters altogether? How many red counters? How many green counters? • Repeat with other partitions of 6. Repeat for each number to 10. • Flash a ten frame with 4 red and 3 green counters in the squares. How many counters altogether? How many red counters? How many green counters? • Repeat with other partitions of 7. Repeat for each number to 10. Potential Barriers / Misconceptions Unable to recite numbers in the correct order. Not associating number names with objects in group Unable to count without putting in line or touching. Unable to count with 1 to 1 correspondence. Not knowing the number order when counting on from any given number. When counting on from a given number, include the start number in their counting. (6+3 = 6, 7, 8 = 8) rather than 6+3=7, 8, 9 = 9) MNU 0 -02 a MNU 0 -03 a Learning Intentions • Provide opportunities for Learners to separate a group into 2 sets. E. g. How many different ways can we put 4 teddies into 2 beds? How many teddies in each? How many teddies altogether? • • • Cf. E Sets, seen, unseen, ten frame, altogether, partition, total, combine Resources • • Partition numbers visually to ten (2 sets). Identify number bonds to ten. Key Questions • How many cookies on this plate? How many on that plate? How many altogether? • I have 5 toys altogether. 3 are on the table. How many are still in the box? • How many cars can you see in the picture? Can you tell me without counting? Can you see smaller groups of cars in the picture? What can you see? How many different ways can you see 6? • There are five birds in the nest. One flew off. How many are there now? • We have four aprons. There are seven Learners who want to paint. How many more aprons do we need? Assessment Benchmark Partitions single digit numbers into two or more parts and recognises that this does not affect the total, for example, �� +�� = �� and �� +�� +�� =��. Explains that zero means there is none of a particular quantity and is represented by the numeral ‘ 0’.

Partitions single digit numbers into two or more parts and recognises that this does not affect the total. Language Cf. E Sets, seen, unseen, ten frame, altogether, partition, total, combine Example Activities Learning Intentions • Provide opportunities for Learners to separate a group into 2 or more sets. E. g. How many different ways can we put 6 teddies into 3 beds? How many teddies in each? How many teddies altogether? Etc. Finger Patterns • Show me 7. 5 and 2 makes 7. Can you make 7 in a different way? 4 and 3 makes 7. How many more to make 10? 4 and 3 makes 10. • Put your hands out in front. Show me 10 on your fingers. Put down one finger. How many does that leave? What does 9 and 1 make? Show me that on your fingers. • Repeat for all combinations to 10. Challenge Learners to progress from fingers seen to fingers unseen (“bunny ears”) Ten Frames / Irregular Patterns • Place out an empty ten frame and place 4 red and 2 green counters in the squares. How many counters altogether? How many red counters? How many green counters? How many more to make 10? • Repeat with other partitions of 6. Repeat for each number to 10. • Repeat but flashing the ten frames rather than displaying. • Place out irregular patterns of items. Challenge Learners to identify how many different ways they can see the number. I can see 8. I can see 4 and 4. I can see 4 and 3 and 1. I can see 5 and 3. Etc. Potential Barriers / Misconceptions • An important goal is for Learners to visualise patterns to answer questions such as how many dots or how many empty squares. • Some Learners might attempt to count from one while visualising patterns and other Learners might ascribe a number to a group (for example, 2, 3 or 4 dots) without counting from one. Learners should be encouraged to combine and partition the patterns without counting from one. MNU 0 -02 a MNU 0 -03 a Resources • • Partition numbers visually to ten (2 or more sets). Identify number bonds to ten. Key Questions • 6 Learners are sitting at a group. 2 move to another group. How many are left? • Can you find different ways of putting 7 cubes in 3 boxes? How many altogether? • How many cars can you see in the picture? Can you tell me without counting? Can you see smaller groups of cars in the picture? What can you see? How many different ways can you see 8? • Show me 7 fingers. Can you show me a different way of making 7. How many more makes 10? Assessment Benchmark Partitions single digit numbers into two or more parts and recognises that this does not affect the total, for example, �� +�� = �� and �� +�� +�� =��. Explains that zero means there is none of a particular quantity and is represented by the numeral ‘ 0’.

Demonstrates understanding of all possible partitions of numbers to at least 10. Language Cf. E Part, whole, number bonds, partition. Example Activities Learning Intentions • Provide opportunities for Learners to identify number bonds for each number to 10 using both concrete materials and numerals. How many different ways can we put 5 cookies onto 2 plates? Can you show me / draw a picture / write the number stories for all the different ways? How do you know you have found them all? whole part 5 5 + 0 whole part 4 5 + 1 whole part 3 5 + 2 part 2 5 + 3 Etc. Learners should therefore be able to identify and write the following number bonds: • 2 + 3 = 5 • 5 + 0 = 5 • 1 + 4 = 5 • 4 + 1 = 5 • 3 + 2 = 5 • 0 + 5 = 5 • Number bonds can be explored using finger patterns, tens frames and double sided counters. • Show me 4. Show me a different 4, etc. • Show me 6. How many more makes 10? Here are 5 double sided counters. Throw them onto the table. How many red? How many yellow? Potential Barriers / Misconceptions • • MNU 0 -02 a MNU 0 -03 a Unable to recite numbers in the correct order. Not associating number names with objects in group Unable to count without putting in line or touching. Not being able to ‘hold’ the number they started with when adding the second group. Not knowing the number order when counting on from any given number. Don’t associate number facts e. g 13+4=17 and 17 -4=13 as they don’t see + and – as inverse. When counting on from a given number, include the start number in their counting. (6+3 = 6, 7, 8 = 8) rather than 6+3=7, 8, 9 = 9) Throw them again. How many different ways can they land? Resources • Identify number bonds to ten. Key Questions • How many different ways can you put 6 teddies in 2 boxes? • Can you write a number sentence for each? • How do you know you have found them all? • Can you roll a 7 using 2 dice? How many different ways could you roll 7? • Show me 6 fingers. How many more fingers to make 10? • There were 10 sweets in this packet. I have eaten 3. How many are left? • This bag contains 8 cubes. They can be blue or red. How many of each colour could there be? Assessment Benchmark Demonstrates understanding of all possible partitions of numbers to at least 10, for example, 4 can be partitioned into �� +�� , �� +�� and �� +��.

Using concrete resources , solves problems that involve addition and subtraction. Language Example Activities add, more, make, altogether, how many more? How many left? , difference, take away, leave. Cf. E MNU 0 -02 a MNU 0 -03 a Learning Intentions Provide opportunities for Learners to: • Find the total number of objects in 2 sets (rows & groups). E. g. 3 paper plates can be used to represent part, whole. Learners move the cars together into one group to find the total. • • Find the total number of items after some are taken away. Encourage Learners to count with 1 -to-1 correspondence. How many cars are left if 2 drive away? • • • Find the total number of items in 2 groups by counting all of them (counts from 1). Find how many are left when some are taken away. Understand that when counting a group the last number represents the total amount. Solve part-whole problems using concrete resources (addition & subtraction type problems). 1 2 3 4 5 6 Key Questions • Count sets aloud with 1 -to-1 correspondence in order to identify the total as being the last number spoken. • I am going to add 1 more button to this set of four buttons. How many will there be then? • Solve part-whole problems where the unknown is either the whole or part using • Show me five fingers using both your hands. Show concrete materials. E. g. If I have 3 sweets and you have 2 sweets, how many do we have me another way. altogether? If you have 5 sweets and you eat 2 of them, how many do you have left? • There are four balls in the bag. Put two more balls in the bag. How many balls altogether? • I have two carrots in a bowl. I add two more carrots to the bowl. How many altogether? • Find all the dominoes that have a total of five spots. • Show me 3 fingers on one hand. Show me 5 on the Potential Barriers / Misconceptions Resources other hand. How many fingers altogether? • Unable to recite numbers in the correct order. • I have hidden two cups in this box. There are three • Not associating number names with objects in group. on the table. How many cups are there altogether? • Unable to count without putting in line or touching. • How many different ways can we put five sweets on • Not being able to ‘hold’ the number they started with when adding the two plates? second group. • Not being able to ‘hold’ the number they started with when adding the second group. Assessment • Not knowing the number order when counting backwards. Benchmark • Learners unable to relate subtraction to taking away. Teach other phrases Counts on and back in ones to demonstrate for ‘taking away’ e. g. ‘How many less? ’ understanding of addition and subtraction. • Misunderstanding of ‘one less’; do not consistently identify the number Uses one-to-one correspondence to count a before a given number. X X given number of objects to at least 20.

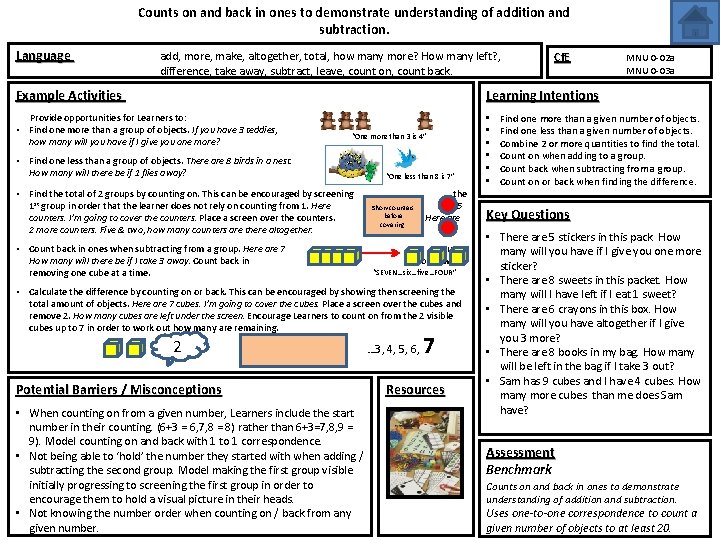
Counts on and back in ones to demonstrate understanding of addition and subtraction. Language add, more, make, altogether, total, how many more? How many left? , difference, take away, subtract, leave, count on, count back. Example Activities • Find one less than a group of objects. There are 8 birds in a nest. How many will there be if 1 flies away? “One less than 8 is 7” • Find the total of 2 groups by counting on. This can be encouraged by screening the 1 st group in order that the learner does not rely on counting from 1. Here are 5 Show counters before counters. I’m going to cover the counters. Place a screen over the counters. Here are covering. 2 more counters. Five & two, how many counters are there altogether. • Count back in ones when subtracting from a group. Here are 7 cubes. How many will there be if I take 3 away. Count back in ones while “SEVEN…six…five…FOUR” removing one cube at a time. • Calculate the difference by counting on or back. This can be encouraged by showing then screening the total amount of objects. Here are 7 cubes. I’m going to cover the cubes. Place a screen over the cubes and remove 2. How many cubes are left under the screen. Encourage Learners to count on from the 2 visible cubes up to 7 in order to work out how many are remaining. Potential Barriers / Misconceptions • When counting on from a given number, Learners include the start number in their counting. (6+3 = 6, 7, 8 = 8) rather than 6+3=7, 8, 9 = 9). Model counting on and back with 1 to 1 correspondence. • Not being able to ‘hold’ the number they started with when adding / subtracting the second group. Model making the first group visible initially progressing to screening the first group in order to encourage them to hold a visual picture in their heads. • Not knowing the number order when counting on / back from any given number. MNU 0 -02 a MNU 0 -03 a Learning Intentions Provide opportunities for Learners to: • Find one more than a group of objects. If you have 3 teddies, “One more than 3 is 4” how many will you have if I give you one more? 2 Cf. E … 3, 4, 5, 6, 7 Resources • • • Find one more than a given number of objects. Find one less than a given number of objects. Combine 2 or more quantities to find the total. Count on when adding to a group. Count back when subtracting from a group. Count on or back when finding the difference. Key Questions • There are 5 stickers in this pack. How many will you have if I give you one more sticker? • There are 8 sweets in this packet. How many will I have left if I eat 1 sweet? • There are 6 crayons in this box. How many will you have altogether if I give you 3 more? • There are 8 books in my bag. How many will be left in the bag if I take 3 out? • Sam has 9 cubes and I have 4 cubes. How many more cubes than me does Sam have? Assessment Benchmark Counts on and back in ones to demonstrate understanding of addition and subtraction. Uses one-to-one correspondence to count a given number of objects to at least 20.

Use appropriately the mathematical symbols +, -, =. Translate a word problem into a number sentence. Language number sentence, add, plus, more, and, make, sum, total, altogether, how many more? , take Cf. E (away), leave, how many are left/left over? difference between, is the same as, equal to. Example Activities Provide opportunities for Learners to: • Read and demonstrate understanding of +, - & = symbols. Can you point to the = symbol? What does this number sentence say? Can you act out this number sentence using the cubes? • Solve addition number sentences using concrete materials. Can you use the counters to show me that 4 + 3 = 7? Can you use the cubes to work out what five plus three equals? Can you write out the number sentence? “ 4 + 3 = 7” “ 5 + 3 = 8” • Solve subtraction number sentences using concrete materials. Can you use the counters to show me that 7 - 3 = 4? Can you use the cubes to work out what eight take away three equals? Can you write the number sentence? “ 7 - 3 = 4” “ 8 - 3 = 5” • Translate a word problem into a number sentence and make up a word problem using a number sentence. 5 cars are parked in a car park and 3 drive away. How many are left? Can you use the counters to show me this problem? Can you write out the number sentence for this problem? Can you make up a word problem to demonstrate the number sentence 6 + 2 = ? • Match number sentences with word problems. Which number sentence matches with the following problem? Tom has 5 stickers. His brother gives him 4 more stickers. How many stickers does he have now? 4 + 5 = 9 9 – 5 = 4 5 + 4 = 9 9 – 4 = 5 Potential Barriers / Misconceptions • Learners don’t understand the commutativity of 3+7 = 7+ 3. • Learners don’t associate number facts e. g. 13 + 4 = 17 and 17 – 4 = 13 as they don’t see + and – as inverse. • Learners struggle to match word problems with associated number sentences. Encourage Learners to act out both word problems and number sentences using concrete materials. • When counting on from a given number, include the start number in their counting. (6+3 = 6, 7, 8 = 8) rather than 6+3=7, 8, 9 = 9). Model counting on using 1 to 1 correspondence with both the first set visible progressing to screened. MNU 0 -02 a MNU 0 -03 a Learning Intentions • • Recognise and read + , - and = symbols. Read an addition / subtraction number sentence. Solve an addition / subtraction number sentence. Translate a word problem into a number sentence. Key Questions • “ 6 + 5 = 11” Can you act out this number sentence using the cubes? • Finn has 7 sweets and eats 4 of them. How many does he have left? Can you act out the problem with the cubes? Can you write a number sentence? • Can you match the word problems with the number sentences? • “ 12 – 4 = 8” Can you make up a word problem that matches with this number sentence? Resources Assessment Benchmark Use appropriately the mathematical symbols +, -, =.

Links number families when explaining mental strategies for addition & subtraction. Language part, whole, altogether, total, plus, add, more, subtract, take away, Cf. E difference, how many left, how many more, missing number, number sentence. Example Activities Provide opportunities for Learners to: • use part-whole model solve problems finding either a part or the whole. A screen can be used to cover the unknown. Sarah has 3 cookies on one plate and 2 cookies on another. How many cookies does she have altogether? whole part 3 ? + 2 Mo has 5 cookies. He eats some cookies and now he has 3 left. How many cookies did he eat? whole part 3 + • Use part-whole relationships to identify linked number sentences. What number sentences can you tell me using the following? whole 5 plus 2 equals 7 2 plus 5 equals 7 7 take away 5 equals 2 7 take away 2 equals 5 part whole part 5 7 2 NB. Learners can identify related number families and demonstrate this using concrete materials, written diagrams, written number sentences or verbally. • Solve missing number equations using concrete resources, knowledge of number bonds, etc. 5 + ● = 9. What is ●? Potential Barriers / Misconceptions • Learners will typically count from 1 to count the screened collection by making a sequence of pointing actions over the screen. Learners may require the teacher to model this action. • Learners don’t understand the commutativity of 3+7 = 7+ 3. • Not associating number names with objects in group. • Unable to count without putting in line or touching. • Not being able to ‘hold’ the number they started with when adding the second group. • Not knowing the number order when counting on from any given number. • Learners unable to relate subtraction to taking away. Teach other phrases for ‘taking away’ e. g. ‘How many less? ’ Learning Intentions • • Combine two quantities to find the total. Partition numbers into part, whole. Use part-whole relationships to find linked number sentences. Solve missing number problems. Key Questions 5 ? MNU 0 -02 a MNU 0 -03 a Resources • Connie had 5 marbles. Juan gave her 8 more marbles. How many marbles does Connie have altogether? • Finn has 6 sweets. Megan gives him some more sweets. Now he has 11 sweets. How many did Megan give him? • Mark had some money. His mum gave him £ 5 more. Now he has £ 12. How much did he start with? • Elsa had 8 cookies. She ate 3 of them. How many did she have left? • 9 birds were on a wire. Some flew away. Then there were 6 left. How many flew away? • Some Learners were playing football. 3 left the game. There were 7 left. How many were playing to begin with? Assessment Benchmark Links ‘number families’ when explaining mental strategies for addition and subtraction, for example, �� +�� =�� , �� −�� =�� and �� −�� =��. Solves simple missing number equations, for example, �� + � = ����

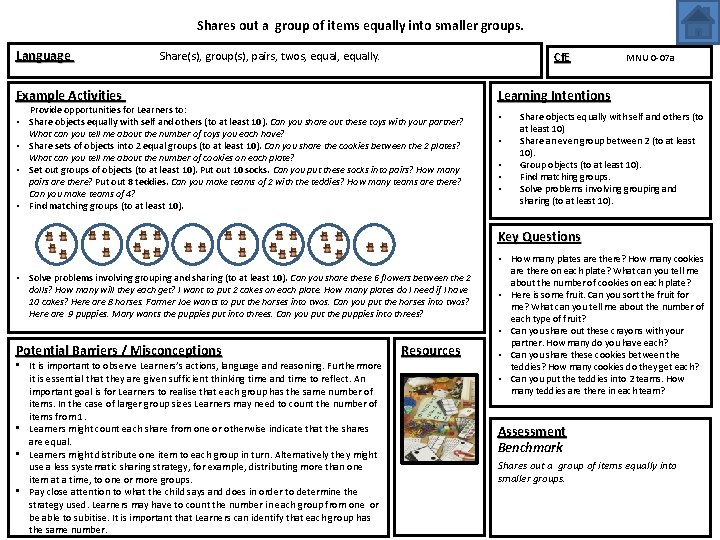
Shares out a group of items equally into smaller groups. Language Share(s), group(s), pairs, twos, equally. Example Activities Cf. E Provide opportunities for Learners to: • Share objects equally with self and others (to at least 10). Can you share out these toys with your partner? What can you tell me about the number of toys you each have? • Share sets of objects into 2 equal groups (to at least 10). Can you share the cookies between the 2 plates? What can you tell me about the number of cookies on each plate? • Set out groups of objects (to at least 10). Put out 10 socks. Can you put these socks into pairs? How many pairs are there? Put out 8 teddies. Can you make teams of 2 with the teddies? How many teams are there? Can you make teams of 4? • Find matching groups (to at least 10). MNU 0 -07 a Learning Intentions • • • Share objects equally with self and others (to at least 10) Share an even group between 2 (to at least 10). Group objects (to at least 10). Find matching groups. Solve problems involving grouping and sharing (to at least 10). Key Questions • Solve problems involving grouping and sharing (to at least 10). Can you share these 6 flowers between the 2 dolls? How many will they each get? I want to put 2 cakes on each plate. How many plates do I need if I have 10 cakes? Here are 8 horses. Farmer Joe wants to put the horses into twos. Can you put the horses into twos? Here are 9 puppies. Mary wants the puppies put into threes. Can you put the puppies into threes? Potential Barriers / Misconceptions • It is important to observe Learners’s actions, language and reasoning. Furthermore it is essential that they are given sufficient thinking time and time to reflect. An important goal is for Learners to realise that each group has the same number of items. In the case of larger group sizes Learners may need to count the number of items from 1. • Learners might count each share from one or otherwise indicate that the shares are equal. • Learners might distribute one item to each group in turn. Alternatively they might use a less systematic sharing strategy, for example, distributing more than one item at a time, to one or more groups. • Pay close attention to what the child says and does in order to determine the strategy used. Learners may have to count the number in each group from one or be able to subitise. It is important that Learners can identify that each group has the same number. Resources • How many plates are there? How many cookies are there on each plate? What can you tell me about the number of cookies on each plate? • Here is some fruit. Can you sort the fruit for me? What can you tell me about the number of each type of fruit? • Can you share out these crayons with your partner. How many do you have each? • Can you share these cookies between the teddies? How many cookies do they get each? • Can you put the teddies into 2 teams. How many teddies are there in each team? Assessment Benchmark Shares out a group of items equally into smaller groups.

Doubles numbers to a total of at least 10. Language Cf. E Twos, threes, fours, fives, equal shares, matching, pattern. Example Activities MNU 0 -02 a MNU 0 -03 a Learning Intentions Provide opportunities for Learners to: • Find matching groups. Can you find the 2 sevens? • Double quantities of objects to at least to 5. How many dots altogether? Can you double the cookies on the first plate? How many cookies now? • Make doubles using finger patterns. Put your hands out in front. Make two on your right hand. Make two on your left hand. How many altogether? Say after me - 2 and 2 makes 4. Repeat for other doubles. • Now try with your hands on your head (fingers unseen). • Similarly for 3 & 3, 4 & 4, 5 & 5, 0 & 0 and 1 & 1. • Count and make patterns of 2 (to at least 5)– pairs of socks, pairs of shoes, pairs of gloves, pairs of animals, talking partners, etc. How many pairs of socks? How many socks altogether? • Double numbers to 5. Double 5 is ten. How many wheels on 2 cars? • • • Find matching groups (to at least 5). Double quantities of objects (to at least 5). Make doubles using finger patterns. Count patterns of 2. Double numbers to 5. Solve problems involving doubles. Key Questions • How many fingers am I holding up altogether if I hold up 2 on this hand? • Can you show me 3 and 3? How many altogether? • How many gloves are there altogether if I have 4 pairs? • How many dominoes will we need if we are to get 5 each? Double 3 is six. • Solve problems involving doubles. How many sweets will we need altogether if we are to get 3 each? Potential Barriers / Misconceptions • Learners unable to place objects in equal groups. • Not secure with one to one correspondence counting in ones, therefore will be unable to count pairs accurately. • Conceptual understanding of ‘same’ and ‘different’ is not secure (both language and concept). • Learners confuse doubling with adding two. Resources Assessment Benchmark Doubles numbers to a total of at least 20 mentally, for example, �� + �� = ����.

Shares out a group of items equally into smaller groups. Finds the total of equal groups. Language Cf. E Share(s), group(s), pairs, twos, threes, fours, etc. odd, even, array. Example Activities Learning Intentions Provide opportunities for Learners to: • Share objects equally into 2 equal groups (to at least 20). Can you share out these coins between the 2 purses? How many coins do they each have? • Share sets of objects into 3+ equal groups (to at least 20). Can you share the cookies between the 5 plates? How many cookies are there on each plate? • Set out groups of objects (to at least 20). Put out 12 decorations and some cakes. Each cake that we make has to have 3 decorations on it. How many cakes can we decorate? • Identify odd and even numbers. Learners need experience of visualising what it means to be odd or even rather than rote learning the sequence of numbers. • What do you notice when we make these numbers using numicon, tens frames or unifix cubes? • Find the total of equal groups. How many groups of bears? How many bears in each group? 4 + 4 = 12, 3 fours = 12, 4 groups of 3 = 12 How many pairs can we make if we have 7 socks? Objects that can be counted in pairs are even. Objects that can’t be counted in pairs are odd. • Place objects into arrays. Can you put the eggs into equal rows? How many eggs in each row? How many altogether? So, 2 lots of 6 equals 12 or 6 + 6 = 12. Potential Barriers / Misconceptions • Learners might count each share from one or otherwise indicate that the shares are equal. • Learners might distribute one item to each group in turn. Alternatively they might use a less systematic sharing strategy, for example, distributing more than one item at a time, to one or more groups. • Pay close attention to what the child says and does in order to determine the strategy used. Learners may have to count the number in each group from one or be able to subitise. It is important that Learners can identify that each group has the same number. • Learners inaccurate when displaying arrays of cubes/objects and so pattern is not clear. • Link not clear between the array and the seemingly abstract number given as the Resources • • • MNU 0 -07 a Solve division problems by sharing equally (to at least 20). Solve division problems by grouping (to at least 20). Identify odd and even (to at least 20). Find the total of equal groups using repeated addition. Place objects into arrays. Key Questions • Can you share these biscuits between 3 people? How many biscuits each? How many altogether? • Can you share out the pencils equally so that each pot has the same amount? How many in each pot? How many altogether? • Can you put these stickers into fours? How many groups of four stickers can you make? How many altogether? • Can these 9 socks be put into pairs? What can you tell me about the number 9? Assessment Benchmark Shares out a group of items equally into smaller groups.

Doubles numbers to a total of at least 20. Language Twos, threes, fours, fives, etc, equal shares, matching, pattern, counting on. Cf. E Example Activities Learning Intentions Provide opportunities for Learners to: • Find matching groups. • • • Can you find the 2 sevens? How many dots altogether? • Double quantities of objects to at least to 10. Can you double the cookies on the first plate? How many cookies now? • Count and make patterns of 2 (to at least 10)– pairs of socks, pairs of shoes, pairs of gloves, pairs of animals, talking partners, etc. How many pairs of socks? How many socks altogether? • Double numbers to 10. How many legs on 2 spiders? Double 8 is sixteen. Relate the addition of doubles to counting on. 7…. 8, 9, 10, 11, 12, 13 and 14. • Solve problems involving doubles. How many sweets will we need altogether if we are to get 6 each? Potential Barriers / Misconceptions • Learners unable to place objects in equal groups. • Not secure with one to one correspondence counting in ones, therefore will be unable to count pairs accurately. • Conceptual understanding of ‘same’ and ‘different’ is not secure (both language and concept). • Learners confuse doubling with adding two. Resources MNU 0 -02 a MNU 0 -03 a Find matching groups (to at least 10). Double quantities of objects (to at least 10). Count patterns of 2. Double numbers to at least 10. Solve problems involving doubles. Key Questions Can you count the spots on each side of your butterfly? Does it have an equal number of spots on each side? How many eggs are there in the box? How are they arranged? (in 2 s) How many pairs of socks are there? How many socks are there altogether? How many buttons are there on this coat? Count them in twos. (answer- 10) How many pencils do we need altogether if we are both to have 7 each? John makes biscuits with 1 egg, 4 spoons of flour, 3 spoons of sugar, 5 spoons of milk. Lucy makes double the amount of biscuits. How much of each ingredient will she need? Assessment Benchmark Doubles numbers to a total of at least 20 mentally, for example, �� + �� = ����.

Splits a whole into at least halves and uses appropriate language. Language Cf. E half, share equally, shape, object, amount, split, break, part, whole. Example Activities Provide opportunities for Learners to: • Share objects equally into 2 equal groups. • Identify half of a shape. MNU 0 -07 a Learning Intentions • Identify half of a group of objects. • Cut (break) an object in half. • Put together halves to make whole shapes. Half of four is two. Potential Barriers / Misconceptions • Learners do not see a fraction as part of an object. Learners do not understand how to share equally. • Learners do not have 1 -1 correspondence. Learners cannot identify fair and unfair sharing. • Learners believe that sharing equally means the pieces have to look the same. • • • Share a quantity of objects between 2. Identify half of a group of objects. Identify half of a shape (object). Cut an object in half. Combine halves to make a whole. Key Questions • How many slices of bread to we need to make 4 whole sandwiches? • Can you cut this sandwich in half ? • How many eggs will fill this box? Can you give me half the eggs? • Can you cut the cake in half? How many pieces of cake are there now? • Put half the sheep in the field. • Half the ducks jumped in the pond. How many ducks in the pond? Resources Assessment Benchmark Splits a whole into smaller parts and explains that ‘equal parts’ are the same size. Uses appropriate vocabulary to describe each part, at least halves and quarters.

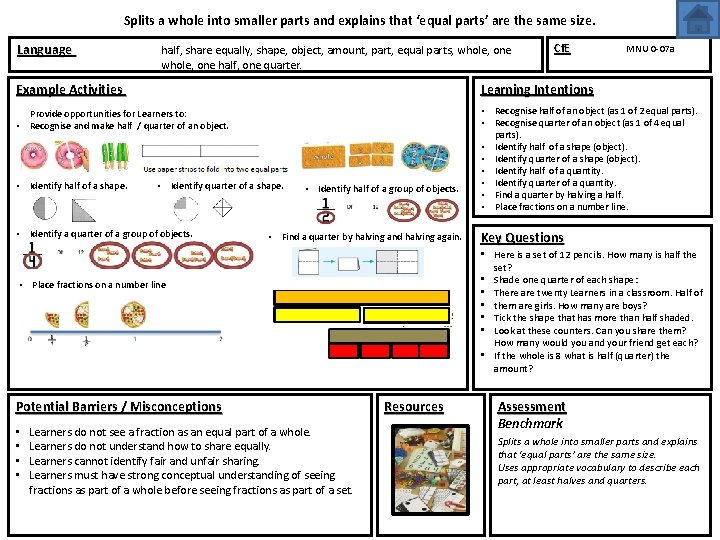
Splits a whole into smaller parts and explains that ‘equal parts’ are the same size. Language half, share equally, shape, object, amount, part, equal parts, whole, one half, one quarter. Cf. E Example Activities Learning Intentions Provide opportunities for Learners to: • Recognise and make half / quarter of an object. • • • Identify half of a shape. • Identify quarter of a shape. • Identify a quarter of a group of objects. • Identify half of a group of objects. • Find a quarter by halving and halving again. • • Learners do not see a fraction as an equal part of a whole. Learners do not understand how to share equally. Learners cannot identify fair and unfair sharing. Learners must have strong conceptual understanding of seeing fractions as part of a whole before seeing fractions as part of a set. Recognise half of an object (as 1 of 2 equal parts). Recognise quarter of an object (as 1 of 4 equal parts). Identify half of a shape (object). Identify quarter of a shape (object). Identify half of a quantity. Identify quarter of a quantity. Find a quarter by halving a half. Place fractions on a number line. Key Questions • Here is a set of 12 pencils. How many is half the set? • Shade one quarter of each shape: • There are twenty Learners in a classroom. Half of • them are girls. How many are boys? • Tick the shape that has more than half shaded. • Look at these counters. Can you share them? How many would you and your friend get each? • If the whole is 8 what is half (quarter) the amount? • Place fractions on a number line Potential Barriers / Misconceptions • • • MNU 0 -07 a Resources Assessment Benchmark Splits a whole into smaller parts and explains that ‘equal parts’ are the same size. Uses appropriate vocabulary to describe each part, at least halves and quarters.

Resources - Numerals Classroom Resources Online Resources Numeral Cards 0 to 10 Number Line Number Track

Resources - Subitising Classroom Resources Double sided counters Dice Online Resources Dominoes Irregular Array Patterns Five Frames Printed: Blank: Ten Frames Blank: Five-wise: Pair-wise: Manipulatives

Resources - Counting Classroom Resources Double sided counters Dice Online Resources Dominoes Counting Stick Range of objects for sorting & counting Range of objects for skip counting

Resources – Place Value Classroom Resources Double sided counters Dice Online Resources Dominoes Range of objects for partitioning

Resources – Addition & Subtraction Classroom Resources Double sided counters Dice Dominoes Online Resources Irregular Arrays Screen whole part

Resources – Multiplication & Division Classroom Resources Online Resources

Resources – Fractions, Decimals & Percentages Classroom Resources Online Resources