Girvan and Newman Girvan and Newman 02 04

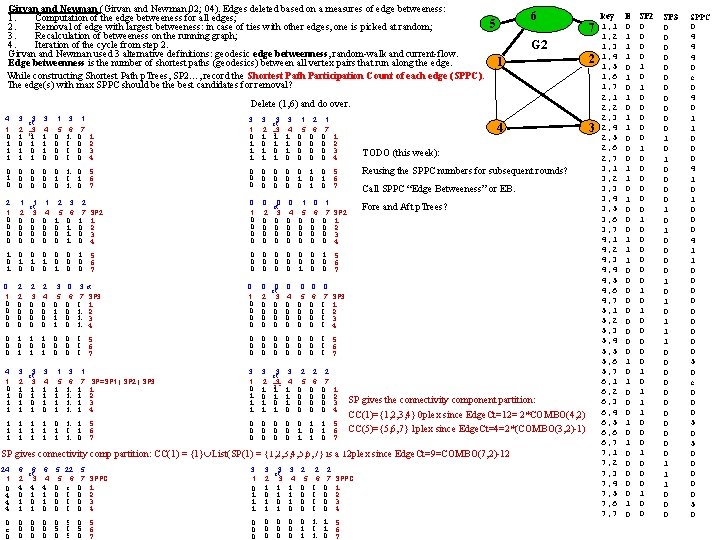
Girvan and Newman (Girvan and Newman, 02; 04). Edges deleted based on a measures of edge betweeness: 1. Computation of the edge betweeness for all edges; 5 2. Removal of edge with largest betweeness: in case of ties with other edges, one is picked at random; 3. Recalculation of betweeness on the running graph; 4. Iteration of the cycle from step 2. Girvan and Newman used 3 alternative definitions: geodesic edge betweenness, random-walk and current-flow. 1 Edge betweenness is the number of shortest paths (geodesics) between all vertex pairs that run along the edge. While constructing Shortest Path p. Trees, SP 2…, record the Shortest Path Participation Count of each edge (SPPC). The edge(s) with max SPPC should be the best candidates for removal? 6 7 G 2 2 Delete (1, 6) and do over. 4 1 3 3 2 3 3 1 ct 3 4 5 6 7 1 E 1 1 0 1 0 1 1 0 0 0 2 1 1 0 0 0 3 1 1 1 0 0 4 3 3 3 1 2 1 ct 3 4 5 6 7 1 E 1 1 0 0 0 1 4 2 0 1 1 0 0 0 2 1 1 0 0 0 3 1 1 1 0 0 4 TODO (this week): 0 0 0 1 0 5 1 0 0 0 1 6 0 0 0 1 0 7 0 0 0 1 0 5 0 0 1 0 1 6 0 0 0 1 0 7 Reusing the SPPC numbers for subsequent rounds? 2 1 1 2 Fore and Aft p. Trees? 0 0 0 0 1 ct 3 0 0 1 2 3 2 0 0 4 5 6 7 SP 2 1 2 0 0 0 0 1 1 1 1 0 0 0 1 2 3 4 1 0 0 0 1 5 0 1 1 1 0 0 0 6 1 0 0 0 1 0 0 7 0 0 0 0 2 2 2 3 0 3 ct 0 0 1 2 3 4 5 6 7 SP 3 1 2 0 0 0 0 1 1 1 0 0 0 1 1 2 3 4 0 0 0 1 0 4 5 6 0 0 0 1 7 SP 2 0 0 1 2 3 4 0 0 0 1 5 0 0 0 0 6 0 0 1 0 0 7 0 0 0 ct 3 0 0 0 0 0 4 5 6 0 0 0 0 7 SP 3 0 0 1 2 3 4 0 1 1 1 0 0 0 5 0 0 0 0 6 0 1 1 1 0 0 0 7 0 0 0 0 5 0 0 0 0 6 0 0 0 0 7 4 3 1 2 0 1 1 3 ct 3 1 1 0 1 3 1 3 4 5 6 7 SP=SP 1 | SP 2 | SP 3 1 1 0 1 1 1 1 2 3 4 1 1 0 1 1 5 1 1 1 0 1 6 1 1 1 0 7 Call SPPC “Edge Betweeness” or EB. 3 3 3 2 2 2 ct 3 4 5 6 7 1 SP 1 1 0 0 0 1 2 0 1 1 0 0 0 2 1 1 0 0 0 3 1 1 1 0 0 4 0 0 0 1 1 5 0 0 1 0 1 6 0 0 1 1 0 7 SP gives the connectivity component partition: CC(1)={1, 2, 3, 4} 0 plex since Edge. Ct=12= 2*COMBO(4, 2) CC(5)={5, 6, 7} 1 plex since Edge. Ct=4=2*(COMBO(3, 2)-1) SP gives connectivity comp partition: CC(1) = {1} List(SP(1) = {1, 2, 3, 4, 5, 6, 7} is a 12 plex since Edge. Ct=9=COMBO(7, 2)-12 24 1 0 4 4 4 6 6 ct 2 3 4 0 1 1 4 1 0 1 6 4 4 1 1 0 5 22 5 6 0 0 c 0 0 0 5 7 SPPC 0 0 1 2 3 4 0 0 0 5 c 0 0 0 5 6 0 0 0 5 0 7 3 1 3 3 ct 2 3 0 1 1 1 1 0 1 3 4 1 1 1 0 2 5 0 0 2 6 0 0 2 7 SPPC 0 0 1 2 3 4 0 0 0 1 1 5 0 0 1 0 1 6 0 0 1 1 0 7 3 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 E 0 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 0 SP 2 0 0 1 0 0 0 0 1 0 0 0 1 0 1 1 1 0 0 0 1 0 0 SP 3 0 0 0 1 0 1 0 0 0 0 1 0 1 1 1 0 0 0 1 1 1 0 0 0 SPPC 0 4 4 4 0 c 0 4 0 1 1 0 0 0 4 1 1 0 0 0 0 0 5 0 c 0 0 0 5 0

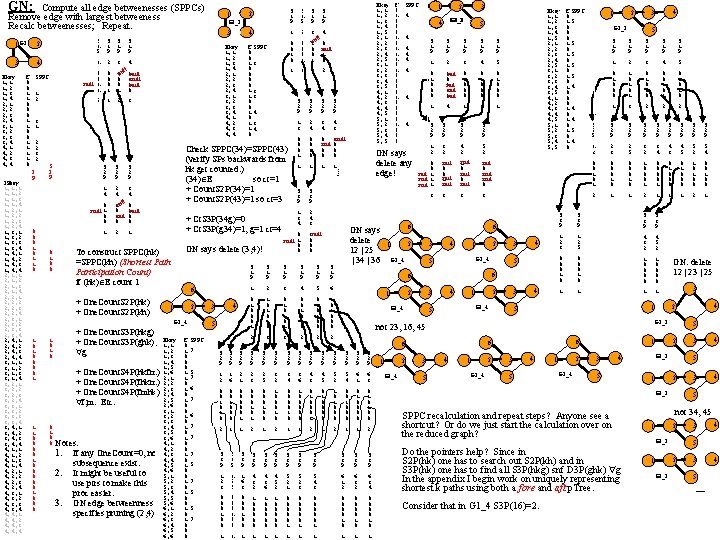
GN: Compute all edge betweenesses (SPPCs) Remove edge with largest betweeness Recalc betweenesses; Repeat. 1 G 1 3 Ekey 1, 1 1, 2 1, 3 1, 4 2, 1 2, 2 2, 3 2, 4 3, 1 3, 2 3, 3 3, 4 4, 1 4, 2 4, 3 4, 4 2 Pkey 1, 1, 1, 2 1, 1, 3 1, 1, 4 1, 2, 1 1, 2, 2 1, 2, 3 1, 2, 4 1, 3, 1 1, 3, 2 1, 3, 3 1, 3, 4 1, 4, 1 1, 4, 2 1, 4, 3 1, 4, 4 2, 1, 1 2, 1, 2 2, 1, 3 2, 1, 4 2, 2, 1 2, 2, 2, 3 2, 2, 4 2, 3, 1 2, 3, 2 2, 3, 3 2, 3, 4 2, 4, 1 2, 4, 2 2, 4, 3 2, 4, 4 3, 1, 1 3, 1, 2 3, 1, 3 3, 1, 4 3, 2, 1 3, 2, 2 3, 2, 3 3, 2, 4 3, 3, 1 3, 3, 2 3, 3, 3, 4, 1 3, 4, 2 3, 4, 3 3, 4, 4 4, 1, 1 4, 1, 2 4, 1, 3 4, 1, 4 4, 2, 1 4, 2, 2 4, 2, 3 4, 2, 4 4, 3, 1 4, 3, 2 4, 3, 3 4, 3, 4 4, 4, 1 4, 4, 2 4, 4, 3 4, 4, 4 E 0 0 1 1 0 2 S 1 P 4 1 2 3 0 0 null 1 1 0 0 0 1 1 null 0 2 1 2 3 SPPC 0 0 1 2 0 0 0 3 1 0 0 2 2 3 2 0 S 2 2 P P 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 S 2 P 1 4 2 4 0 null 1 0 0 1 3 4 + Ct. S 3 P(34 g)=0 + Ct. S 3 P(g 34)=1, g=1 ct=4 1 GN says delete (3, 4)! To construct SPPC(hk) =SPPC(kh) (Shortest Path Participation Count) if (hk) E count 1 6 2 1 G 1_4 + One. Count. S 3 P(hkg) + One. Count. S 3 P(ghk), g + One. Count. S 4 P(hkfm) + One. Count. S 4 P(fhkm) + One. Count. S 4 P(fmhk) f, m. Etc. Notes: 1. If any One. Count=0, no subsequence exist. 2. It might be useful to use ptrs to make this proc easier. 3. GN edge betweenness specifies pruning (2, 4) E SPPC 00 00 13 02 00 00 00 13 13 00 00 14 01 13 14 00 S 1 P 1 2 3 0 0 1 1 1 2 Ekey 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 E 0 1 0 0 0 1 1 0 1 0 1 0 0 1 0 0 0 4 3 5 SPPC 0 7 0 0 5 7 0 6 4 7 0 6 0 7 0 4 7 0 5 0 7 0 5 5 7 2 S 2 P 1 3 2 4 3 4 4 3 0 0 0 1 null 0 0 0 1 1 3 3 S 3 P 1 3 4 2 4 3 0 null 1 0 0 GN says delete any edge! GN says delete 12 | 25 | 34 | 36 1 null 0 0 0 S 1 P S 1 P 1 2 3 4 5 6 0 1 0 0 0 1 1 0 1 0 1 0 0 1 0 0 0 2 3 3 2 2 2 S 1 P 1 2 3 4 5 0 1 0 0 0 1 nul 0 1 0 0 0 1 4 1 1 1 S 2 P S 2 P S 2 P 1 2 1 6 2 1 2 3 2 5 3 2 3 4 3 6 4 3 4 5 5 2 5 4 6 1 6 3 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 5 S 1 P 1 2 3 4 5 0 1 0 0 0 1 0 1 0 1 3 2 2 2 S 2 P S 2 P S 2 P 1 2 2 3 2 5 3 2 3 4 4 3 4 5 5 2 5 4 S 2 P 1 2 3 2 4 2 5 2 1 nul 0 0 1 nul 1 nul 0 0 0 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 0 3 3 3 2 1 1 1 2 1 4 4 3 2 1 G 1_4 5 6 4 3 G 1_4 5 4 3 2 1 S 3 P 1 2 3 1 2 5 4 3 2 4 5 2 0 0 0 1 0 1 0 0 0 0 1 1 2 1 1 S 3 P S 3 P S 3 P 1 2 3 1 2 5 1 6 3 4 3 2 4 3 6 4 5 2 1 5 2 3 5 4 3 6 1 2 6 3 4 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 1 1 2 2 1 G 1_4 5 4 2 1 G 1_4 3 4 5 2 1 G 1_4 3 G 1_3 4 5 2 1 Do the pointers help? Since in S 2 P(hk) one has to search out S 2 P(kh) and in S 3 P(hk) one has to find all S 3 P(hkg) snf D 3 P(ghk) g In the appendix I begin work on uniquely representing shortest k paths using both a fore and aft p. Tree. Consider that in G 1_4 S 3 P(16)=2. 3 4 5 G 1_3 SPPC recalculation and repeat steps? Anyone see a shortcut? Or do we just start the calculation over on the reduced graph? 4 5 2 1 6 6 3 3 2 1 5 GN: delete 12 | 23 | 25 G 1_3 6 S 2 P 2 G 1_3 S 1 P S 2 P 5 2 4 3 2 1 S 2 P 3 G 1_4 E SPPC 00 15 00 00 00 15 04 15 00 14 00 00 04 14 00 15 00 14 00 not 23, 16, 45 S 2 P 1 S 1 P 6 2 1 Ekey 1, 1 1, 2 1, 3 1, 4 1, 5 2, 1 2, 2 2, 3 2, 4 2, 5 3, 1 3, 2 3, 3 3, 4 3, 5 4, 1 4, 2 4, 3 4, 4 4, 5 5, 1 5, 2 5, 3 5, 4 5, 5 5 S 1 P 0 0 nul 1 G 1_4 S 2 P 1 4 6 1 S 2 P 2 G 1_2 6 S 2 P 1 3 2 1 3 S 1 P 2 SPPC 0 4 0 0 0 4 4 4 0 0 0 0 4 0 0 0 E 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 Ekey 1, 1 1, 2 1, 3 1, 4 1, 5 2, 1 2, 2 2, 3 2, 4 2, 5 3, 1 3, 2 3, 3 3, 4 3, 5 4, 1 4, 2 4, 3 4, 4 4, 5 5, 1 5, 2 5, 3 5, 4 5, 5 S 1 P 4 ull 1 n 0 0 1 null 0 1 1 0 Check SPPC(34)=SPPC(43) (verify SPs backwards from hk get counted. ) (34) E so ct=1 + Count. S 2 P(34)=1 + Count. S 2 P(43)=1 so ct=3 S 2 P + One. Count. S 2 P(hk) + One. Count. S 2 P(kh) 4 Ekey 1, 1 1, 2 1, 3 1, 4 2, 1 2, 2 2, 3 2, 4 3, 1 3, 2 3, 3 3, 4 4, 1 4, 2 4, 3 4, 4 3 4 l l 1 nu 0 0 1 null 1 nul 0 0 0 2 G 1_1 S 1 P ll 2 1 3 4 5 not 34, 45 2 1 G 1_3 4 5 2 1 3 3 5 4

1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 2 1 0 1 1 0 0 0 0 0 1 0 0 0 3 4 1 E 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 0 0 0 5 1 0 0 0 0 0 0 0 0 6 1 0 0 0 0 0 0 0 0 0 0 7 1 0 0 0 1 1 0 0 0 0 0 0 0 8 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 9 10 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 0 3 1 0 0 0 0 0 0 0 0 4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 1 0 0 0 1 0 0 1 1 1 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 1 1 0 1 0 1 0 1 1 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 1 0 0 0 1 1 1 0 0 1 1 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 5 6 7 8 9 20 1 2 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 1 1 1 0 1 3 0 0 0 0 0 0 0 1 0 1 0 0 1 1 4 5 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 7 8 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 1 9 0 0 0 0 0 0 1 0 0 0 1 1 30 0 1 0 0 0 0 0 0 0 1 1 1 2 1 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 3 4 0 0 0 0 1 1 1 0 1 1 0 0 1 1 0 0 0 1 1 1 1 1 1 0 1 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 1 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 0 0 0 0 1 11 12 13 14 05 06 07 08 09 00 01 02 03 04 15 16 07 08 09 00 01 02 03 04 0 0 1 1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 0 0 0 01 02 03 04 15 16 17 18 09 00 11 12 13 04 05 06 07 18 09 00 01 12 03 04 05 06 07 08 09 00 01 02 13 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 2 1 0 1 1 0 0 0 0 0 1 0 0 0 34 EB 4 5 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 6 1 0 0 0 0 0 0 0 0 0 0 7 1 0 0 0 1 1 0 0 0 0 0 0 0 8 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 9 10 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 0 3 1 0 0 0 0 0 0 0 0 4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 5 6 7 8 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 9 20 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 3 0 0 0 0 0 0 0 1 0 1 0 0 1 1 4 5 6 7 8 9 30 1 2 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 1 1 1 0 3 0 0 0 0 1 1 1 0 1 1 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 To construct SPPC(hk) if (hk) E count 1 + One. Count. S 2 P(hk) + One. Count. S 2 P(kh) + One. Count. S 3 P(hkg) + One. Count. S 3 P(ghk) + One. Count. S 4 P(hkfm) + One. Count. S 4 P(fhkm) + One. Count. S 4 P(fmhk) 10, 25, 26, 28, 29, 31 33, 34 not shown (only 17 on, 8 only 27 turned on 8 8 8 9 10 8 8 8 8 10 8=4 dg 5 6 7 11 2 3 5 6 7 8 9 21 2 3 4 7 30 SP 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 15, 16, 19, 21, 23, 24, 27, 30 only 17 on, 5 deg=1 8=5 dg 17 SP 5

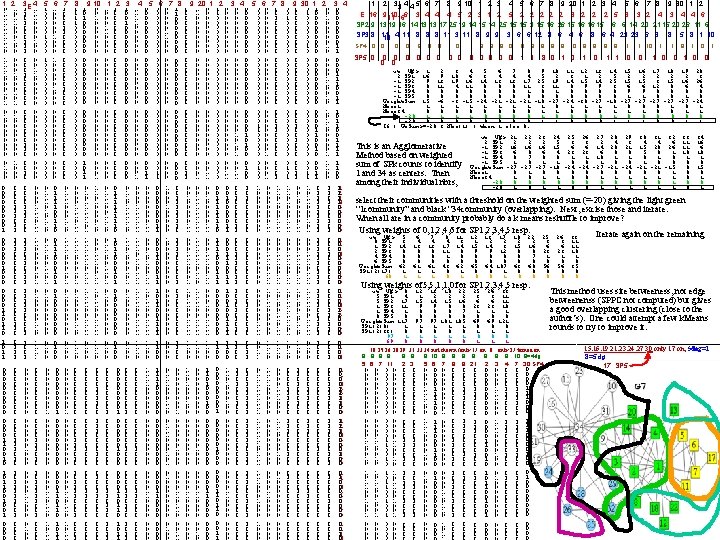
3 1 2 2 2 3 1 4 2 5 2 6 2 7 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 3 SP 2 1 4 1 5 0 6 1 7 0 0 0 0 1 0 0 0 0 0 3 SP 3 2 4 1 5 0 0 0 0 3 SP 4 1 1 2 2 0 0 0 1 0 2 ct 8 E 2 1 1 2 1 4 2 5 2 7 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 2 0 4 0 5 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 1 7 0 ct 8 2 1 1 4 2 5 2 7 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 4 0 5 0 6 0 7 0 0 0 0 0 0 0 Delete (1, 2) And {3, 6, 8} and do over. 0 ct 8 0 1 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 3 1 2 2 2 3 1 4 2 5 2 6 2 7 0 1 1 0 0 0 0 1 1 0 1 0 1 2 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 1 2 0 0 0 1 0 0 0 ct 8 1 2 ct E G 5 10 2 2 3 4 4 4 5 2 6 4 7 3 7 4 6 ct SP 2 ct SP SP gives connectivity comp partition: CC(1)={1, 5, 7} is a 0 plex since Edge. Ct=3=COMBO(3, 2)-0. CC(2)={2, 4} is a 0 plex since Edge. Ct=1=COMBO(2, 2)-0. 2 ct 8 SP 0 6 0 0 3 0 6 0 0 4 0 0 0 0 0 1 0 4 0 0 0 3 0 0 0 1 0 0 0 0 1 3 0 0 0 1 0 0 0 2 ct 8 SPPC (Shortest Path Participation Counts) 0 0 1 0 0 2 8 SP gives connectivity comp partition: CC(1)={1, 2, 4, 5, 7} is a 5 plex since Edge. Ct=5=COMBO(5, 2)-5. CC(3)={3, 6, 8} is a 0 plex since Edge. Ct=3=COMBO(3, 2)-0 12 1 1 5

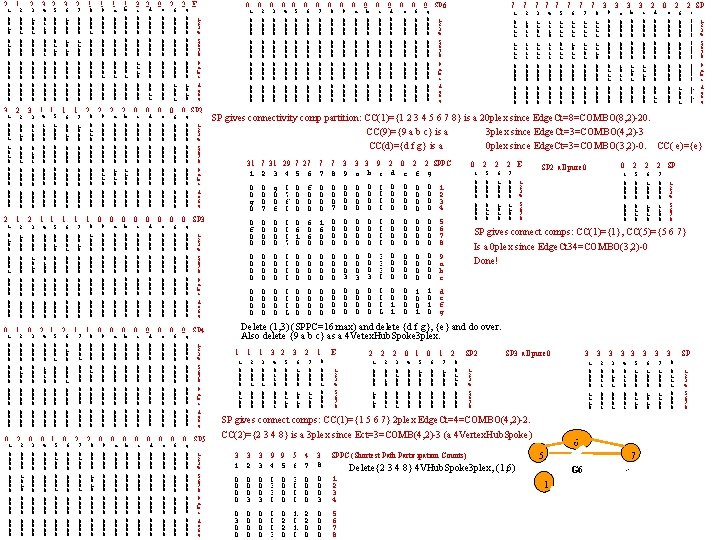
2 1 0 0 0 0 0 3 1 0 0 0 1 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 2 0 0 0 1 0 0 0 2 2 0 0 0 1 0 0 0 0 0 1 22 10 00 00 00 00 1 22 00 00 00 10 00 00 00 2 2 0 0 1 0 0 0 2 3 1 0 0 0 0 3 3 0 0 1 0 0 0 0 2 3 0 0 0 1 0 0 0 0 0 3 0 0 0 0 0 0 3 2 4 0 1 1 0 0 0 5 0 0 0 1 1 0 0 0 0 0 1 1 44 10 00 00 00 00 55 10 00 00 00 00 1 1 4 0 0 0 1 0 0 0 0 0 5 0 0 0 1 0 0 0 0 2 1 4 0 0 0 1 0 0 0 0 0 5 0 0 1 0 0 0 0 1 4 0 0 0 0 5 0 1 0 0 0 0 3 6 1 0 0 0 0 0 1 6 0 0 0 1 0 0 0 0 1 6 0 0 1 0 0 0 2 6 0 0 1 0 0 0 0 6 0 0 0 0 2 7 0 0 1 1 0 0 0 0 0 1 7 0 1 0 0 0 0 1 7 0 0 0 1 0 0 0 0 1 77 00 00 00 01 00 00 00 2 7 0 1 0 0 0 0 1 8 0 0 0 1 0 0 0 2 8 0 1 0 0 0 0 1 8 0 1 0 0 0 0 1 8 0 0 0 1 0 0 0 2 8 0 0 1 0 0 0 1 9 0 0 0 1 0 0 2 99 00 00 00 10 10 00 00 0 9 0 0 0 0 0 0 0 0 0 9 0 0 0 0 1 a 0 0 0 1 0 0 2 a 0 0 0 0 1 0 0 0 0 0 0 0 a 0 0 0 0 0 0 0 0 1 b 0 0 0 1 0 0 2 b 0 0 0 0 0 1 0 0 0 0 0 0 0 b 0 0 0 0 0 0 0 0 3 2 c 0 0 0 0 1 1 1 0 0 0 d 0 0 0 0 1 1 0 0 c 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 d 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 e 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 e 0 0 0 0 2 f 0 0 0 1 0 0 1 0 f 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 E g 0 0 0 1 0 1 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 0 SP 2 g 0 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 0 SP 5 g 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 0 3 0 0 0 0 0 4 0 0 0 0 5 0 0 0 0 0 6 0 0 0 0 0 7 0 0 0 0 0 9 0 0 0 0 8 0 0 0 0 0 a 0 0 0 0 0 b 0 0 0 0 0 d 0 0 0 0 c 0 0 0 0 0 e 0 0 0 0 0 SP 6 g 0 0 0 0 f 0 0 0 0 7 7 7 1 0 1 1 1 1 0 0 0 0 2 1 0 1 1 1 0 0 0 0 3 1 1 0 1 1 1 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 31 7 31 29 7 27 7 7 3 3 3 9 2 0 2 2 SPPC 1 2 3 4 5 6 7 8 9 a b c d e f g 4 1 1 1 0 0 0 0 5 1 1 0 1 1 1 0 0 0 0 7 7 6 1 1 1 0 0 0 0 7 3 3 9 0 0 0 0 0 1 1 1 0 0 8 1 1 1 1 0 0 0 0 0 7 1 1 1 0 1 0 0 0 0 3 3 b 0 0 0 0 1 1 0 0 0 0 a 0 0 0 0 1 0 1 1 0 0 2 0 d 0 0 0 0 1 1 c 0 0 0 0 1 1 1 0 0 0 2 e 0 0 0 0 2 SP g 0 0 0 1 0 f 0 0 0 1 0 0 1 1 2 3 4 5 6 7 8 9 a b c d e f g 0 0 0 0 7 g 0 0 f 0 7 f 0 0 0 0 7 0 0 0 0 0 0 0 0 1 2 3 4 0 f 0 0 0 0 7 0 6 1 0 6 0 1 6 0 0 0 0 0 0 0 0 0 0 5 6 7 8 0 0 0 0 0 0 0 0 0 3 0 0 0 3 3 0 0 0 0 0 9 a b c 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 d e f g 0 1 0 0 0 0 2 2 2 E 5 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 0 SP 2 all pure 0 1 0 0 0 0 1 2 3 4 5 6 7 8 2 2 2 SP 5 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 1 2 3 4 5 6 7 8 SP gives connect comps: CC(1)={1}, CC(5)={5 6 7} Is a 0 plex since Edge. Ct 34=COMBO(3, 2)-0 Done! Delete (1, 3) (SPPC=16 max) and delete {d f g}, {e} and do over. Also delete {9 a b c} as a 4 Vetex. Hub. Spoke 3 plex. 0 SP 4 g 0 0 0 0 2 0 0 0 0 SP gives connectivity comp partition: CC(1)={1 2 3 4 5 6 7 8} is a 20 plex since Edge. Ct=8=COMBO(8, 2)-20. CC(9)={9 a b c} is a 3 plex since Edge. Ct=3=COMBO(4, 2)-3 CC(d)={d f g} is a 0 plex since Edge. Ct=3=COMBO(3, 2)-0. CC( e)={e} 0 SP 3 g 0 0 0 0 0 1 1 0 0 0 1 2 0 0 0 1 3 0 0 0 1 0 0 3 2 4 0 1 1 0 0 1 5 0 0 0 1 1 0 3 6 1 0 0 0 1 0 2 7 0 0 1 1 0 0 1 8 0 0 0 1 0 0 E 1 2 3 4 5 6 7 8 2 1 0 0 1 0 2 2 0 0 1 2 3 0 1 0 0 0 1 4 0 0 0 0 5 1 0 0 0 0 6 0 0 0 0 1 7 1 0 0 0 0 2 SP 2 8 0 1 1 0 0 0 SP 3 all pure 0 1 0 0 1 1 1 0 1 2 3 4 5 6 7 8 SP gives connect comps: CC(1)={1 5 6 7} 2 plex Edge. Ct=4=COMBO(4, 2)-2. CC(2)={2 3 4 8} is a 3 plex since Ect=3=COMB(4, 2)-3 (a 4 Vertex. Hub. Spoke) 3 3 3 9 9 5 4 3 1 2 3 4 5 6 7 8 SPPC (Shortest Path Participation Counts) 0 0 0 3 0 3 3 0 0 0 0 3 1 2 3 4 0 3 0 0 0 0 3 0 2 2 0 1 0 2 2 0 0 0 5 6 7 8 3 2 0 0 1 1 0 0 0 1 3 3 0 1 0 0 0 1 3 3 4 0 1 1 0 0 1 5 1 0 0 1 1 0 6 5 Delete{2 3 4 8} 4 VHub. Spoke 3 plex, (1, 6) 0 0 3 4 6 1 0 0 0 1 0 3 3 8 0 1 1 1 0 0 7 1 0 0 0 1 1 0 0 SP 1 2 3 4 5 6 7 8 7 9 a 2 b c d e f g G 6 1 3 3

1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 2 1 0 1 1 0 0 0 0 0 1 0 0 0 3 4 1 E 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 0 0 0 5 1 0 0 0 0 0 0 0 0 6 1 0 0 0 0 0 0 0 0 0 0 7 1 0 0 0 1 1 0 0 0 0 0 0 0 8 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 9 10 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 0 3 1 0 0 0 0 0 0 0 0 4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 1 0 0 0 1 0 0 1 1 1 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 1 1 0 1 0 1 0 1 1 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 1 0 0 0 1 1 1 0 0 1 1 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 5 6 7 8 9 20 1 2 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 1 1 1 0 1 3 0 0 0 0 0 0 0 1 0 1 0 0 1 1 4 5 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 7 8 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 1 9 0 0 0 0 0 0 1 0 0 0 1 1 30 0 1 0 0 0 0 0 0 0 1 1 1 2 1 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 3 4 1 2 33 4 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 20 1 2 3 4 5 6 7 8 9 30 1 2 0 0 E 16 9 11 10166 3 4 4 4 5 2 3 1 2 5 2 2 2 3 2 2 2 5 3 3 2 4 3 4 4 6 0 0 SP 2 9 13 19 16 14 13 13 17 25 19 14 15 14 25 15 15 3 15 16 26 15 16 16 15 6 6 14 20 21 15 20 26 11 6 0 0 SP 3 8 11 0 10 4 11 8 8 8 11 3 11 8 9 9 3 6 6 12 8 6 4 6 8 6 4 23 23 6 8 8 5 8 1 10 0 SP 4 0 0 8 8 8 1 0 1 8 8 8 0 9 9 8 8 8 0 8 8 1 1 10 1 1 8 1 0 1 1 1 SP 5 0 0 0 0 1 1 8 0 1 0 1 1 0 0 0 0 wt V#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 2 SP 1 16 9 10 6 3 4 4 4 5 2 3 1 2 5 2 2 2 3 1 -1 SP 2 9 13 19 16 14 13 13 17 25 19 14 15 14 25 15 15 3 15 16 26 1 -1 SP 3 8 11 4 11 8 8 8 11 3 11 8 9 9 3 6 6 12 8 6 4 0 -1 SP 4 0 0 8 8 8 1 0 1 8 8 8 0 9 9 8 8 8 0 0 -1 SP 5 0 0 0 0 1 1 8 0 1 Weight. Sum 15 -6 -3 -15 -24 -21 -21 -18 -27 -24 -30 -27 -18 -27 -27 -27 -24 1 Nbrs 1 1 1 1 1 0 0 0 1 Nbrs 34 0 0 0 0 1 1 1 -20 1 1 0 0 0 0 1 -20 0 0 0 0 1 1 1 If ( Wt. Sum>=-20 & Nbr(1) ) then 1 else 0. 0 0 wt V#> 21 22 23 24 25 26 27 28 29 30 31 32 33 34 1 2 SP 1 2 2 2 5 3 3 2 4 3 4 4 6 11 16 1 This is an Agglomerative -1 SP 2 16 16 16 15 6 6 14 20 21 15 20 26 11 6 1 -1 SP 3 6 8 6 4 23 23 6 8 8 5 8 1 10 10 1 Method based on weighted -1 SP 4 8 7 8 8 1 1 10 1 1 8 1 0 1 1 -1 SP 5 1 0 1 1 0 0 1 sum of SPk counts to identify Weight. Sum -27 -27 -18 -24 -27 -21 -24 -21 -15 0 15 1 Nbrs 1 0 0 0 0 0 1 and 34 as centers. Then Nbrs 34 1 0 1 1 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 1 0 0 0 0 0 1 1 1 0 1 0 1 1 0 0 0 1 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 0 0 0 0 1 11 12 13 14 05 06 07 08 09 00 01 02 03 04 15 16 07 08 09 00 01 02 03 04 0 0 1 1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 0 0 0 01 02 03 04 15 16 17 18 09 00 11 12 13 04 05 06 07 18 09 00 01 12 03 04 05 06 07 08 09 00 01 02 13 among their individual nbrs, -20 0 1 0 0 0 1 0 1 0 1 1 1 0 0 0 1 select their communities with a threshold on the weighted sum (=-20) giving the light green “ 1 community” and black “ 34 community (overlapping). Next, excise those and iterate. When all are in a community probably do a k means reshuffle to improve? Using weights of 0, 1, 2, 4, 6 for SP 1, 2, 3, 4, 5 resp. Iterate again on the remaining wt V#> 5 0 SP 1 3 1 SP 2 14 2 SP 3 8 4 SP 4 8 6 SP 5 0 Weight. Sum 62 SP 1|2(17) 1 60 1 6 4 13 8 8 0 61 1 1 7 4 13 8 8 0 61 1 1 8 4 17 11 1 0 43 0 0 11 3 14 8 8 0 62 1 1 12 1 15 9 8 0 65 0 0 13 17 2 2 14 3 9 12 8 8 0 8 64 107 0 1 18 2 15 8 8 0 63 0 0 22 2 16 8 7 0 60 0 0 Using weights of 5, 5, 1, 1, 0 for SP 1, 2, 3, 4, 5 resp. 25 3 6 23 1 0 56 0 0 wt V#> 8 12 13 18 22 25 26 33 5 SP 1 4 1 2 2 2 3 3 11 5 SP 2 17 15 14 15 16 6 6 11 1 SP 3 11 9 9 8 8 23 23 10 1 SP 4 1 8 8 8 7 1 1 1 0 SP 5 0 0 0 0 Weight. Sum 117 97 97 101 105 69 69 121 SP 1|2(8) 1 1 1 0 0 0 SP 1|2(33) 0 0 0 1 1 1 97 1 1 1 0 0 0 69 0 0 0 1 10, 25, 26, 28, 29, 31 33, 34 not shown (only 17 on, 8 only 27 turned on 8 8 8 9 10 8 8 8 8 10 8=4 dg 5 6 7 11 2 3 5 6 7 8 9 21 2 3 4 7 30 SP 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 26 3 6 23 1 0 56 0 0 33 11 11 10 1 0 35 0 0 This method uses site betweeness, not edge betweenenss (SPPC not computed) but gives a good overlapping clustering (close to the author’s). One could attempt a few k. Means rounds to try to improve it. 15, 16, 19, 21, 23, 24, 27, 30 only 17 on, 5 deg=1 8=5 dg 17 SP 5

APPENDIX Edge, E, Path(PT), Shortest. Pathv(SPT), Acyclic. Path(APT) Trees and Cycle. List(CL) of G 1 (pred is Not. Pure. Zero) First, construct stride=|V|, 2 -level Edge p. Tree, all others are constructed concurrently from it. All are 3 hop cycles. Each has 3 E one-level E 2 -lev stri=|V|=4 PT , extension of E APT SPT 1111 E 1 key 1, 1 1, 2 1, 3 1, 4 2, 1 2, 2 2, 3 2, 4 3, 1 3, 2 3, 3 3, 4 4, 1 4, 2 4, 3 4, 4 PE 1 0 0 1 1 0 G 1 2 LEG 1 1 1 0 0 1 1 2 0 0 0 1 3 1 0 0 1 4 1 1 1 0 0 1 1 1 3 0 0 0 1 1 3 4 1 1 0 0 SPT is completed. For Big Graphs, could stop here (e. g. , Friends has ~1 B vertices but a diameter of 4, so we would only need to build PT 4 -hop paths) and possible expressed as a tree of lists rather than a tree of bitmaps. For sparse Big. Graphs, E could be leveled further and/or a tree of lists (then APT, SPT will be also). SPT(G)k (with k turned on) is mask (>0 is “yes”) for connectivity comp, COMP(G)k vk. For bitmap of COMPk bitslicing SPT (SPTk, h. . SPTk, 0 k=1. . |V| then COMPk ORj=h. . 0 SPTk, h. SPT structure may be useful as separate “categorical” bitmaps Shortest Path Length (SPk, h h=1. . H. Also keep a mask of Shortest Paths so far, SPSFk vertex, k. With each new SP bitmap, SPB, SPSFk | SPB, SPk, h+1 SPB & SPSFk. SPTgives the Connectivity Component Partition; Maximal Cliques (go across SPk, 1 then look within subsets of those k’s for commonality); Note, Cliques are 0 -plexes. Each mask, SPk, 1 masks a 1 -plex. Each SPk, 1&SPk, 2 masks a 2 plex (which is SPSFk, 2? So if we save each SPSF instead of overwriting, we have k-plex masks w/o further work? ), etc. Next construct predicates for each Path related data structures, PT APT SPSF, to make them into p. Trees on a k-path table, E, E 2, E 3, … 1 4 0 1 1 0 1 4 3 1 0 0 0 G 1 PTG 1 1 1 2 0 0 0 1 3 1 0 0 1 2 4 1 0 3 1 0 0 0 1 3 4 1 1 0 0 4 1 0 0 1 0 4 3 1 0 0 0 3 1 4 0 1 1 0 3 4 1 0 0 1 0 4 1 3 0 0 0 1 4 3 1 0 0 0 1 2 4 1 0 0 1 0 2 4 3 1 0 0 0 G 1 4 1 1 1 0 0 1 1 1 3 0 0 0 1 2 0 0 0 1 3 1 0 0 1 2 4 1 0 3 1 0 0 0 1 1 4 0 1 1 0 1 3 4 0 1 0 0 start pts , 2 directions. Each repeat 6 times. 6/6=1 3 hop cycles (1341) APTG 1 1 1 2 4 1 0 0 1 0 2 4 3 1 0 0 0 3 4 1 1 0 0 4 1 0 0 1 0 4 3 1 0 0 0 3 1 4 0 1 0 0 2 3 4 G 1 1341 CLG 1 1431 3413 3143 4134 4314 4 1 1 1 0 1 G 1 1 2 3 4 0 0 2 1 1 0 2 0 1 1 0 SPTG 1, init E 1=SP 1, 1 E 2=SP 2, 1 E 3=SP 3, 1 E 4=SP 4, 1 1 2 3 4 1 1 1 2 3 0 0 1 1 2 2 2 0 0 0 1 1 0 0 1 0 1 1 1 0 1 0 SPSFk 1 2 3 4 0 0 0 1 1 0 To extend to PT: k List. Eh PT 2 hk=Ek after zeroing the h bit of E k k List. PT 2 hj PT 3 hjk=Ek after zeroing E k j bit. k List. PT 3 hij PT 4 hijk=Ek after zeroing i and j bits of E k E 2 key 1, 1, 1, 2 1, 1, 3 1, 1, 4 1, 2, 1 1, 2, 2 1, 2, 3 1, 2, 4 1, 3, 1 1, 3, 2 1, 3, 3 1, 3, 4 1, 4, 1 1, 4, 2 1, 4, 3 1, 4, 4 2, 1, 1 2, 1, 2 2, 1, 3 2, 1, 4 2, 2, 1 2, 2, 2, 3 2, 2, 4 2, 3, 1 2, 3, 2 2, 3, 3 2, 3, 4 2, 4, 1 2, 4, 2 2, 4, 3 2, 4, 4 3, 1, 1 3, 1, 2 3, 1, 3 3, 1, 4 3, 2, 1 3, 2, 2 3, 2, 3 3, 2, 4 3, 3, 1 3, 3, 2 3, 3, 3, 4, 1 3, 4, 2 3, 4, 3 3, 4, 4 4, 1, 1 4, 1, 2 4, 1, 3 4, 1, 4 4, 2, 1 4, 2, 2 4, 2, 3 4, 2, 4 4, 3, 1 4, 3, 2 4, 3, 3 4, 3, 4 4, 4, 1 4, 4, 2 4, 4, 3 4, 4, 4 P 0 E 2 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 PTG 1 E 3 pred=(NPZ)|(PZ&Acyclic. Path. End) 1 0 0 1 1 E 1 lev, pred=NPZ key 1, 1 1, 2 1, 3 1, 4 2, 1 2, 2 2, 3 2, 4 3, 1 3, 2 3, 3 3, 4 4, 1 4, 2 4, 3 4, 4 EG 1 0 0 1 1 0 1 3 0 0 0 1 E 2 lev str=4 pred=NPZ 1 0 0 1 1 2 0 0 0 1 3 1 0 0 1 4 1 1 1 0 1 3 4 1 1 0 0 1 4 0 1 1 0 2 0 0 0 1 3 1 0 0 1 2 4 1 0 3 1 0 0 0 1 3 4 1 1 0 0 4 1 0 0 1 0 4 3 1 0 0 0 3 1 4 0 1 1 0 3 4 1 0 0 1 0 4 1 3 0 0 0 1 4 3 1 0 0 0 1 2 4 1 0 0 1 4 3 1 0 0 0 2 4 3 1 0 0 0 4 1 1 1 0 APTG 1 E 3 predicate = (NPZ&Not. Cycle. End)| 1 0 0 1 1 1 3 0 0 0 1 1 3 4 0 1 0 0 E PT SPT APT of graph as predicate Trees on E(Max. Path. Length). SP 1, 1 SP 2, 1 SP 3, 1 SP 4, 1 1 1 2 1 3 1 4 1 0 0 0 1 1 1 SP 1, 2 SP 2, 2 SPVertex=3, Len=2 1 2 2 2 3 2 0 1 0 1 0 1 4 0 1 1 0 2 0 0 0 1 3 1 0 0 1 2 4 1 0 3 1 0 0 0 1 2 4 1 0 0 1 0 2 4 3 1 0 0 0 3 4 1 1 0 0 4 1 1 1 0 (PZ&Acyclic. Path. End) 4 1 0 0 1 0 4 3 1 0 0 0 3 1 4 0 1 0 0 SP 1, 1|2 SP 2, 1|2 SP 3, 1|2 3 12 4 12 0 1 1 12 2 12 SP 4, 1|2 E 3 key 1 , 1, 1, 1 1 , 1, 1, 2 1 , 1, 1, 3 1 , 1, 1, 4 1 , 1, 2, 1 1 , 1, 2, 2 1 , 1, 2, 3 1 , 1, 2, 4 1 , 1, 3, 1 1 , 1, 3, 2 1 , 1, 3, 3 1 , 1, 3, 4 1 , 1, 4, 1 1 , 1, 4, 2 1 , 1, 4, 3 1 , 1, 4, 4 1 , 2, 1, 1 1 , 2, 1, 2 1 , 2, 1, 3 1 , 2, 1, 4 1 , 2, 2, 1 1 , 2, 2, 2 1 , 2, 2, 3 1 , 2, 2, 4 1 , 2, 3, 1 1 , 2, 3, 2 1 , 2, 3, 3 1 , 2, 3, 4 1 , 2, 4, 1 1 , 2, 4, 2 1 , 2, 4, 3 1 , 2, 4, 4 1 , 3, 1, 1 1 , 3, 1, 2 1 , 3, 1, 3 1 , 3, 1, 4 1 , 3, 2, 1 1 , 3, 2, 2 1 , 3, 2, 3 1 , 3, 2, 4 1 , 3, 3, 1 1 , 3, 3, 2 1 , 3, 3, 3 1 , 3, 3, 4 1 , 3, 4, 1 1 , 3, 4, 2 1 , 3, 4, 3 1 , 3, 4, 4 1 , 4, 1, 1 1 , 4, 1, 2 1 , 4, 1, 3 1 , 4, 1, 4 1 , 4, 2, 1 1 , 4, 2, 2 1 , 4, 2, 3 1 , 4, 2, 4 1 , 4, 3, 1 1 , 4, 3, 2 1 , 4, 3, 3 1 , 4, 3, 4 1 , 4, 4, 1 1 , 4, 4, 2 1 , 4, 4, 3 1 , 4, 4, 4 2 , 1, 1, 1 2 , 1, 1, 2 2 , 1, 1, 3 2 , 1, 1, 4 2 , 1, 2, 1 2 , 1, 2, 2 2 , 1, 2, 3 2 , 1, 2, 4 2 , 1, 3, 1 2 , 1, 3, 2 2 , 1, 3, 3 2 , 1, 3, 4 2 , 1, 4, 1 2 , 1, 4, 2 2 , 1, 4, 3 2 , 1, 4, 4 2 , 2, 1, 1 2 , 2, 1, 2 2 , 2, 1, 3 2 , 2, 1, 4 2 , 2, 2, 1 2 , 2, 2, 2 2 , 2, 2, 3 2 , 2, 2, 4 2 , 2, 3, 1 2 , 2, 3, 2 2 , 2, 3, 3 2 , 2, 3, 4 2 , 2, 4, 1 2 , 2, 4, 2 2 , 2, 4, 3 2 , 2, 4, 4 2 , 3, 1, 1 2 , 3, 1, 2 2 , 3, 1, 3 2 , 3, 1, 4 2 , 3, 2, 1 2 , 3, 2, 2 2 , 3, 2, 3 2 , 3, 2, 4 2 , 3, 3, 1 2 , 3, 3, 2 2 , 3, 3, 3 2 , 3, 3, 4 2 , 3, 4, 1 2 , 3, 4, 2 2 , 3, 4, 3 2 , 3, 4, 4 2 , 4, 1, 1 2 , 4, 1, 2 2 , 4, 1, 3 2 , 4, 1, 4 2 , 4, 2, 1 2 , 4, 2, 2 2 , 4, 2, 3 2 , 4, 2, 4 2 , 4, 3, 1 2 , 4, 3, 2 2 , 4, 3, 3 2 , 4, 3, 4 2 , 4, 4, 1 2 , 4, 4, 2 2 , 4, 4, 3 2 , 4, 4, 4 3 , 1, 1, 1 3 , 1, 1, 2 3 , 1, 1, 3 3 , 1, 1, 4 3 , 1, 2, 1 3 , 1, 2, 2 3 , 1, 2, 3 3 , 1, 2, 4 3 , 1, 3, 1 3 , 1, 3, 2 3 , 1, 3, 3 3 , 1, 3, 4 3 , 1, 4, 1 3 , 1, 4, 2 3 , 1, 4, 3 3 , 1, 4, 4 3 , 2, 1, 1 3 , 2, 1, 2 3 , 2, 1, 3 3 , 2, 1, 4 3 , 2, 2, 1 3 , 2, 2, 2 3 , 2, 2, 3 3 , 2, 2, 4 3 , 2, 3, 1 3 , 2, 3, 2 P 0 E 3 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0

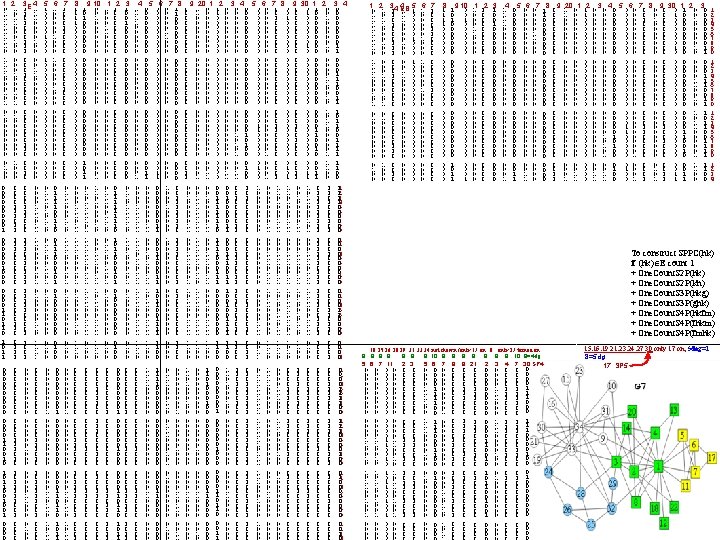
key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 SG Clique Mining PE 0 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 1 1 0 K=2: 2 Cliques (2 vertices): 12 13 14 16 23 24 34 56 67 Find endpts of each edges (Int((n-1)/7)+1, Mod(n-1, 7) +1) k=3: 123 124 134 234 k=4: 1234 (123 124 234 are cliques) 123, 134 1234. 123. 234 1234. 124, 134 1234. 124, 234 1234. 134, 234 1234 only 4 -clique Using the Edge. Count thm: on C={1, 2, 3, 4}, CU=C&EU C is a clique since ct(CU)=comb(4, 2)=4!/2!2!=6 have 124 CS 3 Have 123 CS 3 k=2: E=12 PE(2, 3)=1 So 123 CS 3 13 14 PE(2, 4)=1 124 CS 3 16 PE(1, 4)=1 134 CS 3 23 PE(2, 6)=0 PE(6, 7)=1 567 CS 3 24 Have 56 34 G 2 4 67. already have 567 PE(1, 5)=0 key 1, 1 1, 3 1, 4 1, 5 2 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 7 1, 2 1 PE(2, 3)=1 234 CS 3 57 6 5 PE(2, 4)=1 1234 CS 4 k=3: 123 PE(1, 7)=0 Have 1234 124 134 234 567 6 5 7 EC, requires counting 1’s in mask p. Tree of each Subgraph (or candidate Clique, if take the time to generate the CCSs – but then clearly the fastest way to finish up is simply to lookup the single bit position in E, i. e. , use EC). Edge. Count Algorithm (EC): |PUC| = (k+1)!/(k-1)!2! then C CCS The SG alg only needs Edge Mask p. Tree, E, and a fast way to find those pairs of subgraphs in CS k that share k-1 vertices (then check E to see if the two different kth vertices are an edge in G. Again this is a standard part of the Apriori ARM algorithm and has therefore been optimized and engineered ad infinitum!) G 3 1 2 4 3 k=2: 12 PE(2, 3)=1 123 CS 3 13 14 16 23 24 34 56 PE(4, 8)=1 248 CS 3 57 have PE(2, 6)=0 PE(2, 4)=1 124 CS 3 PE(2, 3)=1 234 CS 3 Have PE(1, 4)=1 134 CS 3 PE(1, 5)=0 67 18 PE(6, 7)=1 567 CS 3 PE(6, 8)=0 PE(1, 7)=0 PE(2, 8)=1 128 CS 3 PE(4, 8)=1 348 CS 3 28 k=4: 48. 1234 1238 1248 1348 2348 have PE(4, 8)=1 148 CS 3 k=5: PE(3, 8)=1 238 CS 3 PE(3, 8)=1 138 CS 3 EU 0 1 1 2 1 3 1 4 0 5 1 6 0 7 0 8 0 9 1 10 1 1 0 2 0 3 0 4 0 5 0 6 0 7 1 8 0 9 0 20 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 30 0 1 0 2 0 3 1 4 0 5 0 6 0 7 0 8 0 9 0 40 0 1 1 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 have PE(4, 8)=1 12348 CS 5 38 E 0 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 = 12348 CS 5. 6 PE(3, 8)=1 1238 CS 4 k=3: 123 PE(2, 4)=1 1234 CS 4 124 134 PE(4, 8)=1 1248 CS 4 PE(3, 8)=1 1348 CS 4 234 567 Have 5 G 4 128 138 148 238 248 348 7 1 2 4 3 PE(4, 8)=1 2348 CS 4 8 C 1 1 1 1 0 0 0 0 0 0 0 0 0 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 8 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 3, 8 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 4, 8 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 5, 8 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 6, 8 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 7, 8 8. 1 8, 2 8, 3 8, 4 8, 5 8, 6 8, 7 8. 8 CU 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 6 E 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0

The Edgep. Tree(E), Path. Tree(PT), Shortest. Pathv. Tree(SPT), 2 3 4 5 6 7 8 PTG 5 10 G 5 1 0 0 1 0 EG 5 2 -level str=8 1 0 0 1 0 2 1 0 0 0 0 3 0 0 0 1 4 0 1 0 0 0 5 1 0 0 0 1 0 6 0 0 1 7 1 0 0 0 1 0 8 0 0 1 2 0 0 0 1 0 0 0 1 3 6 0 0 0 0 1 3 6 8 0 0 1 0 0 0 1 5 0 0 0 1 0 1 7 0 0 1 0 0 0 2 1 0 0 1 0 1 5 7 1 0 0 0 0 1 7 5 1 0 0 0 0 2 1 5 0 0 0 1 0 2 1 7 0 0 1 0 0 0 0 1 0 3 8 0 0 0 1 0 0 4 2 1 0 0 0 0 5 1 0 0 0 0 1 0 3 8 6 0 0 1 0 0 0 4 2 1 0 0 1 0 5 1 2 0 0 0 1 0 0 4 2 1 5 0 0 0 1 0 APTG 5 2 1 0 0 0 0 3 0 0 0 1 1 2 0 0 0 1 0 0 2 1 0 0 1 0 3 6 0 0 0 0 1 1 0 0 1 0 1 5 0 0 0 1 0 1 7 0 0 1 0 0 0 2 1 5 0 0 0 1 0 2 1 7 0 0 1 0 0 0 3 8 0 0 0 1 0 0 4 0 1 0 0 0 5 1 0 0 0 1 0 4 2 1 0 0 0 0 5 1 0 0 0 0 1 0 4 2 1 0 0 1 0 5 1 2 0 0 0 1 0 0 4 2 1 5 0 0 0 1 0 4 2 1 7 0 0 1 0 0 0 6 0 0 1 5 7 1 0 0 0 0 6 3 0 0 0 0 1 7 1 0 0 0 6 8 0 0 1 0 0 0 7 5 1 0 0 0 0 7 1 2 0 0 0 1 0 0 7 5 1 0 0 0 0 7 5 1 2 0 0 0 1 0 0 5 1 7 0 0 0 0 1 0 0 0 5 7 1 0 0 0 0 6 3 0 0 0 0 1 6 8 0 0 1 0 0 0 7 1 0 0 0 5 7 1 0 0 0 6 3 8 0 0 0 1 0 0 6 8 3 0 0 0 1 0 0 7 1 2 0 0 0 1 0 0 7 1 5 0 0 0 1 0 4 2 1 7 0 0 1 0 0 0 8 3 0 0 0 1 8 3 7 4 6 7 5 1 0 0 0 0 8 3 0 0 0 1 0 0 8 6 0 0 1 0 0 0 7 5 1 0 0 0 0 1 0 8 3 6 0 0 0 0 1 8 6 3 0 0 0 0 1 2 5 7 5 1 2 0 0 0 1 0 0 8 0 0 1 0 0 7 1 0 0 0 0 1 Acyclic. Path. Tree(APT) and Cycle. List(CL) of a graph, 8 6 0 0 1 0 0 0 CLG 5 1571 1751 3683 3863 5175 5715 6386 6836 7157 7517 8368 8638 SPTG 5 1 2 3 4 5 6 77 8 0 1 0 0 2 1 0 0 0 0 0 2 1 0 0 1 2 0 0 3 0 0 0 11 0 2 00 03 0 0 1 0 1 0 2 0 0 0 1 0 3 0 0 0 1 11 00 00 00 0 1 0 0 PT Clique Miner Algorithm A clique is all cycles Extend to a k-plex (k-core) mining algorithm? PT(=APT+CL), SPT are powerful datamining tools with closure properties (to eliminate branches). Max clique Mining A k. Cycle is a k. Clique iff it’s found in CLk as PERM(k-1, k-1)/2=(k-1)!/2 k. Cycles (e. g. , vertices are repeated in CL for 3 cycles, 2!/2=1; 4 cycles, 3!/2=3; 5 cycles, 4!/2=12; 6 cycles, 5!/2=60. Downward closure: Once, a 4 cycle 12341 is established as a 4 clique (by the fact that {1, 2, 3, 4} occurs 3!/2=3 times in CL), all 3 vertex subsets are 3 cliques {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, so no need to check further. k-plex (missing k edges) mining alg? Density (internal edge density >> external|avg) mining alg? k-core (has k edges) mining alg? Degree (internal vertex degree >> external|avg) mining alg? Diameter. G 5 is max{Diameterk} = max{ 2, 2, 1, 3, 1}=3. Connected comp containing V 1, COMP 1={1, 2, 4, 5, 7}. Pick 1 st vertex not in COMP 1, 3, COMP 3 ={3, 6, 8}. Done. The partition is { {1, 2, 4, 5, 7}, {3, 6, 8} }. To pick the first vertex not in COMP 1, mask off COMP 1 with SPTv 1’ and then pick the first vertex in this complement.

1 1 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 2 0 0 0 1 0 0 0 1 2 0 0 0 1 0 0 0 0 0 1 22 10 00 00 00 00 1 22 00 00 00 10 00 00 00 1 2 0 0 1 0 0 0 1 3 1 0 0 0 0 1 3 0 0 1 0 0 0 0 1 3 0 0 0 1 0 0 0 0 0 3 0 0 0 0 0 0 1 1 4 0 1 1 0 0 0 5 0 0 0 1 1 0 0 0 0 0 1 1 44 10 00 00 00 00 55 10 00 00 00 00 1 1 4 0 0 0 1 0 0 0 0 0 5 0 0 0 1 0 0 0 0 1 1 4 0 0 0 1 0 0 0 0 0 5 0 0 1 0 0 0 0 1 4 0 0 0 0 5 0 1 0 0 0 0 1 6 1 0 0 0 0 0 1 6 0 0 0 1 0 0 0 0 1 6 0 0 1 0 0 0 0 0 0 0 6 0 0 0 0 1 7 0 0 1 1 0 0 0 0 0 1 7 0 1 0 0 0 0 1 7 0 0 0 1 0 0 0 0 1 77 00 00 00 01 00 00 00 1 7 0 1 0 0 0 0 1 8 0 0 0 1 0 0 0 0 0 0 1 8 0 1 0 0 0 0 0 1 8 0 0 0 1 0 0 0 1 8 0 0 1 0 0 0 1 9 0 0 0 1 0 0 1 99 00 00 00 10 10 00 00 0 9 0 0 0 0 0 0 0 0 0 9 0 0 0 0 1 a 0 0 0 1 0 0 1 a 0 0 0 0 1 0 0 0 0 0 0 0 a 0 0 0 0 0 0 0 0 1 b 0 0 0 1 0 0 1 b 0 0 0 0 0 1 0 0 0 0 0 0 0 b 0 0 0 0 0 0 0 0 1 c 0 0 0 0 1 1 1 0 0 0 0 0 0 c 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 d 0 0 0 0 1 1 0 d 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 e 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 e 0 0 0 0 1 f 0 0 0 1 0 0 1 0 f 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 SP 1 g 0 0 0 1 0 1 2 3 4 5 6 7 8 9 a b c d e f g 0 SP 2 g 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 0 SP 3 g 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 0 SP 4 g 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 0 SP 5 g 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g SP 1&2 1 0 0 1 1 1 0 0 0 0 0 2 0 0 1 1 0 0 0 3 1 1 0 1 0 0 0 0 0 SP 1&2&3 1 0 1 1 1 1 0 0 0 0 2 1 0 1 1 0 0 0 3 1 1 0 1 1 1 0 0 0 0 4 1 1 1 0 0 0 5 1 0 0 1 1 0 0 0 0 0 6 1 0 1 0 0 0 0 0 7 1 0 0 0 1 1 0 0 0 0 0 8 0 1 1 1 0 0 0 9 0 0 0 0 0 1 1 1 0 0 a 0 0 0 0 1 0 1 1 0 0 b 0 0 0 0 1 1 0 0 0 0 c 0 0 0 0 1 1 1 0 0 0 d 0 0 0 0 1 1 e 0 0 0 0 f 0 0 0 1 0 0 1 g 0 0 0 1 0 4 1 1 1 0 0 0 0 5 1 0 0 1 1 0 0 0 0 0 6 1 0 1 1 1 0 0 0 0 0 7 1 0 1 1 0 0 0 0 0 8 1 1 0 0 0 9 0 0 0 0 0 1 1 1 0 0 a 0 0 0 0 1 0 1 1 0 0 b 0 0 0 0 1 1 0 0 0 0 c 0 0 0 0 1 1 1 0 0 0 d 0 0 0 0 1 1 e 0 0 0 0 f 0 0 0 1 0 0 1 g 0 0 0 1 0 5 1 0 1 1 0 0 0 0 0 6 1 1 1 0 0 0 0 7 1 0 1 1 0 0 0 0 0 8 1 1 0 1 0 0 0 0 0 9 0 0 0 0 0 1 1 1 0 0 a 0 0 0 0 1 0 1 1 0 0 b 0 0 0 0 1 1 0 0 0 0 c 0 0 0 0 1 1 1 0 0 0 d 0 0 0 0 1 1 e 0 0 0 0 f 0 0 0 1 0 0 1 g 0 0 0 1 0 SP 1&2&3&4 1 0 1 1 1 1 0 0 0 0 2 1 0 1 0 1 0 0 0 0 3 1 1 0 1 1 1 0 0 0 0 7 7 7 1 0 1 1 1 1 0 0 0 0 2 1 0 1 1 1 0 0 0 0 3 1 1 0 1 1 1 0 0 0 0 4 1 1 1 0 0 0 0 5 1 1 0 1 1 1 0 0 0 0 6 1 1 1 0 0 0 0 7 1 1 1 0 1 0 0 0 0 8 1 1 1 1 0 0 0 0 0 9 0 0 0 0 0 1 1 1 0 0 a 0 0 0 0 1 0 1 1 0 0 b 0 0 0 0 1 1 0 0 0 0 0 0 0 0 2 0 0 0 0 3 0 0 0 0 4 1 1 1 0 0 0 0 4 0 0 0 0 5 0 0 0 0 7 6 0 0 0 0 7 7 0 0 0 0 7 8 0 0 0 0 3 9 0 0 0 0 3 a 0 0 0 0 3 b 0 0 0 0 3 2 c 0 0 0 0 1 1 1 0 0 0 d 0 0 0 0 1 1 0 0 c 0 0 0 0 d 0 0 0 0 0 2 e 0 0 0 0 0 e 0 0 0 0 A 2 Ps 1 2 3 4 5 6 7 8 9 a b c d e f g A 3 Ps 1 2 3 4 5 6 7 8 9 a b c d e f g 1 3 0 0 0 1 0 0 0 1 6 0 0 1 0 0 0 0 0 1 3 4 0 1 0 0 0 1 6 5 0 0 0 1 0 0 0 0 0 2 4 0 0 1 0 0 0 0 0 3 1 0 0 0 0 1 6 7 0 0 1 0 0 0 g 0 0 0 1 0 0 0 SP 6 g 0 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 2 4 3 1 0 0 0 0 3 1 6 5 0 0 0 1 0 0 0 0 0 3 1 6 7 0 0 1 0 0 0 4 3 1 6 0 0 1 0 0 0 0 0 5 6 1 3 0 0 0 1 0 0 0 5 7 6 1 0 0 0 0 3 1 0 0 0 0 3 4 0 1 0 0 0 2 4 3 1 0 0 0 0 3 1 6 0 0 1 0 0 0 0 0 6 1 3 4 0 1 0 0 0 7 5 6 1 0 0 0 0 2 SP 1&2&3&4&5 COMPLETE f 0 0 0 1 0 0 1 f 0 0 0 0 2 0 0 0 1 0 0 0 1 0 0 0 0 0 4 0 1 1 0 0 0 0 0 0 4 3 1 0 0 0 0 0 5 0 0 0 1 1 0 0 0 0 0 5 6 1 0 0 0 0 0 6 1 0 0 0 0 0 7 0 0 1 1 0 0 0 0 0 8 0 0 0 1 0 0 0 6 1 0 0 0 0 6 5 0 0 0 1 0 0 0 0 0 6 7 0 0 1 0 0 0 7 5 0 0 0 1 0 0 0 0 0 7 6 1 0 0 0 0 8 4 0 1 1 0 0 0 0 9 c 0 0 0 0 0 1 1 0 0 0 A c 0 0 0 0 1 0 0 0 b c 0 0 0 0 1 1 0 0 0 5 7 6 0 0 1 0 0 0 5 7 6 1 0 0 0 0 6 1 3 0 0 0 1 0 0 0 6 5 7 0 0 0 1 0 0 0 0 0 6 7 5 0 0 0 1 0 0 0 0 0 7 5 6 1 0 0 0 0 0 0 0 0 7 6 5 0 0 0 1 0 0 0 0 0 5 7 0 0 0 1 0 0 0 0 0 5 6 7 0 0 1 0 0 0 8 4 3 1 0 0 0 0 b 0 0 0 1 0 0 a 0 0 0 1 0 0 d 0 0 0 0 1 1 c 0 0 0 0 1 1 1 0 0 0 e 0 0 0 0 f 0 0 0 1 0 0 1 g 0 0 0 1 0 D g 0 0 0 0 1 0 F d 0 0 0 0 1 1 2 3 4 5 6 7 8 9 a b c d e f g 2 4 3 1 6 0 0 1 0 0 0 0 0 E=A 1 Ps 1 2 3 4 5 6 7 8 9 a b c d e f g cycles in blue (not in APT) D f 0 0 0 0 1 8 4 3 1 0 0 0 0 D F g 0 0 0 1 0 0 0 D G f 0 0 0 1 0 0 0 1 2 3 4 5 6 7 8 9 a b c d e f g 2 4 3 1 6 5 0 0 0 1 0 0 0 0 0 2 4 3 1 6 7 0 0 1 0 0 0 A 5 Ps A 4 Ps 7 6 1 3 0 0 0 1 0 0 0 9 0 0 0 1 0 0 4 3 1 6 5 0 0 0 1 0 0 0 0 0 4 3 1 6 7 0 0 1 0 0 0 5 6 1 3 4 0 1 0 0 0 5 7 6 1 3 0 0 0 1 0 0 0 7 5 6 1 3 0 0 0 1 0 0 0 7 6 1 3 4 0 1 0 0 0 8 4 3 1 6 0 0 1 0 0 0 0 0 6 5 1 4 G 6 F g 0 0 0 1 0 0 0 F D g 0 0 0 0 1 0 G f 0 0 0 1 0 0 0 G d 0 0 0 0 1 0 F G d 0 0 0 0 1 0 A 6 Ps 5 7 6 1 3 4 0 1 0 0 0 7 5 6 1 3 4 0 1 0 0 0 G D f 0 0 0 0 1 G F d 0 0 0 0 1 8 4 3 1 6 5 0 0 0 1 0 0 0 0 0 8 4 3 1 6 7 0 0 1 0 0 0 9 a b c d e f g 7 2 3

All Shortest Path p. Trees for a unipartite undirected graph, G 7 (SP 1, SP 2, SP 3, SP 4, SP 5) 9 13 19 16 13 12 13 17 24 19 14 25 15 15 3 15 16 26 15 16 16 15 6 6 13 20 21 15 20 26 11 6=2 dg 16 9 10 6 3 4 4 4 5 2 3 1 2 5 2 2 2 3 2 2 2 5 3 3 2 4 3 4 4 6 11 16=1 deg 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 20 1 2 3 4 5 6 7 8 9 30 1 2 3 0 0 0 1 0 0 0 0 1 1 0 1 1 SP 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 04 SP 2 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 8 11 4 11 8 8 8 12 3 11 8 8 9 3 6 6 12 8 6 4 6 8 6 4 23 23 6 7 8 5 8 1 10 10=3 dg 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 20 1 2 3 4 5 6 7 8 9 30 1 2 3 4 0 0 0 SP 3 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 0 0 02 03 04 15 16 17 18 09 00 11 12 13 04 05 06 07 18 09 00 01 12 03 04 05 06 07 08 09 00 01 02 13 04 2 3 4 5 6 7 8 9 0 1 2 3 4 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1 0 1 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 0 1 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 1 1 0 0 10, 25, 26, 28, 29, 33, 34 not shown (only 17 on, 1=4 dg) 8 8 8 9 10 8 8 8 8 10 8=4 dg 5 6 7 11 2 3 5 6 7 8 9 21 2 3 4 7 30 SP 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 1 1 0 1 0 1 0 1 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 1 0 0 0 1 1 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 1 1 1 1 0 1 0 0 0 0 0 1 1 1 0 0 1 1 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 15, 16, 19, 21, 23, 24, 27, 30 only 17 on, 5 deg=1 8=5 dg 17 SP 5

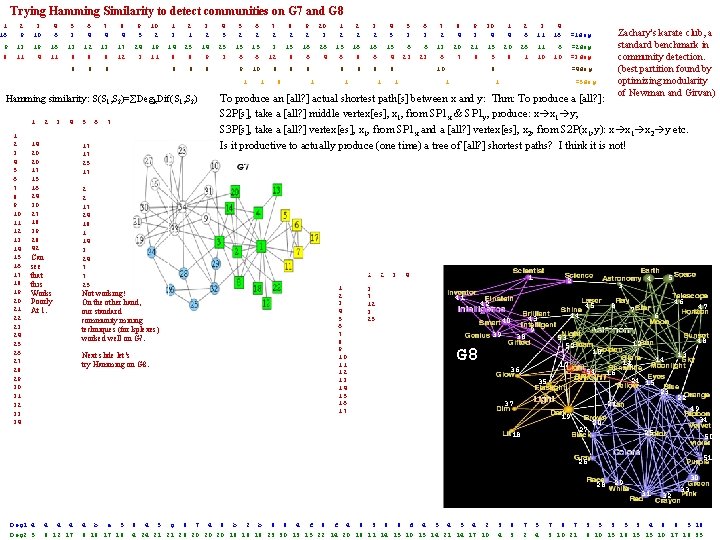
Trying Hamming Similarity to detect communities on G 7 and G 8 1 16 2 9 3 10 4 6 5 3 6 4 7 4 9 13 8 11 8 4 9 5 19 16 13 12 4 11 8 8 8 10 2 1 3 2 4 5 5 2 6 2 13 17 8 12 24 19 14 25 15 3 11 8 8 9 3 6 8 8 8 9 1 Hamming similarity: S(S 1, S 2)= Degk. Dif(S 1, S 2) 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 2 3 4 14 20 20 17 15 16 24 30 27 18 39 28 42 5 6 7 17 17 25 17 Can see that this Works Poorly At 1. 2 2 17 24 18 1 14 3 24 7 7 25 7 2 8 2 9 2 20 3 1 2 2 2 3 2 4 5 15 3 15 16 26 15 16 16 15 6 12 8 6 4 6 8 6 4 8 8 10 1 8 8 1 Next slide let’s try Hamming on G 8. 6 3 7 2 8 4 9 3 30 4 1 4 2 6 6 6 13 20 21 15 20 26 11 6 =2 deg 23 23 6 7 8 5 8 1 10 10 =3 deg 8 1 10 1 3 11 4 16 8 1 Zachary's karate club, a standard benchmark in community detection. (best partition found by optimizing modularity of Newman and Girvan) =1 deg =4 deg 1 =5 deg To produce an [all? ] actual shortest path[s] between x and y: Thm: To produce a [all? ]: S 2 P[s], take a [all? ] middle vertex[es], x 1, from SP 1 x & SP 1 y, produce: x x 1 y; S 3 P[s], take a [all? ] vertex[es], x 1, from SP 1 x and a [all? ] vertex[es], x 2, from S 2 P(x 1, y): x x 1 x 2 y etc. Is it productive to actually produce (one time) a tree of [all? ] shortest paths? I think it is not! 1 Not working! On the other hand, our standard community mining techniques (for kplexes) worked well on G 7. 5 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 3 7 12 3 25 2 3 4 1 41 2 42 8 45 40 39 G 8 38 53 52 17 36 46 7 44 43 9 48 14 11 16 35 37 24 15 23 21 19 27 18 47 6 12 10 54 5 4 3 13 22 49 34 20 25 50 51 26 28 Deg 1 4 Deg 2 5 4 4 4 8 12 17 4 b a 5 8 16 17 16 6 4 5 g 9 7 4 6 b 2 b 8 6 4 f 9 f 4 9 3 8 6 d 4 5 4 24 21 21 26 20 20 20 19 16 19 23 30 13 15 22 14 20 18 11 14 15 10 15 14 21 14 17 10 3 4 6 3 7 2 5 4 7 6 7 3 10 21 30 29 31 32 33 3 5 3 4 9 6 5 19 8 10 15 18 15 15 10 17 18 35

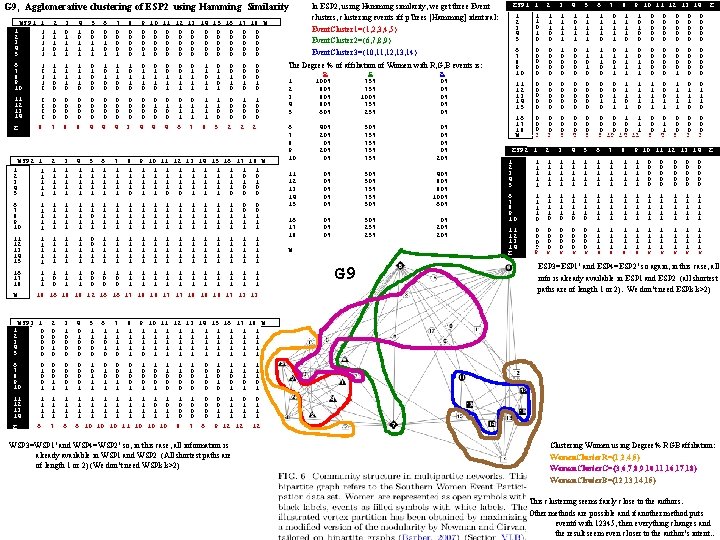
G 9, Agglomerative clustering of ESP 2 using Hamming Similarity 1 2 3 4 5 WSP 1 1 1 1 6 7 8 9 10 11 12 13 14 E 1 0 1 1 0 2 1 1 1 0 1 3 0 1 1 4 1 0 1 1 1 5 0 0 1 1 1 6 0 0 1 7 0 0 1 8 0 0 0 9 10 11 12 13 14 15 16 17 18 W 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 1 0 0 1 0 1 0 0 1 1 0 0 1 1 1 0 0 0 0 0 8 4 4 4 0 0 3 0 0 1 1 0 0 0 4 4 4 0 0 0 8 7 8 0 1 1 1 0 1 1 0 0 1 1 1 6 7 1 1 0 0 1 1 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 0 0 8 5 2 2 2 WSP 2 1 1 1 2 1 3 1 4 1 5 1 2 1 1 1 3 1 1 1 4 5 1 1 1 1 1 6 1 1 1 7 1 1 1 8 1 1 0 9 10 11 12 13 14 15 16 17 18 W 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0 0 0 6 7 8 9 10 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 11 12 13 14 15 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 16 17 18 W 1 1 0 1 1 1 1 0 1 1 0 0 0 1 1 1 1 1 18 16 18 18 12 16 16 17 18 18 17 17 18 18 18 17 13 13 WSP 3 1 2 3 4 5 1 2 0 0 0 0 1 0 0 3 1 0 0 4 0 1 0 0 0 5 6 7 1 1 1 0 0 0 8 1 1 1 9 10 11 12 13 14 15 16 17 18 W 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 6 7 8 9 10 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1 6 7 1 1 6 11 12 13 14 E 0 1 1 0 0 0 1 0 0 0 1 0 1 1 0 1 In ESP 2, using Hamming similarity, we get three Event clusters, clustering events iff p. Trees [Hamming] identical: Event. Cluster 1={1, 2, 3, 4, 5} Event. Cluster 2={6, 7, 8, 9} Event. Cluster 3={10, 11, 12, 13, 14} ESP 1 1 2 3 4 5 6 1 2 3 4 5 1 1 0 1 1 1 0 0 1 1 1 1 1 0 0 1 1 1 1 0 1 0 0 0 0 0 0 0 6 7 8 9 10 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 0 0 0 0 11 12 13 14 15 0 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 0 16 17 18 W 0 0 0 3 0 0 0 6 0 0 0 4 0 0 0 8 0 0 1 1 0 0 0 1 8 10 14 12 0 0 0 1 0 0 5 4 6 3 0 0 0 3 2 3 4 5 6 7 8 9 10 11 12 13 14 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 The Degree % of affiliation of Women with R, G, B events is: R 100% 80% 80% 60% G 75% 100% 75% 25% B 0% 0% 0% 6 7 8 9 10 40% 20% 0% 50% 75% 75% 0% 0% 20% 11 12 13 14 15 0% 0% 0% 50% 75% 50% 40% 80% 100% 60% 16 17 18 0% 0% 0% 50% 25% 0% 20% 1 2 3 4 5 W G 9 ESP 2 1 7 8 9 10 11 12 13 14 1 2 3 4 5 1 1 1 1 1 6 7 8 9 10 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 11 12 13 14 E 0 0 0 0 9 9 0 0 0 0 9 1 1 1 1 e 1 1 1 1 9 1 1 9 E E ESP 3=ESP 1’ and ESP 4=ESP 2’ so again, in this case, all info is already available in ESP 1 and ESP 2 (all shortest paths are of length 1 or 2). We don’t need ESPk k>2) 1 1 1 0 1 1 1 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 1 6 10 10 10 11 10 10 10 8 7 6 9 12 12 12 WSP 3=WSP 1’ and WSP 4=WSP 2’ so, in this case, all information is already available in WSP 1 and WSP 2 (All shortest paths are of length 1 or 2) (We don’t need WSPk k>2) Clustering Women using Degree% RGB affiliation: Women. Cluster. R={1, 2, 4, 5} Woman. Cluster. G={3, 6, 7, 8, 9, 10, 11, 16, 17, 18} Woman. Clsuter. B={12, 13, 14, 15} This clustering seems fairly close to the authors. Other methods are possible and if another method puts event 6 with 12345, then everything changes and the result seem even closer to the author’s intent. .

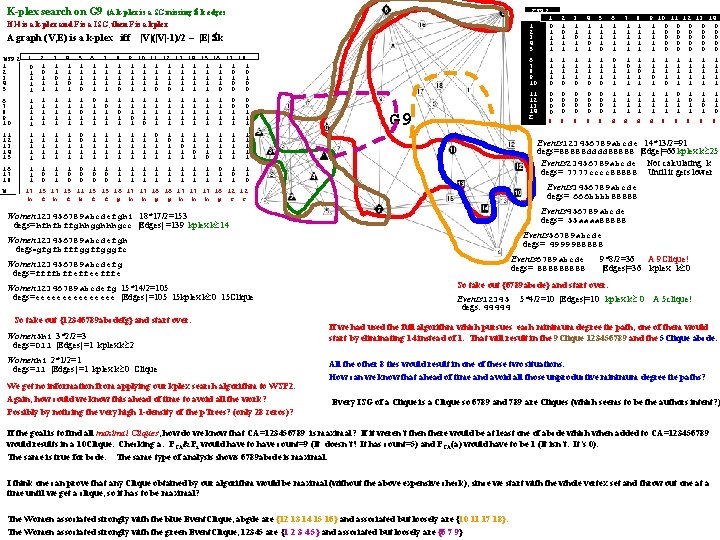
K-plex search on G 9 (A k-plex is a SG missing k edges If H is a k-plex and F is a ISG, then F is a kplex A graph (V, E) is a k-plex iff |V|(|V|-1)/2 – |E| k WSP 2 1 2 3 4 5 1 2 0 1 1 1 1 3 1 1 0 1 1 4 5 1 1 1 0 6 1 1 1 7 1 1 1 8 1 1 0 9 10 11 12 13 14 15 16 17 18 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0 0 0 6 7 8 9 10 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 11 12 13 14 15 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 16 17 18 W G 9 We get no information from applying our kplex search algorithm to WSP 2. Again, how could we know this ahead of time to avoid all the work? Possibly by noticing the very high 1 -density of the p. Trees? (only 28 zeros)? 5 1 1 0 6 1 1 1 6 7 8 9 10 1 1 1 1 0 1 1 0 0 1 1 11 12 13 14 E 0 0 0 0 8 8 0 0 0 0 8 1 1 d 7 8 1 1 1 0 1 1 1 0 1 1 9 10 11 12 13 14 1 0 0 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 d d d 8 8 8 Events 56789 abcde 14*13/2=91 degs= 4999988888 |Edges|=66 kplex k 25 Events 6789 abcde degs= 88888 Women 123456789 abcdefg 18*17/2=153 degs=ffffbffeffeefffe |Edges| =139 kplex k 14 Womenhi 2*1/2=1 degs=11 |Edges| =1 kplex k 0 Clique 4 1 1 1 0 1 Events 456789 abcde 14*13/2=91 degs= 55 aaaa 88888 |Edges|=66 kplex k 25 Women 123456789 abcdefgh 18*17/2=153 degs=gfgfbfffgggfc |Edges| =139 kplex k 14 Women 5 hi 3*2/2=3 degs=011 |Edges| =1 kplex k 2 3 1 1 0 1 1 Events 3456789 abcde 14*13/2=91 degs= 666 bbbb 88888 |Edges|=66 kpl Women 123456789 abcdefghi 18*17/2=153 degs=hfhfbffghhgghhhgcc |Edges| =139 kplex k 14 So take out {12346789 abcdefg} and start over. 2 1 0 1 1 1 Events 123456789 abcde 14*13/2=91 degs=88888 dddd 88888 |Edge|=66 kplex k 25 Events 23456789 abcde Not calculating k degs= 7777 cccc 88888 Until it gets lower 1 1 0 1 1 1 0 0 0 0 1 1 1 1 1 0 17 15 11 15 15 16 17 17 16 16 17 17 17 16 12 12 h f b f f g h h g g h h h g c c Women 12346789 abcdefg 15*14/2=105 degs=eeeeeeee |Edges| =105 15 kplex k 0 15 Clique ESP 2 1 1 0 2 1 3 1 4 1 5 1 9*8/2=36 A 9 Clique! |Edges|=36 kplex k 0 So take out {6789 abcde} and start over. Events 12345 degs: 44444 5*4/2=10 |Edges|=10 kplex k 0 A 5 clique! If we had used the full algorithm which pursues each minimum degree tie path, one of them would start by eliminating 14 instead of 1. That will result in the 9 Clique 123456789 and the 5 Clique abcde. All the other 8 ties would result in one of these two situations. How can we know that ahead of time and avoid all those unproductive minimum degree tie paths? Every ISG of a Clique is a Clique so 6789 and 789 are Cliques (which seems to be the authors intent? ) If the goal is to find all maximal Cliques, how do we know that CA=123456789 is maximal? If it weren’t then there would be at least one of abcde which when added to CA=123456789 would results in a 10 Clique. Checking a: PCA&Pa would have to have count=9 (It doesn’t! It has count=5) and PCA(a) would have to be 1 (It isn’t. It’s 0). The same is true for bcde. The same type of analysis shows 6789 abcde is maximal. I think one can prove that any Clique obtained by our algorithm would be maximal (without the above expensive check), since we start with the whole vertex set and throw out one at a time until we get a clique, so it has to be maximal? The Women associated strongly with the blue Event. Clique, abgde are {12 13 14 15 16} and associated but loosely are {10 11 17 18}. The Women associated strongly with the green Event. Clique, 12345 are {1 2 3 4 5} and associated but loosely are {6 7 9}

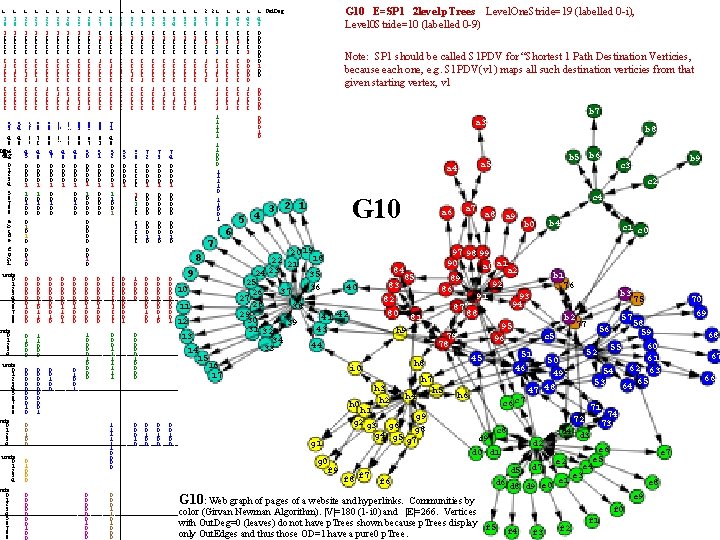
1 1 1 1 1 2 21 1 1 Out. Deg 1 8 1 0 0 0 0 1 9 1 0 0 0 0 2 0 1 0 0 0 2 1 1 0 0 0 0 1 0 0 0 2 2 1 0 0 0 0 0 1 0 0 2 3 1 0 0 0 0 0 1 0 0 0 2 4 1 0 0 0 1 0 0 2 5 1 0 0 0 1 0 2 6 1 0 0 0 0 1 2 7 0 1 0 0 0 2 8 0 1 0 0 0 2 9 0 1 0 0 0 0 3 0 0 1 0 0 0 3 1 0 0 0 0 1 0 0 0 3 2 0 1 0 0 0 0 1 0 0 3 3 0 1 0 0 0 0 0 1 0 0 0 3 5 0 1 0 0 0 1 0 3 6 0 1 0 0 0 1 3 7 0 0 1 0 3 9 0 0 1 0 0 0 1 4 0 0 0 1 0 0 4 2 0 0 0 0 1 0 0 0 0 4 3 0 0 0 0 1 0 0 5 7 6 9 4 5 0 0 1 1 0 1 0 0 0 1 0 5 8 7 0 4 6 0 0 1 1 0 0 5 9 6 8 4 7 0 0 1 0 0 6 6 0 1 6 6 7 6 4 8 0 0 1 6 3 6 6 4 9 0 0 1 0 0 6 5 e 7 5 0 0 0 1 1 0 0 0 1 0 6 6 6 1 5 1 0 0 0 0 0 7 1 4 9 5 2 0 0 1 1 1 0 0 0 0 1 0 1 1 0 0 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 5 3 4 8 tens dig 0 1 2 3 4 5 6 7 8 9 a b c d e f g h i units 0 1 2 3 4 5 6 7 8 9 units 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 0 5 6 0 0 0 1 0 0 0 7 2 0 0 1 0 0 0 0 1 0 7 3 0 0 1 0 0 0 0 1 0 7 4 0 0 1 0 0 0 0 1 0 7 0 0 0 1 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 9 10 11 12 13 14 15 16 17 G 10 E=SP 1 2 level p. Trees Level. One. Stride=19 (labelled 0 -i), Level 0 Stride=10 (labelled 0 -9) Note: SP 1 should be called S 1 PDV for “Shortest 1 Path Destination Verticies, because each one, e. g. S 1 PDV(v 1) maps all such destination verticies from that given starting vertex, v 1 0 0 0 0 1 0 b 7 a 3 0 0 0 1 1 0 0 0 0 1 0 0 b 8 b 6 b 5 a 4 b 9 c 3 c 2 6 8 1 1 1 0 0 0 0 0 1 0 0 5 5 0 0 1 3 8 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 0 1 5 4 c 4 G 10 3 2 1 20 19 18 22 21 23 24 35 25 36 40 37 26 27 28 38 29 41 42 30 39 43 31 32 34 44 33 g 1 g 0 f 9 a 6 84 85 83 82 80 81 h 9 h 8 i 0 h 0 0 0 1 2 3 4 units 5 4 4 8 3 4 0 1 0 0 0 0 0 1 0 0 h 3 h 2 h 4 a 8 a 9 46 h 6 c 7 c 9 G 10: Web graph of pages of a website and hyperlinks. c 1 c 0 b 1 76 b 2 b 3 58 59 60 55 52 61 62 63 54 65 53 64 50 49 48 47 56 71 d 4 d 2 d 7 e 2 d 6 d 8 d 9 e 0 e 1 Communities by color (Girvan Newman Algorithm). |V|=180 (1 -i 0) and |E|=266. Vertices with Out. Deg=0 (leaves) do not have p. Trees shown because p. Trees display f 5 only Out. Edges and thus those OD=1 have a pure 0 p. Tree. 74 73 d 3 e 6 e 5 e 4 e 3 e 7 e 8 e 9 f 0 f 4 75 57 77 c 5 c 8 d 5 f 6 b 4 72 d 0 d 1 f 8 f 7 b 0 97 98 99 90 a 1 a 2 89 92 86 93 91 94 87 88 95 79 96 78 51 45 h 7 h 5 h 1 g 9 g 2 g 3 g 6 g 8 g 4 g 5 g 7 a 7 f 3 f 2 f 1 70 69 68 67 66

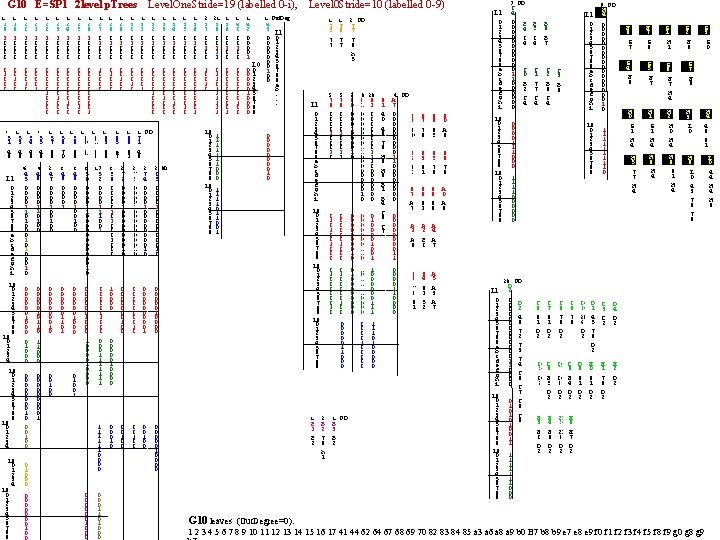
G 10 E=SP 1 2 level p. Trees Level. One. Stride=19 (labelled 0 -i), 1 1 1 8 1 0 0 1 1 9 1 0 0 0 2 0 1 0 0 1 5 3 4 8 1 5 4 4 8 L 0 L 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 1 2 2 1 0 0 0 0 1 6 L 1 0 1 2 3 4 5 6 7 8 9 a b c d e f g h i 1 2 1 1 0 0 0 0 1 5 1 4 6 1 0 0 0 1 5 5 4 9 6 4 5 0 0 1 1 0 1 0 0 0 1 0 4 6 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 5 7 6 9 2 4 7 0 0 1 0 0 0 1 0 1 1 2 4 1 0 0 2 5 1 0 0 2 6 1 0 0 2 7 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 5 8 7 0 3 4 8 0 0 1 0 0 0 1 1 5 9 6 8 3 4 9 0 0 1 0 0 0 0 0 1 0 0 1 1 6 0 6 7 3 5 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 0 1 6 6 1 2 8 0 1 0 0 0 1 17 5 2 0 0 1 1 1 0 0 1 1 5 6 0 0 0 1 1 1 3 0 0 1 0 0 0 3 2 0 1 0 0 0 3 3 0 1 0 0 0 3 4 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 6 6 6 1 2 7 2 0 0 1 0 0 0 0 1 0 7 1 4 9 2 7 3 0 0 1 0 0 0 0 1 0 2 7 4 0 0 1 0 0 0 0 1 0 1 3 5 0 1 0 0 0 1 3 6 0 1 0 0 0 1 2 21 1 3 7 0 0 1 0 0 3 8 0 0 1 1 0 1 1 1 L 0 1 OD 1 6 5 e 7 3 1 2 9 0 1 0 0 0 1 6 3 6 6 1 2 OD C 5 0 0 1 0 0 1 2 3 4 5 6 7 8 9 1 1 1 1 0 0 1 2 3 4 5 6 7 8 9 1 1 0 0 1 L 0 3 9 0 0 1 4 0 0 0 1 4 2 0 0 1 1 Out. Deg 4 3 0 0 0 L 0 0 00 1 0 0 0 02 0 03 0 0 04 0 0 15 0 0 06 0 1 07 0 0 08 1 0 09 L 1 0 1 2 3 4 5 6 7 8 9 a b. . . 0 0 0 0 1 0 1 7 5 7 8 0 0 1 0 L 1 0 1 2 3 4 5 6 7 8 9 a b c d e f g h i L 0 0 1 2 3 4 5 6 7 8 9 L 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1 2 3 4 5 6 7 8 9 0 0 0 1 0 0 7 6 7 7 5 7 9 0 0 1 0 0 0 1 1 2 OD 7 7 7 6 h 5 2 8 0 0 0 0 1 0 8 20 8 1 0 0 0 0 1 0 9 1 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 L 0 0 0 1 1 0 0 1 2 3 4 5 6 7 8 9 0 0 0 1 9 1 4 0 4 6 7 6 H 8 H 9 B 1 B 4 C 6 C 7 4 OD A 7 0 0 0 0 0 1 1 0 0 0 0 8 6 8 0 8 7 7 9 8 5 9 0 A 6 9 2 9 1 9 3 9 1 9 5 7 9 9 6 7 8 9 7 A 7 9 8 9 1 9 9 8 8 A 0 A 8 A 1 A 9 A 2 B 0 A 4 A 7 8 8 7 8 9 1 9 4 9 1 5 2 A 5 A 3 A 7 7 OD L 1 0 1 2 3 4 5 6 7 8 9 a b c d e f g h i L 0 0 1 2 3 4 5 6 7 8 9 1 1 1 1 0 0 0 0 0 1 1 0 0 0 0 1 0 0 B 1 B 2 0 0 0 1 0 0 2 B 2 7 6 h 1 1 OD B 3 B 2 C 4 0 0 0 1 1 0 0 0 9 OD B 4 C 4 B 5 C 4 C 0 B 2 C 4 C 1 7 7 C 4 L 1 0 1 2 3 4 5 6 7 8 9 a b c d e f g h i B 6 B 7 C 2 B 9 C 4 C 3 B 8 0 0 1 1 1 0 0 0 L 0 1 1 0 0 0 H 4 0 0 0 0 0 1 0 F 6 G 7 F 7 G 6 G 1 H 1 G 4 F 8 G 5 F 7 G 6 F 7 H 4 G 7 F 6 H 1 G 1 H 4 H 2 H 0 H 4 H 3 I 0 H 6 H 4 H 8 9 1 H 4 H 0 G 1 H 4 0 1 2 3 4 5 6 7 8 9 1 1 1 1 1 0 D 1 4 5 7 8 D 2 D 3 D 2 D 4 D 2 E 0 9 1 D 2 E 1 7 9 D 2 E 2 D 2 H 5 7 7 H 4 G 2 F 9 G 3 G 0 H 4 4 6 8 1 H 9 I 0 4 3 7 8 7 9 20 OD L 1 0 1 2 3 4 5 6 7 8 9 a b c d e f g h i L 0 0 1 0 0 0 0 0 1 2 3 1 0 0 1 1 0 0 0 1 Level 0 Stride=10 (labelled 0 -9) 0 1 2 3 4 5 6 7 8 9 L 0 0 1 2 3 4 5 6 7 8 9 D 2 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 1 1 1 0 0 0 D 2 4 6 7 2 7 3 7 4 C 6 C 7 C 8 C 9 C 6 9 1 D 2 C 7 9 1 D 2 C 8 7 9 D 2 C 9 7 8 D 5 D 2 D 6 F 5 D 2 D 7 D 9 D 2 D 8 F 4 D 2 E 3 F 0 D 2 E 4 E 9 D 2 E 5 E 8 D 2 E 6 E 7 D 2 D 0 H 4 D 2 D 9 9 1 D 2 G 10 leaves (Out. Degree=0): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 41 44 62 64 67 68 69 70 82 83 84 85 a 3 a 6 a 8 a 9 b 0 B 7 b 8 b 9 e 7 e 8 e 9 f 0 f 1 f 2 f 3 f 4 f 5 f 8 f 9 g 0 g 8 g 9 I 0 4 4 H 9

18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 42 43 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 27 32 40 46 29 27 45 78 G 10 E=SP 1 Lists 75 76 77 78 77 77 76 H 5 41 43 46 81 88 79 46 81 87 95 96 80 38 81 81 78 79 83 84 85 86 80 24 29 34 42 25 30 35 43 26 31 36 45 D 4 D 2 D 5 D 2 D 6 E 5 D 2 7 12 17 50 B 2 8 13 18 51 D 1 9 14 19 71 H 7 51 78 B 2 D 1 43 41 46 81 88 E 0 91 D 2 45 41 43 45 47 48 50 76 D 2 H 1 81 88 76 97 A 2 C 7 81 98 A 4 H 8 86 99 B 1 H 9 E 1 79 D 2 E 2 D 2 46 46 49 55 72 78 B 2 D 1 H 6 H 7 E 3 F 0 D 2 E 4 E 9 D 2 93 91 47 46 49 D 2 48 45 48 50 51 72 74 E 5 E 8 D 2 94 91 52 E 6 E 7 D 2 95 79 49 45 47 48 49 50 51 D 2 F 6 G 7 F 7 G 6 G 1 H 1 G 2 F 9 G 3 G 0 G 4 F 8 G 5 F 7 53 46 47 49 G 6 F 7 H 4 54 46 47 49 G 7 F 6 55 46 71 74 H 0 G 1 H 4 B 1 B 2 H 1 G 1 H 4 56 46 51 55 77 B 2 H 6 B 2 76 H 1 B 3 B 2 H 0 H 4 H 3 I 0 B 4 C 4 H 4 46 81 H 0 H 1 H 2 H 3 H 5 H 6 H 7 H 8 96 78 97 A 7 98 91 99 88 A 1 A 9 A 4 A 7 A 5 A 3 A 7 98 99 A 4 A 5 50 45 47 48 49 50 H 4 51 45 47 48 50 52 45 47 48 49 50 51 66 67 68 69 70 75 B 3 63 1 49 46 74 B 5 C 4 55 49 B 6 B 7 H 5 77 H 4 56 50 75 B 3 C 0 B 2 C 4 H 6 H 4 57 69 C 1 77 C 4 H 8 91 H 4 58 70 C 2 B 9 C 4 H 9 I 0 43 78 79 59 68 C 3 B 8 I 0 44 H 9 60 67 C 4 B 5 B 6 C 0 C 1 C 2 C 3 c 5 45 D 5 65 E 7 C 6 91 D 2 66 61 71 49 C 7 91 D 2 72 47 D 2 C 9 78 73 48 D 2 D 0 H 4 D 2 74 49 D 2 6 5 11 16 48 78 90 A 6 91 40 46 89 90 A 1 B 4 C 6 92 91 54 48 63 66 SP 2 Lists 36 2 37 3 38 4 10 15 47 74 39 12 40 10 42 46 H 7 D 9 91 D 2 A 2 B 0 61 66 C 6 D 3 E 1 E 6 89 85 47 48 72 48 46 47 49 51 46 52 46 53 54 55 56 57 58 59 60 61 62 63 64 53 48 74 D 1 E 0 E 5 D 8 E 4 D 2 A 0 A 8 50 46 51 55 H 6 73 C 9 D 9 E 4 88 78 91 45 46 51 78 B 2 D 1 H 7 46 45 47 48 50 51 49 46 71 74 72 C 8 D 8 E 3 D 7 D 9 D 2 87 79 23 22 28 33 41 49 D 2 46 C 7 D 5 E 2 D 3 D 2 C 8 79 D 2 OD=0: 10 11 41 44 82 83 B 0 B 7 f 0 f 1 g 0 g 8 1 2 3 12 13 62 64 84 85 b 8 b 9 f 2 f 3 g 9 h 7 4 5 6 14 15 67 68 a 3 a 6 e 7 f 4 f 5 7 8 9 16 17 69 70 a 8 a 9 e 8 e 9 f 8 f 9 72 46 C 6 D 3 E 1 E 6 73 46 74 D 1 E 0 E 5 74 46 74 D 1 E 0 E 5 75 76 76 76 77 H 4 78 45 78 79 46 78 48 C 7 D 5 E 2 72 C 8 D 8 E 3 73 C 9 D 9 E 4 74 D 1 E 0 E 5 47 C 6 D 3 E 1 E 6 49 C 7 D 5 E 2 72 C 8 D 8 E 3 73 C 9 D 9 E 4 49 C 6 D 3 E 1 E 6 H 5 71 C 7 D 5 E 2 72 C 8 D 8 E 3 73 C 9 D 9 E 4 47 79 48 83 50 85 50 84 51 91 51 85 80 21 27 32 40 46 84 81 41 88 86 38 87 46 22 28 33 41 49 85 43 95 81 81 24 29 34 42 78 25 30 35 43 79 26 31 36 45 83 88 40 81 97 A 2 C 7 91 27 50 80 91 B 0 I 0 92 40 89 A 0 B 4 93 40 89 A 0 B 4 94 40 56 61 81 98 A 4 H 8 95 46 96 41 97 98 41 86 98 A 4 H 8 43 51 83 A 6 B 2 43 88 99 B 1 H 9 45 77 84 A 7 C 4 46 89 A 0 B 4 76 90 A 1 C 6 47 78 85 A 8 D 2 48 79 88 A 9 H 4 46 90 A 1 C 6 46 57 62 86 99 B 1 H 9 81 43 99 76 97 A 2 C 7 53 58 63 89 A 0 B 4 81 98 A 4 H 8 54 59 64 90 A 1 C 6 86 99 B 1 H 9 55 60 76 97 A 2 C 7 98 40 89 A 1 C 6 99 78 A 4 98 A 5 98 A 7 88 B 1 76 B 2 77 B 3 76 B 4 B 5 C 3 B 5 B 4 C 3 46 90 A 2 C 7 91 99 99 91 H 1 G 1 H 1 B 6 76 97 A 4 H 8 C 0 76 C 2 C 1 77 C 1 C 2 B 4 C 3 C 4 77 B 9 C 5 46 D 2 B 4 C 3 B 4 C 2 B 5 46 81 87 96 95 96 87 96 46 81 88 A 4 A 5 81 86 99 M A 0 B 1 B 4 H 9 A 5 A 4 A 3 H 4 C 0 C 1 C 2 B 6 C 0 C 1 C 2 B 5 H 1 B 5 C 3 B 6 C 1 B 6 C 0 H 5 C 0 C 1 B 2 B 7 B 8 C 4 51 78 B 2 D 1 H 7 C 6 40 46 72 73 74 E 0 40 46 72 73 74 H 9 76 81 86 89 90 97 98 99 A 0 A 1 A 2 A 4 B 1 B 4 C 7 A 2 A 3 A 4 B 1 B 2 I 0 C 8 C 9 D 1 D 3 D 5 C 6 C 7 C 8 C 9 D 1 D 8 D 9 E 0 E 1 E 2 D 3 D 5 D 8 D 9 E 1 E 3 E 4 E 5 E 6 H 8 E 2 E 3 E 4 E 5 E 6 H 9 H 8 H 9 E 1 46 72 73 74 81 C 7 40 46 72 73 74 87 95 96 C 7 76 81 86 89 90 C 8 C 9 D 1 D 3 D 5 97 98 99 A 0 A 1 D 8 D 9 E 0 E 2 E 3 A 2 A 4 B 1 B 4 C 6 E 4 E 5 E 6 C 8 C 9 D 1 D 3 D 5 D 8 D 9 E 0 E 1 E 2 46 72 73 74 C 6 E 3 E 4 E 5 E 6 H 8 C 7 C 8 C 9 D 1 D 3 H 9 D 5 D 8 D 9 E 0 E 1 E 3 E 4 E 5 E 6 C 8 46 72 73 74 81 87 95 96 C 7 E 3 46 72 73 74 C 6 C 9 D 1 D 3 D 5 D 8 C 7 C 8 C 9 D 1 D 3 D 9 E 0 E 1 E 2 E 3 D 5 D 8 D 9 E 0 E 1 E 4 E 5 E 6 E 2 E 4 E 5 E 6 C 9 41 43 46 81 88 E 4 46 72 73 74 C 6 D 0 46 72 73 74 81 C 7 C 8 C 9 D 1 D 3 C 6 C 7 C 8 C 9 D 1 D 5 D 8 D 9 E 0 E 1 D 3 D 5 D 8 D 9 E 0 E 2 E 3 E 5 E 6 E 1 E 2 E 3 E 4 E 5 D 5 46 72 73 74 C 6 E 6 H 0 H 1 H 2 H 3 C 7 C 8 C 9 D 1 D 3 H 4 H 5 H 6 H 7 H 8 D 5 D 8 D 9 E 0 E 1 D 1 41 43 46 72 73 E 2 E 3 E 4 E 6 74 81 88 C 6 C 7 D 6 46 72 73 74 C 6 C 8 C 9 D 1 D 3 D 5 C 7 C 8 C 9 D 1 D 3 D 8 D 9 E 0 E 1 E 2 D 5 D 8 D 9 E 0 E 1 E 3 E 4 E 5 E 6 E 2 E 3 E 4 E 5 D 2 45 47 48 49 78 G 1 H 4 79 91 E 7 E 8 E 9 F 0 G 5 G 6 D 3 46 72 73 74 C 6 C 7 C 8 C 9 D 1 D 5 G 6 46 81 H 0 H 1 H 2 D 8 D 9 E 0 E 1 E 2 H 3 H 4 H 5 H 6 H 7 E 3 E 4 E 5 E 6 H 8 D 4 46 72 73 74 C 6 H 0 46 81 H 2 H 3 C 7 C 8 C 9 D 1 D 3 D 5 D 8 D 9 E 0 E 1 H 4 H 5 H 6 H 7 H 8 E 2 E 3 E 4 E 5 E 6 H 1 D 5 46 72 73 74 C 6 46 81 H 0 H 2 H 3 C 7 C 8 C 9 D 1 D 3 H 4 H 5 H 6 H 7 H 8 D 9 E 0 E 1 E 2 H 2 46 81 G 1 H 0 H 1 E 3 E 4 E 5 E 6 H 3 H 4 H 5 H 6 H 7 D 6 46 72 73 74 C 6 H 8 C 7 C 8 C 9 D 1 D 3 D 5 D 8 D 9 E 0 E 1 H 3 44 H 9 E 2 E 3 E 4 E 5 E 6 E 8 H 4 45 47 48 50 51 D 7 46 72 73 74 91 77 91 G 1 I 0 C 6 C 7 C 8 C 9 D 1 H 5 46 76 81 H 0 H 1 D 3 D 5 D 8 D 9 E 0 E 1 E 2 E 3 E 4 E 5 H 2 H 3 H 6 H 7 H 8 E 6 H 6 46 81 H 0 H 1 H 2 D 8 46 72 73 74 C 6 H 3 H 5 H 7 H 8 C 7 C 8 C 9 D 1 D 3 D 5 D 9 E 0 E 1 E 2 H 8 40 46 76 81 86 E 3 E 4 E 5 E 6 E 9 89 90 97 98 99 D 9 40 46 72 73 74 A 0 A 1 A 2 A 4 B 1 76 81 86 89 90 B 4 C 6 C 7 H 0 H 1 97 98 99 A 0 A 1 H 2 H 3 H 5 H 6 H 7 A 2 A 3 A 4 B 1 B 2 H 9 C 6 C 7 C 8 C 9 D 1 D 3 D 5 D 8 E 0 E 1 E 2 E 3 E 4 E 5 E 6 H 8 H 9 41 44 46 81 87 88 95 96 H 4 43 46 78 79 81 H 0 H 1 H 2 H 3 H 5 H 7 H 8

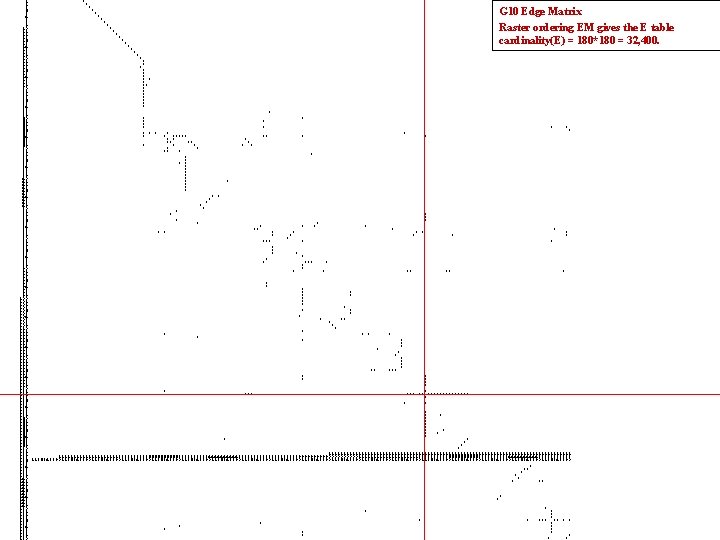
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14 * 15 * 16 * 17 * 18 * 19 * 20 * 21 * 22 * 23 * 24 * 25 * 26 * 27 * * 28 * 29 ** 30 * 31 * 32 * 33 * 34 * 35 * 36 * 37 38 * 39 40 * * 41 * * 42 * 43 * * 44 * 45 * * * 46 * * ***** ** * * 47 * * * 48 ** ** * 49 * * * 50 * * 51 ** * 52 * 53 * 54 * 55 * * 56 * 57 * 58 * 59 * 60 * 61 * * 62 * 63 * 64 * 65 66 * * 67 * 68 * 69 * 70 * 71 * 72 * * 73 * 74 * * 75 * * 76 * * 77 ** * * 78 * * * * 79 * * * 80 * 81 *** * * 82 83 * 84 * 85 * * 86 * 87 * 88 * *** * 89 * 90 * 91 * * ** ** * 92 93 94 95 * 96 * 97 * 98 * * 99 * * 100 * 101 * 102 * 103 * 104 * * 105 * 106 * 107 * ** 108 * 109 * 110 * 111 * 112 * * 113 * 114 * * 115 * 116 * 117 * 118 * 119 * 120 * 121 * 122 * 123 * 124 ** *** 125 126 * * 127 * * 128 * 129 * 130 131 * * 132 *** ** ******* 133 * 134 135 * * 136 137 138 * 139 * * 140 * 141 * 142 * 143 * 144 * * 145 * * 146 * 147 * * 148 * 149 * 150 * 151 11111111111111111111111111111111111111111 152 11111222223333344444555556666677777888889999900000111112222233333444445555566666777778 153 123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890 154 155 156 * 157 ** 158 * 159 * 160 * 161 * ** 162 163 164 165 166 * 167 * 168 169 170 * 171 * * 172 * 173 * 174 * * ** * * 175 * * 176 * * 177 * * 178 * * 179 * * G 10 Edge Matrix Raster ordering EM gives the E table cardinality(E) = 180*180 = 32, 400.

GN: S P P Ekey E C 1, 1 0 0 1, 2 1 5 1, 3 0 0 1, 4 0 0 1, 5 0 0 2, 1 1 5 2, 2 0 0 2, 3 1 5 2, 4 0 4 2, 5 1 5 3, 1 0 0 3, 2 1 5 3, 3 0 0 3, 4 1 4 3, 5 0 0 4, 1 0 0 4, 2 0 4 4, 3 1 4 4, 4 0 0 4, 5 1 4 5, 1 0 0 5, 2 1 5 5, 3 0 0 5, 4 1 4 5, 5 0 0 Remove edge with largest betweeness. Recalc betweenesses; Repeat. G 1_3 1 0 0 0 1 2 3 0 0 0 1 5 2 0 0 1 2 0 0 1 2 2 1 0 0 0 1 2 3 0 0 0 1 2 5 0 0 0 1 To construct SPPC(hk) =SPPC(kh) (Shortest Path Partic Count) if (hk) E ct 1 + Ct. S 2 P(hk) + Ct. S 2 P(kh) + Ct. S 3 P(hkg) + Ct. S 3 P(ghk), g + Ct. S 4 P(hkfm) + Ct. S 4 P(fhkm) + Ct. S 4 P(fmhk) f, m. Etc. 4 3 2 1 0 0 0 1 2 5 0 0 0 1 3 0 0 0 1 1 1 0 0 2 5 0 0 0 1 1 0 0 0 3 4 0 0 0 0 1 1 1 0 0 4 5 0 1 0 0 0 1 Use both a fore and aft p. Tree.