Gibbs Energy and Ellingham Diagrams Background G 0

Gibbs Energy and Ellingham Diagrams Background: G <0 · for a spontaneous change to be possible · a CLOSED SYSTEM · at constant temperature and pressure. 1

Under certain conditions Metal Oxide + CO (g) Metal + CO 2 (g) Under different conditions i. e. Metal + CO 2 (g) Metal oxide + CO(g) 2

· Equilibrium (i. e. state of maximum stability) will be attained in a closed system at constant temperature and pressure when G reaches its minimum possible value · At any temperature T*, G is given by G= H-T*. S · For chemical reactions involving gases the sign and magnitude of S is governed mainly by increase/decrease in number of gas moles, ie. If gas moles increase as a result of reaction then S>0, whereas if gas moles decrease then S<0. 3

Since G depends on both H and S then we have four possibilities H S G - + Always – at any T - - - where H > T S + + - where H < T S + - Always positive 4

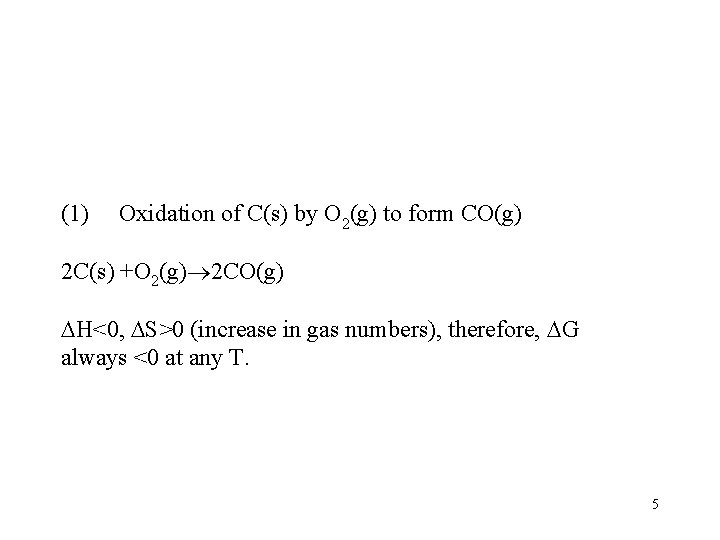
(1) Oxidation of C(s) by O 2(g) to form CO(g) 2 C(s) +O 2(g) 2 CO(g) H<0, S>0 (increase in gas numbers), therefore, G always <0 at any T. 5

2) Oxidation of a metal by O 2(g) e. g. 2 Al(s) + 3/2 O 2(g) Al 2 O 3 (s) H<0 (exothermic), S<0, provided T is low enough, then H > T S then G<0, reaction will work. But there will be a temperature at which G=0 and beyond which G is positive then metal oxide will decompose to metal and oxygen. 6

(3) Reaction between C(s) and CO 2(g) to CO(g) i. e. C(s) +CO 2(g) 2 CO(g) The reaction is endothermic ( H>0), but S is positive (increase in gas moles). If T is high enough reaction will occur. But if T is low enough the reverse reaction will occur. If H of reaction is positive and there is a decrease in number of gas moles from L to R then there can be no temperature where G become negative and reaction cannot occur spontaneously. 7

Variation of Go with temperature 8

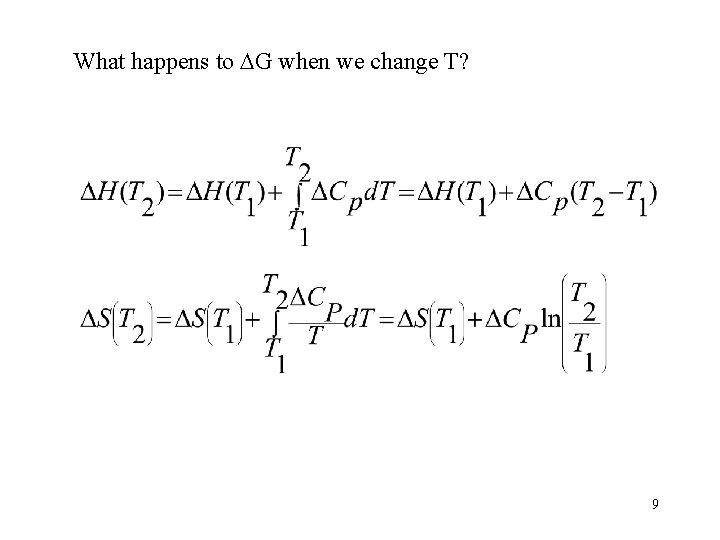
What happens to G when we change T? 9

Using these we can write at any temperature T* in terms of H(298 K) and S(298 k) and Cp. 10

But the 2 nd and fourth terms are usually small compared to the 1 st and 3 rd respectively AND here we are looking at the difference between these ( which will be even smaller) so we can write that: as a very good approximation for chemical reactions. 11

This means that G versus T is a straight line for many chemical reactions i. e. G= H-T S Rearrange G=-T S+ H, y=mx+c Where y= G, x=T slope m=- S, intercept C= H 12

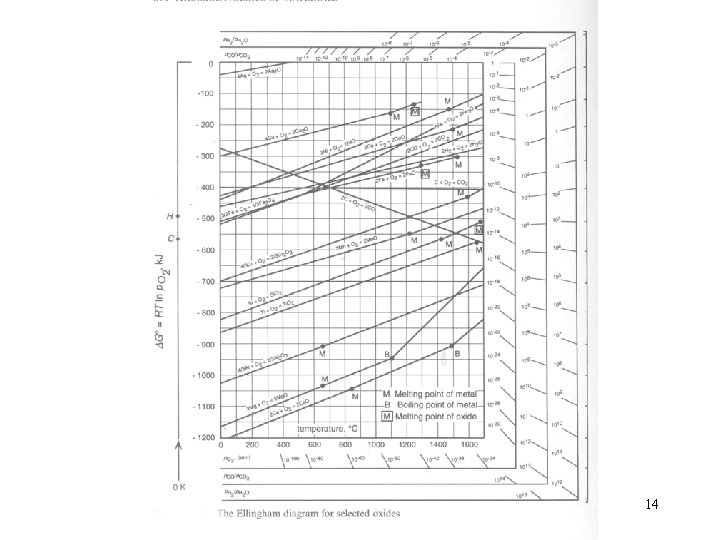
Plot several G’s on same diagram Ellingham Diagram ( r. Go plotted in each case for 1 mole of O 2(g)) The relation could be thus be expressed by 13

14

15

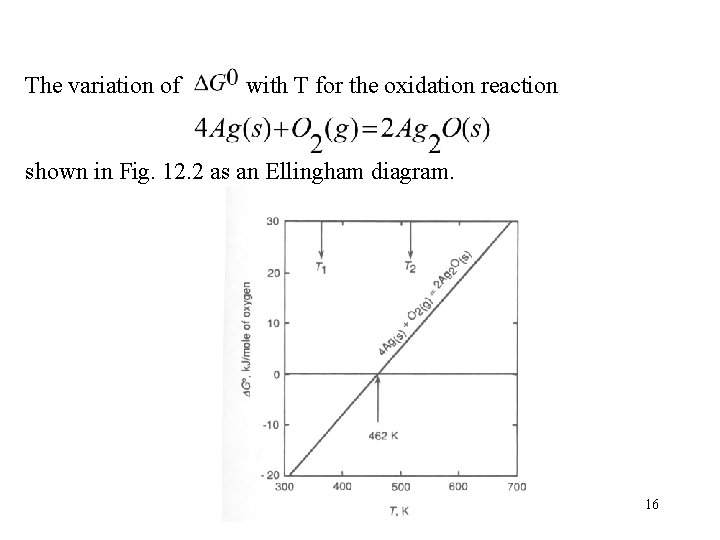
The variation of with T for the oxidation reaction shown in Fig. 12. 2 as an Ellingham diagram. 16

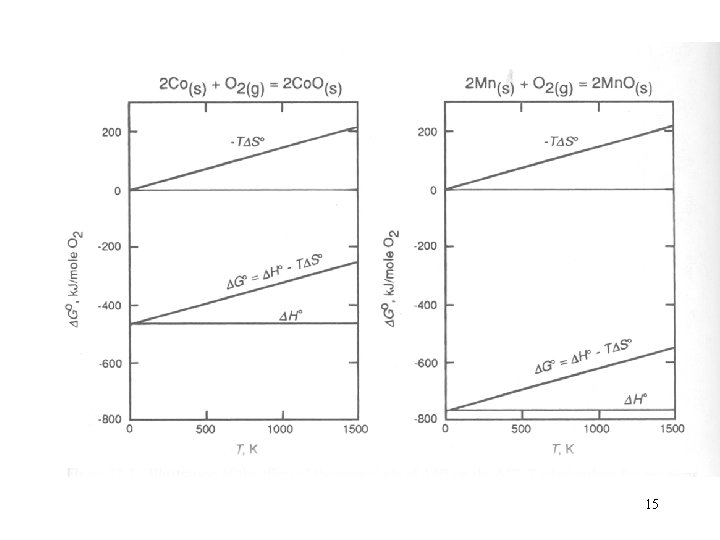
For the oxidation reaction 1. In the temperature range in which A and AO 2 are solid, is considerably greater than both and. Then 17

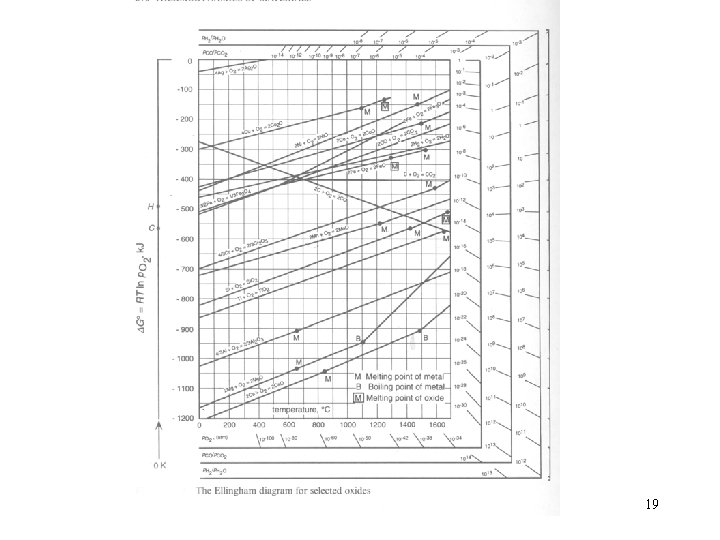
Thus the standard entropy change for oxidation reactions involving solid phase have almost the same value, which corresponds with the disappearance of 1 mole of oxygen gas initially at 1 atm pressure. As the slopes of the lines in an Ellingham diagram are equal to , then the lines are more or less parallel to one another, as will be seen in Fig. 12. 13. 18

19

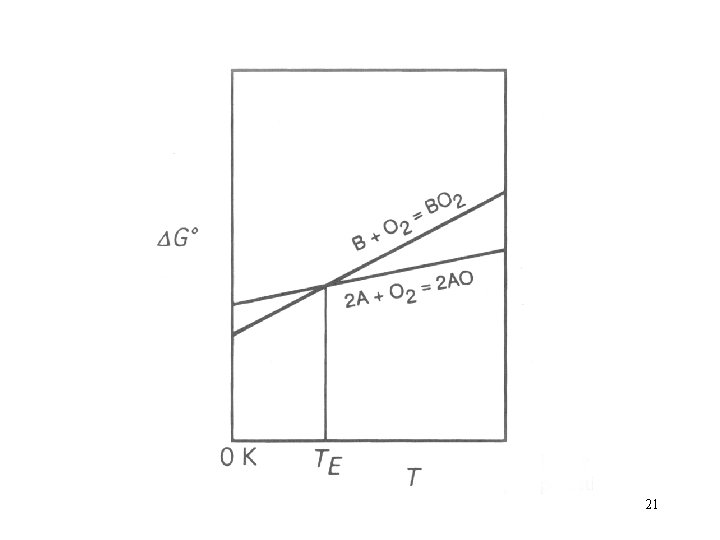
Consider two oxidation reactions, the Ellingham lines of which intersect one another, e. g. Which are shown in Fig. 12. 4. 20

21

is more negative than and that is more negative than. Subtraction of reaction (i) from reaction (ii) gives B+2 AO=2 A+BO 2 22

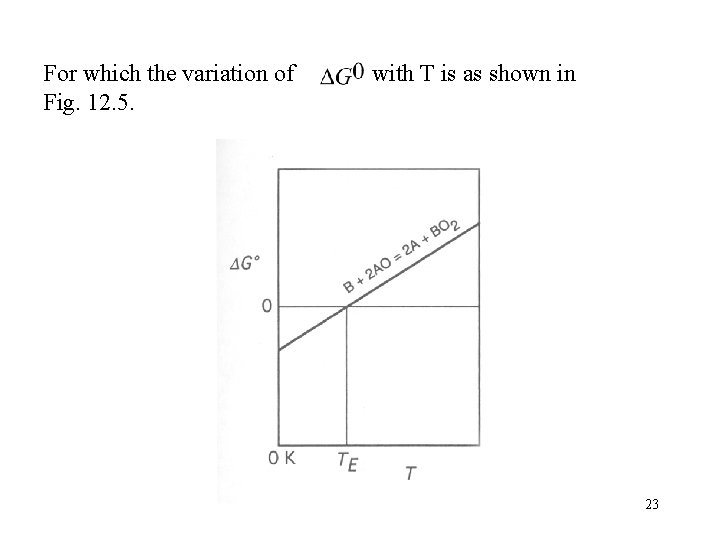
For which the variation of Fig. 12. 5. with T is as shown in 23

24