Getting started with Matlab Numerical Methods Appendix B

Getting started with Matlab Numerical Methods Appendix B http: //www. mathworks. com/access/helpdesk/ help/techdoc/learn_matlab. html

Linear Algebra with Matlab Introduction of Basic Matlab functions

n Solve n Ax=b n Matlab n x= Ab

trace(A) n >> A=[1 3 6; 2 1 9; 3 6 1] n A= n n n 1 2 3 3 1 6 n >> trace(A) n ans = n 3 6 9 1

rank() n n n n n >> B=[1 2 3; 3 4 7; 4 -3 1; -2 5 3; 1 -7 6] B= 1 2 3 3 4 7 Number of 4 -3 1 independent -2 5 3 rows 1 -7 6 >> rank (B) ans = 3

Reduced row echelon form; rref(B) n >> B=[1 2 3; 3 4 7; 4 -3 1; -2 5 3; 1 -7 6]; n >> rref(B) n ans = n n n 1 0 0 0 0 0 1 0 0

inv(A) n n n >> A=rand(3, 3) A= 0. 1389 0. 6038 0. 2028 0. 2722 0. 1987 0. 1988 0. 0153 0. 7468 0. 4451 >> inv(A) ans = -0. 8783 -8. 5418 14. 3617 1. 8694 1. 8898 -3. 2348 -0. 4429 2. 9695 -2. 7204 >> A*inv(A) ans = ? ? ?

det(A) n n n n >> A=rand(3, 3) A= 0. 9318 0. 8462 0. 4660 0. 5252 0. 4186 0. 2026 >> det(A) ans = 0. 0562 0. 6721 0. 8381 0. 0196

Ax=b; x=Ab n n n n n >> A=rand(3, 3) A= 0. 9318 0. 8462 0. 4660 0. 5252 0. 4186 0. 2026 >> b=rand(3, 1) b= 0. 1509 0. 6979 0. 3784 n n 0. 6721 0. 8381 0. 0196 n n n n >> x = Ab x= 3. 4539 -5. 4966 2. 3564 >> A*x ans = 0. 1509 0. 6979 0. 3784

tic, toc, elapsed_time n n >> tic >> toc elapsed_time = 2. 1630 n n >> tic >> x=toc x= 2. 5240

time. m n n A=rand(1000, 1000); tic inv(A); time_to_inverse_A=toc

output functions n n disp(‘strings to be shown on screen’); fprintf(‘As C language %8. 2 fn’, ver 1); n >> ver 1=1. 3333 >> fprintf('As C language %8. 2 fn', ver 1); n As C language 1. 33 n

norm(V, n) n n n n v=[3, 4] norm(v, 1) ans = 7 norm(v) ans = 5 n norm(v, 3) ans = 4. 4979 norm(v, inf) ans = 4 n ||V||1=(|v 1|+|V 2|+…|Vn| ) ||V||2=(|v 1|2+|V 2|2+…|V n|2 ) -2 ||V||3=(|v 1|3+|V 2|3+…|V n|3 ) -3 ||V||inf=(|v 1|∞+|V 2| ∞ +…|Vn| ∞) - ∞

If Ax=b has solution n Then Ax =0 only when x=0 n det(A) ≠ 0 n reff(A) = I n rank(A)=n n

LU decomposition n n >> A=rand(3) A= 0. 9991 0. 8848 0. 3593 0. 4178 0. 3566 0. 0836 >> [L 1, U]=lu(A) L 1 = 1. 0000 0 0. 3596 -0. 4291 0. 3569 1. 0000 n 0. 4642 0. 2477 0. 1263 n n n 0 1. 0000 0 n n n n U= 0. 9991 0. 8848 0 -0. 2322 0 0 n 0. 4642 -0. 0394 0. 0638 n n >> [L, U, P]=lu(A) L= 1. 0000 0 0. 3569 1. 0000 0. 3596 -0. 4291 0 0 1. 0000 U= 0. 9991 0 0 0. 8848 0. 4642 -0. 2322 -0. 0394 0 0. 0638 P= 1 0 0 0 1

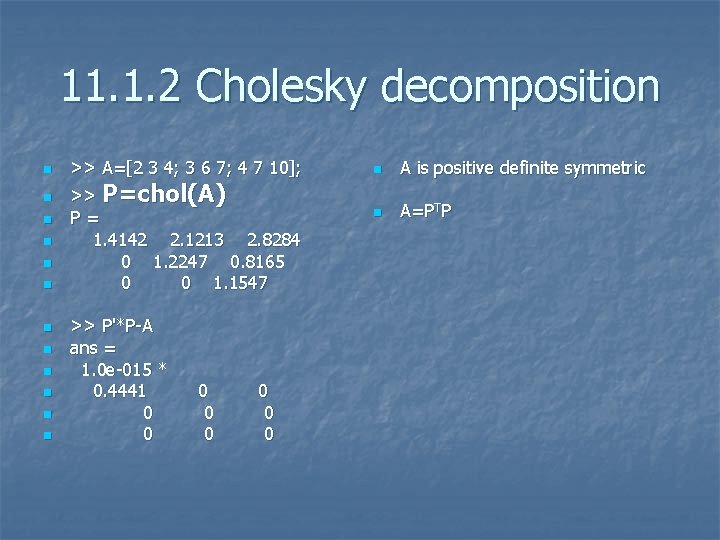
11. 1. 2 Cholesky decomposition n n n >> A=[2 3 4; 3 6 7; 4 7 10]; >> P=chol(A) P= 1. 4142 2. 1213 2. 8284 0 1. 2247 0. 8165 0 0 1. 1547 >> P'*P-A ans = 1. 0 e-015 * 0. 4441 0 0 0 0 n A is positive definite symmetric n A=PTP

QR decomposition n n n A= 0. 8138 0. 1635 0. 0567 0. 7576 0. 0536 0. 5092 0. 2240 0. 8469 0. 0466 >> [Q, R]=qr(A) Q= -0. 9781 -0. 0246 -0. 2065 -0. 1965 -0. 2161 0. 9564 -0. 0682 0. 9761 0. 2065 R= -0. 8319 -0. 7862 -0. 3887 0 0. 4667 -0. 1430 0 0 0. 7734 n Q n n R n Orthogonal matrix Upper triangle matrix

Singular Value Decomposition n >> U*S*V' ans = 1. 0000 5. 0000 2. 0000 n A=USVT n n n n n >> A = [1 2 3 4 5; 5 9 2 3 4; 2 2 3 4 2] n [U, S, V]=svd(A) n >> U= -0. 4581 0. 6831 -0. 5688 -0. 7993 -0. 5966 -0. 0727 -0. 3890 0. 4213 0. 8193 S= 14. 0087 0 0 0 5. 1976 0 0 0 1. 9346 n 0 0 0 V= -0. 3735 -0. 2803 0. 3650 -0. 4827 -0. 6447 -0. 6344 -0. 6080 -0. 0793 0. 2604 0. 3920 -0. 2955 0. 4079 0. 3133 -0. 5529 0. 5852 -0. 4130 0. 5056 0. 4052 0. 6063 -0. 2051 -0. 4473 0. 3601 -0. 7734 -0. 1609 -0. 2149 n n 3. 0000 2. 0000 3. 0000 A. . m x n U. . m x m S. . m x n n n 2. 0000 9. 0000 2. 0000 4. 0000 3. 0000 4. 0000 (singular value) V. . n x n 5. 0000 4. 0000 2. 0000

Reduce 3 columns n n n V= -0. 3735 -0. 2803 -0. 6344 -0. 6080 -0. 2955 0. 4079 -0. 4130 0. 5056 -0. 4473 0. 3601 n >> U*S*V' n ans = n n n 1. 4016 5. 0514 1. 4215 1. 9127 8. 9888 2. 1258 0 0 0 3. 3447 2. 0441 2. 5035 0 0 0 4. 4458 3. 0570 3. 3579 0 0 0 4. 1490 3. 8912 3. 2258

Pseudo-inverse n n n A= 0 0 0 1 n >> A*Aplus n ans = n n n >> Aplus=pinv(A) Aplus = 0 0 0 1 >> Aplus*A ans = 1 0 0 1 n n 0 0 0 0 0 1 0 0 0 1 Since A is not n by n, there is no inverse A-1. Ax=b can be solved by pseudo -inverse A+. x = A+ * b

cond(A), rcond(A) n n n >> A=eye(3). *20 A= 20 0 0 0 20 n cond(A) =1 n n n cond(A) > large number n n n >> [cond(A) rcond(A)] ans = 1 1 n A is perfectly conditioned stable A is ill-conditioned too sensitive rcond is a rapid version of cond n rcond~1/cond

Condition of a Hilbert matrix n n n n n >> hilb(4) ans = 1. 0000 0. 5000 0. 3333 0. 2500 0. 2000 >> cond(hilb(4)) ans = 1. 5514 e+004 0. 3333 0. 2500 0. 2000 0. 1667 0. 1429

Matlab Programming

if, else, and elseif if A > B 'greater' elseif A < B 'less' elseif A == B 'equal' else error('Unexpected situation') end

switch and case switch (rem(n, 4)==0) + (rem(n, 2)==0) case 0 M = odd_magic(n) case 1 M = single_even_magic(n) case 2 M = double_even_magic(n) otherwise error('This is impossible') end

for n = 3: 32 r(n) = rank(magic(n)); end r r Display the result

While a = 0; fa = -Inf; b = 3; fb = Inf; while b-a > eps*b (bisection method) x = (a+b)/2; fx = x^3 -2*x-5; if sign(fx) == sign(fa) a = x; fa = fx; else b = x; fb = fx; end x The result is a root of the polynomial x^3 - 2 x - 5 x = 2. 09455148154233

continue fid = fopen('magic. m', 'r'); count = 0; while ~feof(fid) line = fgetl(fid); if isempty(line) | strncmp(line, '%', 1) continue end count = count + 1; end disp(sprintf('%d lines', count));

break a = 0; fa = -Inf; b = 3; fb = Inf; while b-a > eps*b x = (a+b)/2; fx = x^3 -2*x-5; if fx == 0 break elseif sign(fx) == sign(fa) a = x; fa = fx; else b = x; fb = fx; end x

try - catch try statement. . . statement catch statement. . . end statement

return function d = det(A) %DET det(A) is the determinant of A. if isempty(A) d = 1; return terminates the current else sequence of commands and. . . returns control to the invoking end function

GUIDE

GUIDE

Blank GUI

M-file editor

Tools ->Run

GUI with Axes and Menu

Run

M-file editor

Try it yourself, and think about how to use it.