GERAK SATU DIMENSI 1 Kerangka Acuan Perpindahan Kecepatan










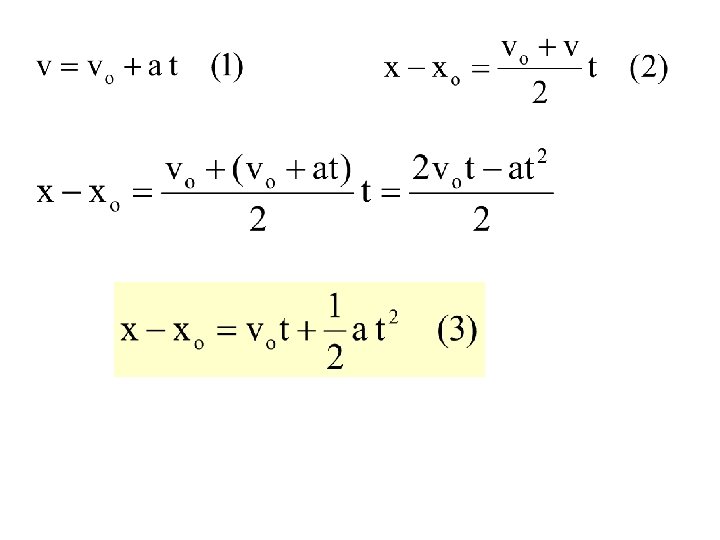
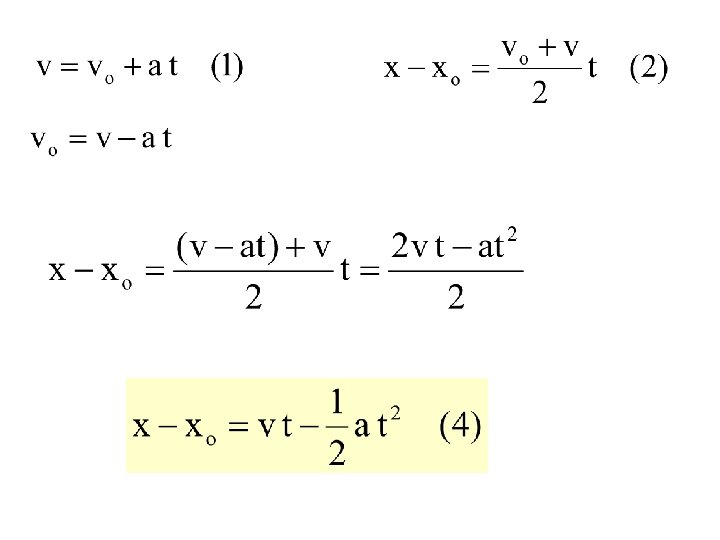
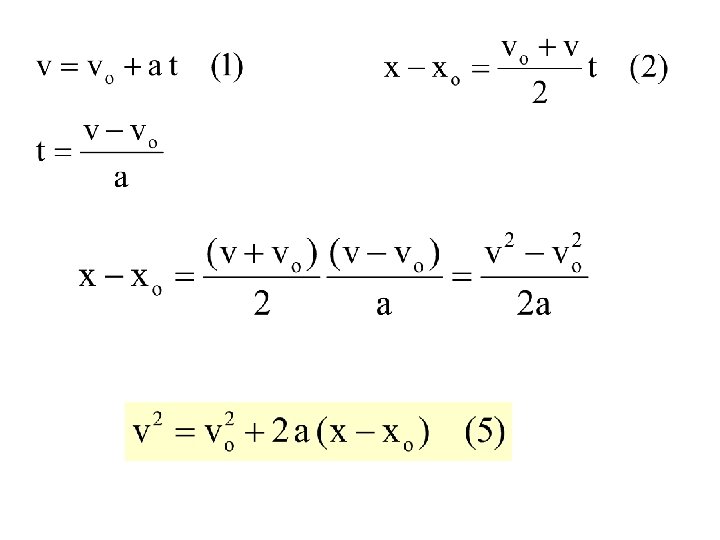










- Slides: 32

GERAK SATU DIMENSI 1

Kerangka Acuan Perpindahan Kecepatan Sesaat dan Rata-rata Percepatan Gerak dengan Percepatan Konstan Gerak Jatuh Bebas Analisa Grafik dari Gerak

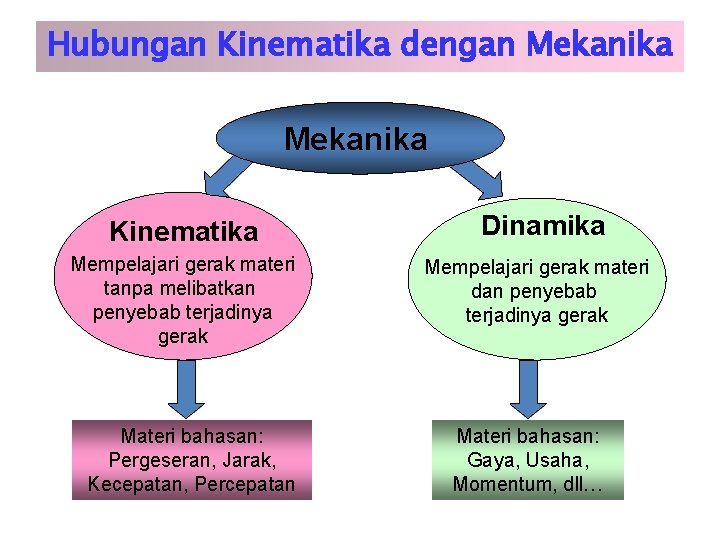
Hubungan Kinematika dengan Mekanika Kinematika Mempelajari gerak materi tanpa melibatkan penyebab terjadinya gerak Materi bahasan: Pergeseran, Jarak, Kecepatan, Percepatan Dinamika Mempelajari gerak materi dan penyebab terjadinya gerak Materi bahasan: Gaya, Usaha, Momentum, dll…

KINEMATIKA Ø Kinematika adalah bidang ilmu fisika yang mempelajari tentang gerak suatu obyek/benda tanpa memperhatikan penyebabnya • Bila suatu benda berubah posisinya (berpindah tempat) dalam kurun waktu tertentu, maka benda tersebut dikatakan mempunyai kecepatan • Bila suatu benda berubah kecepatannya dalam kurun waktu tertentu, maka benda tersebut dikatakan mempunyai percepatan q KECEPATAN DAN PERCEPATAN RATA-RATA x 1 = posisi awal x 2 = posisi akhir v 1 = kecepatan awal v 2 = kecepatan akhir t 1 = waktu awal t 2 = waktu akhir

q GERAK DENGAN PERCEPATAN KONSTAN Ø GERAK SATU DIMENSI § Gerak Horisontal § Gerak Vertikal (Jatuh Bebas) Ø GERAK DUA DIMENSI § Gerak Parabola (Peluru) § Gerak Melingkar § Gerak Relatip

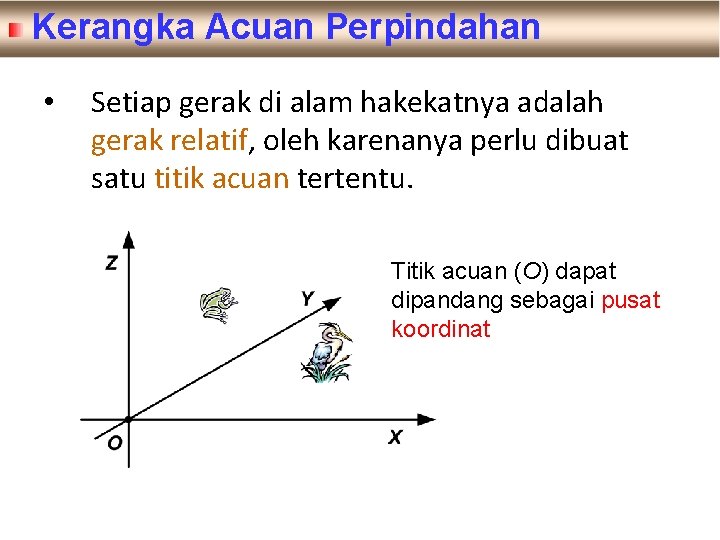
Kerangka Acuan Perpindahan • Setiap gerak di alam hakekatnya adalah gerak relatif, oleh karenanya perlu dibuat satu titik acuan tertentu. Titik acuan (O) dapat dipandang sebagai pusat koordinat

Kelajuan adalah Jarak yang ditempuh dalam selang waktu tertentu: Kecepatan Rata-rata adalah rate pergeseran dalam selang waktu tertentu: v : kecepatan r : rate pergeseran t : selang waktu Diperoleh dengan mengambil limit Δt 0.

Pesawat sedang melakukan gerak satu dimensi 8

Mobil di jalan tol sedang melakukan gerak satu dimensi 9

Kereta api sedang melakukan gerak satu dimensi 10

Gerak satu dimensi: Posisi benda dinyatakan secara lengkap dengan satu variabel saja Selanjutnya simbol vektor dapat dibuang Untuk gerak dua dimensi dan tiga dimensi, variabel posisi lebih dari satu Dua Dimensi Tiga Dimensi 11

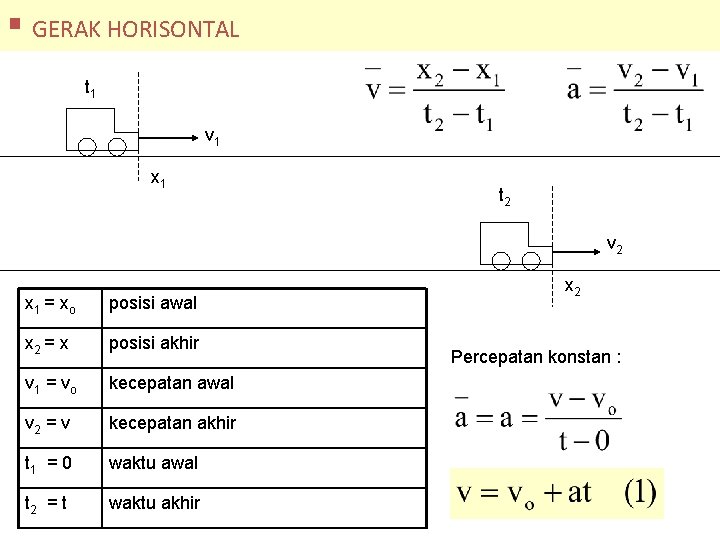
§ GERAK HORISONTAL t 1 v 1 x 1 t 2 v 2 x 1 = xo posisi awal x 2 = x posisi akhir v 1 = vo kecepatan awal v 2 = v kecepatan akhir t 1 = 0 waktu awal t 2 = t waktu akhir x 2 Percepatan konstan :

x 1 = xo posisi awal x 2 = x posisi akhir v 1 = vo kecepatan awal v 2 = v kecepatan akhir t 1 = 0 waktu awal t 2 = t waktu akhir Kecepatan rata-rata :
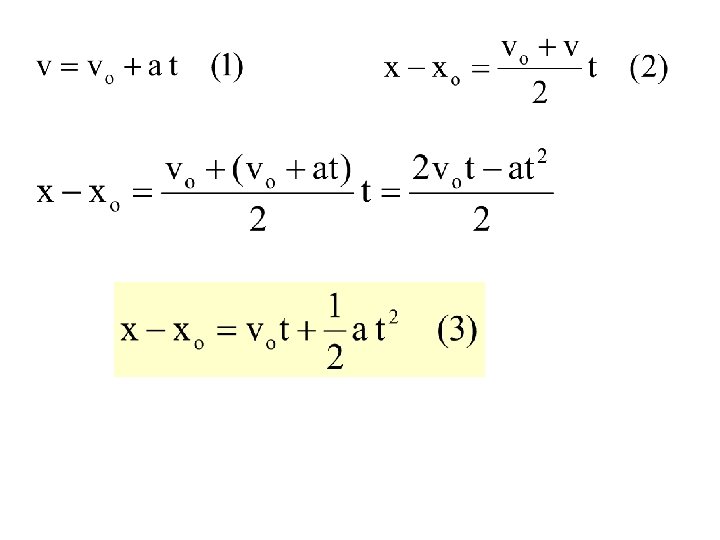
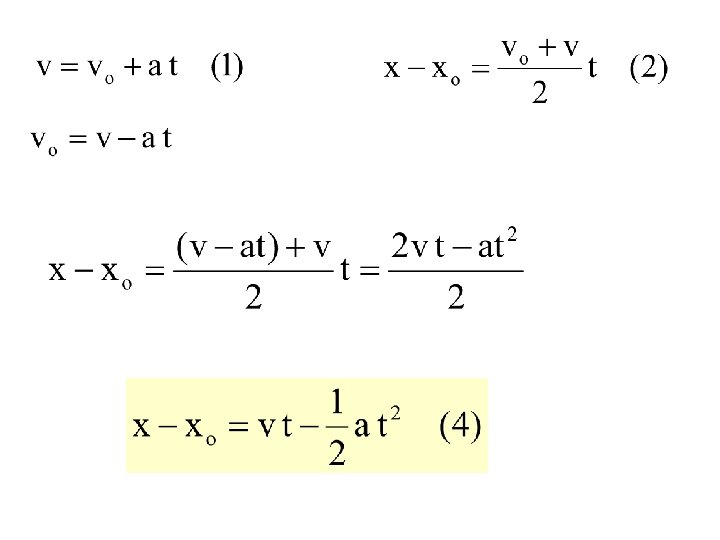
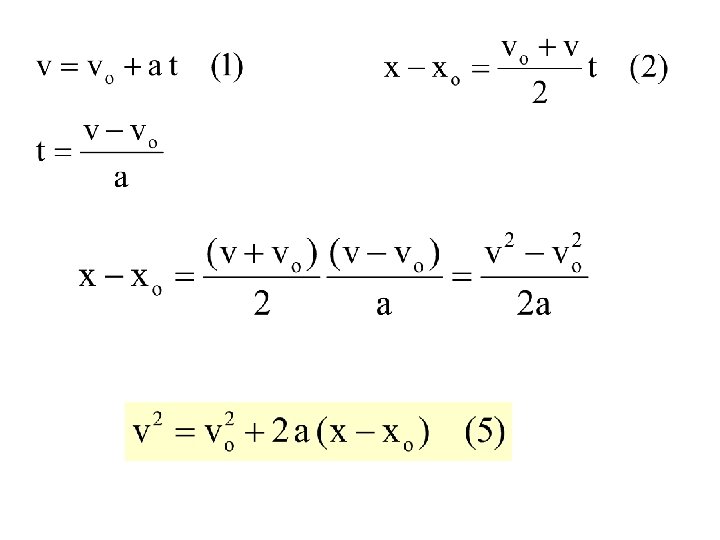

5 buah persamaan dengan 4 variabel

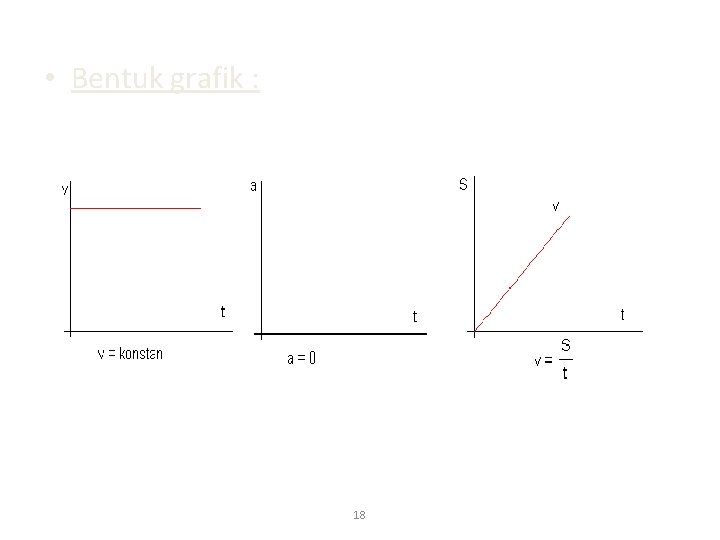
• Bentuk grafik : 18

Contoh Soal 1. 1 Sebuah pesawat jumbo jet memerlukan kecepatan minimum sebesar 360 km/jam agar dapat tinggal landas. Panjang landas pacu yang ada di bandar udara adalah 2000 m. a) Tentukan percepatan minimum yang harus dihasilkan oleh mesin jumbo jet tersebut. b) Berapa waktu yang diperlukan sebelum tinggal landas ? Jawab : Variabel yang sudah diketahui 3 : a). Untuk menghitung percepatan gunakan persamaan (5) :

b) Variabel yang diketahui 4 : (x-xo) , Vo , V dan a Untuk menghitung waktu dapat digunakan persamaan (2) : persamaan (1) :

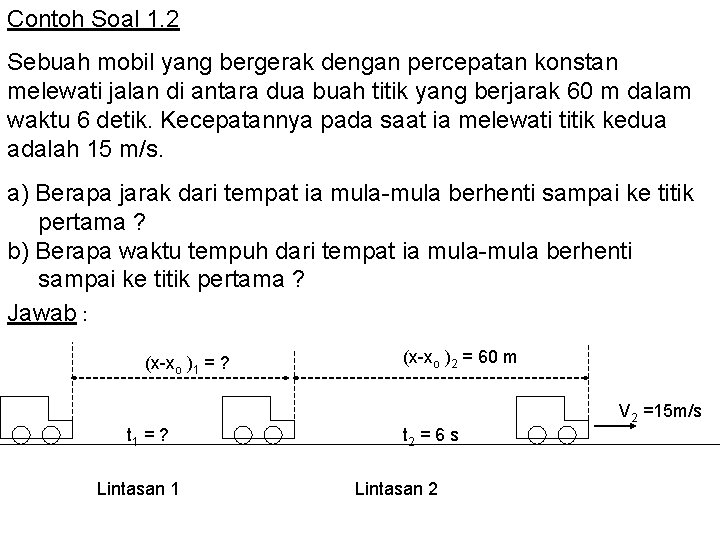
Contoh Soal 1. 2 Sebuah mobil yang bergerak dengan percepatan konstan melewati jalan di antara dua buah titik yang berjarak 60 m dalam waktu 6 detik. Kecepatannya pada saat ia melewati titik kedua adalah 15 m/s. a) Berapa jarak dari tempat ia mula-mula berhenti sampai ke titik pertama ? b) Berapa waktu tempuh dari tempat ia mula-mula berhenti sampai ke titik pertama ? Jawab : (x-xo )1 = ? (x-xo )2 = 60 m V 2 =15 m/s t 1 = ? Lintasan 1 t 2 = 6 s Lintasan 2

(x-xo)1 = ? t 1 = ? 60 m t 2 = 6 s V 2 =15 m/s Pada lintasan 1 hanya satu variabel yang diketahui, yaitu vo = 0 sehingga diperlukan 2 variabel lagi, yaitu percepatan dan kecepatan di titik 1(kecepatan awal pada lintasan 2 atau kecepatan akhir pada lintasan 1) Pada lintasan 2 sudah terdapat 3 besaran yang diketahui : (x-xo)2 = 60 m, kecepatan akhir V 2 = 15 m/s dan waktu t 2 = 6 s. Gunakan persamaan (2) pada lintasan 2 untuk menghitung Vo 2 :

60 m (x-xo)1 = ? t=? 5 m/s t=6 s 15 m/s Gunakan persaman (1) pada lintasan 2 untuk menghitung a : Pada lintasan 1 sudah terdapat 3 variabel yang diketahui a). Gunakan persaman (5) untuk menghitung x-xo b). Gunakan persaman (1) untuk menghitung t 1

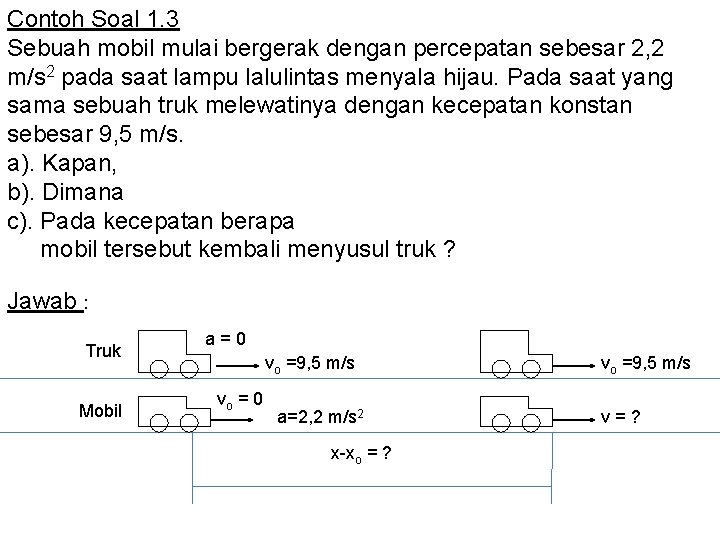
Contoh Soal 1. 3 Sebuah mobil mulai bergerak dengan percepatan sebesar 2, 2 m/s 2 pada saat lampu lalulintas menyala hijau. Pada saat yang sama sebuah truk melewatinya dengan kecepatan konstan sebesar 9, 5 m/s. a). Kapan, b). Dimana c). Pada kecepatan berapa mobil tersebut kembali menyusul truk ? Jawab : Truk Mobil a=0 vo =9, 5 m/s vo = 0 a=2, 2 m/s 2 x-xo = ? vo =9, 5 m/s v=?

Truk Mobil a=0 vo =9, 5 m/s vo = 0 a=2, 2 m/s 2 x-xo = ? a). b). c). vo =9, 5 m/s v=?

§ GERAK VERTIKAL (JATUH BEBAS) Persamaan dengan 4 variabel (y-yo), vo, v dan t Percepatan sudah diketahui a = - g

Contoh Soal 1. 4 Sebuah bola dilemparkan vertikal ke bawah dari atap sebuah gedung yang tingginya 36, 6 m. Dua detik kemudian bola tersebut melewati sebuah jendela yang terletak 12, 2 m di atas tanah a). Pada kecepatan berapa bola tersebut tiba di tanah ? b). Kapan bola tersebut tiba di tanah ? atap gedung Jawab : Gunakan persamaan (4) pada lintasan 1 (atap gedung jendela) : Vo 36, 6 jendela V 1 V 2 = ? tanah 12, 2

a). Gunakan persamaan (5) pada lintasan 2 (jendela tanah) : atap gedung Ambil yang negatip : v 2 = - 26, 9 m/s b). Gunakan persamaan (1) pada lintasan 2 : Vo 36, 6 jendela Vo 2 = - 22 Jadi tiba ditanah setelah 2, 5 s V 2 = ? tanah 12, 2

Contoh Soal 1. 5 Sebuah batu dilepaskan dari sebuah jembatan yang tingginya 50 m di atas permukaan sungai. Satu detik kemudian sebuah batu lain dilemparkan vertikal ke bawah dan ternyata kedua batu tersebut mengenai permukaan sungai pada saat yang bersamaan. Tentukan kecepatan awal dari batu kedua. Jawab : Gunakan persamaan (3) pada batu pertama : 2 1 Vo 1 = 0 Vo 2

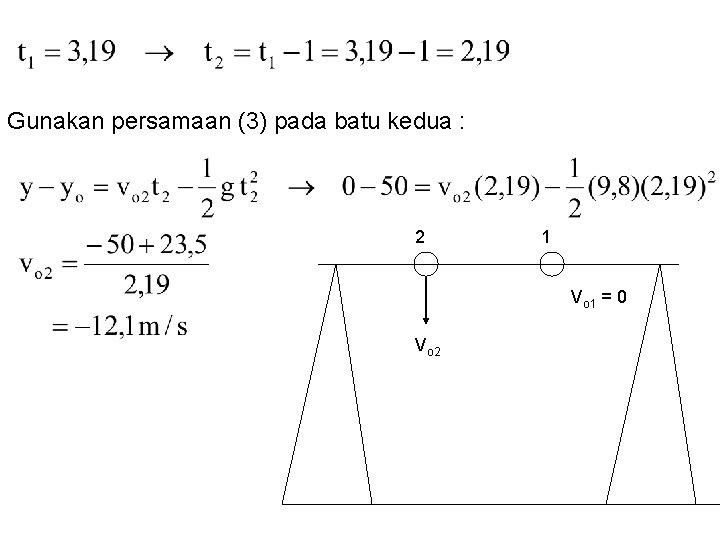
Gunakan persamaan (3) pada batu kedua : 2 1 Vo 1 = 0 Vo 2

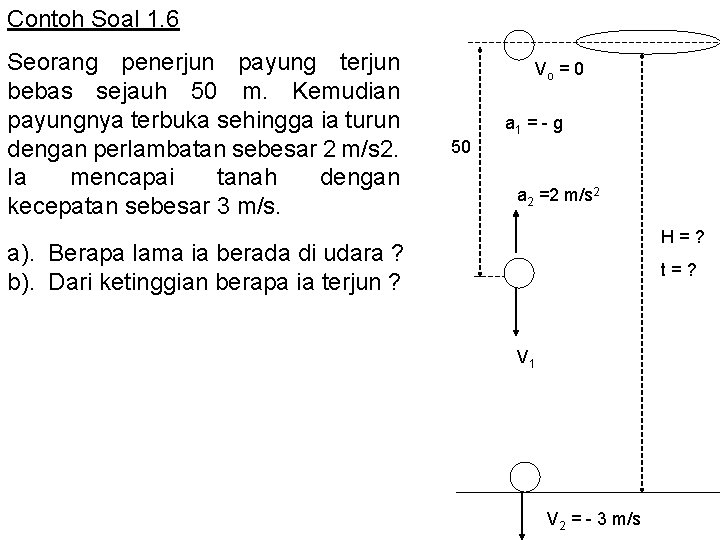
Contoh Soal 1. 6 Seorang penerjun payung terjun bebas sejauh 50 m. Kemudian payungnya terbuka sehingga ia turun dengan perlambatan sebesar 2 m/s 2. Ia mencapai tanah dengan kecepatan sebesar 3 m/s. Vo = 0 a 1 = - g 50 a 2 =2 m/s 2 H=? a). Berapa lama ia berada di udara ? b). Dari ketinggian berapa ia terjun ? t=? V 1 V 2 = - 3 m/s

Jawab : Gunakan persamaan (3) pada lintasan 1 : Vo = 0 50 V 1 Gunakan persamaan (1) pada lintasan 1 :
 Sebuah pesawat jumbo jet memerlukan kecepatan minimum
Sebuah pesawat jumbo jet memerlukan kecepatan minimum Acuan relatif adalah
Acuan relatif adalah Array 2 dimension
Array 2 dimension Contoh penilaian acuan norma dan penilaian acuan patokan
Contoh penilaian acuan norma dan penilaian acuan patokan Contoh profil posyandu doc
Contoh profil posyandu doc Kerangka acuan penelitian ilmiah
Kerangka acuan penelitian ilmiah Kerangka acuan posyandu remaja
Kerangka acuan posyandu remaja Kecepatan merupakan turunan dari
Kecepatan merupakan turunan dari Contoh soal kinematika partikel
Contoh soal kinematika partikel Dimensi organisasi adalah
Dimensi organisasi adalah Dimensi prosedural dan dimensi personal
Dimensi prosedural dan dimensi personal Dimensi dimensi etika komunikasi
Dimensi dimensi etika komunikasi Contoh dimensi formalisasi
Contoh dimensi formalisasi Deklarasi array 3 dimensi
Deklarasi array 3 dimensi Dimensi penelitian kualitatif
Dimensi penelitian kualitatif Contoh dimensi penelitian
Contoh dimensi penelitian Organ penyususn sistem gerak pada manusia adalah
Organ penyususn sistem gerak pada manusia adalah Three dimensional character
Three dimensional character Aliran mantap dan tak mantap
Aliran mantap dan tak mantap Tanda panjang dan pendek pada lagu potong bebek angsa
Tanda panjang dan pendek pada lagu potong bebek angsa Satu tahap arah pembelajaran maju-mundur dinamakan satu
Satu tahap arah pembelajaran maju-mundur dinamakan satu Definisi fungsi kuadrat
Definisi fungsi kuadrat Berkoresponden
Berkoresponden Daerah pertukaran tongkat estafet
Daerah pertukaran tongkat estafet Pengertian kalor adalah
Pengertian kalor adalah Dua plat hitam tak terhingga yang suhunya masing masing
Dua plat hitam tak terhingga yang suhunya masing masing Mind map perpindahan kalor
Mind map perpindahan kalor Rumus konduksi
Rumus konduksi Hukum fourier konduksi panas
Hukum fourier konduksi panas Perpindahan status dalam
Perpindahan status dalam Lintasan bagi perpindahan data antar modul disebut....
Lintasan bagi perpindahan data antar modul disebut.... Dampak perpindahan faktor produksi antar negara
Dampak perpindahan faktor produksi antar negara Sifat utama kurva ad dan perpindahan kurva ad
Sifat utama kurva ad dan perpindahan kurva ad