GeometryTrig Unit 7 Study Guide Name Date Unit

Geometry/Trig ________________ Unit 7 Study Guide Name: Date: _________________ Unit Goals: By the end of this unit, you should be able to… ü Identify the different polygons by shape and classification. ü Determine the sum of the interior and exterior angles of any polygon given the number of sides. ü Identify the 5 properties of a parallelogram. ü Be able to apply those properties to algebra problems and solve for parts of parallelograms. ü Identify the 5 ways to prove a quadrilateral is a parallelogram. ü Identify the three special parallelograms (rectangle, rhombus, and square). ü Distinguish between the properties for rectangles, squares and rhombi. ü Identify the properties of a trapezoid and apply them to algebra problems. ü Find the length of the median of a trapezoid. ü Find the area and perimeter of all quadrilaterals studied in this unit (formulas provided). Vocabulary: Polygon, Equilateral, Equiangular, Regular Polygon, Convex Polygon, Concave Polygon, Triangle, Quadrilateral, Pentagon, Hexagon, Heptagon, Octagon, Nonagon, Decagon, n-gon, Parallelogram, Rectangle, Square, Rhombus, Trapezoid, Median Property Parallelogram Rectangle Rhombus Square All angles are right angles Both Pairs of Opposite sides are parallel All sides are congruent Both Pairs of Opposite angles are congruent Diagonals bisect the interior angles of the quadrilateral Diagonals are perpendicular Diagonals are congruent Diagonals bisect one another Both Pairs of Opposite sides are congruent Area & Perimeter Practice for Quadrilaterals: § Rectangle & Square: p. 425 CE #3 -5; p. 427 WE #26 § Parallelogram & Rhombus: p. 431 CE #5, 7, 8; p. 431 WE #3, 4, 13, 14, 17 You will be given all of the formulas needed for area. § Trapezoid: p. 436 -437 WE #10 -15 Page 1

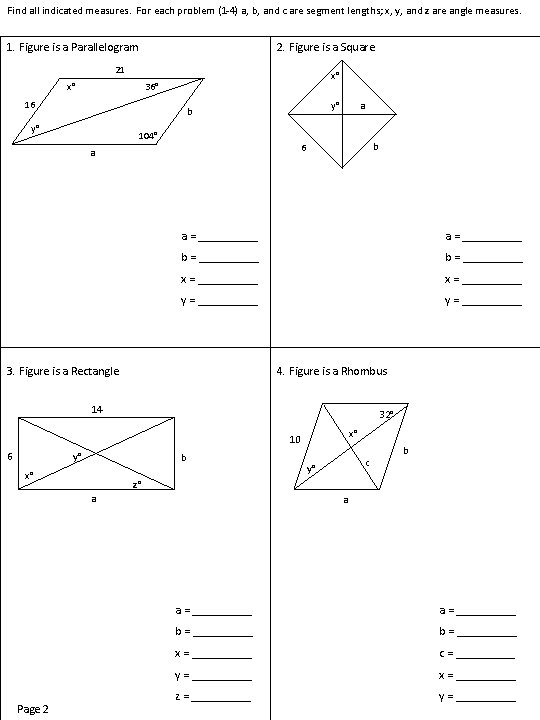
Find all indicated measures. For each problem (1 -4) a, b, and c are segment lengths; x, y, and z are angle measures. 1. Figure is a Parallelogram 2. Figure is a Square 21 x° x° 36° 16 y° b y° 104° a b 6 a a = __________ b = __________ x = __________ y = __________ 3. Figure is a Rectangle 4. Figure is a Rhombus 14 32° x° 10 6 y° b x° y° b z° a Page 2 c a a = __________ b = __________ x = _____ c = _____ y = _____ x = _____ z = _____ y = _____

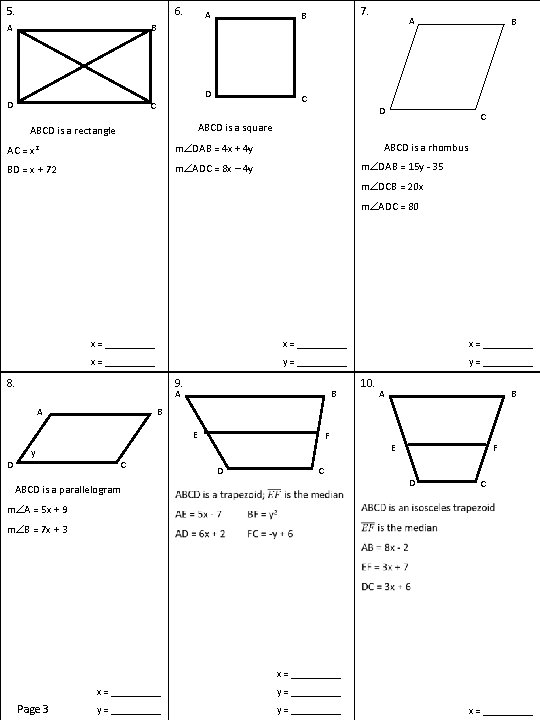
5. 6. A B D C 7. A D C ABCD is a square ABCD is a rectangle AC = x 2 mÐDAB = 4 x + 4 y BD = x + 72 mÐADC = 8 x – 4 y B ABCD is a rhombus mÐDAB = 15 y - 35 mÐDCB = 20 x mÐADC = 80 x = __________ y = __________ 8. 9. A A B B E D 10. y C F D C ABCD is a parallelogram E F D C mÐA = 5 x + 9 mÐB = 7 x + 3 x = _____ Page 3 x = __________ y = _____ x = _____

True and False _____1. All quadrilaterals are parallelograms. _____ 2. All parallelograms are quadrilaterals. _____ 3. All squares are rhombi. _____ 4. All rectangles are parallelograms. _____ 5. If diagonals of a quadrilateral bisect one another, then the quadrilateral is a parallelogram. _____ 6. All trapezoids are parallelograms. _____ 7. All parallelograms are rectangles. _____ 8. All trapezoids are quadrilaterals. _____ 9. All rhombi are squares. _____ 10. A square has congruent diagonals. _____ 11. A trapezoid can have four congruent sides. _____ 12. The diagonals of a rhombus are always congruent. _____ 13. All rectangles have perpendicular diagonals. _____14. Diagonals of a rhombus bisect one another. _____15. A trapezoid can have no congruent sides. Complete the blank with the word always, sometimes or never. 1. A square is _________ a rhombus. 2. The diagonals of a parallelogram ________ bisect one another. 3. A rectangle is __________ a square. 4. A square is __________ a rectangle. 5. A parallelogram ___________ has opposite congruent angles. 6. A rhombus is __________ a rectangle. 7. A rhombus ___________ has perpendicular diagonals. 8. A trapezoid is ____________ a parallelogram. 9. A rectangle ___________ has congruent diagonals. 10. A parallelogram ____________ congruent diagonals. 11. A parallelogram is ___________ a square. 12. A rectangle _____________ has perpendicular diagonals. 13. A rectangle is ______________ a rhombus. 14. A trapezoid __________ has two pairs of opposite parallel sides. 15. A square is ___________ a rhombus. 16. A rhombus is ___________ a square. 17. A rhombus ___________ has four right angles. 18. A parallelogram has interior angles that ______________ add up to 360˚. 19. A square is ___________ a trapezoid. Page 4

H T X M Determine whether the given information is enough to conclude that Quad. MATH is a parallelogram. If it is, write the method used. A Classify each figure as specifically as you can based on the markings in the diagram. 1. 2. 3. 4. 5. 6. Page 5