GeometryDefinitions Postulates Properties Theorems CH 3 Perpendicular Parallel

Geometry-Definitions, Postulates, Properties, & Theorems CH 3 -Perpendicular & Parallel Lines Geometry I

Navigating the Power. Point Takes you to the main menu Takes you to the help page There are other buttons explained throughout the Power. Point

Main Menu Click the buttons to navigate to the different slides (It’s best to follow the arrows) ✪ Background Info Quiz Info (next day) Theorems Quizlet (HW) Quiz (end of class) Theorems Cont. Helppp!! Basic Definitions Postulates

Background Info A theorem is a statement that has been proven on previously established statements like other theorems and postulates. A theorem is a proof of the truth of the resulting expression. A theorem is a logical argument in the sense that if a hypothesis is true then the conclusion must also be true. A postulate is a statement that is accepted without proof and is fundamental to a subject

Theorems NOTE: Click each theorem to take you to another slide with examples If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular If two sides of two adjacent acute angles are perpendicular, then the angles are complementary If two lines are perpendicular, then they intersect to form four right angles

Theorems Cont. Alternate Interior Angles: If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. Consecutive Interior Angles: If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary Alternate Exterior Angles: If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent

Postulates Note: Click each postulate to go to another slide with examples Parallel Postulate: If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line Perpendicular Postulate: If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line Corresponding Angles Postulate: If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.

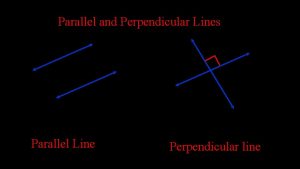
Basic Definitions NOTE: Click each definition to be directed to another slide with examples Parallel Lines-Two lines that are coplanar and do not intersect Skew Lines- Two lines that do not intersect and are not coplanar Transversal- A line that intersects two or more coplanar lines at different points Perpendicular Lines- Two lines intersect to form a right angle

Quizlet Homework (Print off a copy to bring to class) Go to quizlet. com Select create in the upper left-hand corner Make flashcards Create an account View the extra features Study your flashcards for the quiz tomorrow

Quiz Info Out of the 13 definitions only 5 will be on the quiz tomorrow. A mixture of the names and definitions will be placed in a cup. From there, you and your classmates will come to the front and choose one from the cup. If the name or part of the definition is drawn, the definition must be written (Pretty close to word-forword). If the definition is drawn, the name must be written. After the 5, students can raise their hands if they wish to continue with the quiz. It only takes 1 to force the class to answer more.

Helppp!! ✪ BI R T TC Ask peers P BD Read through book Look on You. Tube or Khan Academy Come see me before or after school Click the buttons around the slide for a description of each of the sections of the Power. Point (they are abbreviated). Q H Quizlet QI

BI (Background Info) This slide explains the definitions of theorems and postulates.

P (Postulates) The first three of the chapter are given along with their definitions. Click the postulate to take you to another slide where examples are presented.

T (Theorems) The first six theorems of the chapter are given along with their definitions. Click theorem to take you to another slide where examples are presented.

TC (Theorems Cont. ) This slide is a continuation of the previous theorems slide.

BD (Basic Definitions) Four definitions are given. Buttons take you to another slide where visuals are displayed.

Q (Quiz) This slides provides a link to take you to the end of the presentation where there will be a short quiz. The quiz will not be graded, but try your best because it is great practice for the quiz tomorrow!

QI (Quiz Info) This slide provides information on and the expectations for the quiz the following day.

Qui-zlet (Quizlet) This slide provides a brief explanation on how to use Quizlet and what is expected for the homework for the following day.

H (Helppp!!) This slide presents ways to get extra assistance if needed. It also provides buttons for each of the sections, which take you to another slide that describes each of the sections. The titles of the buttons are abbreviated by the first letter of each word.

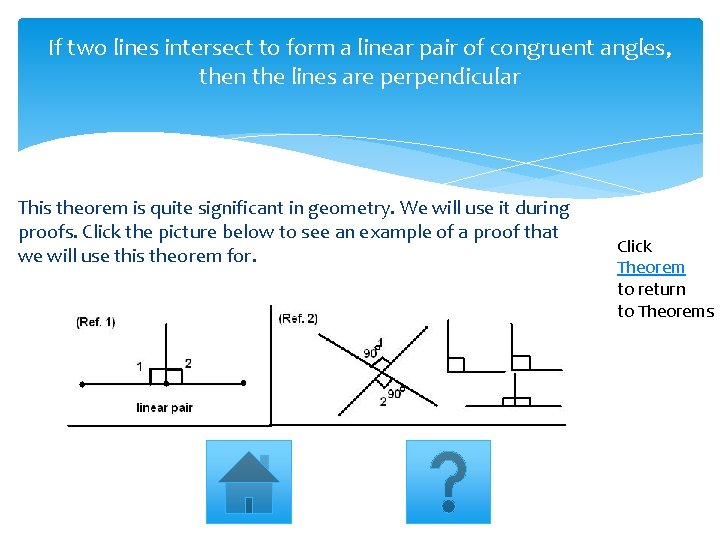
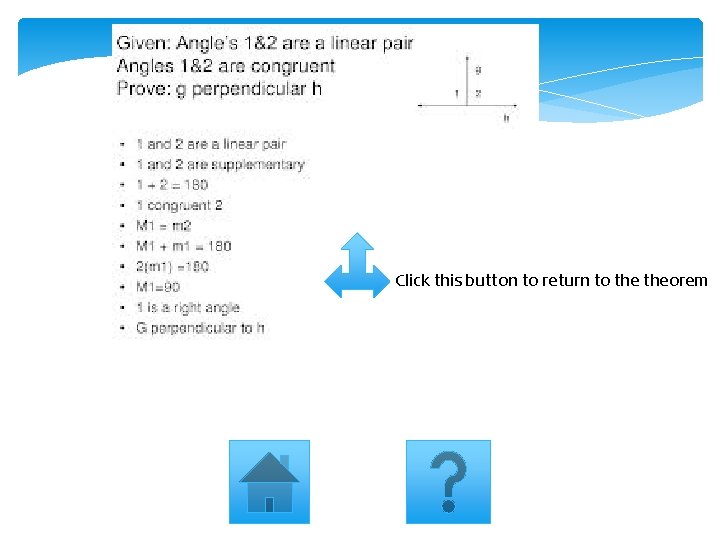
If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular This theorem is quite significant in geometry. We will use it during proofs. Click the picture below to see an example of a proof that we will use this theorem for. Click Theorem to return to Theorems

If two sides of two adjacent acute angles are perpendicular, then the angles are complementary Click Theorem To return to Theorems Below is a link to a video of a proof that we will solve in this class Video Proof

If two lines are perpendicular, then they intersect to form four right angles Click Theorem to return to Theorems Using this theorem and the definitions of perpendicular lines and right angles, you will be able to write different kinds of proofs for the same situation. Proof Hints: • Use definition of perpendicular lines to find one right angle. • Use vertical and linear pairs of angles to find three more right angles.

Alternate Interior Angles: If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. Click TC to return to Theorems Cont. Click on the link below to watch a video on the proof of theorem. AIA

Consecutive Interior Angles: If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary Click TC to return to Theorems Cont. Click on the link to watch a video on a proof CIA

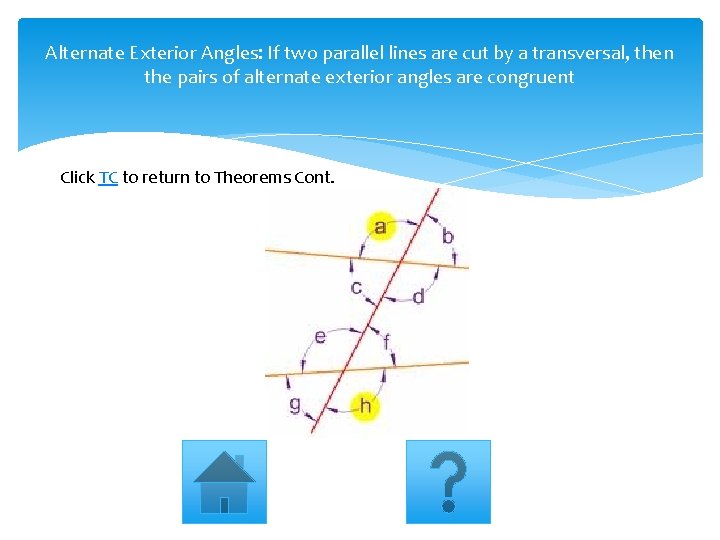
Alternate Exterior Angles: If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent Click TC to return to Theorems Cont.

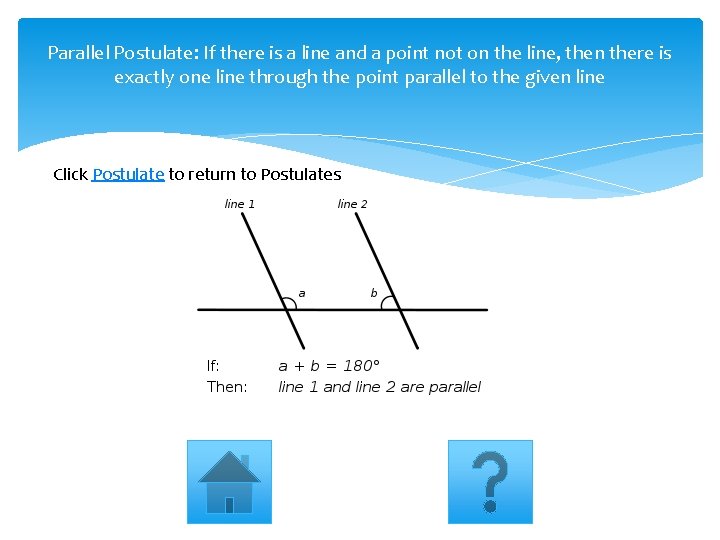
Parallel Postulate: If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line Click Postulate to return to Postulates

Perpendicular Postulate: If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line If we wanted to measure the distance between a point and a line, we can employ the Perpendicular Postulate, a compass, and a straightedge, since there exists only one perpendicular line from a point to a line. Click the button below for an example: Click Postulate to return to Postulates

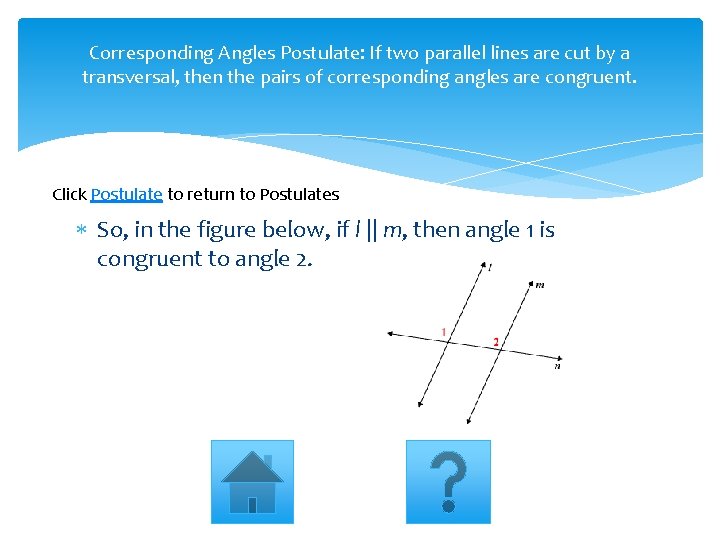
Corresponding Angles Postulate: If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent. Click Postulate to return to Postulates So, in the figure below, if l || m, then angle 1 is congruent to angle 2.

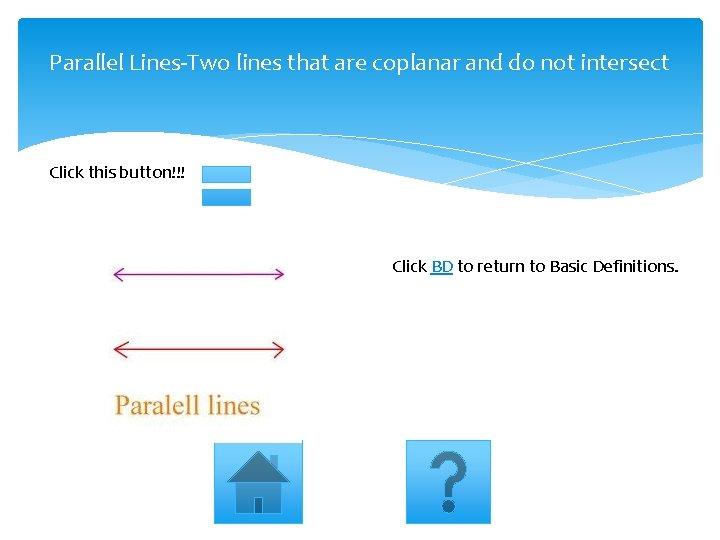
Parallel Lines-Two lines that are coplanar and do not intersect Click this button!!! Click BD to return to Basic Definitions.

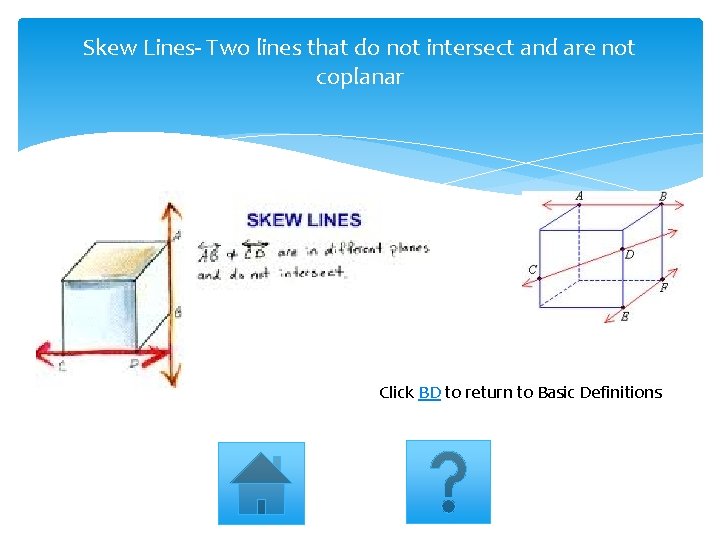
Skew Lines- Two lines that do not intersect and are not coplanar Click BD to return to Basic Definitions

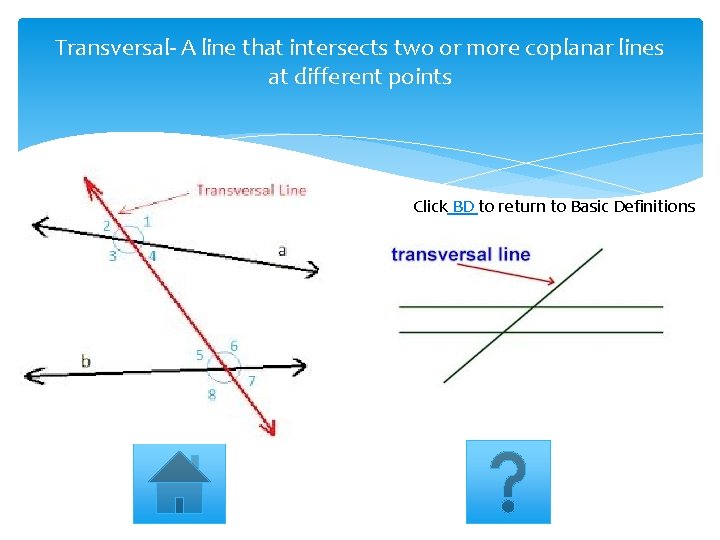
Transversal- A line that intersects two or more coplanar lines at different points Click BD to return to Basic Definitions

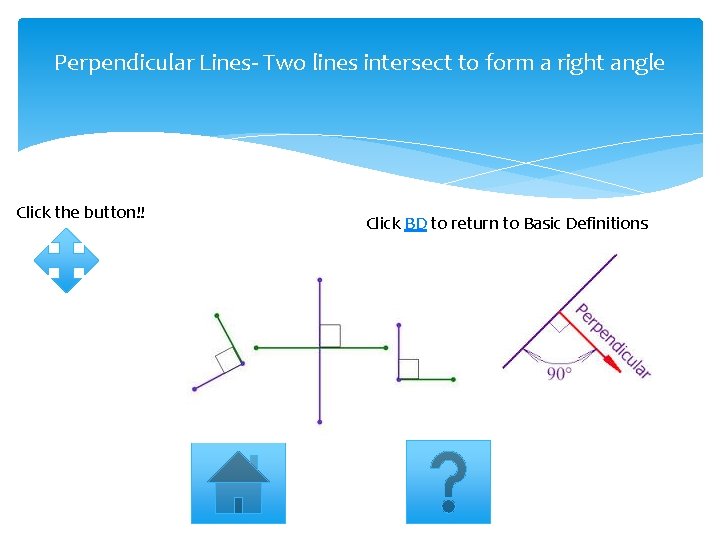
Perpendicular Lines- Two lines intersect to form a right angle Click the button!! Click BD to return to Basic Definitions

Click this button to return to theorem

The next few slides are a short quiz that will not be graded, but it is great practice for tomorrow’s quiz! This quiz is meant to be completed after you have gone through the full Power. Point. You must answer the questions correctly before moving on to the next question Click the Start button to begin Start

Question 1 True or False: This is the correct definition of parallel lines: Two lines are parallel if and only if they do not intersect. Click True or False True False

Return to ? Move to next ?

*Hint: There is a key word missing from the definition. Think about the definition of skew lines and how the two differ. Return to the ?

Question 2 True or False: A postulate is a statement that is accepted without proof and is fundamental to a subject True False

Return to the ? Next ?

*Hint: You’ll find the answer on the Background Info slide Return to the ?

Question 3 Fill in the blank: If two sides of two adjacent acute angles are perpendicular, then the angles are ____ A. Complementary B. Supplementary C. Obtuse

Return to the ? Next ?

*Hint: Refer to the Theorems slide Return to the ?

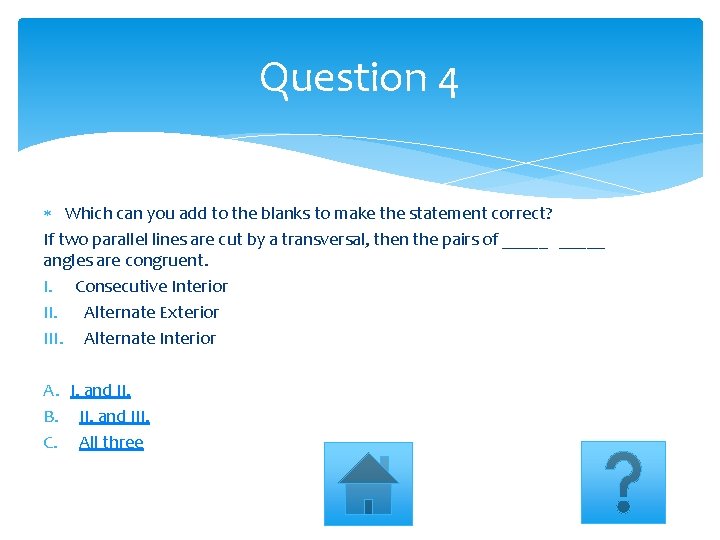
Question 4 Which can you add to the blanks to make the statement correct? If two parallel lines are cut by a transversal, then the pairs of _____ angles are congruent. I. Consecutive Interior II. Alternate Exterior III. Alternate Interior A. I. and II. B. II. and III. C. All three

Return to the ? Next ?

*Hint: Check out theorems Return to the ?

Question 5 What makes the following statement incorrect? A theorem is a statement that hasn’t been proven on previously established statements like other theorems and postulates. A. Proven B. Statements C. Hasn’t

Return to the ? End

*Hint: Is a theorem a proven statement? Return to the ?

You have completed the lesson! Remember to study for your quiz!

References

References Cont.

References Cont.

References Cont.