GEOMETRY TRANSFORMATION Reflection 8 th Math Presented by
GEOMETRY TRANSFORMATION Reflection 8 th Math Presented by Mr. Laws

Standard 8. G. 3 - Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.

Essential Question How can I describe the effect of reflecting a two-dimensional figure on a coordinate plane?

Target Statment Ø I CAN reflect a two-dimensional figure across the x-axis of a coordinate plane. Ø I CAN reflect a two-dimensional figure across the y-axis of a coordinate plane.

What is Reflection? 1. A reflection is a transformation that flips an object across a line of reflection (in a coordinate grid the line of reflection may be the x or y axis). 2. The reflected image is the mirror image of the original two-dimensional image. 3. The original image can be flip horizontally across the x-axis or flip vertically across yaxis.
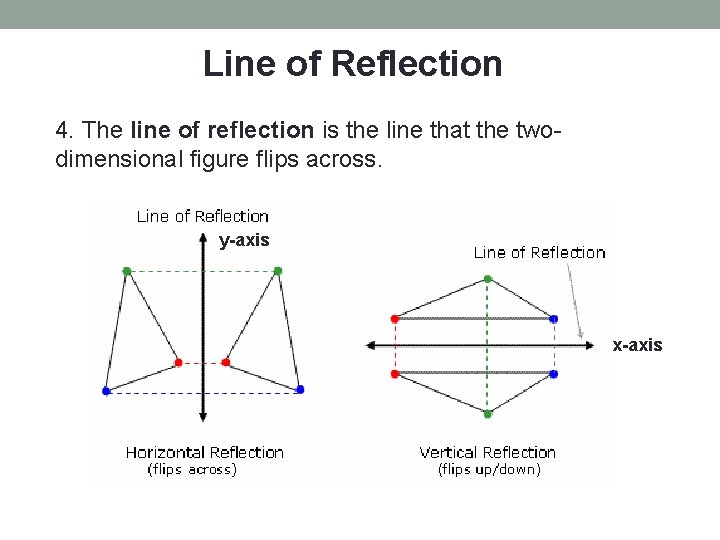
Line of Reflection 4. The line of reflection is the line that the twodimensional figure flips across. y-axis x-axis
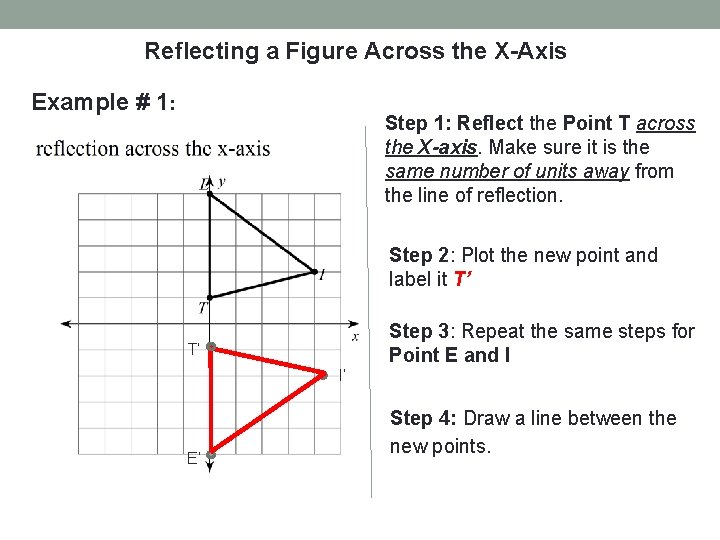
Reflecting a Figure Across the X-Axis Example # 1: Step 1: Reflect the Point T across the X-axis. Make sure it is the same number of units away from the line of reflection. Step 2: Plot the new point and label it T’ T’ I’ E’ Step 3: Repeat the same steps for Point E and I Step 4: Draw a line between the new points.
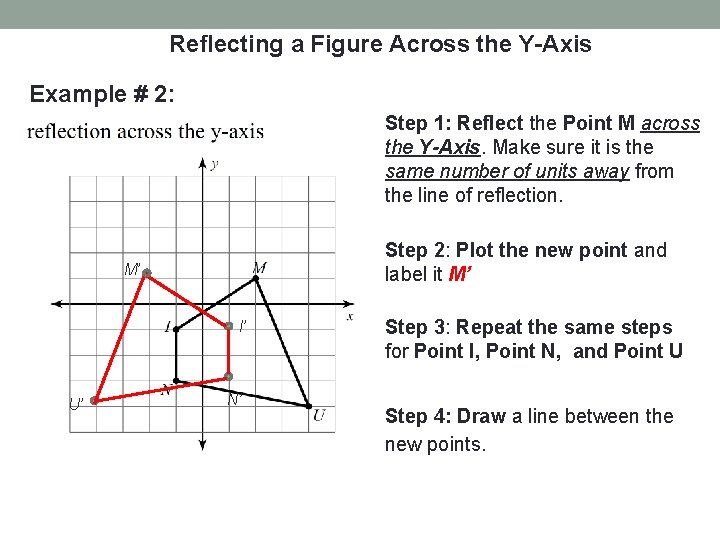
Reflecting a Figure Across the Y-Axis Example # 2: Step 1: Reflect the Point M across the Y-Axis. Make sure it is the same number of units away from the line of reflection. Step 2: Plot the new point and label it M’ M’ I’ U’ N’ Step 3: Repeat the same steps for Point I, Point N, and Point U Step 4: Draw a line between the new points.

Example # 3: What are the new coordinates after the figure has been transformed by reflection?
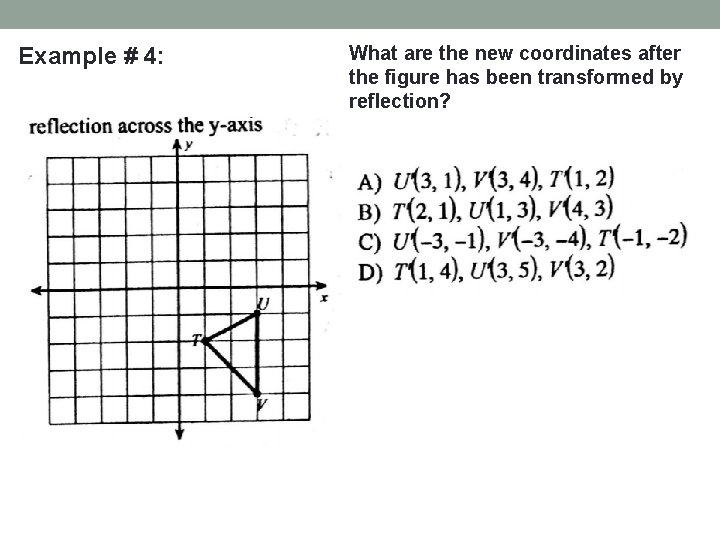
Example # 4: What are the new coordinates after the figure has been transformed by reflection?

Summary • What are some important steps to remember about reflecting a two-dimensional figure on a coordinate plane?
- Slides: 11