Geometry Topic 4 Quadrilaterals and Coordinate Proof Vocabulary

Geometry Topic 4 Quadrilaterals and Coordinate Proof

Vocabulary

Mathematically Speaking! Choose 3 -4 vocabulary words for the day. Throughout the lesson, as students respond to your questions or are presenting a problem on the board, mark a tally when a vocabulary word is used accurately. This can be turned into a competition among groups or between periods. Examples of accuracy • line vs line segment • translation vs slide • midpoint vs the middle

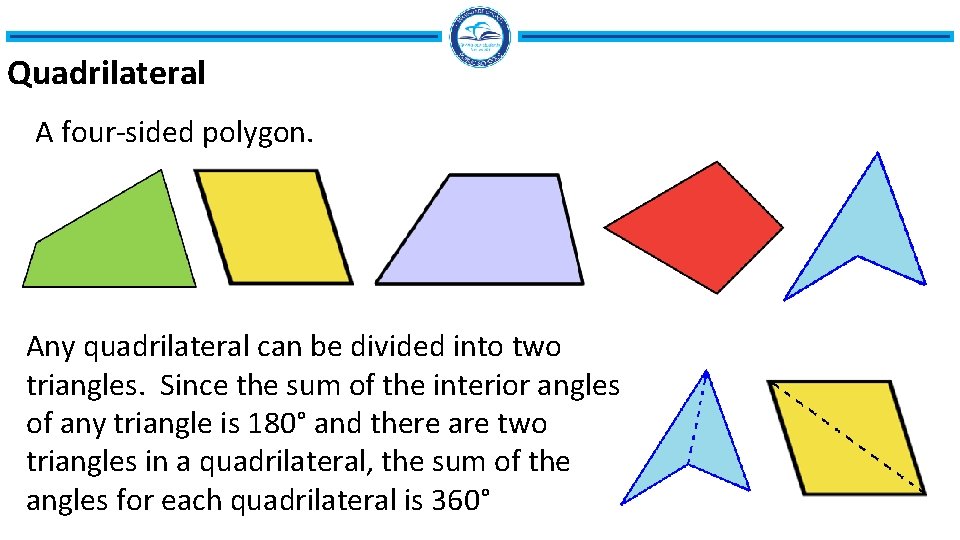
Quadrilateral A four-sided polygon. Any quadrilateral can be divided into two triangles. Since the sum of the interior angles of any triangle is 180° and there are two triangles in a quadrilateral, the sum of the angles for each quadrilateral is 360°

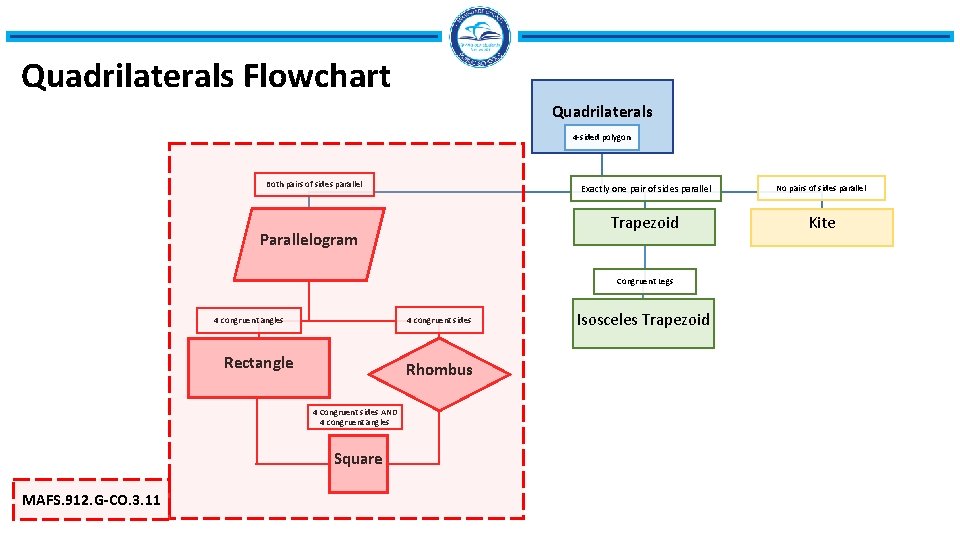
Quadrilaterals Flowchart Quadrilaterals 4 -sided polygon Both pairs of sides parallel Parallelogram Exactly one pair of sides parallel No pairs of sides parallel Trapezoid Kite Congruent Legs 4 congruent sides 4 congruent angles Rectangle Rhombus 4 Congruent sides AND 4 congruent angles Square MAFS. 912. G-CO. 3. 11 Isosceles Trapezoid

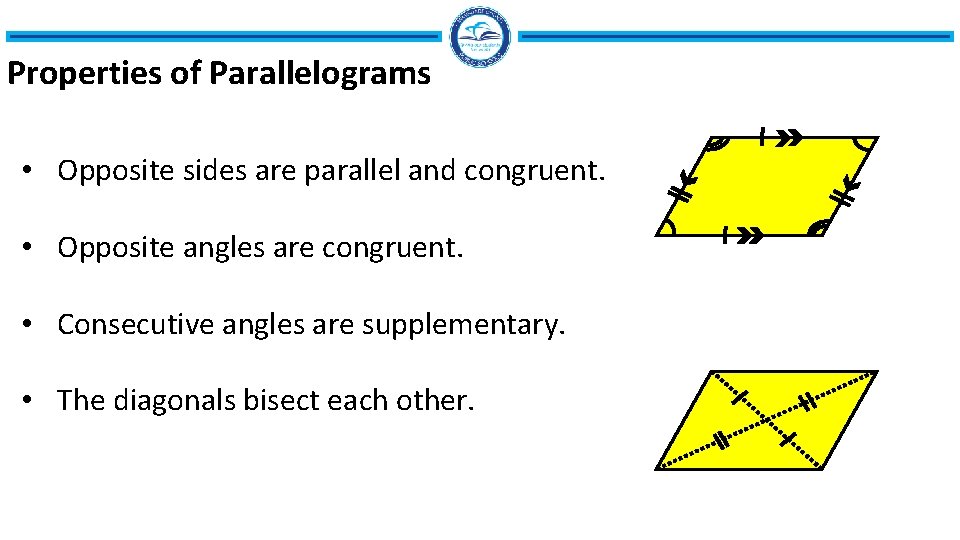
Properties of Parallelograms • Opposite sides are parallel and congruent. • Opposite angles are congruent. • Consecutive angles are supplementary. • The diagonals bisect each other.

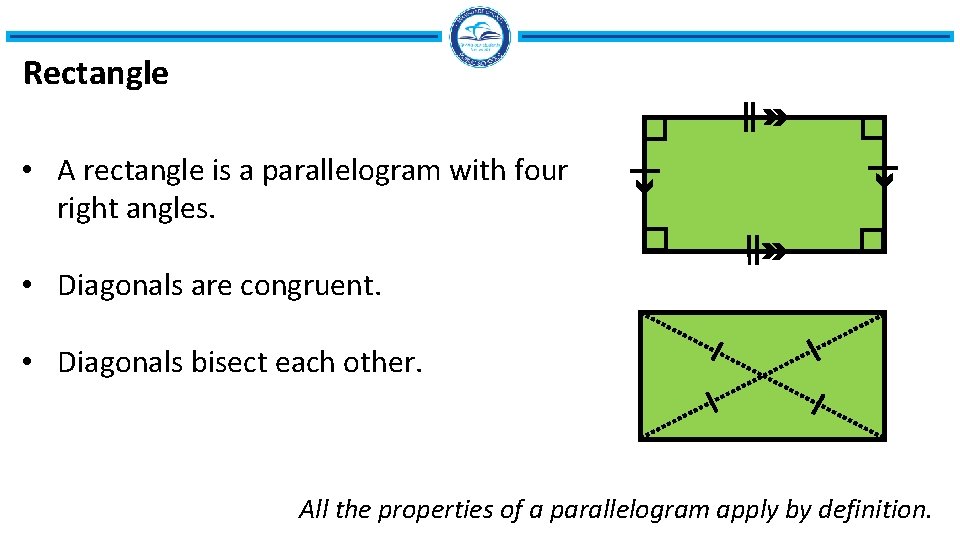
Rectangle • A rectangle is a parallelogram with four right angles. • Diagonals are congruent. • Diagonals bisect each other. All the properties of a parallelogram apply by definition.

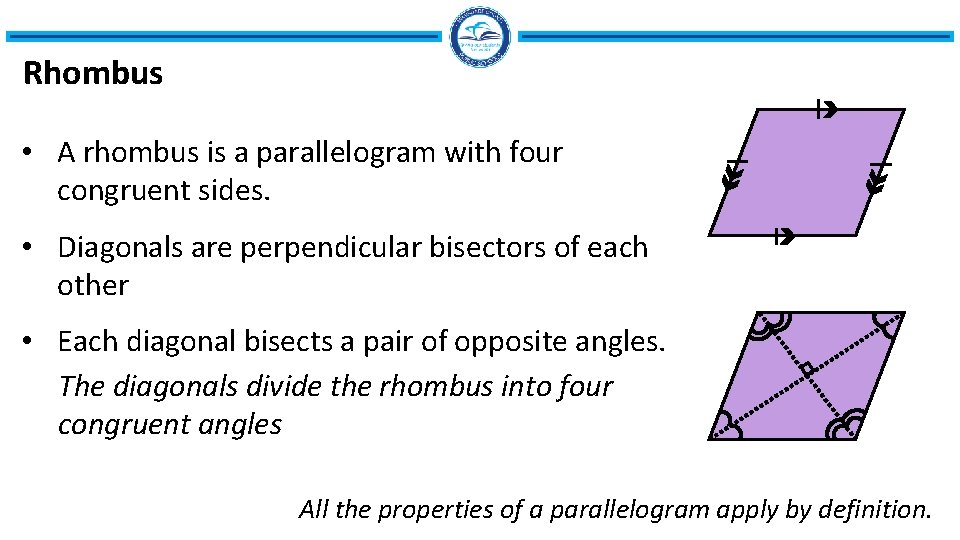
Rhombus • A rhombus is a parallelogram with four congruent sides. • Diagonals are perpendicular bisectors of each other • Each diagonal bisects a pair of opposite angles. The diagonals divide the rhombus into four congruent angles All the properties of a parallelogram apply by definition.

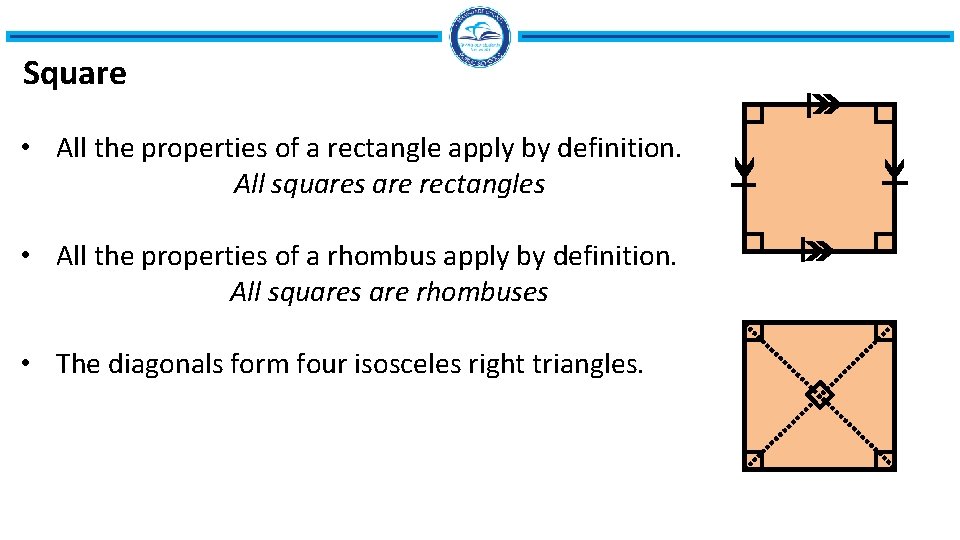
Square • All the properties of a rectangle apply by definition. All squares are rectangles • All the properties of a rhombus apply by definition. All squares are rhombuses • The diagonals form four isosceles right triangles.

Coordinate Geometry Proofs Slope: We use slope to show parallel lines and perpendicular lines. Parallel Lines have the same slope Perpendicular Lines have negative reciprocal slopes. Distance: We use distance to show line segments are congruent. Midpoint: We use midpoint to show that lines bisect each other. Lines with the same midpoint bisect each other.

Proving a triangle is a Right Triangle Method 1: Show two sides of the triangle are perpendicular by demonstrating their slopes are negative reciprocals. Method 2: Calculate the length of all three sides and then test the Pythagorean’s theorem to show the three lengths make the Pythagorean’s theorem true.

Proving a Quadrilateral is a Parallelogram Method 1: Show that the diagonals bisect each other by showing the midpoints of the diagonals are the same Method 2: Show both pairs of opposite sides are parallel by showing they have equal slopes. If the slope of two pairs of opposite sides are the same then the opposite sides are parallel, therefore the quadrilateral is a parallelogram Method 3: Show both pairs of opposite sides are equal by using distance. If two pairs of opposite sides are equal in length then the quadrilateral is a parallelogram Method 4: Show one pair of sides is both parallel and equal.

Proving a Quadrilateral is a Rectangle Method 1: Show that it has a right angle by using slope. If the slopes of two consecutive sides are opposite reciprocals then consecutive sides are perpendicular and form right angles, therefore the parallelogram is a rectangle. Method 2: Show that the diagonals are congruent. If the diagonals are congruent than the parallelogram is a rectangle.

Proving a Quadrilateral is a Rhombus Method 1: Prove that the diagonals are perpendicular. If the diagonals of a quadrilateral are perpendicular bisectors of each other, then it is a rhombus. Method 2: Show that the diagonals are congruent. If the diagonals are congruent than the parallelogram is a rectangle.

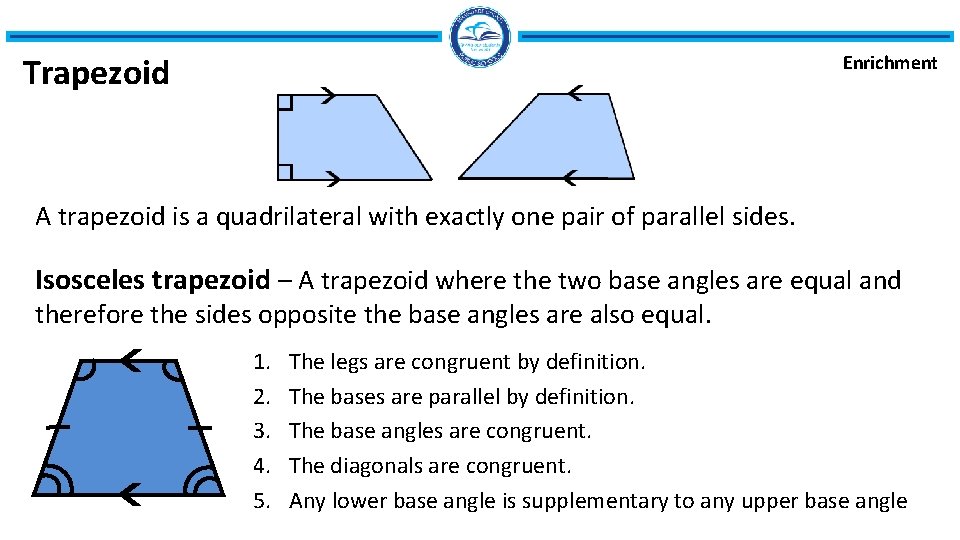
Trapezoid Enrichment A trapezoid is a quadrilateral with exactly one pair of parallel sides. Isosceles trapezoid – A trapezoid where the two base angles are equal and therefore the sides opposite the base angles are also equal. 1. 2. 3. 4. 5. The legs are congruent by definition. The bases are parallel by definition. The base angles are congruent. The diagonals are congruent. Any lower base angle is supplementary to any upper base angle